浙教版九年级上册3.3 圆心角（1）

课件31张PPT。3.3 圆心角（1）义务教育课程标准实验教科　
浙江版《数学》九年级上册
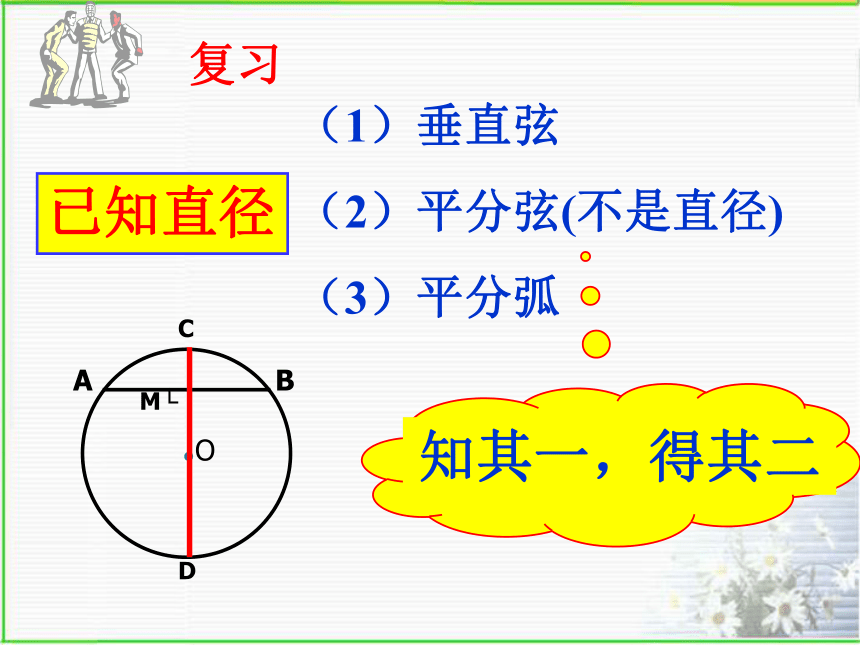
复习（1）垂直弦
（2）平分弦(不是直径)
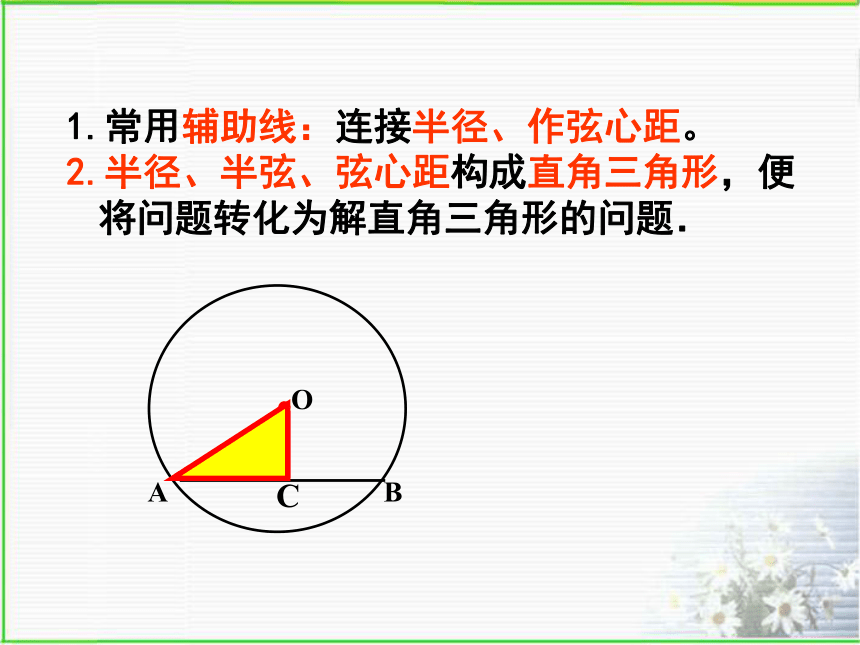
（3）平分弧已知直径知其一，得其二常用辅助线：连接半径、作弦心距。
半径、半弦、弦心距构成直角三角形，便将问题转化为解直角三角形的问题． OACB 已知圆O的半径为13cm,AB∥CD,AB=24cm,CD=10cm,
则AB与CD距离是__________cm 过点O作弦AB的垂线, 垂足
为M,AB 顶点在圆心的角,叫圆心角，
如 , 所对的弦为AB；图1 则垂线段OM的长度,即圆
心到弦的距离，叫弦心距 , 图1
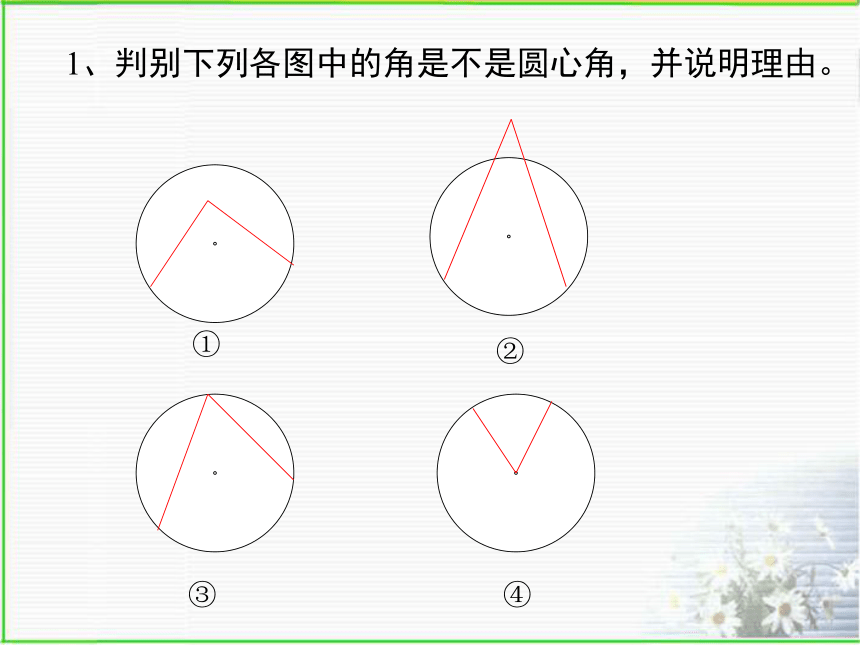
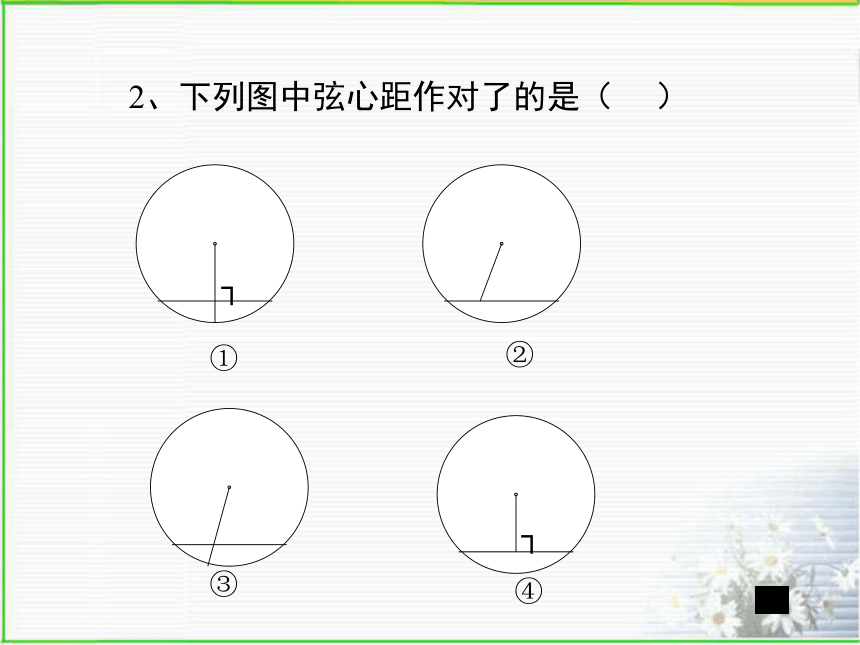
中，OM为AB弦的弦心距。M1、判别下列各图中的角是不是圆心角，并说明理由。①②③④2、下列图中弦心距作对了的是（ ）┐┐①②③④探索
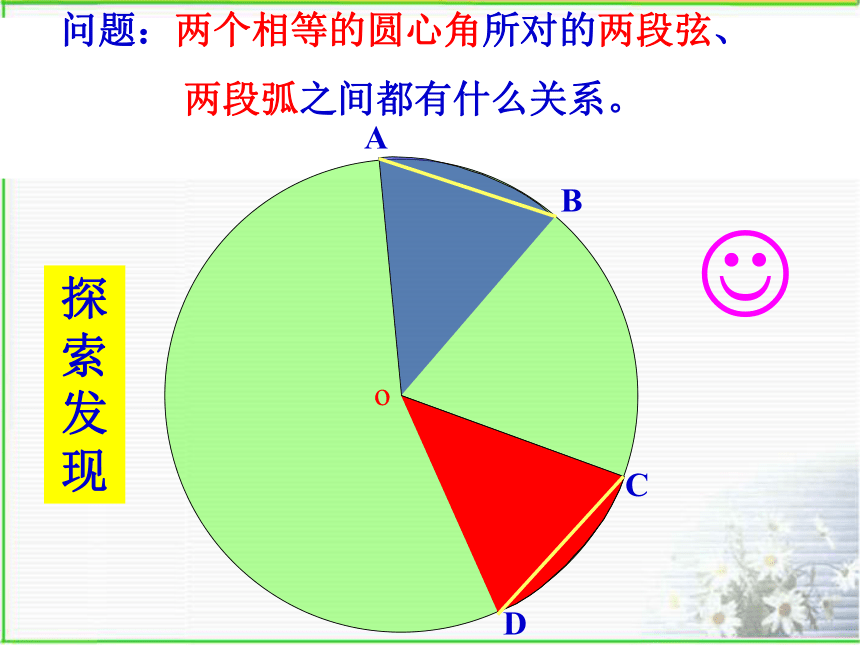
发现CDo?AB问题：两个相等的圆心角所对的两段弦、
两段弧之间都有什么关系。o?ABCD问题：两个相等的圆心角所对的两段弦、
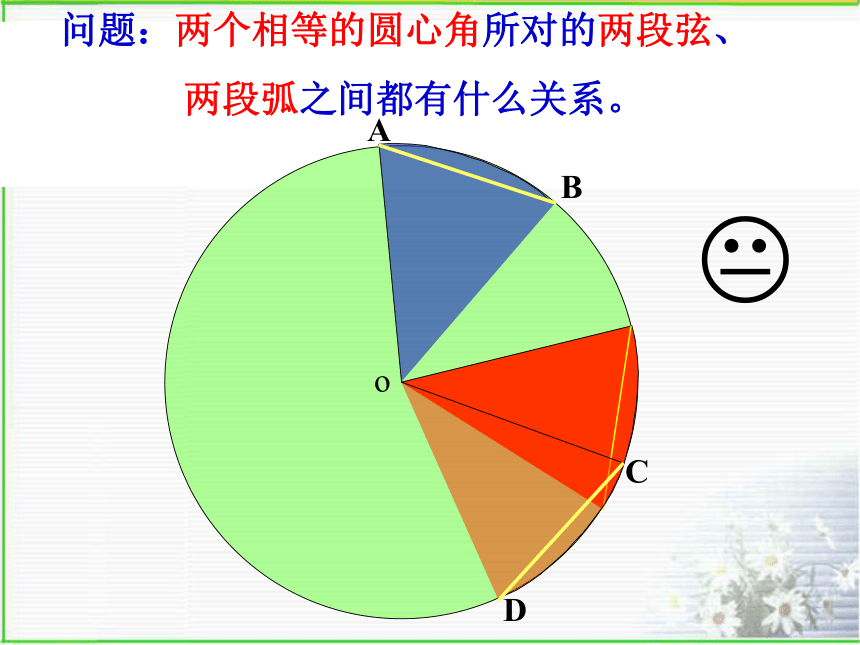
两段弧之间都有什么关系。o?ABCD问题：两个相等的圆心角所对的两段弦、
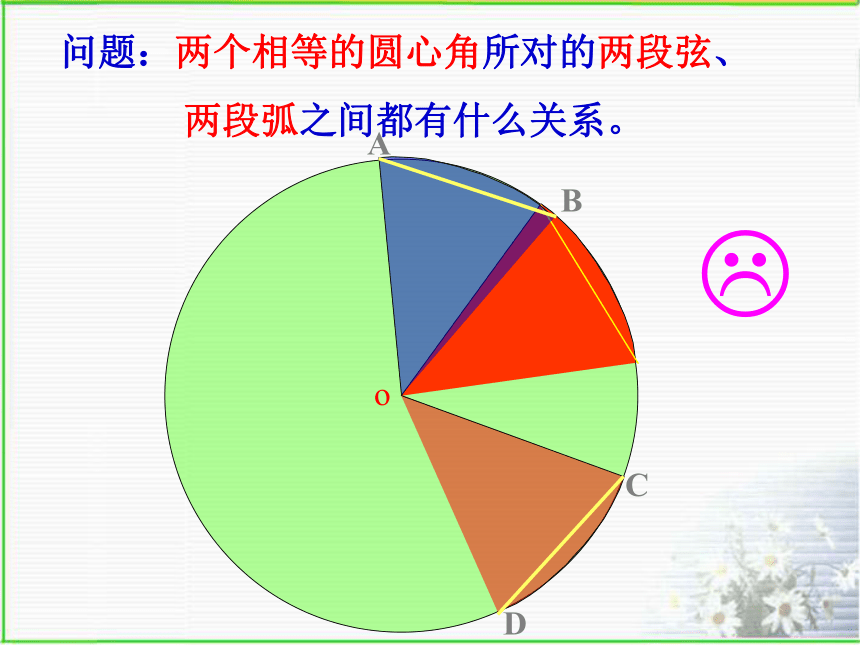
两段弧之间都有什么关系。o?ABCD问题：两个相等的圆心角所对的两段弦、
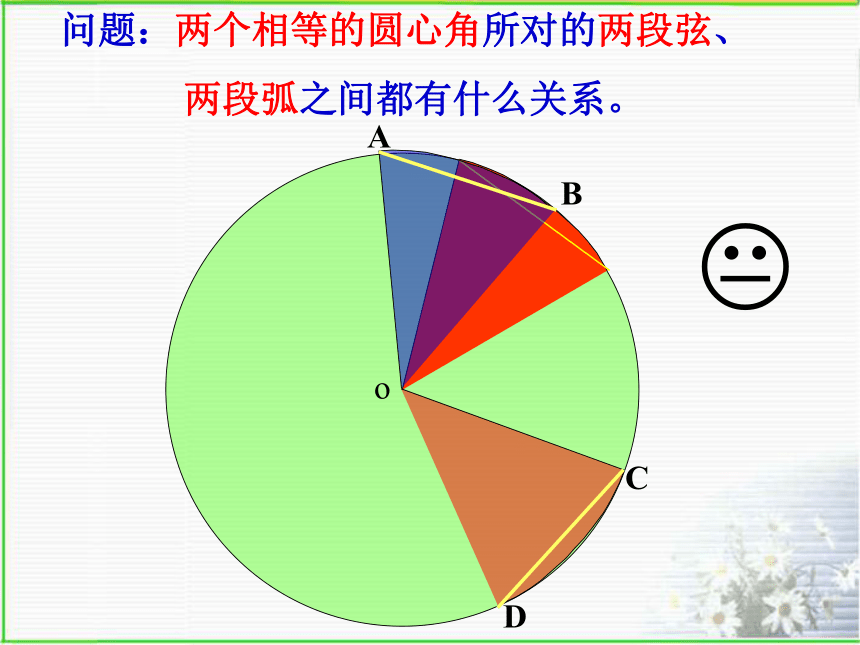
两段弧之间都有什么关系。o?ABCD问题：两个相等的圆心角所对的两段弦、
两段弧之间都有什么关系。圆心角定理：　相等的圆心角：所对的弧相等，
　　　　　　　　所对的弦相等　　　　　　　　　　　　所对弦的弦心距相等在同圆或等圆中，∵∠AOB=∠COD
∴ AB=CD AB=CDOE=OF已知：如图， ∠ 1= ∠ 2，求证：AC=BD证明：∵ ∠ 1= ∠ 2例1：O课本P71作业题2例2:用直尺和圆规把⊙Ｏ四等分．　 Ｏ 作法：１、作⊙Ｏ的直径ＡＢ。
　　　　２、过点Ｏ作ＣＤ⊥ＡＢ，交⊙Ｏ于
　　 点Ｃ和点Ｄ。
　　 点Ａ，Ｂ，Ｃ，Ｄ就把⊙Ｏ四等分
　　　　　课本P70探究活动我们把1o的圆心角所对的弧叫做1o的弧.这样,1o的圆心角对着1o的弧,
1o的弧对着1o的圆心角.
n o的圆心角对着no的弧,
n o的弧对着no的圆心角. 性质：:弧的度数和它所对圆心角的度数相等.AOB性质：:弧既有度数又有长度.注意：弧既有度数又有长度!OO问题：度数相等的弧相等吗?
长度相等的弧相等吗?练一练（2）：1.如图一，已知∠AOC=135。则CB的度数为—图（一） 2：如图，等边三角形ABC内接于⊙O,连结OA,OB,OC。(1)∠AOB、∠COB、∠AOC的度数分别为__________拓展创新ABCDOE推论１ : 在同圆或等圆中，相等的弧所对的圆心角相等，所对的弦相等，所对的弦的弦心距相等。推论2 : 在同圆或等圆中，相等的弦所对的圆心角相等，所对的弧相等，弦的弦心距相等。推论 3 : 在同圆或等圆中，相等的弦心距对应弦相等,弦所对的圆心角相等，所对的弧相等。一般地，圆有下面的性质
在同圆或等圆中，如果两个圆心角、两条弧、两条弦、两个弦心距中有一组量相等，那么它们所对应的其余的各组量都相等。⑴∠AOB=∠COD⑵AB=CD⑶OE=OF例1：已知：如图, AB、DE是⊙O的两条直径，C是⊙O上一点，且AD=CE。求证：BE=CE⌒⌒例2：已知：如图,弦AB=CD，M、N是弦AB、CD的中点。求证：∠AMN=∠CNM通过本节的学习，你对圆有哪些新的认识？回顾与小结例2：如图，等边三角形ABC内接于⊙O,连结OA,OB,OC。例3：如图, AB、CD是⊙O的两条直径。(1)顺次连结点A、C、B、D，所得的四边形是什么特殊四边形？为什么？(2)若直径为10cm，∠AOB=1200，求四边形ACBD的周长和面积。例3：如图, AB、CD是⊙O的两条直径。(3)四边形ACBD有可能为正方形吗？若有可能,当AB、CD有何位置关系时，四边形ACBD为正方形？为什么？