5.1多边形（3）

课件30张PPT。 八年级下册
5.1 多边形（3）
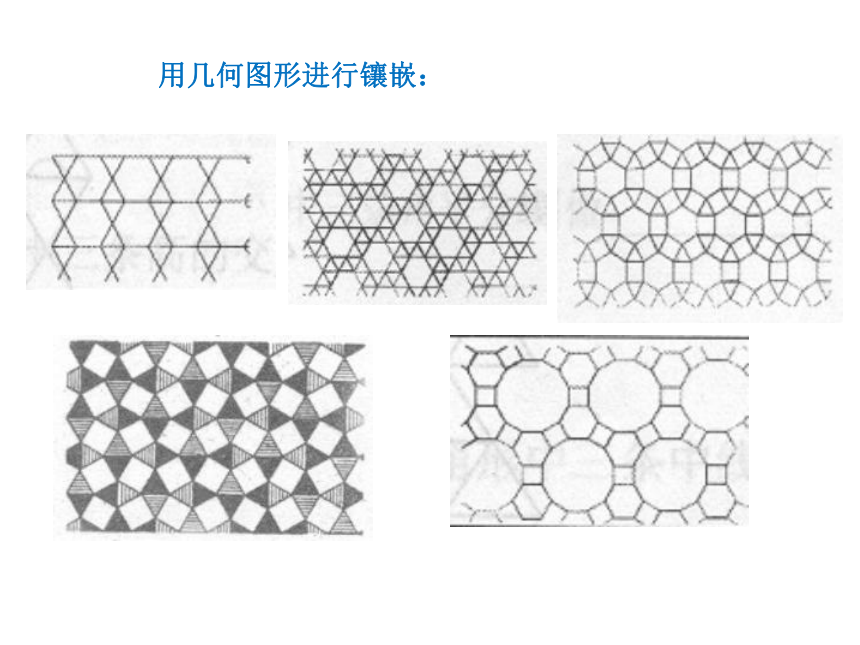
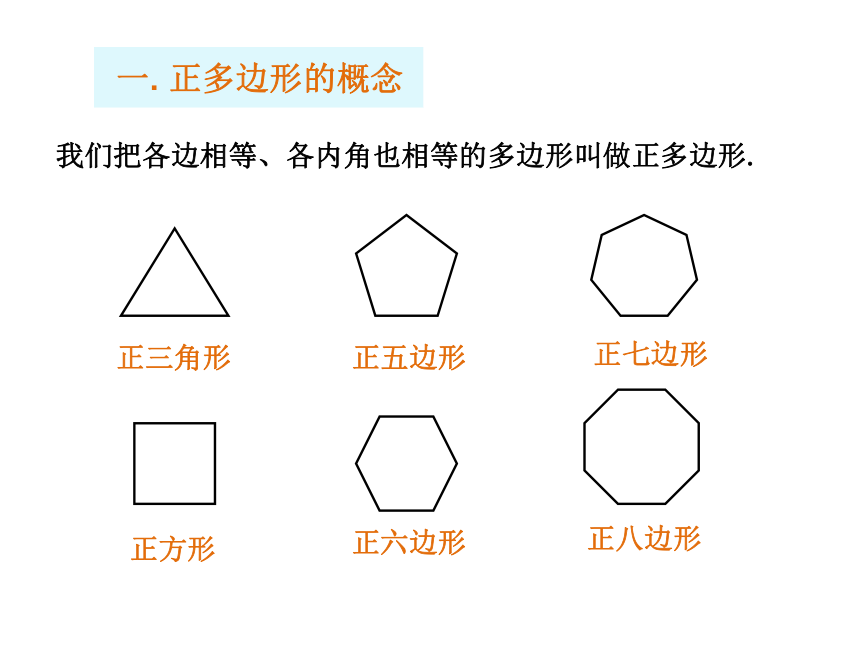
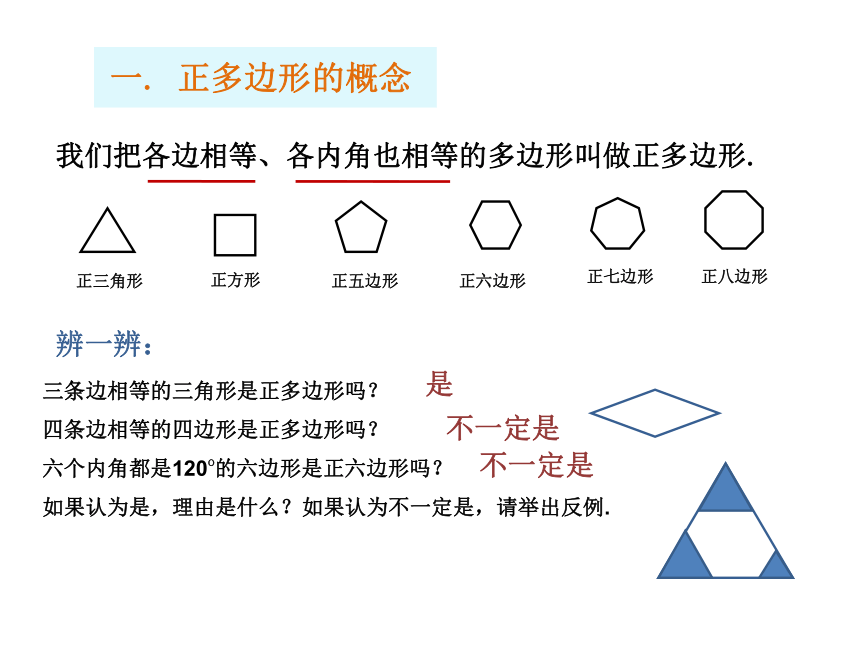
___ 用正多边形镶嵌平面 用形状、大小完全相同的一种或几种平面图形进行拼接，彼此之间不留空隙、不重叠地铺成一片，这就是图形的密铺，又称图形的镶嵌. 用几何图形进行镶嵌： 著名图形艺术家埃舍尔的镶嵌作品： 外国六年级小学生的作品：一. 正多边形的概念我们把各边相等、各内角也相等的多边形叫做正多边形.正三角形正方形正五边形正六边形正七边形正八边形一. 正多边形的概念我们把各边相等、各内角也相等的多边形叫做正多边形.正三角形正方形正五边形正六边形正七边形正八边形辨一辨：三条边相等的三角形是正多边形吗？
四条边相等的四边形是正多边形吗？
六个内角都是120o的六边形是正六边形吗？
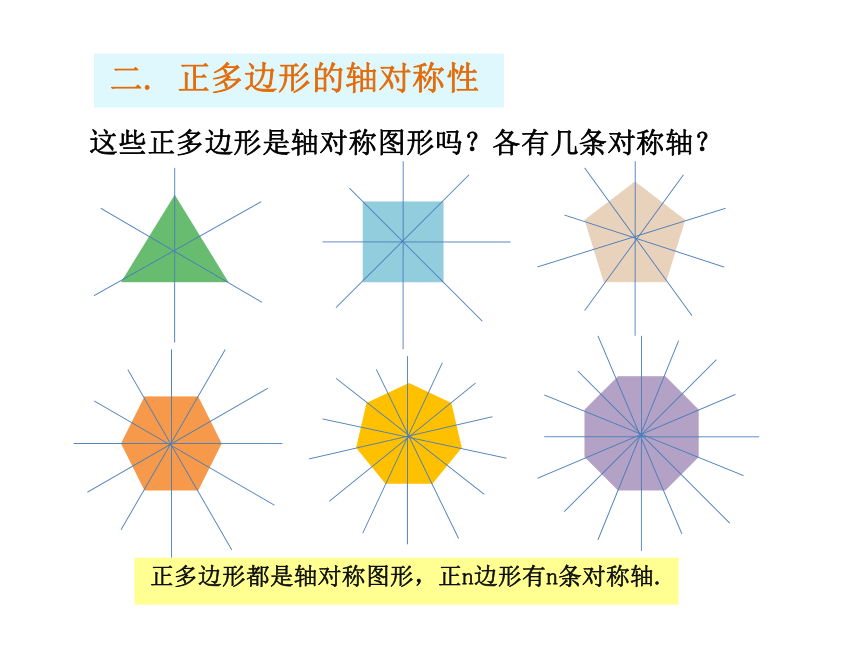
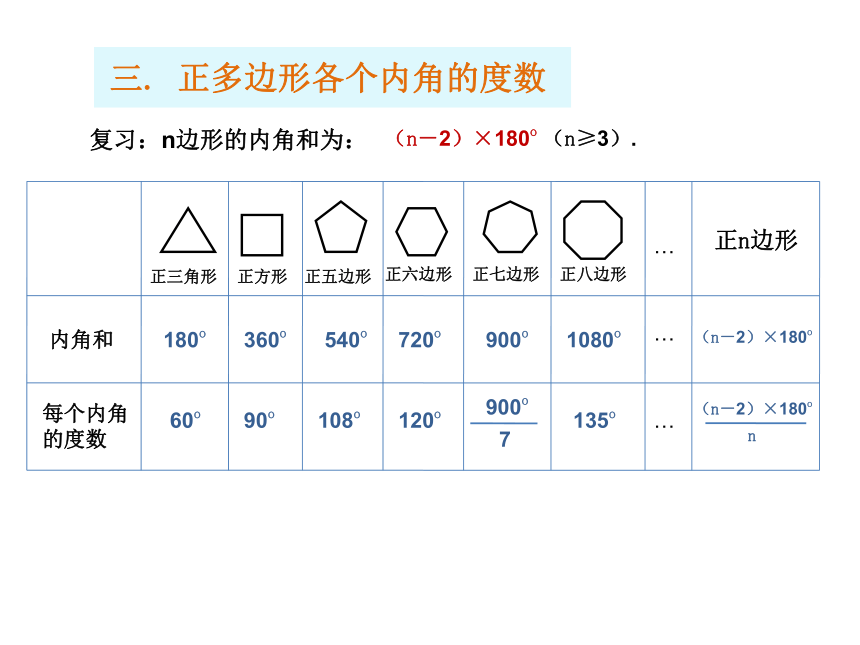
如果认为是，理由是什么？如果认为不一定是，请举出反例.是不一定是不一定是二. 正多边形的轴对称性这些正多边形是轴对称图形吗？各有几条对称轴？正多边形都是轴对称图形，正n边形有n条对称轴.三. 正多边形各个内角的度数复习：n边形的内角和为：正三角形正方形正五边形正六边形正七边形正八边形内角和每个内角的度数正n边形………180o360o540o720o900o1080o（n－2）×180o 60o90o108o120o900o135o7（n－2）×180o n（n－2）×180o （n≥3）. 四. 用正多边形镶嵌平面合作学习 1：哪些正多边形可以单独镶嵌平面
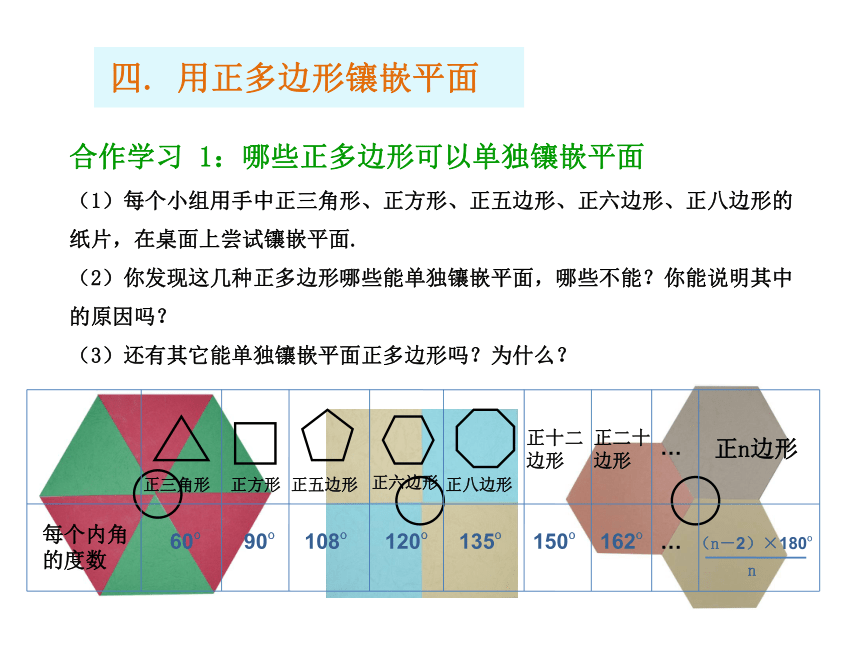
（1）每个小组用手中正三角形、正方形、正五边形、正六边形、正八边形的纸片，在桌面上尝试镶嵌平面.
（2）你发现这几种正多边形哪些能单独镶嵌平面，哪些不能？你能说明其中的原因吗？
（3）还有其它能单独镶嵌平面正多边形吗？为什么？四. 用正多边形镶嵌平面合作学习 1：哪些正多边形可以单独镶嵌平面
（1）每个小组用手中正三角形、正方形、正五边形、正六边形、正八边形的纸片，在桌面上尝试镶嵌平面.
（2）你发现这几种正多边形哪些能单独镶嵌平面，哪些不能？你能说明其中的原因吗？
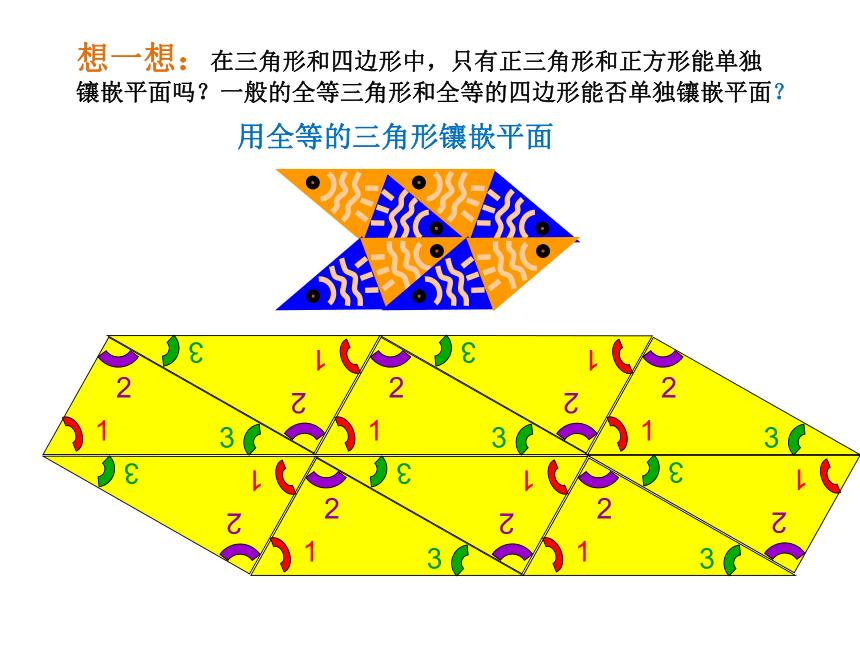
（3）还有其它能单独镶嵌平面正多边形吗？为什么？想一想：在三角形和四边形中，只有正三角形和正方形能单独镶嵌平面吗？一般的全等三角形和全等的四边形能否单独镶嵌平面？用全等的三角形镶嵌平面用全等的四边形镶嵌平面想一想：在三角形和四边形中，只有正三角形和正方形能单独镶嵌平面吗？一般的全等三角形和全等的四边形能否单独镶嵌平面？生活中有时也用几种多边形组合起来镶嵌平面四. 用正多边形镶嵌平面例：如图用边长相等的正八边形和正方形镶嵌平面，请说明其中的数学原理.解：数学原理是：
正八边形的内角为135o，
正方形的内角为90o，
每个拼接点处由2个正八边形的内角和1个正方形的内角拼成，满足：
135o×2＋90o×1=360o，
又因为它们的边长相等，所以刚好能镶嵌平面.合作学习 2：请你尝试用两种或两种以上的正多边形镶嵌平面，拼一拼或算一算，并说明其中的数学原理.四. 用正多边形镶嵌平面每个拼接点处由2个正八边形的内角和1个正方形的内角拼成，满足
135o×2＋90o×1=360o☆方案①方案③方案④☆方案②☆方案⑤方案⑥方案⑦ …正三角形和正方形…请你欣赏正三角形和正六边形…请你欣赏正三角形和正十二边形…请你欣赏正五边形和正十边形…请你欣赏正三角形、正方形和正六边形…请你欣赏正方形、正六边形和正十二边形…请你欣赏正方形、正五边形和正二十边形…请你欣赏总结规律设两种正多边形的内角分别为α和β，如果它们能镶嵌平面，则必定存在正整数 m 和 n，使得：α×m+β×n = 360o举例：正三角形和正六边形之所以能镶嵌平面，是因为我们找到了两个正整数 m 和 n ，使得：
60 m + 120 n = 360.其中 m=4，n=1 或 m=2, n=2.正五边形和正十边形课堂小结你学到了用哪些图形可以镶嵌平面？1. 能单独镶嵌平面的正多边形只有正三角形、正方形、正六边形3种.2. 全等的三角形和全等的四边形也能单独镶嵌平面.用几种正多边形组合镶嵌平面的方案非常多.
主要看围绕一个共同的顶点（即拼接点）的几种正多边形的内角之和是否为360o.但有时能否镶嵌整个平面还与具体边数有关。破解图形设计的密码请看镶嵌图案设计的过程 两个图像的外部轮廓也是全等的，只是内部绘制了不同的图形而已。课后作业完成作业本
自选几种正多边形设计一幅镶嵌图.感谢大家
再见！