3.2三角形的内切圆
图片预览


文档简介
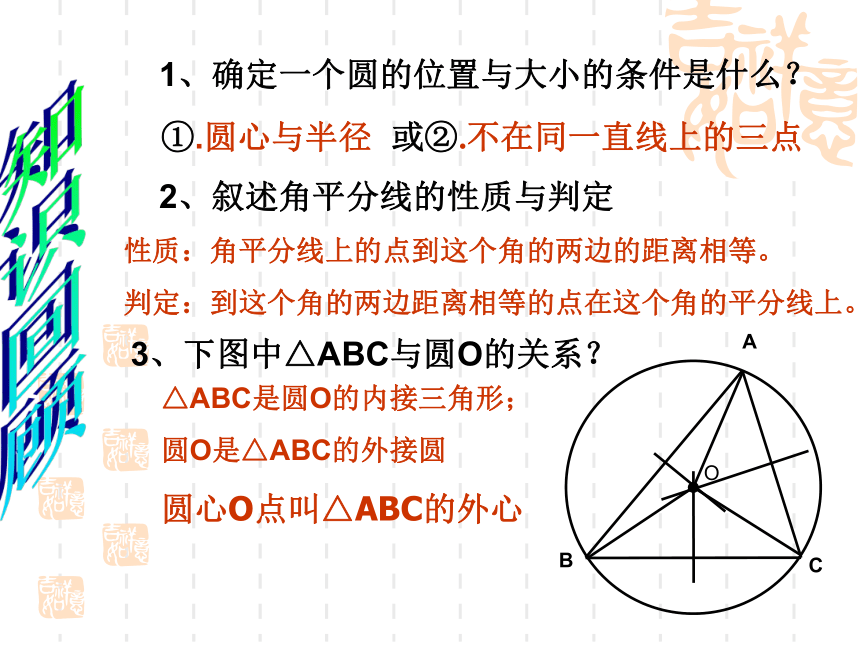
课件20张PPT。1、确定一个圆的位置与大小的条件是什么?①.圆心与半径2、叙述角平分线的性质与判定性质:角平分线上的点到这个角的两边的距离相等。
判定:到这个角的两边距离相等的点在这个角的平分线上。3、下图中△ABC与圆O的关系?△ABC是圆O的内接三角形;
圆O是△ABC的外接圆
圆心O点叫△ABC的外心知识回顾或②.不在同一直线上的三点ABCO 李明在一家木料厂上班,工作之余想对厂里的三角形废料进行加工:裁下一块圆形用料,且使圆的面积最大。
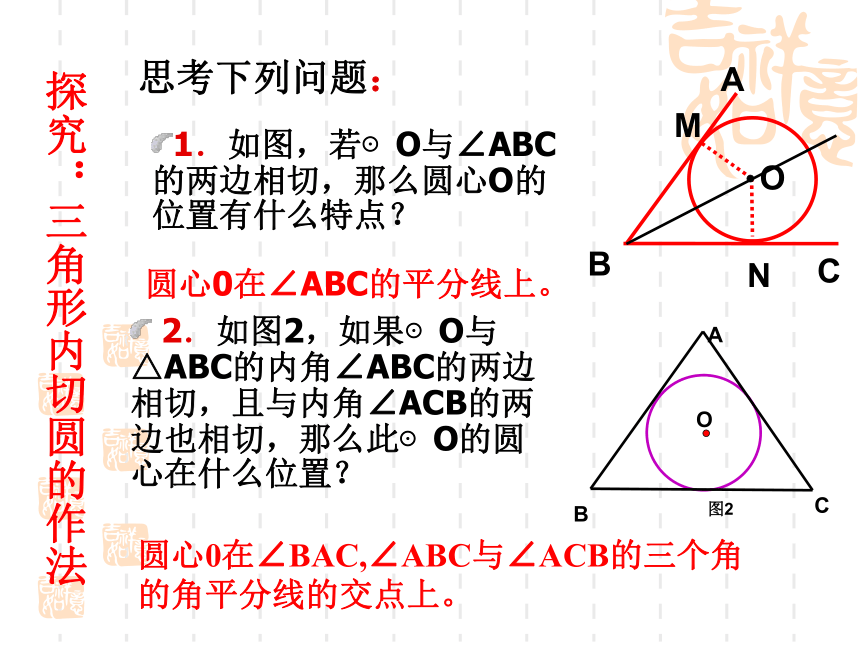
下图是他的几种设计,请同学们帮他确定一下。思考ABC三角形的内切圆Or课 题思考下列问题:1.如图,若⊙O与∠ABC的两边相切,那么圆心O的位置有什么特点?圆心0在∠ABC的平分线上。?2.如图2,如果⊙O与△ABC的内角∠ABC的两边相切,且与内角∠ACB的两边也相切,那么此⊙O的圆心在什么位置?圆心0在∠BAC,∠ABC与∠ACB的三个角的角平分线的交点上。 OMABCN探究:三角形内切圆的作法3.如何确定一个与三角形 三边都相切的圆的圆心位置 与半径的长? 4.你能作出几个与一个三角形的三边都相切的圆么?内切圆圆心能否在三角形外部? 作出三个内角的平分线,三条内角
平分线相交于一点,这点就是符合
条件的圆心,过圆心作一边的垂线,
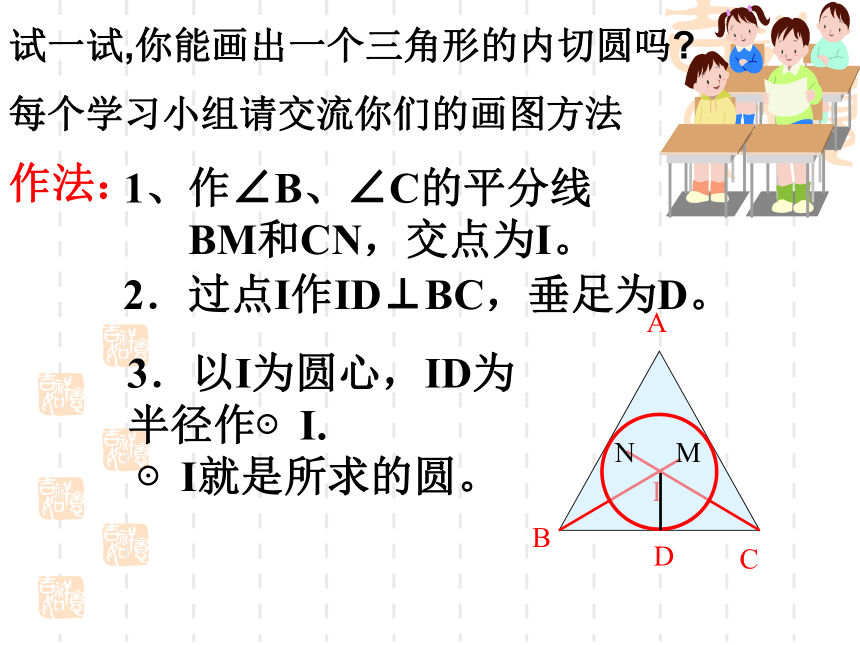
垂线段的长是符合条件的半径。 只能作一个,圆心也只能在三角形内部,因为三角形的三条内角平分线在三角形内部,且相交只有一个交点。 IFCABED作法: ABC1、作∠B、∠C的平分线
BM和CN,交点为I。 I2.过点I作ID⊥BC,垂足为D。 3.以I为圆心,ID为
半径作⊙I.
⊙I就是所求的圆。 MN试一试,你能画出一个三角形的内切圆吗?
每个学习小组请交流你们的画图方法2、内心性质:
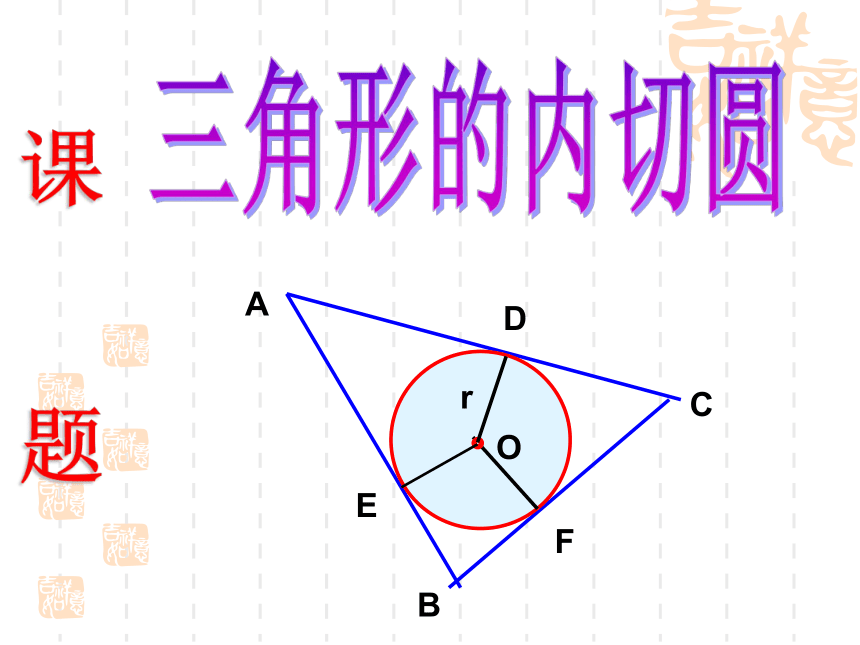
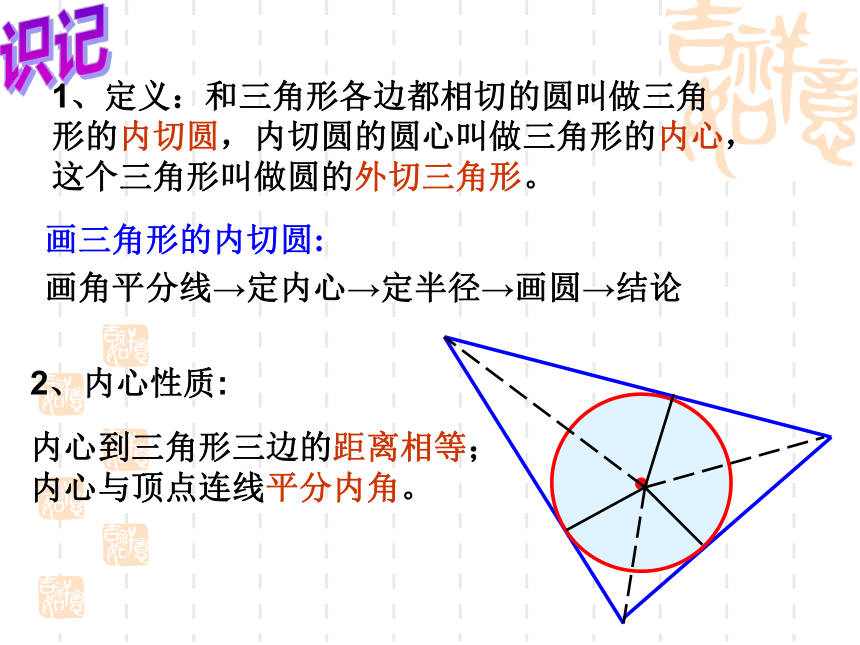
1、定义:和三角形各边都相切的圆叫做三角
形的内切圆,内切圆的圆心叫做三角形的内心,
这个三角形叫做圆的外切三角形。内心到三角形三边的距离相等;
内心与顶点连线平分内角。画三角形的内切圆:
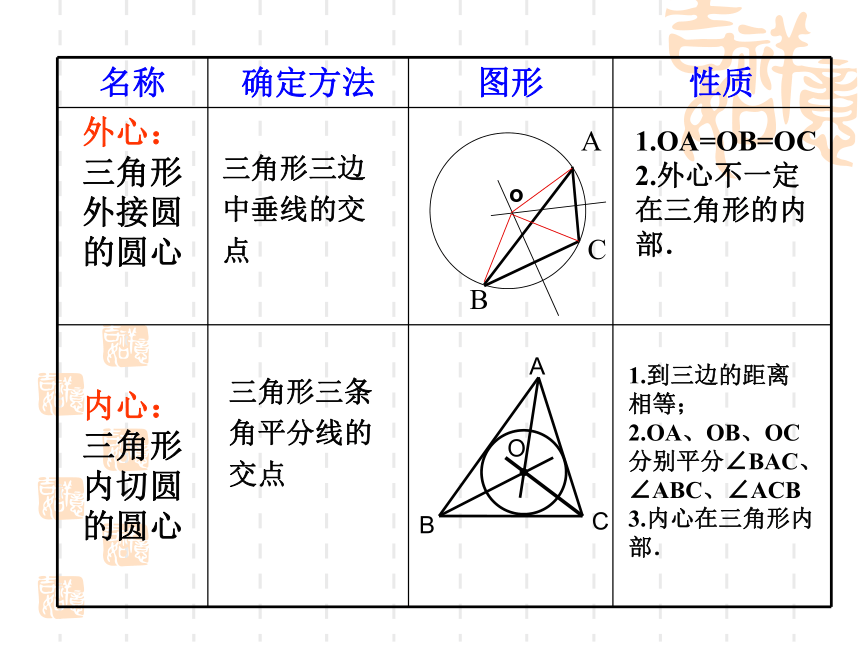
画角平分线→定内心→定半径→画圆→结论识记三角形三边
中垂线的交
点1.OA=OB=OC
2.外心不一定在三角形的内部.三角形三条
角平分线的
交点1.到三边的距离
相等;
2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB
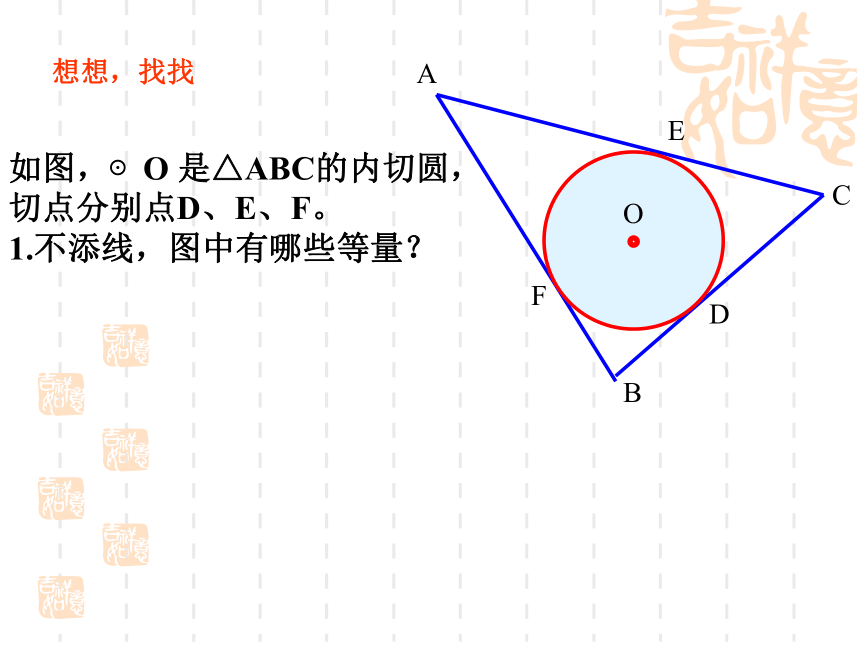
3.内心在三角形内部.oABC想想,找找如图,⊙O 是△ABC的内切圆,
切点分别点D、E、F。
1.不添线,图中有哪些等量?想想,找找如图,⊙O 是△ABC的内切圆,
切点分别点D、E、F。
1.不添线,图中有哪些等量?2.连结OA、OB、OC,你又有
何发现?想想,找找如图,⊙O 是△ABC的内切圆,
切点分别点D、E、F。
1.不添线,图中有哪些等量?2.连结OA、OB、OC,你又有
何发现?3.连结OD、OE、OF,你还有新发现吗?题1:
如图,在△ABC中,点O是内心,∠ABC=50°,∠ACB=70°,求∠BOC的度数。想想,做做变式1:在△ABC中,点O是内心,
∠BAC=50°,求∠BOC的度数。变式2:在△ABC中,点O是内心,
∠BOC=120°,求∠BAC的度数。题2:
求边长为6cm的等边三角形的内切圆半径r与外接圆半径R。老师提示:
先画草图,由等腰三角形底边上的中垂
线与顶角平分线重合的性质知,等边三角形
的内切圆与外接圆是两个同心圆。变式:
求边长为a的等边三角形的内切圆
半径r与外接圆半径R的比。想想,做做题3:
设△ABC的面积为S,周长为L, △ABC内切圆
的半径为r,你能
得到S= Lr吗?想想:
我们学过哪些求三角形面积的公式?想想,做做题4:如图,已知⊙O 是△ABC的内切圆,切点分别点D、E、F,设△ABC周长为L。
求证:AE+BC= L想想,做做B想一想:
常用辅助线及切线的性质圆内接平行四边形是矩形圆外切平行四边形是_______F延伸与拓展菱形EGHABCOcDEr如:直角三角形的两直角边分别是5cm,12cm 则其内切圆的半径为______。 补充题:
如图,直角三角形的两直角边分别是a,b,斜边为c 则其内切圆的半径r为:
(以含a、b、c的代数式表示r)2cm探究活动以某三角形的内心为圆心,
作一个圆使它与这个三角形
的某一条边(或所在的直线)有两个交点,那么这个圆与其他两边(或所在的直线)有怎样的位置关系?仔细观察图形,你还能发现什么规律?再作几个三角形试一试,是否有同样的规律?请说明理由.OABCFEDGHI我有哪些收获?
---与大家共分享!学 而 不 思 则 罔回头一看,我想说…1.定义2.内心的性质4.初步应用3.画三角形的内切圆知 识 的 应 用
判定:到这个角的两边距离相等的点在这个角的平分线上。3、下图中△ABC与圆O的关系?△ABC是圆O的内接三角形;
圆O是△ABC的外接圆
圆心O点叫△ABC的外心知识回顾或②.不在同一直线上的三点ABCO 李明在一家木料厂上班,工作之余想对厂里的三角形废料进行加工:裁下一块圆形用料,且使圆的面积最大。
下图是他的几种设计,请同学们帮他确定一下。思考ABC三角形的内切圆Or课 题思考下列问题:1.如图,若⊙O与∠ABC的两边相切,那么圆心O的位置有什么特点?圆心0在∠ABC的平分线上。?2.如图2,如果⊙O与△ABC的内角∠ABC的两边相切,且与内角∠ACB的两边也相切,那么此⊙O的圆心在什么位置?圆心0在∠BAC,∠ABC与∠ACB的三个角的角平分线的交点上。 OMABCN探究:三角形内切圆的作法3.如何确定一个与三角形 三边都相切的圆的圆心位置 与半径的长? 4.你能作出几个与一个三角形的三边都相切的圆么?内切圆圆心能否在三角形外部? 作出三个内角的平分线,三条内角
平分线相交于一点,这点就是符合
条件的圆心,过圆心作一边的垂线,
垂线段的长是符合条件的半径。 只能作一个,圆心也只能在三角形内部,因为三角形的三条内角平分线在三角形内部,且相交只有一个交点。 IFCABED作法: ABC1、作∠B、∠C的平分线
BM和CN,交点为I。 I2.过点I作ID⊥BC,垂足为D。 3.以I为圆心,ID为
半径作⊙I.
⊙I就是所求的圆。 MN试一试,你能画出一个三角形的内切圆吗?
每个学习小组请交流你们的画图方法2、内心性质:
1、定义:和三角形各边都相切的圆叫做三角
形的内切圆,内切圆的圆心叫做三角形的内心,
这个三角形叫做圆的外切三角形。内心到三角形三边的距离相等;
内心与顶点连线平分内角。画三角形的内切圆:
画角平分线→定内心→定半径→画圆→结论识记三角形三边
中垂线的交
点1.OA=OB=OC
2.外心不一定在三角形的内部.三角形三条
角平分线的
交点1.到三边的距离
相等;
2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB
3.内心在三角形内部.oABC想想,找找如图,⊙O 是△ABC的内切圆,
切点分别点D、E、F。
1.不添线,图中有哪些等量?想想,找找如图,⊙O 是△ABC的内切圆,
切点分别点D、E、F。
1.不添线,图中有哪些等量?2.连结OA、OB、OC,你又有
何发现?想想,找找如图,⊙O 是△ABC的内切圆,
切点分别点D、E、F。
1.不添线,图中有哪些等量?2.连结OA、OB、OC,你又有
何发现?3.连结OD、OE、OF,你还有新发现吗?题1:
如图,在△ABC中,点O是内心,∠ABC=50°,∠ACB=70°,求∠BOC的度数。想想,做做变式1:在△ABC中,点O是内心,
∠BAC=50°,求∠BOC的度数。变式2:在△ABC中,点O是内心,
∠BOC=120°,求∠BAC的度数。题2:
求边长为6cm的等边三角形的内切圆半径r与外接圆半径R。老师提示:
先画草图,由等腰三角形底边上的中垂
线与顶角平分线重合的性质知,等边三角形
的内切圆与外接圆是两个同心圆。变式:
求边长为a的等边三角形的内切圆
半径r与外接圆半径R的比。想想,做做题3:
设△ABC的面积为S,周长为L, △ABC内切圆
的半径为r,你能
得到S= Lr吗?想想:
我们学过哪些求三角形面积的公式?想想,做做题4:如图,已知⊙O 是△ABC的内切圆,切点分别点D、E、F,设△ABC周长为L。
求证:AE+BC= L想想,做做B想一想:
常用辅助线及切线的性质圆内接平行四边形是矩形圆外切平行四边形是_______F延伸与拓展菱形EGHABCOcDEr如:直角三角形的两直角边分别是5cm,12cm 则其内切圆的半径为______。 补充题:
如图,直角三角形的两直角边分别是a,b,斜边为c 则其内切圆的半径r为:
(以含a、b、c的代数式表示r)2cm探究活动以某三角形的内心为圆心,
作一个圆使它与这个三角形
的某一条边(或所在的直线)有两个交点,那么这个圆与其他两边(或所在的直线)有怎样的位置关系?仔细观察图形,你还能发现什么规律?再作几个三角形试一试,是否有同样的规律?请说明理由.OABCFEDGHI我有哪些收获?
---与大家共分享!学 而 不 思 则 罔回头一看,我想说…1.定义2.内心的性质4.初步应用3.画三角形的内切圆知 识 的 应 用
