2021-2022学年初中数学浙教版(2012)九年级下册第2章2.1直线与圆的位置关系 小节练习(word版含答案)
文档属性
| 名称 | 2021-2022学年初中数学浙教版(2012)九年级下册第2章2.1直线与圆的位置关系 小节练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 261.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-04 07:13:40 | ||
图片预览


文档简介
第2章2.1直线与圆的位置关系
一、选择题(共15题)
已知 的半径为 ,圆心 到直线 的距离为 ,过 上任一点 作 的切线,切点为 ,则线段 长度的最小值为
A. B. C. D.
以坐标原点 为圆心,作半径为 的圆,若直线 与 相交,则 的取值范围是
A. B.
C. D.
如图所示,某石油公司计划在三条公路围成的一块平地上建一个加油站,综合各种因素,要求这个加油站到三条公路的距离相等,则应建在
A. 的三条内角平分线的交点处
B. 的三条高线的交点处
C. 的三边的垂直平分线的交点处
D. 的三条中线的交点处
已知 的半径 ,直线 与 的圆心的距离 ,则直线 与圆的位置关系是
A.相离 B.相交 C.相切 D.无法确定
在平面直角坐标系中,以点 为圆心, 为半径的圆必定
A.与 轴相切 B.与 轴相离 C.与 轴相切 D.与 轴相离
如图所示,从 外一点 引 的两条切线 、 ,切点分别为 、 .如果 ,,那么弦 的长是
A. B. C. D.
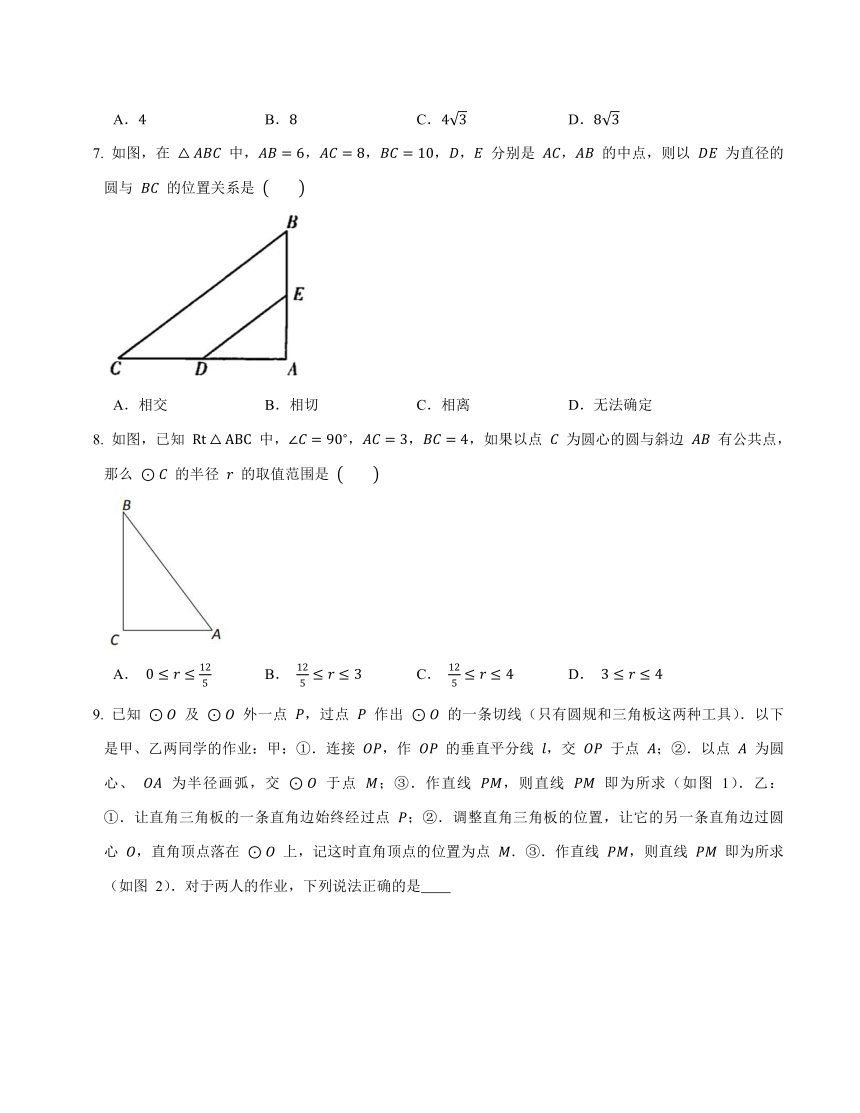
如图,在 中,,,,, 分别是 , 的中点,则以 为直径的圆与 的位置关系是
A.相交 B.相切 C.相离 D.无法确定
如图,已知 中,,,,如果以点 为圆心的圆与斜边 有公共点,那么 的半径 的取值范围是
A. B. C. D.
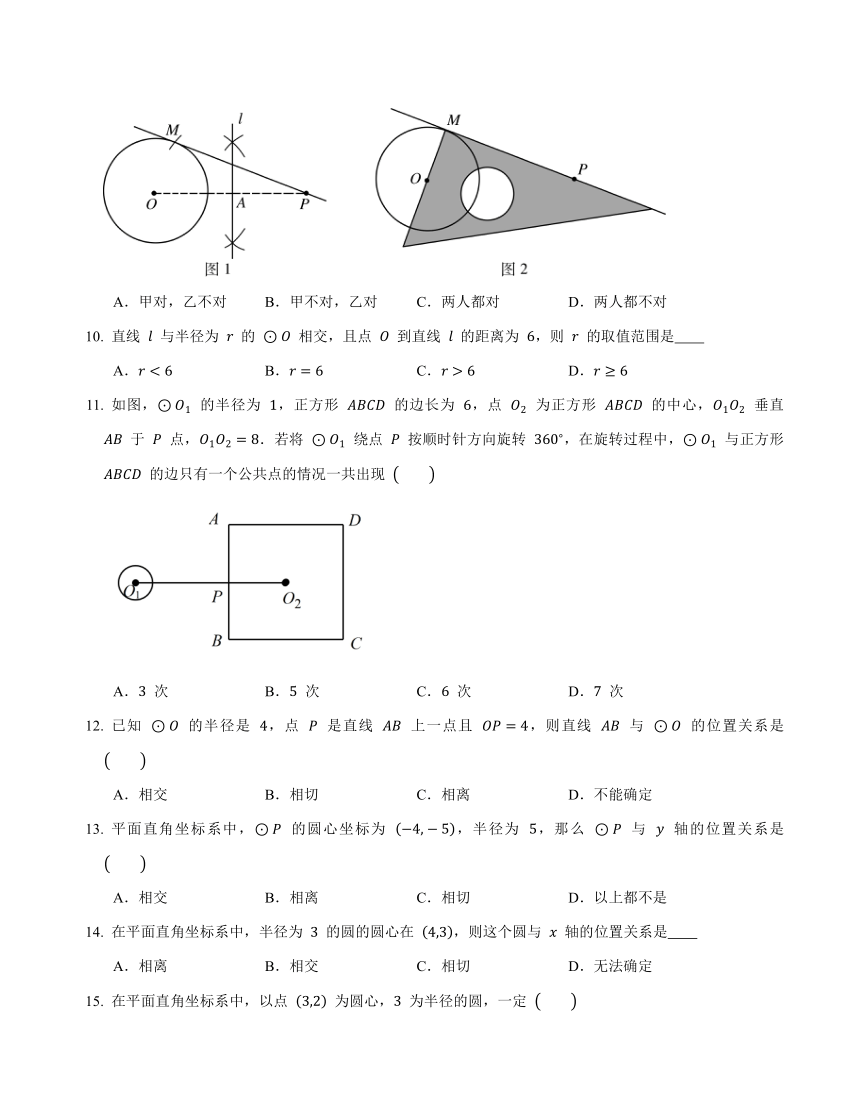
已知 及 外一点 ,过点 作出 的一条切线(只有圆规和三角板这两种工具).以下是甲、乙两同学的作业:甲:①.连接 ,作 的垂直平分线 ,交 于点 ;②.以点 为圆心、 为半径画弧,交 于点 ;③.作直线 ,则直线 即为所求(如图 1).乙:①.让直角三角板的一条直角边始终经过点 ;②.调整直角三角板的位置,让它的另一条直角边过圆心 ,直角顶点落在 上,记这时直角顶点的位置为点 .③.作直线 ,则直线 即为所求(如图 2).对于两人的作业,下列说法正确的是
A.甲对,乙不对 B.甲不对,乙对 C.两人都对 D.两人都不对
直线 与半径为 的 相交,且点 到直线 的距离为 ,则 的取值范围是
A. B. C. D.
如图, 的半径为 ,正方形 的边长为 ,点 为正方形 的中心, 垂直 于 点,.若将 绕点 按顺时针方向旋转 ,在旋转过程中, 与正方形 的边只有一个公共点的情况一共出现
A. 次 B. 次 C. 次 D. 次
已知 的半径是 ,点 是直线 上一点且 ,则直线 与 的位置关系是
A.相交 B.相切 C.相离 D.不能确定
平面直角坐标系中, 的圆心坐标为 ,半径为 ,那么 与 轴的位置关系是
A.相交 B.相离 C.相切 D.以上都不是
在平面直角坐标系中,半径为 的圆的圆心在 ,则这个圆与 轴的位置关系是
A.相离 B.相交 C.相切 D.无法确定
在平面直角坐标系中,以点 为圆心, 为半径的圆,一定
A.与 轴相切,与 轴相切 B.与 轴相切,与 轴相交
C.与 轴相交,与 轴相切 D.与 轴相交,与 轴相交
二、填空题(共5题)
如图,线段 的长度为 , 所在直线上方存在点 ,使得 为等腰三角形,设 的面积为 .当 时,满足条件的点 恰有三个.
如图,正方形 的边长为 , 是 的中点, 是 边上的动点,连接 ,以点 为圆心, 长为半径作 .当 与正方形 的边相切时, 的长为 .
如图所示, 的一边 是 的直径,请你添加一个条件,使 是 的切线,你所添加的条件为 .
如图, 的半径为 , 是 延长线上一点,, 切 于 点,那么 的切线 的长为 .
以三角形的一边为直径的圆恰好与另一边相切,则此三角形是 三角形.
三、解答题(共5题)
如图,已知以 为圆心, 为半径的圆交 于点 .若 ,,,则 是 的切线吗?并说明理由.
如图,已知 的直径 与弦 互相垂直,垂足为点 . 的切线 与弦 的延长线相交于点 ,且 ,.
(1)求证:.
(2)求 的半径.
(3)求弦 的长.
下列说法正确吗?若不正确,请画图说明.
(1)垂直于圆的半径的直线一定是这个圆的切线.
(2)过圆的半径的外端的直线一定是这个圆的切线.
如图,点 在 上.
()过点 作 的切线 .
()作出与 垂直的 的切线.
如图所示,已知点 为正方形 对角线 上一点,以点 为圆心,以 长为半径的 与 相切于点 ,与 , 分别相交于点 ,.求证: 与 相切.
答案
1. C
2. D
3. A
4. B
5. A
6. B
7. A
8. C
9. C
10. C
11. B
12. D
13. A
14. C
15. C
16. 或
17. 或
18.
19.
20. 直角
21. 说明 .
22. (1) 是 的切线,
.
,
.
(2) 连接 ,
是直径,
.
,,
.
又 ,
.
的半径为 .
(3) ,,
.
.
又 ,
.
23. (1) 不正确.反例略.
(2) 不正确.反例略.
24. 略
25. 如图所示,连接 ,作 于点 .
因为 与 相切,所以 .
因为四边形 是正方形,
所以 平分 .
所以 .
又因为 ,
所以 与 相切.
一、选择题(共15题)
已知 的半径为 ,圆心 到直线 的距离为 ,过 上任一点 作 的切线,切点为 ,则线段 长度的最小值为
A. B. C. D.
以坐标原点 为圆心,作半径为 的圆,若直线 与 相交,则 的取值范围是
A. B.
C. D.
如图所示,某石油公司计划在三条公路围成的一块平地上建一个加油站,综合各种因素,要求这个加油站到三条公路的距离相等,则应建在
A. 的三条内角平分线的交点处
B. 的三条高线的交点处
C. 的三边的垂直平分线的交点处
D. 的三条中线的交点处
已知 的半径 ,直线 与 的圆心的距离 ,则直线 与圆的位置关系是
A.相离 B.相交 C.相切 D.无法确定
在平面直角坐标系中,以点 为圆心, 为半径的圆必定
A.与 轴相切 B.与 轴相离 C.与 轴相切 D.与 轴相离
如图所示,从 外一点 引 的两条切线 、 ,切点分别为 、 .如果 ,,那么弦 的长是
A. B. C. D.
如图,在 中,,,,, 分别是 , 的中点,则以 为直径的圆与 的位置关系是
A.相交 B.相切 C.相离 D.无法确定
如图,已知 中,,,,如果以点 为圆心的圆与斜边 有公共点,那么 的半径 的取值范围是
A. B. C. D.
已知 及 外一点 ,过点 作出 的一条切线(只有圆规和三角板这两种工具).以下是甲、乙两同学的作业:甲:①.连接 ,作 的垂直平分线 ,交 于点 ;②.以点 为圆心、 为半径画弧,交 于点 ;③.作直线 ,则直线 即为所求(如图 1).乙:①.让直角三角板的一条直角边始终经过点 ;②.调整直角三角板的位置,让它的另一条直角边过圆心 ,直角顶点落在 上,记这时直角顶点的位置为点 .③.作直线 ,则直线 即为所求(如图 2).对于两人的作业,下列说法正确的是
A.甲对,乙不对 B.甲不对,乙对 C.两人都对 D.两人都不对
直线 与半径为 的 相交,且点 到直线 的距离为 ,则 的取值范围是
A. B. C. D.
如图, 的半径为 ,正方形 的边长为 ,点 为正方形 的中心, 垂直 于 点,.若将 绕点 按顺时针方向旋转 ,在旋转过程中, 与正方形 的边只有一个公共点的情况一共出现
A. 次 B. 次 C. 次 D. 次
已知 的半径是 ,点 是直线 上一点且 ,则直线 与 的位置关系是
A.相交 B.相切 C.相离 D.不能确定
平面直角坐标系中, 的圆心坐标为 ,半径为 ,那么 与 轴的位置关系是
A.相交 B.相离 C.相切 D.以上都不是
在平面直角坐标系中,半径为 的圆的圆心在 ,则这个圆与 轴的位置关系是
A.相离 B.相交 C.相切 D.无法确定
在平面直角坐标系中,以点 为圆心, 为半径的圆,一定
A.与 轴相切,与 轴相切 B.与 轴相切,与 轴相交
C.与 轴相交,与 轴相切 D.与 轴相交,与 轴相交
二、填空题(共5题)
如图,线段 的长度为 , 所在直线上方存在点 ,使得 为等腰三角形,设 的面积为 .当 时,满足条件的点 恰有三个.
如图,正方形 的边长为 , 是 的中点, 是 边上的动点,连接 ,以点 为圆心, 长为半径作 .当 与正方形 的边相切时, 的长为 .
如图所示, 的一边 是 的直径,请你添加一个条件,使 是 的切线,你所添加的条件为 .
如图, 的半径为 , 是 延长线上一点,, 切 于 点,那么 的切线 的长为 .
以三角形的一边为直径的圆恰好与另一边相切,则此三角形是 三角形.
三、解答题(共5题)
如图,已知以 为圆心, 为半径的圆交 于点 .若 ,,,则 是 的切线吗?并说明理由.
如图,已知 的直径 与弦 互相垂直,垂足为点 . 的切线 与弦 的延长线相交于点 ,且 ,.
(1)求证:.
(2)求 的半径.
(3)求弦 的长.
下列说法正确吗?若不正确,请画图说明.
(1)垂直于圆的半径的直线一定是这个圆的切线.
(2)过圆的半径的外端的直线一定是这个圆的切线.
如图,点 在 上.
()过点 作 的切线 .
()作出与 垂直的 的切线.
如图所示,已知点 为正方形 对角线 上一点,以点 为圆心,以 长为半径的 与 相切于点 ,与 , 分别相交于点 ,.求证: 与 相切.
答案
1. C
2. D
3. A
4. B
5. A
6. B
7. A
8. C
9. C
10. C
11. B
12. D
13. A
14. C
15. C
16. 或
17. 或
18.
19.
20. 直角
21. 说明 .
22. (1) 是 的切线,
.
,
.
(2) 连接 ,
是直径,
.
,,
.
又 ,
.
的半径为 .
(3) ,,
.
.
又 ,
.
23. (1) 不正确.反例略.
(2) 不正确.反例略.
24. 略
25. 如图所示,连接 ,作 于点 .
因为 与 相切,所以 .
因为四边形 是正方形,
所以 平分 .
所以 .
又因为 ,
所以 与 相切.
