5.3 正方形 课时练习 2021—2022学年浙教版数学八年级下册(word版含答案)
文档属性
| 名称 | 5.3 正方形 课时练习 2021—2022学年浙教版数学八年级下册(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 140.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-04 08:13:02 | ||
图片预览


文档简介
2022年浙教版数学八年级下册
5.3《正方形》课时练习
一、选择题
1.已知正方形的边长为2cm,则其对角线长是( )
A.4cm B.8cm C.cm D.2cm
2.如图,在正方形ABCD中,点E,F分别在BC,CD上,BE=CF,则图中与∠AEB相等的角的个数是( )
A.1 B.2 C.3 D.4
3.下列叙述,错误的是( )
A.对角线互相垂直且相等的平行四边形是正方形
B.对角线互相垂直平分的四边形是菱形
C.对角线互相平分的四边形是平行四边形
D.对角线相等的四边形是矩形
4.小明在学习了正方形之后,给同桌小文出了道题.
从下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD.中选两个作为补充条件,
使 ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
A.①② B.②③ C.①③ D.②④
5.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形
6.已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形
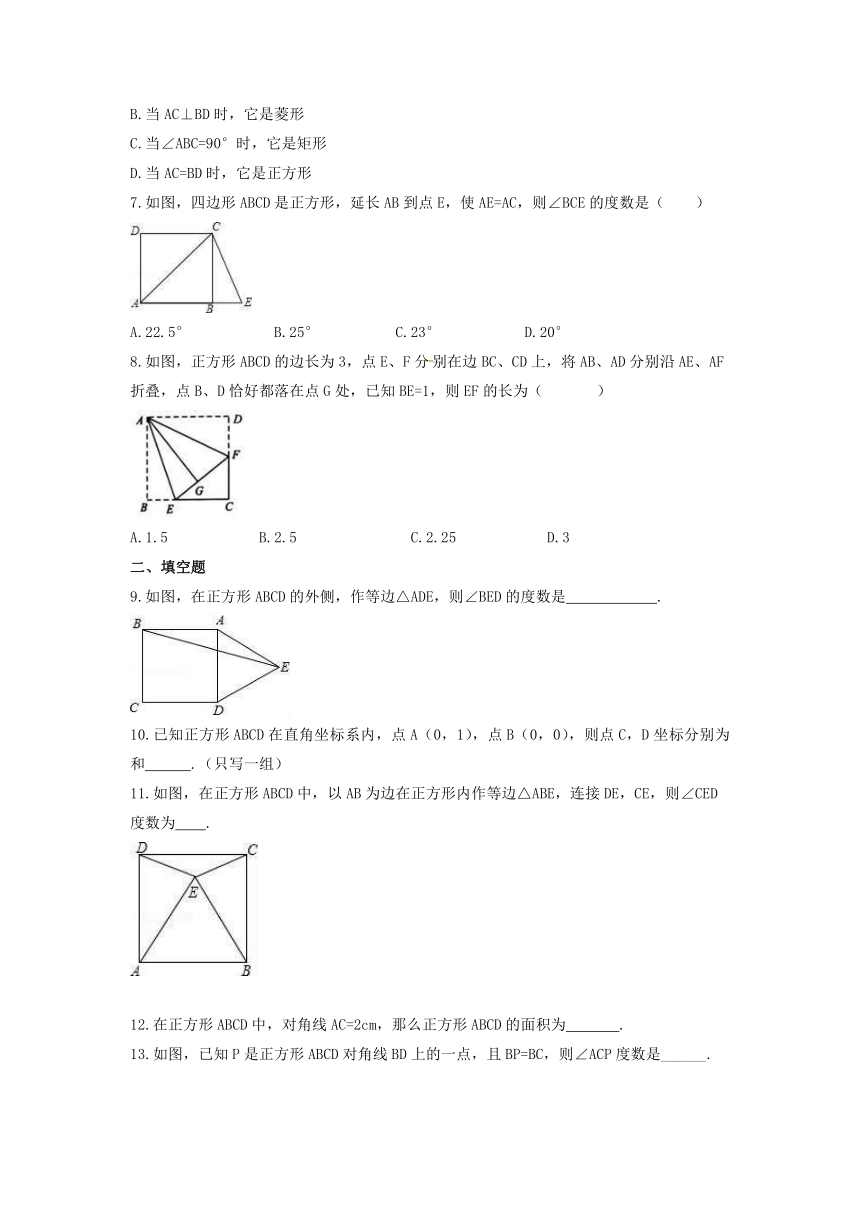
7.如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是( )
A.22.5° B.25° C.23° D.20°
8.如图,正方形ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别沿AE、AF折叠,点B、D恰好都落在点G处,已知BE=1,则EF的长为( )
A.1.5 B.2.5 C.2.25 D.3
二、填空题
9.如图,在正方形ABCD的外侧,作等边△ADE,则∠BED的度数是 .
10.已知正方形ABCD在直角坐标系内,点A(0,1),点B(0,0),则点C,D坐标分别为 和 .(只写一组)
11.如图,在正方形ABCD中,以AB为边在正方形内作等边△ABE,连接DE,CE,则∠CED度数为 .
12.在正方形ABCD中,对角线AC=2cm,那么正方形ABCD的面积为 .
13.如图,已知P是正方形ABCD对角线BD上的一点,且BP=BC,则∠ACP度数是______.
14.如图,在边长为a(a>2)正方形各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=450时,则正方形MNPQ的面积为__________.
三、解答题
15.如图,在正方形ABCD中,点E是BC的中点,连接DE,过点A作AG⊥ED交DE于点F,交CD于点G.
(1)证明:△ADG≌△DCE;
(2)连接BF,证明:AB=FB.
16.已知:在正方形ABCD中,点G是BC边上的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F. 求证:
(1)△ADE≌△BAF;
(2)AF=BF+EF.
17.如图,正方形ABCD中,以对角线BD为边作菱形BDFE,使B,C,E三点在同一直线上,连接BF,交CD与点G.
(1)求证:CG=CE;
(2)若正方形边长为4,求菱形BDFE的面积.
18.如图所示,在正方形ABCD中,M是CD的中点,E是CD上一点,且∠BAE=2∠DAM.
求证:AE=BC+CE.
参考答案
1.D
2.C;
3.D.
4.B
5.D
6.D;
7.A
8.B
9.答案为:45°.
10.答案为:(1,0)和(1,1);
11.答案为:150°.
12.答案为:2
13.答案为:22.5 ;
14.答案为:2;
15.解:(1)∵四边形ABCD是正方形,∴∠ADG=∠C=90°,AD=DC,
又∵AG⊥DE,∴∠DAG+∠ADF=90°=∠CDE+∠ADF,
∴∠DAG=∠CDE,
∴△ADG≌△DCE(ASA);
(2)如图所示,延长DE交AB的延长线于H,
∵E是BC的中点,∴BE=CE,
又∵∠C=∠HBE=90°,∠DEC=∠HEB,
∴△DCE≌△HBE(ASA),∴BH=DC=AB,
即B是AH的中点,
又∵∠AFH=90°,
∴Rt△AFH中,BF=AH=AB.
16.解:(1)由正方形的性质可知:AD=AB,
∵∠BAF+∠ABF=∠BAF+∠DAE=90°,∴∠ABF=∠DAE,
在△ADE与△BAF中,∴△ADE≌△BAF(AAS)
(2)由(1)可知:BF=AE,∴AF=AE+EF=BF+EF
17.解:
18.证明:
5.3《正方形》课时练习
一、选择题
1.已知正方形的边长为2cm,则其对角线长是( )
A.4cm B.8cm C.cm D.2cm
2.如图,在正方形ABCD中,点E,F分别在BC,CD上,BE=CF,则图中与∠AEB相等的角的个数是( )
A.1 B.2 C.3 D.4
3.下列叙述,错误的是( )
A.对角线互相垂直且相等的平行四边形是正方形
B.对角线互相垂直平分的四边形是菱形
C.对角线互相平分的四边形是平行四边形
D.对角线相等的四边形是矩形
4.小明在学习了正方形之后,给同桌小文出了道题.
从下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD.中选两个作为补充条件,
使 ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
A.①② B.②③ C.①③ D.②④
5.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形
6.已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形
7.如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是( )
A.22.5° B.25° C.23° D.20°
8.如图,正方形ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别沿AE、AF折叠,点B、D恰好都落在点G处,已知BE=1,则EF的长为( )
A.1.5 B.2.5 C.2.25 D.3
二、填空题
9.如图,在正方形ABCD的外侧,作等边△ADE,则∠BED的度数是 .
10.已知正方形ABCD在直角坐标系内,点A(0,1),点B(0,0),则点C,D坐标分别为 和 .(只写一组)
11.如图,在正方形ABCD中,以AB为边在正方形内作等边△ABE,连接DE,CE,则∠CED度数为 .
12.在正方形ABCD中,对角线AC=2cm,那么正方形ABCD的面积为 .
13.如图,已知P是正方形ABCD对角线BD上的一点,且BP=BC,则∠ACP度数是______.
14.如图,在边长为a(a>2)正方形各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=450时,则正方形MNPQ的面积为__________.
三、解答题
15.如图,在正方形ABCD中,点E是BC的中点,连接DE,过点A作AG⊥ED交DE于点F,交CD于点G.
(1)证明:△ADG≌△DCE;
(2)连接BF,证明:AB=FB.
16.已知:在正方形ABCD中,点G是BC边上的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F. 求证:
(1)△ADE≌△BAF;
(2)AF=BF+EF.
17.如图,正方形ABCD中,以对角线BD为边作菱形BDFE,使B,C,E三点在同一直线上,连接BF,交CD与点G.
(1)求证:CG=CE;
(2)若正方形边长为4,求菱形BDFE的面积.
18.如图所示,在正方形ABCD中,M是CD的中点,E是CD上一点,且∠BAE=2∠DAM.
求证:AE=BC+CE.
参考答案
1.D
2.C;
3.D.
4.B
5.D
6.D;
7.A
8.B
9.答案为:45°.
10.答案为:(1,0)和(1,1);
11.答案为:150°.
12.答案为:2
13.答案为:22.5 ;
14.答案为:2;
15.解:(1)∵四边形ABCD是正方形,∴∠ADG=∠C=90°,AD=DC,
又∵AG⊥DE,∴∠DAG+∠ADF=90°=∠CDE+∠ADF,
∴∠DAG=∠CDE,
∴△ADG≌△DCE(ASA);
(2)如图所示,延长DE交AB的延长线于H,
∵E是BC的中点,∴BE=CE,
又∵∠C=∠HBE=90°,∠DEC=∠HEB,
∴△DCE≌△HBE(ASA),∴BH=DC=AB,
即B是AH的中点,
又∵∠AFH=90°,
∴Rt△AFH中,BF=AH=AB.
16.解:(1)由正方形的性质可知:AD=AB,
∵∠BAF+∠ABF=∠BAF+∠DAE=90°,∴∠ABF=∠DAE,
在△ADE与△BAF中,∴△ADE≌△BAF(AAS)
(2)由(1)可知:BF=AE,∴AF=AE+EF=BF+EF
17.解:
18.证明:
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
