2021—2022学年浙教版数学九年级下册2.2切线长定理课件(共22张PPT)
文档属性
| 名称 | 2021—2022学年浙教版数学九年级下册2.2切线长定理课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-04 19:48:09 | ||
图片预览





文档简介
(共22张PPT)
2.2 切线长定理
浙教版 九年级下
新知导入
1、了解切线长的概念.了解三角形的内切圆、三角形的内心等概念。2、理解切线长定理,并能熟练运用切线长定理进行解题和证明3、会作已知三角形的内切圆
新知导入
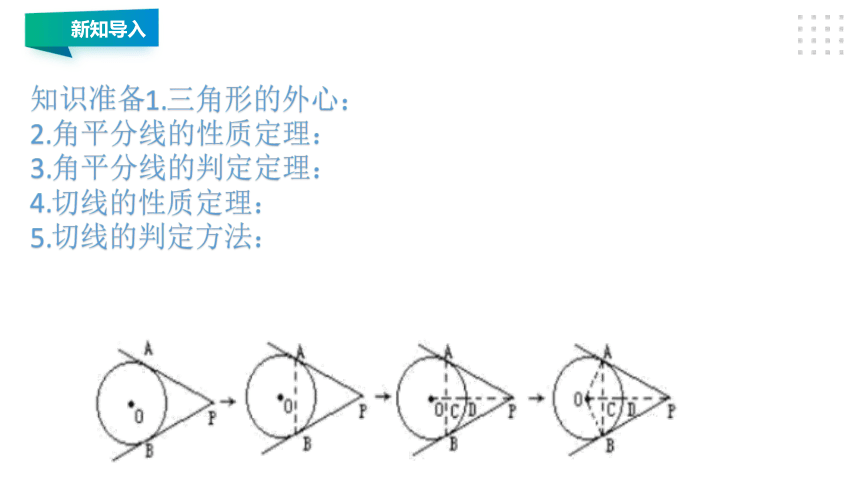
知识准备1.三角形的外心: 2.角平分线的性质定理: 3.角平分线的判定定理: 4.切线的性质定理: 5.切线的判定方法:
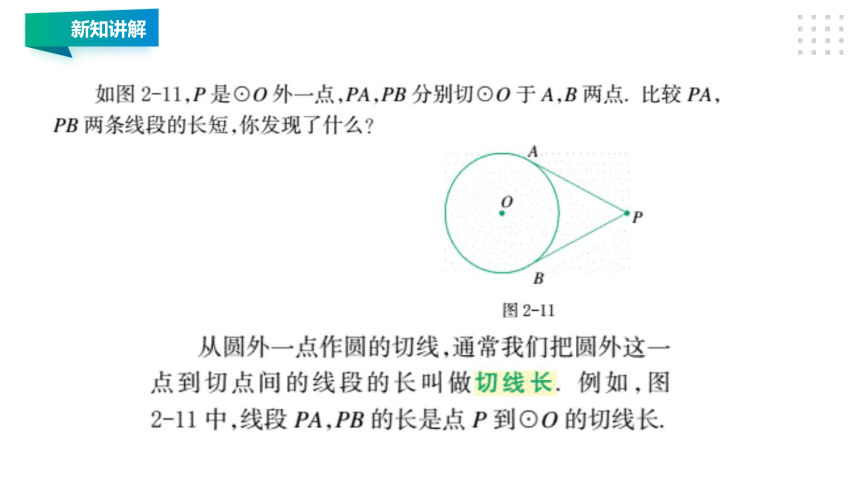
新知讲解
新知讲解
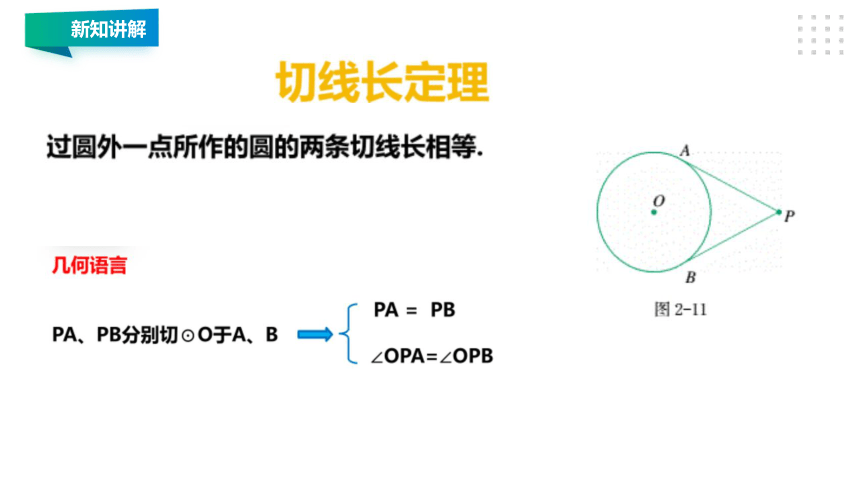
新知讲解
新知讲解
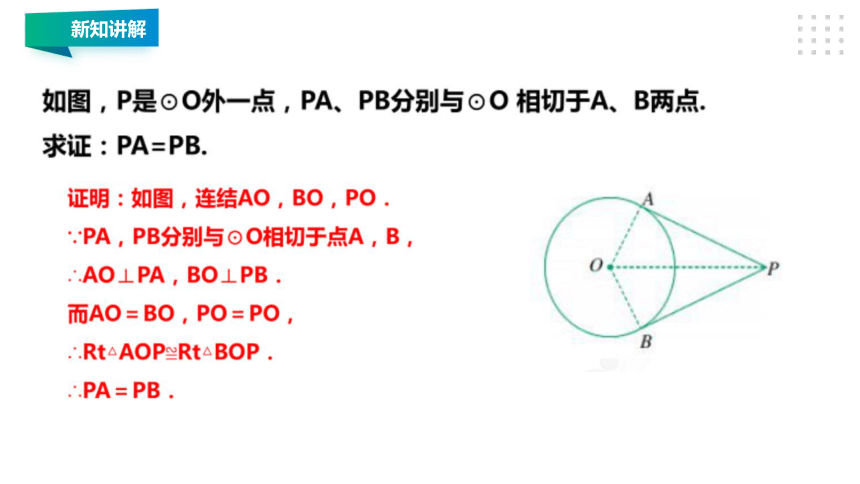
新知讲解
新知讲解
新知讲解
新知讲解
归纳反思
。
P
B
A
O
(3)连结圆心和圆外一点
(2)连结两切点
(1)分别连结圆心和切点
反思:在解决有关圆的切线长问题时,往往需要我们构建基本图形,添加辅助线。
定理拓展
若PA、PB是⊙O的两条切线,A、B为切点,直线OP交于⊙O于点D、E,交AB于C。
B
A
P
O
C
E
D
OA⊥PA,OB ⊥PB,AB ⊥OP
△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP
△ABP △AOB
AO=BO=DO=EO,AP=BP,AC=BC
(2)写出图中所有相等的弧
AD=BD,AE=BE,DAE=DBE
新知讲解
如图:⊙O表示皮带转动装置的一个轮子,传动皮带MA、NB分别为⊙O的切线,A、B为切点,延长MA、NB相交于点P,已知∠APB=600,AP=24cm,求两切点间的距离和弧AB的长(结果精确到1cm)
O
P
A
B
O
P
A
B
M
N
M
N
M
N
新知讲解
1、已知⊙O的半径为5,P是⊙O外一点,PO=10,求点P到⊙O的切线长和两切点间的劣弧长。
O
A
B
M
N
2、已知:在⊙O中,弦AB垂直平分半径ON,过点A、B的切线相交于点M,求证△ABM为等边三角形。
课内练习
新知讲解
例2:如图△ABC的内切圆⊙O与BC、CA、AB分别相切于点D,E,F,且AB=9cm,BC=14cm,CA=13cm,求AF,BD,CE的长.
变式:如图,把三角形改为“直角三角形”,已知AC=13cm,AB=5cm,求内切圆的半径
思维拓展
如图,△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,求∠AOC的度数。
已知,如图,从两个同心圆O的大圆上一点A,作弦AB切小⊙O于C点,AD切小⊙O于E点。
(1)求证:AB=AD;
(2)求证:DE=BC。
尺规作图
如何过⊙O外一点P画出⊙O的切线?
这样的切线能画出几条?
如果∠P=50°,求∠AOB的度数
两条
方法一:借助三角板
中考热点
新知讲解
O
A
B
P
如何用圆规和直尺作出这两条切线呢?
.
思考:已画出切线PA,PB,A,B为切点,则∠OAP=90°,
连接OP,可知A,B 除了在⊙O上,还在怎样的圆上
中考热点
尺规作图
课后练习
如图:EB、EC是⊙O的两条切线,B、C是切点,A、D是⊙O上两点,如果∠E=46°,∠DCF=32°,则∠A的度数是 °.
99
课后练习
如图:EB、EC是⊙O的两条切线,B、C是切点,A、D是⊙O上两点,如果∠E=46°,∠DCF=32°,则∠A的度数是 °.
99
课后练习
13. 已知:⊙O的半径为3cm,点P和圆心O的距离为6cm,经过点P和⊙O的两条切线,求这两条切线的夹角及切线长.
13.
2.2 切线长定理
浙教版 九年级下
新知导入
1、了解切线长的概念.了解三角形的内切圆、三角形的内心等概念。2、理解切线长定理,并能熟练运用切线长定理进行解题和证明3、会作已知三角形的内切圆
新知导入
知识准备1.三角形的外心: 2.角平分线的性质定理: 3.角平分线的判定定理: 4.切线的性质定理: 5.切线的判定方法:
新知讲解
新知讲解
新知讲解
新知讲解
新知讲解
新知讲解
新知讲解
新知讲解
归纳反思
。
P
B
A
O
(3)连结圆心和圆外一点
(2)连结两切点
(1)分别连结圆心和切点
反思:在解决有关圆的切线长问题时,往往需要我们构建基本图形,添加辅助线。
定理拓展
若PA、PB是⊙O的两条切线,A、B为切点,直线OP交于⊙O于点D、E,交AB于C。
B
A
P
O
C
E
D
OA⊥PA,OB ⊥PB,AB ⊥OP
△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP
△ABP △AOB
AO=BO=DO=EO,AP=BP,AC=BC
(2)写出图中所有相等的弧
AD=BD,AE=BE,DAE=DBE
新知讲解
如图:⊙O表示皮带转动装置的一个轮子,传动皮带MA、NB分别为⊙O的切线,A、B为切点,延长MA、NB相交于点P,已知∠APB=600,AP=24cm,求两切点间的距离和弧AB的长(结果精确到1cm)
O
P
A
B
O
P
A
B
M
N
M
N
M
N
新知讲解
1、已知⊙O的半径为5,P是⊙O外一点,PO=10,求点P到⊙O的切线长和两切点间的劣弧长。
O
A
B
M
N
2、已知:在⊙O中,弦AB垂直平分半径ON,过点A、B的切线相交于点M,求证△ABM为等边三角形。
课内练习
新知讲解
例2:如图△ABC的内切圆⊙O与BC、CA、AB分别相切于点D,E,F,且AB=9cm,BC=14cm,CA=13cm,求AF,BD,CE的长.
变式:如图,把三角形改为“直角三角形”,已知AC=13cm,AB=5cm,求内切圆的半径
思维拓展
如图,△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,求∠AOC的度数。
已知,如图,从两个同心圆O的大圆上一点A,作弦AB切小⊙O于C点,AD切小⊙O于E点。
(1)求证:AB=AD;
(2)求证:DE=BC。
尺规作图
如何过⊙O外一点P画出⊙O的切线?
这样的切线能画出几条?
如果∠P=50°,求∠AOB的度数
两条
方法一:借助三角板
中考热点
新知讲解
O
A
B
P
如何用圆规和直尺作出这两条切线呢?
.
思考:已画出切线PA,PB,A,B为切点,则∠OAP=90°,
连接OP,可知A,B 除了在⊙O上,还在怎样的圆上
中考热点
尺规作图
课后练习
如图:EB、EC是⊙O的两条切线,B、C是切点,A、D是⊙O上两点,如果∠E=46°,∠DCF=32°,则∠A的度数是 °.
99
课后练习
如图:EB、EC是⊙O的两条切线,B、C是切点,A、D是⊙O上两点,如果∠E=46°,∠DCF=32°,则∠A的度数是 °.
99
课后练习
13. 已知:⊙O的半径为3cm,点P和圆心O的距离为6cm,经过点P和⊙O的两条切线,求这两条切线的夹角及切线长.
13.
