3.4 简单几何体的表面展开图(2)课件(共24张PPT)
文档属性
| 名称 | 3.4 简单几何体的表面展开图(2)课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-01 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
3.4简单几何体的表面展开图
(第2课时)
浙教版 九年级下册
问题1.圆柱体怎么形成呢?
问题2.你对圆柱还有哪些了解?
新知导入
将矩形绕一边所在直线旋转360°所形成的几何体
如图,圆柱可以看作矩形ABCD绕边BC所在直线旋转一周,其余各边所成的面围成的几何体。
AB,CD旋转所成的面就是圆柱的两个底面,是两个半径相同的圆。
AD旋转所成的面就是圆柱的侧面。
AD不论转到哪个位置,都是圆柱的母线.
圆柱的表面展开图
新知讲解
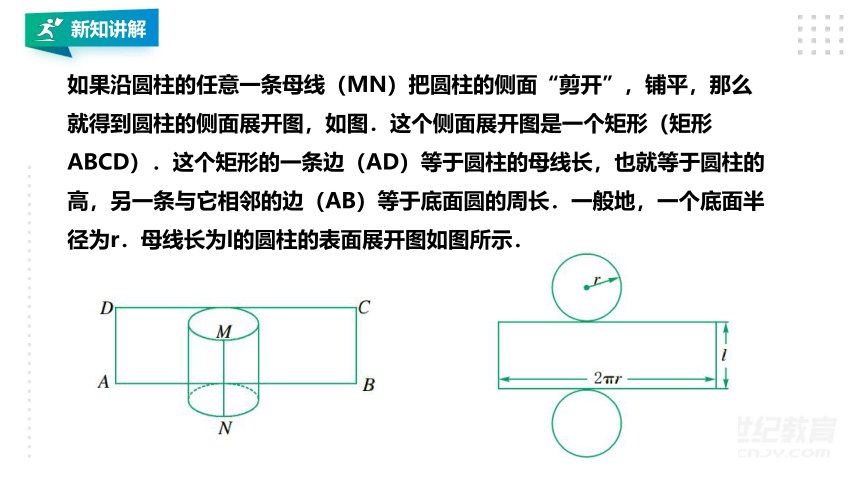
如果沿圆柱的任意一条母线(MN)把圆柱的侧面“剪开”,铺平,那么就得到圆柱的侧面展开图,如图.这个侧面展开图是一个矩形(矩形ABCD).这个矩形的一条边(AD)等于圆柱的母线长,也就等于圆柱的高,另一条与它相邻的边(AB)等于底面圆的周长.一般地,一个底面半径为r.母线长为l的圆柱的表面展开图如图所示.
新知讲解
圆柱的表面展开图的面积:
S表=S侧+2S底
=2πr·h+2πr2=2πr(h+r)=2πr +2πrl.
圆柱的侧面展开图的面积:
S侧=2πr·h=2πrl
新知讲解
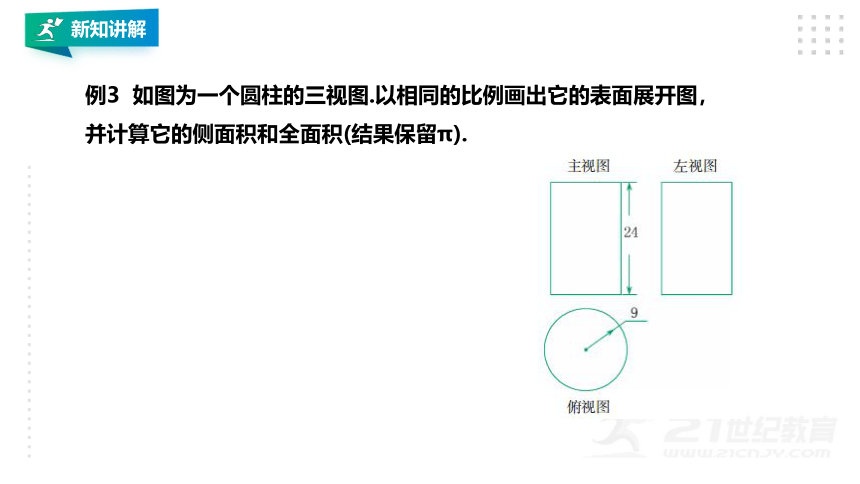
例3 如图为一个圆柱的三视图.以相同的比例画出它的表面展开图,并计算它的侧面积和全面积(结果保留π).
解:所求圆柱的表面展开图如图
S侧=2πrl=2×π×0.9×2.4=4.32π (cm );
S全=2πr +2πrl=2π×0.9 +2π×0.9×2.4=5.94π (cm ).
答:这个圆柱的侧面积为4.32πcm ,全面积为5.94πcm .
新知讲解
圆锥可以看做是一个直角三角形绕它的一条
直角边旋转一周所成的图形,如图所示.
斜边旋转而成的曲面叫做圆锥的侧面.
无论转到什么位置,这条斜边都叫做圆锥的母线.
另一条直角边旋转而成的面叫做圆锥的底面.
圆锥的表面展开图
新知讲解
底面
侧面
A
C
B
表面
新知讲解
圆锥底面圆周上的任意一点与圆锥顶点的连线叫做圆锥的母线(l)
连结顶点与底面圆心的线段
叫做圆锥的高(h)
圆锥的底面半径、高线、母线长之间的关系:
新知讲解
O
P
A
B
r
h
l
(1)将一个圆锥模型的侧面沿它的一条母线剪开、铺平.观察所得的平面图形是什么图形.
(2)圆锥的底面圆周长与侧面展开图有什么关系?
(3)推导圆锥的侧面积公式.
解:(1)以母线为半径的一个扇形.
(2)侧面展开图的弧长等于圆锥底面圆的周长.
(3)S侧=l×2πr=πrl.
新知讲解
圆锥的侧面积和全面积
(1)如图:设圆锥的母线长为l,底面半径为r.则圆锥的侧面积公式为:
(2)全面积公式为:
= πrl +πr2
O
P
A
B
r
h
l
新知讲解
O
P
A
B
r
h
l
) θ
若设圆锥的侧面展开图扇形的圆心角为θ ,则由
得到圆锥的侧面展开图扇形的圆心角度数的计算公式:
圆锥的侧面展开图扇形的圆心角度数的计算公式
新知讲解
例4 圆锥形烟囱帽的母线长为80cm,高38.7cm.
(1)求这个烟囱帽的面积(精确到10cm3).
(2)以1:40的比例画出这个烟囱帽的展开图.
解:(1)∵l=80cm,h=38.7cm,
∴r== ≈70(cm).
∴S=πrl=π×70×80≈1.8×104(cm2).
答:烟囱帽的面积为1.8×104cm2.
新知讲解
(2)以1:40的比例画出这个烟囱帽的展开图.
解:(2)烟囱帽的展开图的扇形圆心角为
θ=×360°=×360°=315°.
按1︰40的比例画这个烟囱帽的展开图如图.
新知讲解
1.一个圆柱的侧面展开后正好是一个正方形,那么圆柱的高等于它的底面( )
A.半径 B.直径 C.周长 D.面积
C
2.圆锥的底面半径是5 cm,侧面展开图的圆心角是180°,圆锥的
是( )
A
课堂练习
3.用一张面积为900cm2的正方形硬纸片围成一个圆柱的侧面,则这个圆柱的底面直径为( )(不计接缝,精确到0.1cm)
A.9.8cm B.9.7cm C.9.6cm D.9.4cm
C
4.如图,圆锥的底面圆的周长是4πcm,母线长是6cm,则该圆锥的侧面展开图的圆心角的度数 .
120°
课堂练习
5.如图,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱帽
(接缝处忽略不计),圆锥底面圆的直径是60 cm,则这块扇形铁皮的半径
是( )
A.40 cm B.50 cm C.60 cm D.80 cm
A
课堂练习
6.一个圆柱的底面直径为20cm,母线长为15cm.求这个圆柱的侧面积和全面积(结果保留π).
解:S侧= 2πrl = 2π×10×15
= 300π(cm2).
S全= 2πr + 2πrl = 2π×10 +2π×10×15
= 500π(cm2).
答:圆柱的侧面积为300πcm2,全面积为500πcm2.
课堂练习
解:设圆锥的母线长是R,底面半径是r.
由题意得πR=2πr,所以R=2r,
即R∶r=2∶1.
(2)∠BAC的度数;
解:易知∠CAO=∠BAO,AO⊥BC,
在Rt△AOB中,2OB=AB,
所以∠OAB=30°,所以∠BAC=60°.
课堂练习
课堂练习
h
高
底面半径
r
母线
2.圆锥的高,底面半径, 母线长之间的关系是:
圆锥的侧面积:
圆锥的全面积:
圆锥侧面展开图的圆心角:
1.圆柱的侧面展开图的面积:
S侧=2πr·h=2πrl
圆柱的表面展开图的面积:
S表=S侧+2S底=2πr·h+2πr2=2πr(h+r)=2πr +2πrl.
https://www.21cnjy.com/help/help_extract.php
3.4简单几何体的表面展开图
(第2课时)
浙教版 九年级下册
问题1.圆柱体怎么形成呢?
问题2.你对圆柱还有哪些了解?
新知导入
将矩形绕一边所在直线旋转360°所形成的几何体
如图,圆柱可以看作矩形ABCD绕边BC所在直线旋转一周,其余各边所成的面围成的几何体。
AB,CD旋转所成的面就是圆柱的两个底面,是两个半径相同的圆。
AD旋转所成的面就是圆柱的侧面。
AD不论转到哪个位置,都是圆柱的母线.
圆柱的表面展开图
新知讲解
如果沿圆柱的任意一条母线(MN)把圆柱的侧面“剪开”,铺平,那么就得到圆柱的侧面展开图,如图.这个侧面展开图是一个矩形(矩形ABCD).这个矩形的一条边(AD)等于圆柱的母线长,也就等于圆柱的高,另一条与它相邻的边(AB)等于底面圆的周长.一般地,一个底面半径为r.母线长为l的圆柱的表面展开图如图所示.
新知讲解
圆柱的表面展开图的面积:
S表=S侧+2S底
=2πr·h+2πr2=2πr(h+r)=2πr +2πrl.
圆柱的侧面展开图的面积:
S侧=2πr·h=2πrl
新知讲解
例3 如图为一个圆柱的三视图.以相同的比例画出它的表面展开图,并计算它的侧面积和全面积(结果保留π).
解:所求圆柱的表面展开图如图
S侧=2πrl=2×π×0.9×2.4=4.32π (cm );
S全=2πr +2πrl=2π×0.9 +2π×0.9×2.4=5.94π (cm ).
答:这个圆柱的侧面积为4.32πcm ,全面积为5.94πcm .
新知讲解
圆锥可以看做是一个直角三角形绕它的一条
直角边旋转一周所成的图形,如图所示.
斜边旋转而成的曲面叫做圆锥的侧面.
无论转到什么位置,这条斜边都叫做圆锥的母线.
另一条直角边旋转而成的面叫做圆锥的底面.
圆锥的表面展开图
新知讲解
底面
侧面
A
C
B
表面
新知讲解
圆锥底面圆周上的任意一点与圆锥顶点的连线叫做圆锥的母线(l)
连结顶点与底面圆心的线段
叫做圆锥的高(h)
圆锥的底面半径、高线、母线长之间的关系:
新知讲解
O
P
A
B
r
h
l
(1)将一个圆锥模型的侧面沿它的一条母线剪开、铺平.观察所得的平面图形是什么图形.
(2)圆锥的底面圆周长与侧面展开图有什么关系?
(3)推导圆锥的侧面积公式.
解:(1)以母线为半径的一个扇形.
(2)侧面展开图的弧长等于圆锥底面圆的周长.
(3)S侧=l×2πr=πrl.
新知讲解
圆锥的侧面积和全面积
(1)如图:设圆锥的母线长为l,底面半径为r.则圆锥的侧面积公式为:
(2)全面积公式为:
= πrl +πr2
O
P
A
B
r
h
l
新知讲解
O
P
A
B
r
h
l
) θ
若设圆锥的侧面展开图扇形的圆心角为θ ,则由
得到圆锥的侧面展开图扇形的圆心角度数的计算公式:
圆锥的侧面展开图扇形的圆心角度数的计算公式
新知讲解
例4 圆锥形烟囱帽的母线长为80cm,高38.7cm.
(1)求这个烟囱帽的面积(精确到10cm3).
(2)以1:40的比例画出这个烟囱帽的展开图.
解:(1)∵l=80cm,h=38.7cm,
∴r== ≈70(cm).
∴S=πrl=π×70×80≈1.8×104(cm2).
答:烟囱帽的面积为1.8×104cm2.
新知讲解
(2)以1:40的比例画出这个烟囱帽的展开图.
解:(2)烟囱帽的展开图的扇形圆心角为
θ=×360°=×360°=315°.
按1︰40的比例画这个烟囱帽的展开图如图.
新知讲解
1.一个圆柱的侧面展开后正好是一个正方形,那么圆柱的高等于它的底面( )
A.半径 B.直径 C.周长 D.面积
C
2.圆锥的底面半径是5 cm,侧面展开图的圆心角是180°,圆锥的
是( )
A
课堂练习
3.用一张面积为900cm2的正方形硬纸片围成一个圆柱的侧面,则这个圆柱的底面直径为( )(不计接缝,精确到0.1cm)
A.9.8cm B.9.7cm C.9.6cm D.9.4cm
C
4.如图,圆锥的底面圆的周长是4πcm,母线长是6cm,则该圆锥的侧面展开图的圆心角的度数 .
120°
课堂练习
5.如图,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱帽
(接缝处忽略不计),圆锥底面圆的直径是60 cm,则这块扇形铁皮的半径
是( )
A.40 cm B.50 cm C.60 cm D.80 cm
A
课堂练习
6.一个圆柱的底面直径为20cm,母线长为15cm.求这个圆柱的侧面积和全面积(结果保留π).
解:S侧= 2πrl = 2π×10×15
= 300π(cm2).
S全= 2πr + 2πrl = 2π×10 +2π×10×15
= 500π(cm2).
答:圆柱的侧面积为300πcm2,全面积为500πcm2.
课堂练习
解:设圆锥的母线长是R,底面半径是r.
由题意得πR=2πr,所以R=2r,
即R∶r=2∶1.
(2)∠BAC的度数;
解:易知∠CAO=∠BAO,AO⊥BC,
在Rt△AOB中,2OB=AB,
所以∠OAB=30°,所以∠BAC=60°.
课堂练习
课堂练习
h
高
底面半径
r
母线
2.圆锥的高,底面半径, 母线长之间的关系是:
圆锥的侧面积:
圆锥的全面积:
圆锥侧面展开图的圆心角:
1.圆柱的侧面展开图的面积:
S侧=2πr·h=2πrl
圆柱的表面展开图的面积:
S表=S侧+2S底=2πr·h+2πr2=2πr(h+r)=2πr +2πrl.
https://www.21cnjy.com/help/help_extract.php
