2021-2022学年浙教版八年级数学上册《第5章一次函数》期末综合复习训练1(Word版含解析)
文档属性
| 名称 | 2021-2022学年浙教版八年级数学上册《第5章一次函数》期末综合复习训练1(Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 182.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-06 20:54:55 | ||
图片预览



文档简介
2021-2022学年浙教版八年级数学上册《第5章一次函数》期末综合复习训练1(附答案)
1.把一个长为8,宽为3的长方形的宽增加x(0≤x<5),长不变,所得长方形的面积y关于x的函数表达式为( )
A.y=24﹣x B.y=8x﹣24 C.y=8x D.y=8x+24
2.下列图形中,不能代表y是x函数的是( )
A.B.C.D.
3.在函数y=中,自变量x的取值范围是( )
A.x≥0 B.x≠2 C.x≥0且x≠2 D.0≤x≤2
4.一次函数y=ax+a(a<0)的图象不经过象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.已知正比例函数y=kx的图象与x轴的夹角为30°,且y随x的增大而减小,则k的值为( )
A. B.﹣ C. D.﹣
6.在平面直角坐标系中,一次函数y=x+1的图象是( )
A.B.C.D.
7.函数y=2x+2的图象如图所示,下列说法正确的是( )
A.当x>0时,y>2 B.当x<0时,y<0
C.当x>0时,y>0 D.当x>﹣1时,y>2
8.若正比例函数y=(2﹣k)x的图象经过第二、四象限,则k的取值范围是( )
A.k<﹣2 B.k<2 C.k>﹣2 D.k>2
9.如图,直线y=kx+b(k≠0)过点A(0,5),B(﹣4,0),则关于x的方程kx+b=0的解是( )
A.x=﹣4 B.x=5 C.x=﹣ D.x=﹣
10.如图,直线y=x+b和y=kx+2与x轴分别交于点A(﹣2,0),点B(3,0),则不等式组的解集为( )
A.x<﹣2 B.x>3 C.﹣2<x<3 D.x<﹣2或x>3
11.直线y=﹣3x﹣7在y轴上的截距是 .
12.点A(x1,y1),点B(x2,y2)是一次函数y=3x+b图象上的两个点,且x1<x2,那么y1 y2(填“>”或“<”).
13.一次函数y=(2m﹣1)x+m的函数值y随x值的增大而增大,则m的取值范围是 .
14.将直线y=﹣x﹣1向上平移4个单位所得的直线表达式为 .
15.一次函数y=kx+b的图象如图所示,则关于x的方程kx+b=﹣1的解为 .
16.如图,直线y=kx+b上有一点P(﹣1,3),回答下列问题:
(1)关于x的方程kx+b=3的解是 ;
(2)关于x的不等式kx+b>3的解是 ;
(3)关于x的不等式kx+b﹣3<0的解是 .
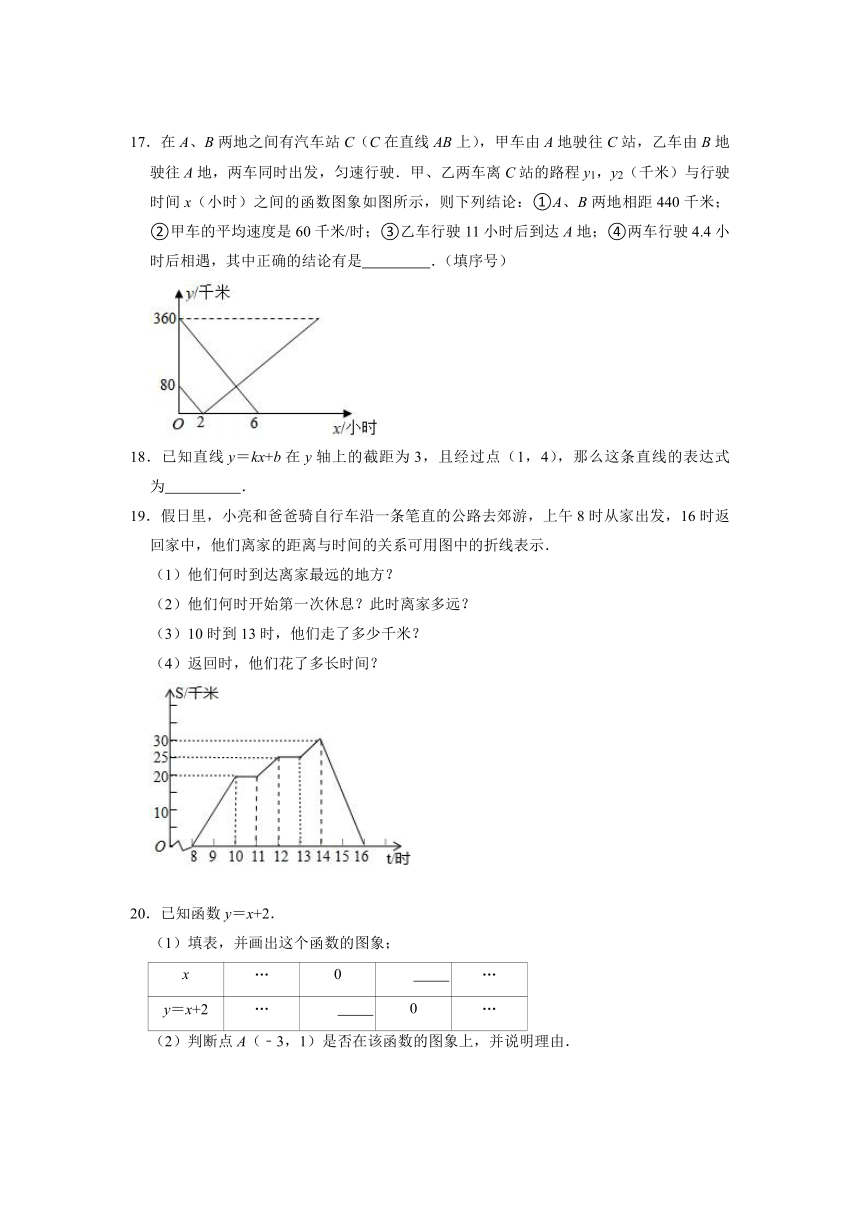
17.在A、B两地之间有汽车站C(C在直线AB上),甲车由A地驶往C站,乙车由B地驶往A地,两车同时出发,匀速行驶.甲、乙两车离C站的路程y1,y2(千米)与行驶时间x(小时)之间的函数图象如图所示,则下列结论:①A、B两地相距440千米;②甲车的平均速度是60千米/时;③乙车行驶11小时后到达A地;④两车行驶4.4小时后相遇,其中正确的结论有是 .(填序号)
18.已知直线y=kx+b在y轴上的截距为3,且经过点(1,4),那么这条直线的表达式为 .
19.假日里,小亮和爸爸骑自行车沿一条笔直的公路去郊游,上午8时从家出发,16时返回家中,他们离家的距离与时间的关系可用图中的折线表示.
(1)他们何时到达离家最远的地方?
(2)他们何时开始第一次休息?此时离家多远?
(3)10时到13时,他们走了多少千米?
(4)返回时,他们花了多长时间?
20.已知函数y=x+2.
(1)填表,并画出这个函数的图象;
x … 0 …
y=x+2 … 0 …
(2)判断点A(﹣3,1)是否在该函数的图象上,并说明理由.
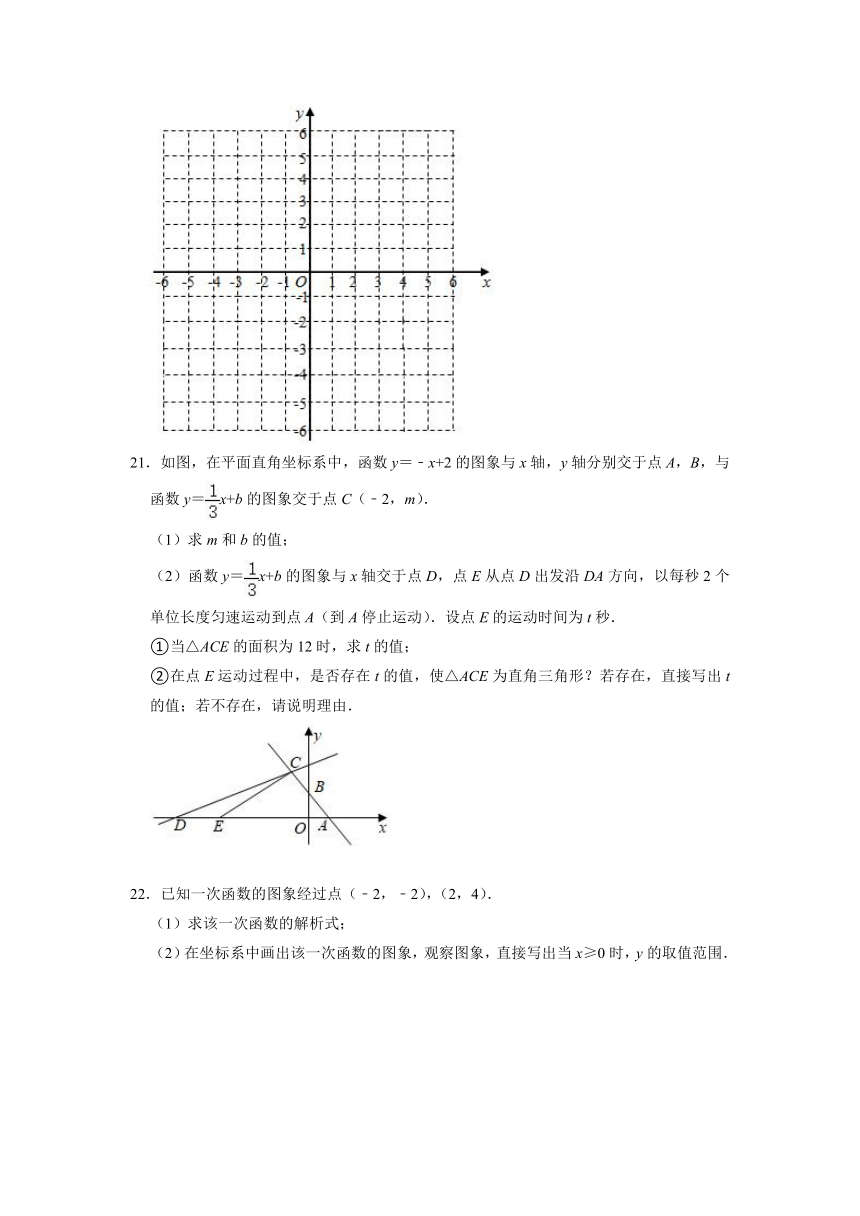
21.如图,在平面直角坐标系中,函数y=﹣x+2的图象与x轴,y轴分别交于点A,B,与函数y=x+b的图象交于点C(﹣2,m).
(1)求m和b的值;
(2)函数y=x+b的图象与x轴交于点D,点E从点D出发沿DA方向,以每秒2个单位长度匀速运动到点A(到A停止运动).设点E的运动时间为t秒.
①当△ACE的面积为12时,求t的值;
②在点E运动过程中,是否存在t的值,使△ACE为直角三角形?若存在,直接写出t的值;若不存在,请说明理由.
22.已知一次函数的图象经过点(﹣2,﹣2),(2,4).
(1)求该一次函数的解析式;
(2)在坐标系中画出该一次函数的图象,观察图象,直接写出当x≥0时,y的取值范围.
23.由于疫情的影响,“地摊经济“成为了很多人经济来原的一种形式.李叔叔从市场得知如下信息:
A商品 B商品
进价(元/件) 35 5
售价(元/件) 45 8
李叔叔计划购进A.B商品共100件进行销售,设购进A商品x件,A.B商品全部销售完后获得利润为y元.
(1)求出y与x之间的函数关系式;
(2)若李叔叔用不超过2000元资金一次性购进A.B两种商品,则如何进货,才能使得获利最大?并求出最大利润.
24.某年5月,我国南方某省A,B两市遭受严重洪涝灾害,1.5万人被迫转移,邻近县市C,D获知A,B两市分别急需救灾物资200吨和300吨的消息后,决定调运物资支援灾区.已知C市有救灾物资240吨,D市有救灾物资260吨,现将这些救灾物资全部调往A,B两市.已知从C市运往A,B两市的运费分别为每吨20元和25元,从D市运往A,B两市的运费分别为每吨15元和30元,设从D市运往B市的救灾物资为x吨.
(1)设C,D两市的总运费为w元,求w与x之间的函数关系式.
(2)怎样安排调运使得总运费最小,并求出最小值.
参考答案
1.解:变化后长方形的宽为(x+3),长为8,因此面积y=8(x+3)=8x+24,
故选:D.
2.解:A、满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故此选项不符合题意;
B、满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故此选项不符合题意;
C、不满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故此选项符合题意;
D、满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故此选项不符合题意;
故选:C.
3.解:根据二次根式的意义可知:x≥0.
根据分式的意义可知:x﹣2≠0,即x≠2.
∴x≥0且x≠2.
故选:C.
4.解:∵y=ax+a(a<0),k=a<0,b=a<0,
∴该函数经过第二、三、四象限,不经过第一象限,
故选:A.
5.解:∵正比例函数y=kx,y随x的增大而减小,
∴k<0,如图:
在正比例函数y=kx第二象限的图象上取点A,作AB⊥x轴于B,
设AB=m,
∵∠AOB=30°,
∴OA=2m,OB=m,
∴A(﹣m,m),
将A(﹣m,m)代入y=kx得:
m=﹣m k,
解得k=﹣,
故选:D.
6.解:一次函数y=x+1中,令x=0,则y=1;令y=0,则x=﹣1,
∴一次函数y=x+1的图象经过点(0,1)和(﹣1,0),
∴一次函数y=x+1的图象经过一、二、三象限,
故选:C.
7.解:在y=2x+2中,令x=0时,y=2,
∴当x>0时,y>2,
故选:A.
8.解:∵正比例函数y=(2﹣k)x的图象经过第二、四象限,
∴2﹣k<0,
解得:k>2,
故选:D.
9.解:∵直线y=kx+b(k≠0)过点B(﹣4,0),
即当x=﹣4时,y=0,
∴关于x的方程kx+b=0的解是x=﹣4.
故选:A.
10.解:∵直线y=x+b和y=kx+2与x轴分别交于点A(﹣2,0),点B(3,0),
∴解集为﹣2<x<3,
故选:C.
11.解:当x=0时,y=﹣3×0﹣7=﹣7,
∴直线y=﹣3x﹣7在y轴上的截距是﹣7.
故答案为:﹣7.
12.解:∵k=3>0,
∴y随x的增大而增大.
又∵x1<x2,
∴y1<y2.
故答案为:<.
13.解:∵y随x的增大而增大,
∴2m﹣1>0.
解得:m>.
故答案为:m>.
14.解:将直线y=﹣x﹣1向上平移4个单位所得的直线表达式为:
y=﹣x﹣1+4,即y=﹣x+3.
故答案为:y=﹣x+3.
15.解:∵一次函数y=kx+b的图象过点(,﹣1),
∴关于x的方程kx+b=﹣1的解是x=,
故答案为:x=.
16.解:(1)∵点P(﹣1,3)直线y=kx+b的图象上一点,
∴当x=﹣1时,y=kx+b=3,
∴关于x的方程kx+b=3的解是x=﹣1,
故答案为:x=﹣1;
(2)由函数图象可知,当x>﹣1时函数图象在3的上方,
∴不等式kx+b>3的解集是x>﹣1.
故答案为:x>﹣1;
(3)由函数图象可知,当x<﹣1时函数图象在3的下方,
∴不等式kx+b<的解集是x<﹣1.
故答案为:x<﹣1.
17.解:A、B两地相距=360+80=440(千米),故①正确,
甲车的平均速度==60(千米/小时),故②正确,
乙车的平均速度==40千米/小时,440÷40=11(小时),
∴乙车行驶11小时后到达A地,故③正确,
设t小时相遇,则有:(60+40)t=440,
解得:t=4.4(小时),
∴两车行驶4.4小时后相遇,故④正确,
故答案为:①②③④.
18.解:∵直线y=kx+b在y轴上的截距为3,
∴b=3,
∴y=kx+3,
∵经过点(1,4),
∴4=k+3,
∴k=1,
∴这条直线的解析式是y=x+3.
故答案是:y=x+3.
19.解:(1)由图象知,在图形的最高点就是他们到达离家最远30千米的地方.此时对应的时刻是14时;
(2)休息的时候路程为0,即开始出现的第一个水平状态的时刻,由图象可知,他们第一次休息的时刻是在10时,此时离家20千米;
(3)由图象知,在10时到13时这段时间内,他们只在11时到12时运动,对应的路程差为5km;
(4)由图形可知,返回时是14时到16时,所用时间是2小时.
20.解:(1)当x=0时,y=0+2=2;
当y=0时,x+2=0,解得:x=﹣2.
描点、连线,画出函数图象,如图所示.
故答案为:2;﹣2.
(2)点A(﹣3,1)不在该函数的图象上,理由如下:
当x=﹣3时,y=﹣3+2=﹣1,﹣1≠1,
∴点A(﹣3,1)不在该函数的图象上.
21.解:(1)∵点C(﹣2,m)在直线y=﹣x+2上,
∴m=﹣(﹣2)+2=2+2=4,
∴点C(﹣2,4),
∵函数y=x+b的图象过点C(﹣2,4),
∴4=×(﹣2)+b,得b=,
即m的值是4,b的值是;
(2)①∵函数y=﹣x+2的图象与x轴,y轴分别交于点A,B,
∴点A(2,0),点B(0,2),
∵函数y=x+的图象与x轴交于点D,
∴点D的坐标为(﹣14,0),
∴AD=16,
∵△ACE的面积为12,
∴=12,
解得,t=5.
即当△ACE的面积为12时,t的值是5;
②当t=4或t=6时,△ACE是直角三角形,
理由:当∠ACE=90°时,AC⊥CE,
∵点A(2,0),点B(0,2),点C(﹣2,4),点D(﹣14,0),
∴OA=OB,AC=4,
∴∠BAO=45°,
∴∠CAE=45°,
∴∠CEA=45°,
∴CA=CE=4,
∴AE=8,
∵AE=16﹣2t,
∴8=16﹣2t,
解得,t=4;
当∠CEA=90°时,
∵AC=4,∠CAE=45°,
∴AE=4,
∵AE=16﹣2t,
∴4=16﹣2t,
解得,t=6;
由上可得,当t=4或t=6时,△ACE是直角三角形.
22.解:(1)设函数的解析式是y=kx+b,
根据题意得:,
解得:,
则函数的解析式是y=x+1;
(2)画出函数图象如图所示;
观察图象,当x≥0时,y≥1.
23.解:(1)由题意可得:y=(45﹣35)x+(8﹣5)(100﹣x)=7x+300,
∴y与x之间的函数关系式为y=7x+300;
(2)由题意可得:35x+5(100﹣x)≤2000,
解得:x≤50,
又∵x≥0,
∴0≤x≤50,
∵y=7x+300,7>0,
∴y随x的增大而增大,
∴当x=50时,可获得最大利润,最大利润为:
y=7×50+300=650(元),
100﹣x=100﹣50=50(件).
答:当购进A种商品50件,B种商品50件时,可使得A、B商品全部销售完后获得的利润最大,最大利润650元.
24.解:由题意可得:w=20(x﹣60)+25(300﹣x)+15(260﹣x)+30x=10x+10200,
∴w=10x+10200(60≤x≤260);
(2)∵w=10x+10200(60≤x≤260)
∴k=10>0,
∴w随x的增大而增大,
∴当x=60时,w有最小值为10800元,
答:从D市运往B市的救灾物资为60吨,从D市运往A市的救灾物资为200吨,从C市运往B市的救灾物资为240吨,从C市运往A市的救灾物资为0吨,此时总运费最小,最小值为10800元.
1.把一个长为8,宽为3的长方形的宽增加x(0≤x<5),长不变,所得长方形的面积y关于x的函数表达式为( )
A.y=24﹣x B.y=8x﹣24 C.y=8x D.y=8x+24
2.下列图形中,不能代表y是x函数的是( )
A.B.C.D.
3.在函数y=中,自变量x的取值范围是( )
A.x≥0 B.x≠2 C.x≥0且x≠2 D.0≤x≤2
4.一次函数y=ax+a(a<0)的图象不经过象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.已知正比例函数y=kx的图象与x轴的夹角为30°,且y随x的增大而减小,则k的值为( )
A. B.﹣ C. D.﹣
6.在平面直角坐标系中,一次函数y=x+1的图象是( )
A.B.C.D.
7.函数y=2x+2的图象如图所示,下列说法正确的是( )
A.当x>0时,y>2 B.当x<0时,y<0
C.当x>0时,y>0 D.当x>﹣1时,y>2
8.若正比例函数y=(2﹣k)x的图象经过第二、四象限,则k的取值范围是( )
A.k<﹣2 B.k<2 C.k>﹣2 D.k>2
9.如图,直线y=kx+b(k≠0)过点A(0,5),B(﹣4,0),则关于x的方程kx+b=0的解是( )
A.x=﹣4 B.x=5 C.x=﹣ D.x=﹣
10.如图,直线y=x+b和y=kx+2与x轴分别交于点A(﹣2,0),点B(3,0),则不等式组的解集为( )
A.x<﹣2 B.x>3 C.﹣2<x<3 D.x<﹣2或x>3
11.直线y=﹣3x﹣7在y轴上的截距是 .
12.点A(x1,y1),点B(x2,y2)是一次函数y=3x+b图象上的两个点,且x1<x2,那么y1 y2(填“>”或“<”).
13.一次函数y=(2m﹣1)x+m的函数值y随x值的增大而增大,则m的取值范围是 .
14.将直线y=﹣x﹣1向上平移4个单位所得的直线表达式为 .
15.一次函数y=kx+b的图象如图所示,则关于x的方程kx+b=﹣1的解为 .
16.如图,直线y=kx+b上有一点P(﹣1,3),回答下列问题:
(1)关于x的方程kx+b=3的解是 ;
(2)关于x的不等式kx+b>3的解是 ;
(3)关于x的不等式kx+b﹣3<0的解是 .
17.在A、B两地之间有汽车站C(C在直线AB上),甲车由A地驶往C站,乙车由B地驶往A地,两车同时出发,匀速行驶.甲、乙两车离C站的路程y1,y2(千米)与行驶时间x(小时)之间的函数图象如图所示,则下列结论:①A、B两地相距440千米;②甲车的平均速度是60千米/时;③乙车行驶11小时后到达A地;④两车行驶4.4小时后相遇,其中正确的结论有是 .(填序号)
18.已知直线y=kx+b在y轴上的截距为3,且经过点(1,4),那么这条直线的表达式为 .
19.假日里,小亮和爸爸骑自行车沿一条笔直的公路去郊游,上午8时从家出发,16时返回家中,他们离家的距离与时间的关系可用图中的折线表示.
(1)他们何时到达离家最远的地方?
(2)他们何时开始第一次休息?此时离家多远?
(3)10时到13时,他们走了多少千米?
(4)返回时,他们花了多长时间?
20.已知函数y=x+2.
(1)填表,并画出这个函数的图象;
x … 0 …
y=x+2 … 0 …
(2)判断点A(﹣3,1)是否在该函数的图象上,并说明理由.
21.如图,在平面直角坐标系中,函数y=﹣x+2的图象与x轴,y轴分别交于点A,B,与函数y=x+b的图象交于点C(﹣2,m).
(1)求m和b的值;
(2)函数y=x+b的图象与x轴交于点D,点E从点D出发沿DA方向,以每秒2个单位长度匀速运动到点A(到A停止运动).设点E的运动时间为t秒.
①当△ACE的面积为12时,求t的值;
②在点E运动过程中,是否存在t的值,使△ACE为直角三角形?若存在,直接写出t的值;若不存在,请说明理由.
22.已知一次函数的图象经过点(﹣2,﹣2),(2,4).
(1)求该一次函数的解析式;
(2)在坐标系中画出该一次函数的图象,观察图象,直接写出当x≥0时,y的取值范围.
23.由于疫情的影响,“地摊经济“成为了很多人经济来原的一种形式.李叔叔从市场得知如下信息:
A商品 B商品
进价(元/件) 35 5
售价(元/件) 45 8
李叔叔计划购进A.B商品共100件进行销售,设购进A商品x件,A.B商品全部销售完后获得利润为y元.
(1)求出y与x之间的函数关系式;
(2)若李叔叔用不超过2000元资金一次性购进A.B两种商品,则如何进货,才能使得获利最大?并求出最大利润.
24.某年5月,我国南方某省A,B两市遭受严重洪涝灾害,1.5万人被迫转移,邻近县市C,D获知A,B两市分别急需救灾物资200吨和300吨的消息后,决定调运物资支援灾区.已知C市有救灾物资240吨,D市有救灾物资260吨,现将这些救灾物资全部调往A,B两市.已知从C市运往A,B两市的运费分别为每吨20元和25元,从D市运往A,B两市的运费分别为每吨15元和30元,设从D市运往B市的救灾物资为x吨.
(1)设C,D两市的总运费为w元,求w与x之间的函数关系式.
(2)怎样安排调运使得总运费最小,并求出最小值.
参考答案
1.解:变化后长方形的宽为(x+3),长为8,因此面积y=8(x+3)=8x+24,
故选:D.
2.解:A、满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故此选项不符合题意;
B、满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故此选项不符合题意;
C、不满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故此选项符合题意;
D、满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故此选项不符合题意;
故选:C.
3.解:根据二次根式的意义可知:x≥0.
根据分式的意义可知:x﹣2≠0,即x≠2.
∴x≥0且x≠2.
故选:C.
4.解:∵y=ax+a(a<0),k=a<0,b=a<0,
∴该函数经过第二、三、四象限,不经过第一象限,
故选:A.
5.解:∵正比例函数y=kx,y随x的增大而减小,
∴k<0,如图:
在正比例函数y=kx第二象限的图象上取点A,作AB⊥x轴于B,
设AB=m,
∵∠AOB=30°,
∴OA=2m,OB=m,
∴A(﹣m,m),
将A(﹣m,m)代入y=kx得:
m=﹣m k,
解得k=﹣,
故选:D.
6.解:一次函数y=x+1中,令x=0,则y=1;令y=0,则x=﹣1,
∴一次函数y=x+1的图象经过点(0,1)和(﹣1,0),
∴一次函数y=x+1的图象经过一、二、三象限,
故选:C.
7.解:在y=2x+2中,令x=0时,y=2,
∴当x>0时,y>2,
故选:A.
8.解:∵正比例函数y=(2﹣k)x的图象经过第二、四象限,
∴2﹣k<0,
解得:k>2,
故选:D.
9.解:∵直线y=kx+b(k≠0)过点B(﹣4,0),
即当x=﹣4时,y=0,
∴关于x的方程kx+b=0的解是x=﹣4.
故选:A.
10.解:∵直线y=x+b和y=kx+2与x轴分别交于点A(﹣2,0),点B(3,0),
∴解集为﹣2<x<3,
故选:C.
11.解:当x=0时,y=﹣3×0﹣7=﹣7,
∴直线y=﹣3x﹣7在y轴上的截距是﹣7.
故答案为:﹣7.
12.解:∵k=3>0,
∴y随x的增大而增大.
又∵x1<x2,
∴y1<y2.
故答案为:<.
13.解:∵y随x的增大而增大,
∴2m﹣1>0.
解得:m>.
故答案为:m>.
14.解:将直线y=﹣x﹣1向上平移4个单位所得的直线表达式为:
y=﹣x﹣1+4,即y=﹣x+3.
故答案为:y=﹣x+3.
15.解:∵一次函数y=kx+b的图象过点(,﹣1),
∴关于x的方程kx+b=﹣1的解是x=,
故答案为:x=.
16.解:(1)∵点P(﹣1,3)直线y=kx+b的图象上一点,
∴当x=﹣1时,y=kx+b=3,
∴关于x的方程kx+b=3的解是x=﹣1,
故答案为:x=﹣1;
(2)由函数图象可知,当x>﹣1时函数图象在3的上方,
∴不等式kx+b>3的解集是x>﹣1.
故答案为:x>﹣1;
(3)由函数图象可知,当x<﹣1时函数图象在3的下方,
∴不等式kx+b<的解集是x<﹣1.
故答案为:x<﹣1.
17.解:A、B两地相距=360+80=440(千米),故①正确,
甲车的平均速度==60(千米/小时),故②正确,
乙车的平均速度==40千米/小时,440÷40=11(小时),
∴乙车行驶11小时后到达A地,故③正确,
设t小时相遇,则有:(60+40)t=440,
解得:t=4.4(小时),
∴两车行驶4.4小时后相遇,故④正确,
故答案为:①②③④.
18.解:∵直线y=kx+b在y轴上的截距为3,
∴b=3,
∴y=kx+3,
∵经过点(1,4),
∴4=k+3,
∴k=1,
∴这条直线的解析式是y=x+3.
故答案是:y=x+3.
19.解:(1)由图象知,在图形的最高点就是他们到达离家最远30千米的地方.此时对应的时刻是14时;
(2)休息的时候路程为0,即开始出现的第一个水平状态的时刻,由图象可知,他们第一次休息的时刻是在10时,此时离家20千米;
(3)由图象知,在10时到13时这段时间内,他们只在11时到12时运动,对应的路程差为5km;
(4)由图形可知,返回时是14时到16时,所用时间是2小时.
20.解:(1)当x=0时,y=0+2=2;
当y=0时,x+2=0,解得:x=﹣2.
描点、连线,画出函数图象,如图所示.
故答案为:2;﹣2.
(2)点A(﹣3,1)不在该函数的图象上,理由如下:
当x=﹣3时,y=﹣3+2=﹣1,﹣1≠1,
∴点A(﹣3,1)不在该函数的图象上.
21.解:(1)∵点C(﹣2,m)在直线y=﹣x+2上,
∴m=﹣(﹣2)+2=2+2=4,
∴点C(﹣2,4),
∵函数y=x+b的图象过点C(﹣2,4),
∴4=×(﹣2)+b,得b=,
即m的值是4,b的值是;
(2)①∵函数y=﹣x+2的图象与x轴,y轴分别交于点A,B,
∴点A(2,0),点B(0,2),
∵函数y=x+的图象与x轴交于点D,
∴点D的坐标为(﹣14,0),
∴AD=16,
∵△ACE的面积为12,
∴=12,
解得,t=5.
即当△ACE的面积为12时,t的值是5;
②当t=4或t=6时,△ACE是直角三角形,
理由:当∠ACE=90°时,AC⊥CE,
∵点A(2,0),点B(0,2),点C(﹣2,4),点D(﹣14,0),
∴OA=OB,AC=4,
∴∠BAO=45°,
∴∠CAE=45°,
∴∠CEA=45°,
∴CA=CE=4,
∴AE=8,
∵AE=16﹣2t,
∴8=16﹣2t,
解得,t=4;
当∠CEA=90°时,
∵AC=4,∠CAE=45°,
∴AE=4,
∵AE=16﹣2t,
∴4=16﹣2t,
解得,t=6;
由上可得,当t=4或t=6时,△ACE是直角三角形.
22.解:(1)设函数的解析式是y=kx+b,
根据题意得:,
解得:,
则函数的解析式是y=x+1;
(2)画出函数图象如图所示;
观察图象,当x≥0时,y≥1.
23.解:(1)由题意可得:y=(45﹣35)x+(8﹣5)(100﹣x)=7x+300,
∴y与x之间的函数关系式为y=7x+300;
(2)由题意可得:35x+5(100﹣x)≤2000,
解得:x≤50,
又∵x≥0,
∴0≤x≤50,
∵y=7x+300,7>0,
∴y随x的增大而增大,
∴当x=50时,可获得最大利润,最大利润为:
y=7×50+300=650(元),
100﹣x=100﹣50=50(件).
答:当购进A种商品50件,B种商品50件时,可使得A、B商品全部销售完后获得的利润最大,最大利润650元.
24.解:由题意可得:w=20(x﹣60)+25(300﹣x)+15(260﹣x)+30x=10x+10200,
∴w=10x+10200(60≤x≤260);
(2)∵w=10x+10200(60≤x≤260)
∴k=10>0,
∴w随x的增大而增大,
∴当x=60时,w有最小值为10800元,
答:从D市运往B市的救灾物资为60吨,从D市运往A市的救灾物资为200吨,从C市运往B市的救灾物资为240吨,从C市运往A市的救灾物资为0吨,此时总运费最小,最小值为10800元.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
