1.3进制转换课件(27ppt+视频)2021-2022学年浙教版(2019)高中信息技术必修1
文档属性
| 名称 | 1.3进制转换课件(27ppt+视频)2021-2022学年浙教版(2019)高中信息技术必修1 |
|
|
| 格式 | pptx | ||
| 文件大小 | 84.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2022-01-06 21:55:40 | ||
图片预览





文档简介
(共27张PPT)
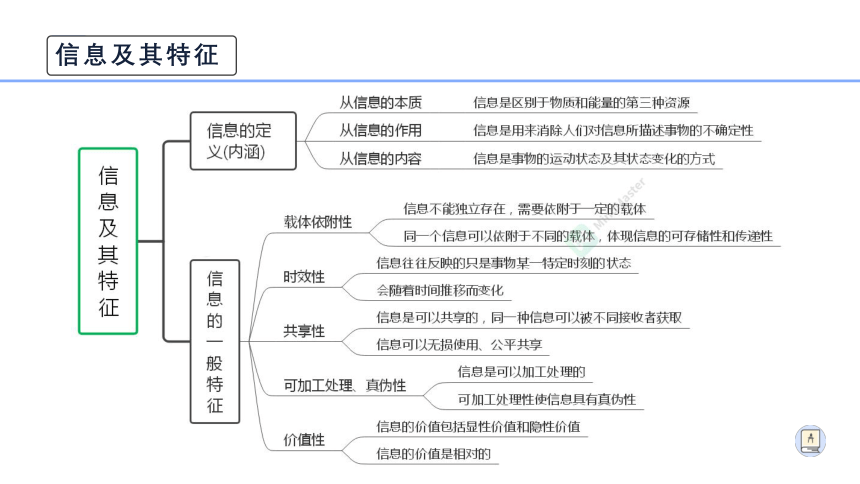
信息及其特征
信息及其特征
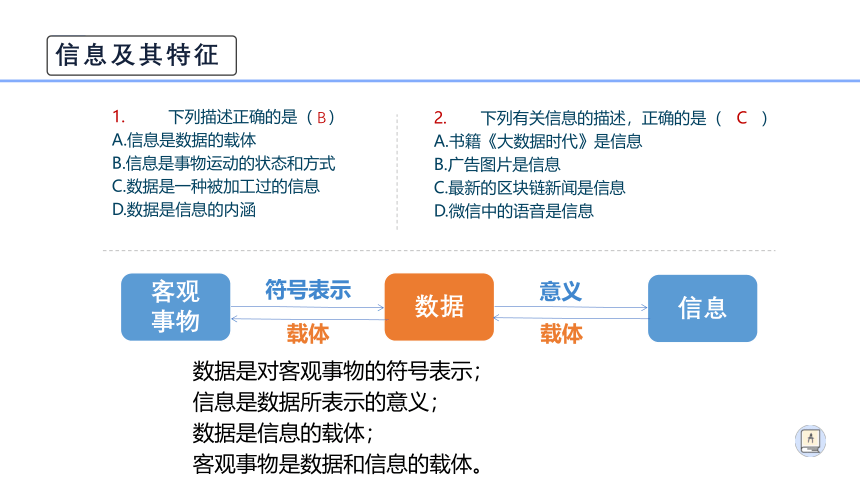
1. 下列描述正确的是( )
A.信息是数据的载体
B.信息是事物运动的状态和方式
C.数据是一种被加工过的信息
D.数据是信息的内涵
数据
信息
数据是对客观事物的符号表示;
信息是数据所表示的意义;
数据是信息的载体;
客观事物是数据和信息的载体。
2. 下列有关信息的描述,正确的是( )
A.书籍《大数据时代》是信息
B.广告图片是信息
C.最新的区块链新闻是信息
D.微信中的语音是信息
C
B
客观
事物
符号表示
意义
载体
载体
信息及其特征
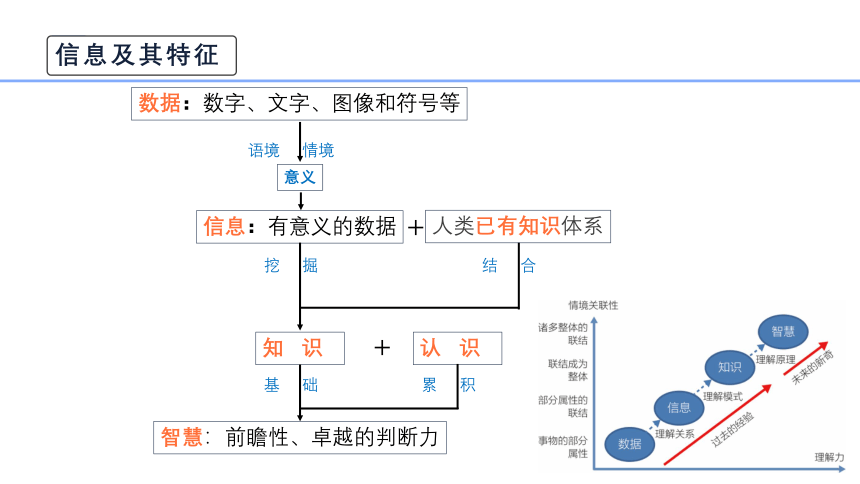
数据:数字、文字、图像和符号等
意义
语境 情境
信息:有意义的数据
挖 掘
人类已有知识体系
结 合
知 识
基 础
智慧:前瞻性、卓越的判断力
认 识
累 积
+
+
信息及其特征
2. 下列有关数据、信息和知识的说法,正确的是( )
A.数据本身具有明确的意义
B.信息只要经过挖掘就可形成知识
C.知识可以传递,但不能继承
D.不同的人加工同样的信息,最终获得的知识是不一样的
D
1. 关于数据、信息和知识,下列说法正确的有( )
A.信息和知识里不包含数据
B.信息经过提炼可以得到知识
C.数据+背景=信息
D.数据就是知识,知识就是数据
B
思考与练习
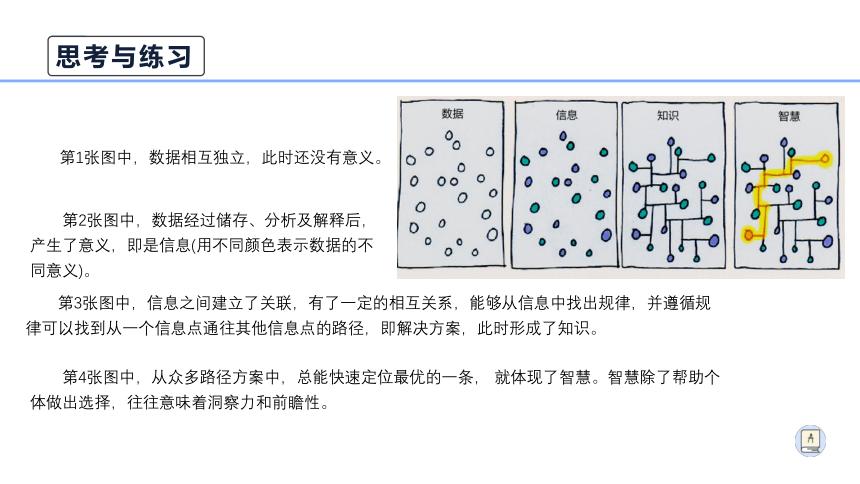
第1张图中,数据相互独立,此时还没有意义。
第2张图中,数据经过储存、分析及解释后,产生了意义,即是信息(用不同颜色表示数据的不同意义)。
第3张图中,信息之间建立了关联,有了一定的相互关系,能够从信息中找出规律,并遵循规律可以找到从一个信息点通往其他信息点的路径,即解决方案,此时形成了知识。
第4张图中,从众多路径方案中,总能快速定位最优的一条, 就体现了智慧。智慧除了帮助个体做出选择,往往意味着洞察力和前瞻性。
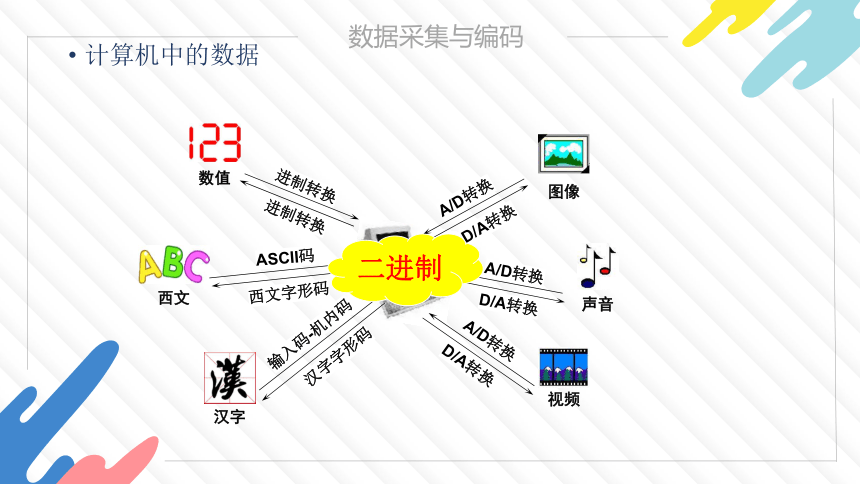
1.3数据采集
与编码
计算机中的数据
图像
声音
视频
汉字
西文
数值
进制转换
A/D转换
ASCII码
输入码-机内码
D/A转换
A/D转换
D/A转换
D/A转换
A/D转换
进制转换
西文字形码
汉字字形码
二进制
为什么要用二进制编码?
计算机作为一种电子计算工具,是由大量的电子器件组成的,在这些电子器件中,电路有两种状态的通和断。
简而言之:计算机只认识两个数字“0”和“1”。计算机处理信息的过程实质上是一个计算的过程
电路
信息
只有两种状态
各种各样
要想用电路来表示信息,就必须设计一种表示方法,使得电路的两种状态能够组合足够多的情形,以此来表示各种各样的信息。因此用“0”和“1”组成的二进制数是最合适的。
问题
问题
什么是数的进制?
生活中还有哪些记数方法?
进制是一种计数方式,亦称为进位计数法或位值计数法。
利用这种计数法,可以使用有限种数字符号来表示所有的数值。
十二进制、二十四进制、
半斤八两(旧制一斤合十六两,半斤等于八两)
(891.79)10=
8*102+9*101+1*100+7*10-1+9*10-2
0
1
位权值
十进制数
十进制数
①基(基数):组成该数制的数码个数
进制 基数 组成的数字(基本数码) 特点
十进制 10
二进制 2
十六进制 16
0,1
逢二进一
借一当二
0,1,2,3,4,5,6,7,8,9
逢十进一
借一当十
0,1,2,3,4,5,6,7,8,9
A B C D E F
逢十六进一借一当十六
进制两个基本要素:
进制两个基本要素:
②权(权值):每一个数位上1对应的数值
例:
0 * 102
2 * 101
1 * 100
+
=
2021D
+
+
2 * 103
其中的
103、
102、
101、
100
即为权值。
进制 第i位 …… 第4位 第3位 第2位 第1位 小数点
十进制 D ……
二进制 B ……
十六进制 H ……
10i-1
2i-1
16i-1
103 102 101 100
23 22 21 20
163 162 161 160
结论:
X进制的
权值为Xi-1
二进制加减法(逢二进一)
十六进制加减法(逢十六进一)
1010B-11B=
1110B+1011B=
A380H+21H=
110H-1FH=
R进制加减
例1:1101 B
方法:按权展开,相加求和
=1*20+0*21+1*22+1*23
=13 D
二进制转十进制:
练习 1000 B
=1*20+0*21+1*22+1*23
=13 D
思考:
其他进制如何转换成十进制?
其他进制转十进制:
练习:8AH=( ) D
8AH=8×161+10×160=138D
方法:按权展开,相加求和
例1: 101 H
=1*160+0*161+1*162
=13 D
结论:
X进制的
权值为Xi-1
一号篮子
1
2
4
8
二号篮子
三号篮子
四号篮子
问题
将15个苹果放入3个箱子,要取走1~15中任意个数的苹果,要求不拆开箱子。应如何装箱?
具体操作方法:
用十进制数除以2,把余数写在旁边,直到商为0, 最后把余数从下往上书写下来,即为对应的二进制数。
除2取余,倒取余数。
14D= B
十进制转换为二进制
2
14
7
3
2
2
1
2
0
…0
… 1
… 1
… 1
1110
其他进制转换为二进制
例:58D = H
58
3
0
16
16
…10
… 3
3A
方法:除R取余,倒取余数。(转几除几)
练习:128D = H
128
6
0
16
16
… 0
… 6
60
二进制转换为十六进制
添0补齐 四位一组
0 1 1 0 1 1 0 0
8 4 2 1 8 4 2 1
4+2 12
6 C
(1101100)2=( )16
6C
8421
4位二进制数对应的权值分别是8421,用这一特点可以快速计算出4位二进制所对应的十进制数或十六进制数。
例如:1101B=8+4+0+1= 13D = DH
方法:从右向左,4位变1,不足补0
十六进制转换为二进制
6 12
6=0*8+1*4+1*2+0*1 4=1*8+1*4+0*2+0*1
8 4 2 1 8 4 2 1
0 1 1 0 1 1 0 0
6CH=( )D
110110
方法:逐位分解,一位变四,不足补0
数码范围:
0,1,2……R-1
n位R进制数表示数范围:
0——Rn-1
111111B
31
32
127D=( ) B
R进制数规律
1111111
问题
某7位二进制数的最高位为1,将其转换为十进制数的取值范围为多少
【64,128)
进制 表示方式 基数 数码 权值 进位规则
十进制 D 10 0,1,2,3,4,5,6,7,8,9 10n 逢十进一
二进制 B 2 0,1 2n 逢二进一
八进制 O 8 0,1,2,3,4,5,6,7 8n 逢八进一
十六进制 H 16 0,1,2,3,4,5,6,7,8,9 A,B,C,D,E,F 16n 逢十六进一
课后小结
R进制转十进制
1
3
4
2
按权展开,相加求和
十进制转R进制
除R取余,倒取余数
二进制转十六进制
4位变1,不足补0
十六进制转二进制
按权展开,相加求和
课后小结
信息及其特征
信息及其特征
1. 下列描述正确的是( )
A.信息是数据的载体
B.信息是事物运动的状态和方式
C.数据是一种被加工过的信息
D.数据是信息的内涵
数据
信息
数据是对客观事物的符号表示;
信息是数据所表示的意义;
数据是信息的载体;
客观事物是数据和信息的载体。
2. 下列有关信息的描述,正确的是( )
A.书籍《大数据时代》是信息
B.广告图片是信息
C.最新的区块链新闻是信息
D.微信中的语音是信息
C
B
客观
事物
符号表示
意义
载体
载体
信息及其特征
数据:数字、文字、图像和符号等
意义
语境 情境
信息:有意义的数据
挖 掘
人类已有知识体系
结 合
知 识
基 础
智慧:前瞻性、卓越的判断力
认 识
累 积
+
+
信息及其特征
2. 下列有关数据、信息和知识的说法,正确的是( )
A.数据本身具有明确的意义
B.信息只要经过挖掘就可形成知识
C.知识可以传递,但不能继承
D.不同的人加工同样的信息,最终获得的知识是不一样的
D
1. 关于数据、信息和知识,下列说法正确的有( )
A.信息和知识里不包含数据
B.信息经过提炼可以得到知识
C.数据+背景=信息
D.数据就是知识,知识就是数据
B
思考与练习
第1张图中,数据相互独立,此时还没有意义。
第2张图中,数据经过储存、分析及解释后,产生了意义,即是信息(用不同颜色表示数据的不同意义)。
第3张图中,信息之间建立了关联,有了一定的相互关系,能够从信息中找出规律,并遵循规律可以找到从一个信息点通往其他信息点的路径,即解决方案,此时形成了知识。
第4张图中,从众多路径方案中,总能快速定位最优的一条, 就体现了智慧。智慧除了帮助个体做出选择,往往意味着洞察力和前瞻性。
1.3数据采集
与编码
计算机中的数据
图像
声音
视频
汉字
西文
数值
进制转换
A/D转换
ASCII码
输入码-机内码
D/A转换
A/D转换
D/A转换
D/A转换
A/D转换
进制转换
西文字形码
汉字字形码
二进制
为什么要用二进制编码?
计算机作为一种电子计算工具,是由大量的电子器件组成的,在这些电子器件中,电路有两种状态的通和断。
简而言之:计算机只认识两个数字“0”和“1”。计算机处理信息的过程实质上是一个计算的过程
电路
信息
只有两种状态
各种各样
要想用电路来表示信息,就必须设计一种表示方法,使得电路的两种状态能够组合足够多的情形,以此来表示各种各样的信息。因此用“0”和“1”组成的二进制数是最合适的。
问题
问题
什么是数的进制?
生活中还有哪些记数方法?
进制是一种计数方式,亦称为进位计数法或位值计数法。
利用这种计数法,可以使用有限种数字符号来表示所有的数值。
十二进制、二十四进制、
半斤八两(旧制一斤合十六两,半斤等于八两)
(891.79)10=
8*102+9*101+1*100+7*10-1+9*10-2
0
1
位权值
十进制数
十进制数
①基(基数):组成该数制的数码个数
进制 基数 组成的数字(基本数码) 特点
十进制 10
二进制 2
十六进制 16
0,1
逢二进一
借一当二
0,1,2,3,4,5,6,7,8,9
逢十进一
借一当十
0,1,2,3,4,5,6,7,8,9
A B C D E F
逢十六进一借一当十六
进制两个基本要素:
进制两个基本要素:
②权(权值):每一个数位上1对应的数值
例:
0 * 102
2 * 101
1 * 100
+
=
2021D
+
+
2 * 103
其中的
103、
102、
101、
100
即为权值。
进制 第i位 …… 第4位 第3位 第2位 第1位 小数点
十进制 D ……
二进制 B ……
十六进制 H ……
10i-1
2i-1
16i-1
103 102 101 100
23 22 21 20
163 162 161 160
结论:
X进制的
权值为Xi-1
二进制加减法(逢二进一)
十六进制加减法(逢十六进一)
1010B-11B=
1110B+1011B=
A380H+21H=
110H-1FH=
R进制加减
例1:1101 B
方法:按权展开,相加求和
=1*20+0*21+1*22+1*23
=13 D
二进制转十进制:
练习 1000 B
=1*20+0*21+1*22+1*23
=13 D
思考:
其他进制如何转换成十进制?
其他进制转十进制:
练习:8AH=( ) D
8AH=8×161+10×160=138D
方法:按权展开,相加求和
例1: 101 H
=1*160+0*161+1*162
=13 D
结论:
X进制的
权值为Xi-1
一号篮子
1
2
4
8
二号篮子
三号篮子
四号篮子
问题
将15个苹果放入3个箱子,要取走1~15中任意个数的苹果,要求不拆开箱子。应如何装箱?
具体操作方法:
用十进制数除以2,把余数写在旁边,直到商为0, 最后把余数从下往上书写下来,即为对应的二进制数。
除2取余,倒取余数。
14D= B
十进制转换为二进制
2
14
7
3
2
2
1
2
0
…0
… 1
… 1
… 1
1110
其他进制转换为二进制
例:58D = H
58
3
0
16
16
…10
… 3
3A
方法:除R取余,倒取余数。(转几除几)
练习:128D = H
128
6
0
16
16
… 0
… 6
60
二进制转换为十六进制
添0补齐 四位一组
0 1 1 0 1 1 0 0
8 4 2 1 8 4 2 1
4+2 12
6 C
(1101100)2=( )16
6C
8421
4位二进制数对应的权值分别是8421,用这一特点可以快速计算出4位二进制所对应的十进制数或十六进制数。
例如:1101B=8+4+0+1= 13D = DH
方法:从右向左,4位变1,不足补0
十六进制转换为二进制
6 12
6=0*8+1*4+1*2+0*1 4=1*8+1*4+0*2+0*1
8 4 2 1 8 4 2 1
0 1 1 0 1 1 0 0
6CH=( )D
110110
方法:逐位分解,一位变四,不足补0
数码范围:
0,1,2……R-1
n位R进制数表示数范围:
0——Rn-1
111111B
31
32
127D=( ) B
R进制数规律
1111111
问题
某7位二进制数的最高位为1,将其转换为十进制数的取值范围为多少
【64,128)
进制 表示方式 基数 数码 权值 进位规则
十进制 D 10 0,1,2,3,4,5,6,7,8,9 10n 逢十进一
二进制 B 2 0,1 2n 逢二进一
八进制 O 8 0,1,2,3,4,5,6,7 8n 逢八进一
十六进制 H 16 0,1,2,3,4,5,6,7,8,9 A,B,C,D,E,F 16n 逢十六进一
课后小结
R进制转十进制
1
3
4
2
按权展开,相加求和
十进制转R进制
除R取余,倒取余数
二进制转十六进制
4位变1,不足补0
十六进制转二进制
按权展开,相加求和
课后小结
