2021—2022学年人浙教版数学八年级上册2.3等腰三角形的性质定理(2)(共14张ppt)
文档属性
| 名称 | 2021—2022学年人浙教版数学八年级上册2.3等腰三角形的性质定理(2)(共14张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 574.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-09 07:47:26 | ||
图片预览



文档简介
(共14张PPT)
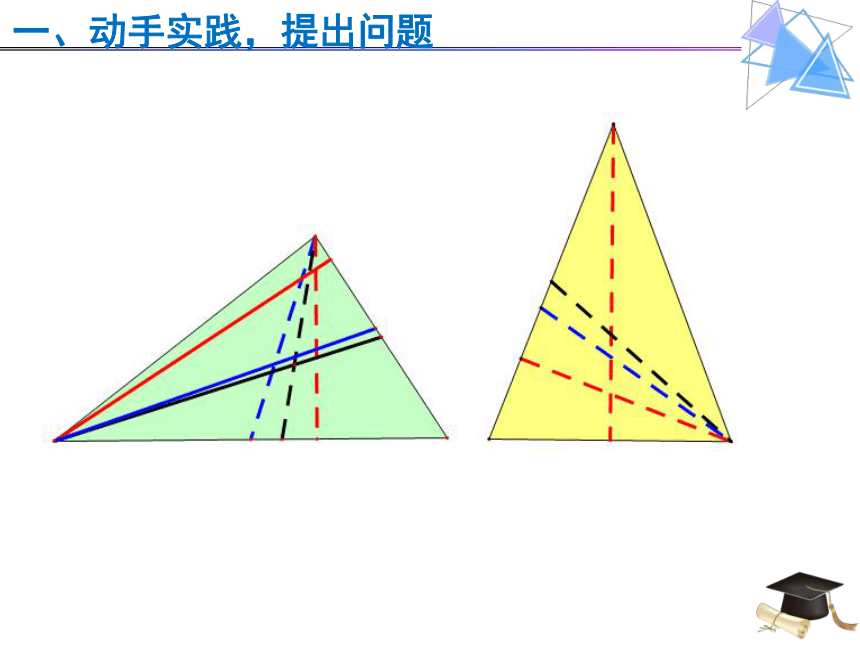
一、动手实践,提出问题
小组合作:
1.每人选一张三角形纸片;
2.画出三角形纸片任意两边上的中线、高线及其所对角的角平分线;(画图工具、方法不限)
3.组内交流汇总.
一、动手实践,提出问题
浙江教育出版社八年级【上】数学
2.3等腰三角形的性质定理(2)
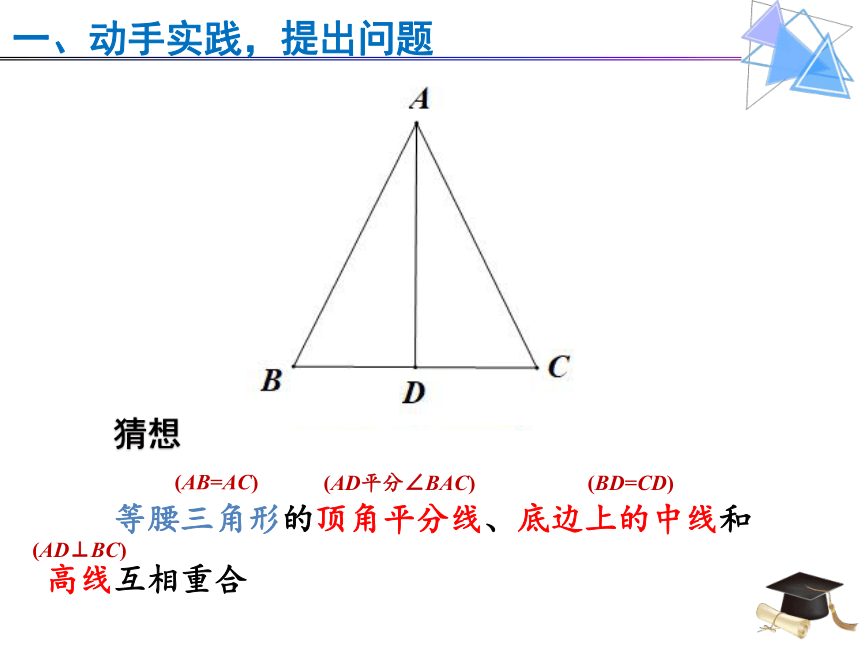
一、动手实践,提出问题
等腰三角形的顶角平分线、底边上的中线和高线互相重合
猜想
(AB=AC)
(AD平分∠BAC)
(BD=CD)
(AD⊥BC)
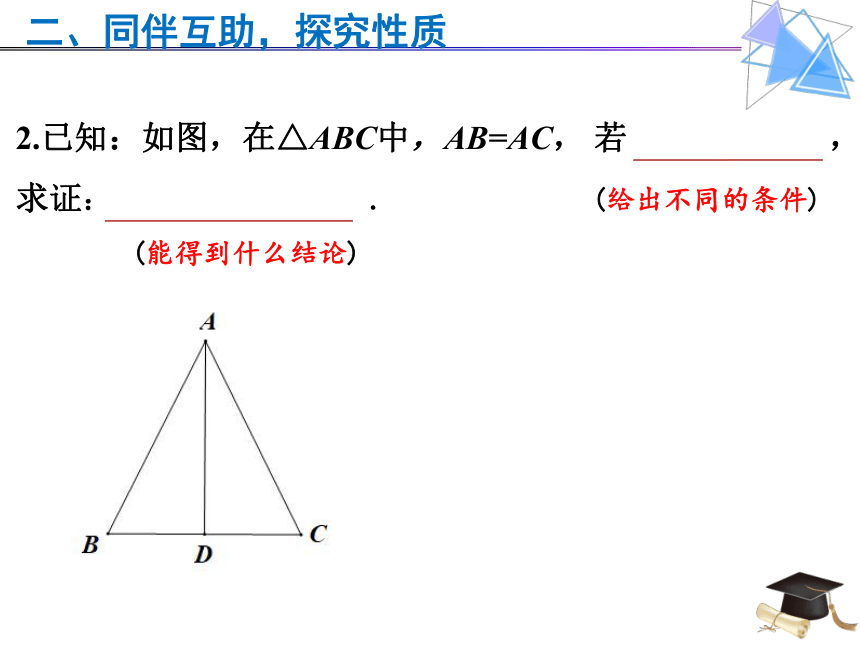
二、同伴互助,探究性质
2.已知:如图,在△ABC中,AB=AC, 若 ,
求证: . (给出不同的条件)
(能得到什么结论)
三、师生合作,得出定理
等腰三角形的性质定理2:
等腰三角形的顶角平分线、底边上的中线和高线互相重合,简称等腰三角形三线合一。
几何语言:
(1)∵AB=AC,AD平分∠BAC,
∴AD⊥BC,BD=CD.
(2)∵AB=AC,BD=CD,
∴AD平分∠BAC,AD⊥BC.
(3)∵AB=AC,AD⊥BC,
∴AD平分∠BAC,BD=CD.
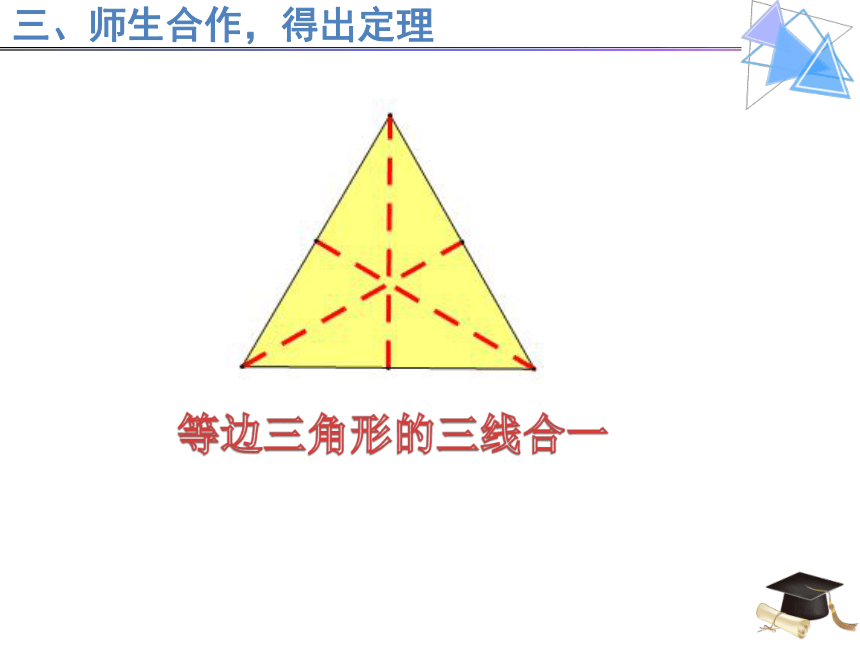
三、师生合作,得出定理
等边三角形的三线合一
四、学以致用,巩固新知
10
练习1:
如图,在△ABC中,AB=AC.
(1)若AD平分∠BAC,BD=4, 则CD= .
(2)若BD=CD,∠BAC=100°,则∠CAD= .
(3)若AD⊥BC于点D,CD=5,则BC= .
50°
4
五、性质应用,提升能力
例1: 如图,已知点D在△ABC 的内部,连结AD、BD、CD,若AD平分∠BAC,∠ADB=∠ADC,求证:AD⊥BC.
证明:如图,延长AD,交BC于点E
∵AD平分∠BAC,∴∠BAD=∠CAD
∵AD=AD,∠ADB=∠ADC
∴ △ABD ≌ △ACD (ASA)
∴AB=AC
∵AE平分∠BAC
∴AE⊥BC
即AD⊥BC(等腰三角形的三线合一)
练习2: 如图,已知AD是△ABC 的角平分线,DE ⊥AB于点E, DF ⊥AC于点F ,BE=CF,求证:AD垂直平分BC.
五、性质应用,提升能力
例2:如图,已知线段a,h,用直尺和圆规作等腰三角形ABC,使底边BC=a,底边BC上的高线长为h.
作法:
1.作线段BC=a;
2.作线段BC的垂直平分线l,交BC于点D;
3.在直线l上截取DA=h,连结AB,AC.
△ABC就是所求的等腰三角形.
五、性质应用,提升能力
在古代,建筑工人用一把等腰三角形尺和悬挂在顶点处的重锤线自制水准仪,用来检查一根横梁是否水平。检查时,将三角形的底边紧靠栋梁,如果重锤线经过底边的中点,就说明横梁是水平的。
生
活
中
的
数
学
六、联系实际,突出应用
七、归纳小结,明晰过程
探究过程
探究方法
等腰三角形三线合一
提出问题
同伴互助
师生合作
计算
证明
作图
实践
操作发现
得出结论
推理验证
命题猜想
1.必做题
作业本:2.3等腰三角形的性质定理(2)
2.选做题
(1)制作一个简单的水准仪
(2)以长方形一边为底边,只用直尺画出一个等腰三角形,并简要说明理由.
作业布置
一、动手实践,提出问题
小组合作:
1.每人选一张三角形纸片;
2.画出三角形纸片任意两边上的中线、高线及其所对角的角平分线;(画图工具、方法不限)
3.组内交流汇总.
一、动手实践,提出问题
浙江教育出版社八年级【上】数学
2.3等腰三角形的性质定理(2)
一、动手实践,提出问题
等腰三角形的顶角平分线、底边上的中线和高线互相重合
猜想
(AB=AC)
(AD平分∠BAC)
(BD=CD)
(AD⊥BC)
二、同伴互助,探究性质
2.已知:如图,在△ABC中,AB=AC, 若 ,
求证: . (给出不同的条件)
(能得到什么结论)
三、师生合作,得出定理
等腰三角形的性质定理2:
等腰三角形的顶角平分线、底边上的中线和高线互相重合,简称等腰三角形三线合一。
几何语言:
(1)∵AB=AC,AD平分∠BAC,
∴AD⊥BC,BD=CD.
(2)∵AB=AC,BD=CD,
∴AD平分∠BAC,AD⊥BC.
(3)∵AB=AC,AD⊥BC,
∴AD平分∠BAC,BD=CD.
三、师生合作,得出定理
等边三角形的三线合一
四、学以致用,巩固新知
10
练习1:
如图,在△ABC中,AB=AC.
(1)若AD平分∠BAC,BD=4, 则CD= .
(2)若BD=CD,∠BAC=100°,则∠CAD= .
(3)若AD⊥BC于点D,CD=5,则BC= .
50°
4
五、性质应用,提升能力
例1: 如图,已知点D在△ABC 的内部,连结AD、BD、CD,若AD平分∠BAC,∠ADB=∠ADC,求证:AD⊥BC.
证明:如图,延长AD,交BC于点E
∵AD平分∠BAC,∴∠BAD=∠CAD
∵AD=AD,∠ADB=∠ADC
∴ △ABD ≌ △ACD (ASA)
∴AB=AC
∵AE平分∠BAC
∴AE⊥BC
即AD⊥BC(等腰三角形的三线合一)
练习2: 如图,已知AD是△ABC 的角平分线,DE ⊥AB于点E, DF ⊥AC于点F ,BE=CF,求证:AD垂直平分BC.
五、性质应用,提升能力
例2:如图,已知线段a,h,用直尺和圆规作等腰三角形ABC,使底边BC=a,底边BC上的高线长为h.
作法:
1.作线段BC=a;
2.作线段BC的垂直平分线l,交BC于点D;
3.在直线l上截取DA=h,连结AB,AC.
△ABC就是所求的等腰三角形.
五、性质应用,提升能力
在古代,建筑工人用一把等腰三角形尺和悬挂在顶点处的重锤线自制水准仪,用来检查一根横梁是否水平。检查时,将三角形的底边紧靠栋梁,如果重锤线经过底边的中点,就说明横梁是水平的。
生
活
中
的
数
学
六、联系实际,突出应用
七、归纳小结,明晰过程
探究过程
探究方法
等腰三角形三线合一
提出问题
同伴互助
师生合作
计算
证明
作图
实践
操作发现
得出结论
推理验证
命题猜想
1.必做题
作业本:2.3等腰三角形的性质定理(2)
2.选做题
(1)制作一个简单的水准仪
(2)以长方形一边为底边,只用直尺画出一个等腰三角形,并简要说明理由.
作业布置
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
