3.1用计算机解决问题的一般过程现课件(15ppt)2021-2022学年浙教版(2019)高中信息技术必修1《数据与计算》
文档属性
| 名称 | 3.1用计算机解决问题的一般过程现课件(15ppt)2021-2022学年浙教版(2019)高中信息技术必修1《数据与计算》 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2022-01-12 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
3.1用计算机解决问题的一般过程
一、算法和程序
先有算法还是先有程序?
程序是算法的一种描述方式——先有算法后有程序。
二、用计算机解决问题的一般过程
问题思考:用计算机绘制正多边形(正多边形的各边边长相等,各内角度数也相等)
用计算机绘制
寻找现有软件:WORD\PS\FLASH\画图工具
如需绘制多个正多边形,考虑用计算机编程自动完成。
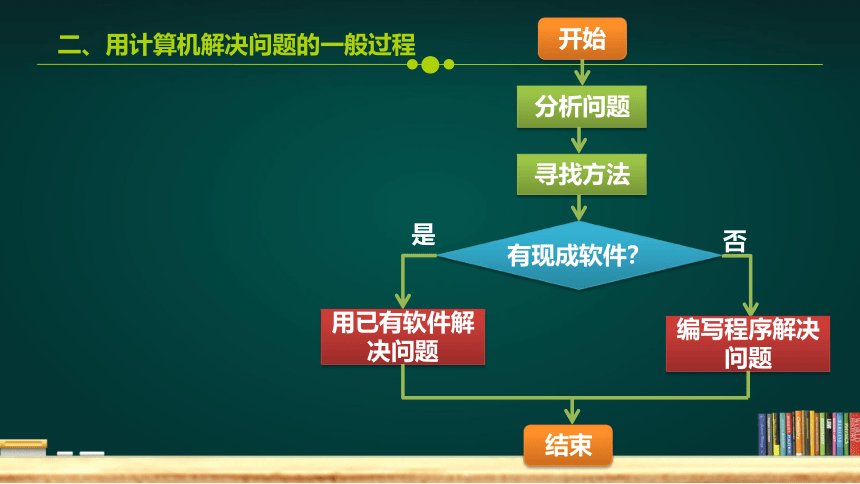
二、用计算机解决问题的一般过程
开始
分析问题
寻找方法
有现成软件?
用已有软件解决问题
编写程序解决问题
结束
是
否
三、用计算机编程解决问题的一般过程
问题思考:用计算机编程绘制正多边形(正多边形的各边边长相等,各内角度数也相等)
1.抽象与建模
正多边形的各边边长相等,各内角度数也相等。因此,绘制一个正多边形,可以通过“画一条边,旋转一定角度后再画一条边”的重复操作来完成。下图呈现的是绘制一个正六边形的过程。
提炼核心要素
三、用计算机编程解决问题的一般过程
1.抽象与建模
绘制正多边形,除了要知道它的边数n和边长a,关键是要计算出每次旋转的角度。因此,解决这个问题的计算模型可以表示如下:
假设正多边形的边数为n, 边长为a。
则内角度数d的值为:d= (n-2) x180+n。
每次旋转的角度为:180-d。
建立数学模型
三、用计算机编程解决问题的一般过程
2.设计算法
基于问题的抽象与建模,绘制一个正多边形的算法可以做如下描述:
①输人要绘制的正多边形的边数n和边长a。
②计算正多边形的每个内角度数d, 其中d= (n-2) x180÷n。
③将以下过程重复执行n遍:画一条长度为a的线段,再将画笔方向向左(逆时针)旋转(180-d) 度。
输入数据
处理数据
输出数据
三、用计算机编程解决问题的一般过程
3.编写程序
要让计算机按照预先设计的算法进行处理,需要将该算法用计算机程序设计语言描述,形成计算机程序。用Python语言描述绘制正多边形的算法:
import turtle
n=int (input ("please input n: "))
a=int (input ("please input a: "))
d= (n-2)*180/n
t=turtle. Pen()
for i in range(n) : #重复执行n遍
t.forward(a) #向前绘制长度为a的线段
t.left(180-d) #向左旋转(180-d) 度
四、项目拓展与实践
绘制如图的五角星
一、抽象建模
二、设计算法
三、编写程序
四、调试运行程序
提炼核心要素
建立数学模型
输入数据
处理数据
输出数据
三、用计算机编程解决问题的一般过程
4.调试运行程序
通过运行程序,计算机会自动执行程序中的命令。但是,在将算法进行程序实现时,可能会因为录入错误、语法错误、逻辑错误等原因,导致程序不能正常运行或输出错误的结果。此时,需要对程序进行调试,以便发现错误并进行修正。例如、字母大小写的疏忽可能直接决定程序能否正常运行,程序中参数的调整可能影响输出图形的形状。
五、拓展与实践
世界近代三大数学难题之一。哥德巴赫是德国一位中学教师,也是一位数学家,生于1690年,1725年当选为俄国彼得堡科学院院士。1742年,哥德巴赫在教学中发现,每个不小于6的偶数都是两个素数(只能被1和它本身整除的数)之和。如6=3+3,12=5+7等。
公元1742年6月7日哥德巴赫(Goldbach)写信给大数学家欧拉(Euler),提出了以下的猜想:
(a) 任何一个>=6之偶数,都可以表示成两个奇质数之和。
(b) 任何一个>=9之奇数,都可以表示成三个奇质数之和。
这就是着名的哥德巴赫猜想。
目前最佳的结果是中国数学家陈景润于1966年证明的,称为“陈氏定理“ 。任何充分大的偶数都是一个质数与一个自然数之和,而后者仅仅是两个质数的乘积。” 通常都简称这个结果为大偶数可表示为 ”1 + 2 “的形式。
五、拓展与实践
四、思考与实践
请试着描述用计算机编程验证“哥德巴赫猜想”的一般过程
按小组讨论,四步走,展示成果。
抽象与建模
用计算机编程解决问题的一般过程
设计算法
调试运行程序
编写程序
提炼核心要素
建立数学模型
输入数据
处理数据
输出数据
Thank You
3.1用计算机解决问题的一般过程
一、算法和程序
先有算法还是先有程序?
程序是算法的一种描述方式——先有算法后有程序。
二、用计算机解决问题的一般过程
问题思考:用计算机绘制正多边形(正多边形的各边边长相等,各内角度数也相等)
用计算机绘制
寻找现有软件:WORD\PS\FLASH\画图工具
如需绘制多个正多边形,考虑用计算机编程自动完成。
二、用计算机解决问题的一般过程
开始
分析问题
寻找方法
有现成软件?
用已有软件解决问题
编写程序解决问题
结束
是
否
三、用计算机编程解决问题的一般过程
问题思考:用计算机编程绘制正多边形(正多边形的各边边长相等,各内角度数也相等)
1.抽象与建模
正多边形的各边边长相等,各内角度数也相等。因此,绘制一个正多边形,可以通过“画一条边,旋转一定角度后再画一条边”的重复操作来完成。下图呈现的是绘制一个正六边形的过程。
提炼核心要素
三、用计算机编程解决问题的一般过程
1.抽象与建模
绘制正多边形,除了要知道它的边数n和边长a,关键是要计算出每次旋转的角度。因此,解决这个问题的计算模型可以表示如下:
假设正多边形的边数为n, 边长为a。
则内角度数d的值为:d= (n-2) x180+n。
每次旋转的角度为:180-d。
建立数学模型
三、用计算机编程解决问题的一般过程
2.设计算法
基于问题的抽象与建模,绘制一个正多边形的算法可以做如下描述:
①输人要绘制的正多边形的边数n和边长a。
②计算正多边形的每个内角度数d, 其中d= (n-2) x180÷n。
③将以下过程重复执行n遍:画一条长度为a的线段,再将画笔方向向左(逆时针)旋转(180-d) 度。
输入数据
处理数据
输出数据
三、用计算机编程解决问题的一般过程
3.编写程序
要让计算机按照预先设计的算法进行处理,需要将该算法用计算机程序设计语言描述,形成计算机程序。用Python语言描述绘制正多边形的算法:
import turtle
n=int (input ("please input n: "))
a=int (input ("please input a: "))
d= (n-2)*180/n
t=turtle. Pen()
for i in range(n) : #重复执行n遍
t.forward(a) #向前绘制长度为a的线段
t.left(180-d) #向左旋转(180-d) 度
四、项目拓展与实践
绘制如图的五角星
一、抽象建模
二、设计算法
三、编写程序
四、调试运行程序
提炼核心要素
建立数学模型
输入数据
处理数据
输出数据
三、用计算机编程解决问题的一般过程
4.调试运行程序
通过运行程序,计算机会自动执行程序中的命令。但是,在将算法进行程序实现时,可能会因为录入错误、语法错误、逻辑错误等原因,导致程序不能正常运行或输出错误的结果。此时,需要对程序进行调试,以便发现错误并进行修正。例如、字母大小写的疏忽可能直接决定程序能否正常运行,程序中参数的调整可能影响输出图形的形状。
五、拓展与实践
世界近代三大数学难题之一。哥德巴赫是德国一位中学教师,也是一位数学家,生于1690年,1725年当选为俄国彼得堡科学院院士。1742年,哥德巴赫在教学中发现,每个不小于6的偶数都是两个素数(只能被1和它本身整除的数)之和。如6=3+3,12=5+7等。
公元1742年6月7日哥德巴赫(Goldbach)写信给大数学家欧拉(Euler),提出了以下的猜想:
(a) 任何一个>=6之偶数,都可以表示成两个奇质数之和。
(b) 任何一个>=9之奇数,都可以表示成三个奇质数之和。
这就是着名的哥德巴赫猜想。
目前最佳的结果是中国数学家陈景润于1966年证明的,称为“陈氏定理“ 。任何充分大的偶数都是一个质数与一个自然数之和,而后者仅仅是两个质数的乘积。” 通常都简称这个结果为大偶数可表示为 ”1 + 2 “的形式。
五、拓展与实践
四、思考与实践
请试着描述用计算机编程验证“哥德巴赫猜想”的一般过程
按小组讨论,四步走,展示成果。
抽象与建模
用计算机编程解决问题的一般过程
设计算法
调试运行程序
编写程序
提炼核心要素
建立数学模型
输入数据
处理数据
输出数据
Thank You
