探求二次函数图象和系数的关系

课件8张PPT。探究二次函数图像位置与系数的关系龙游华茂外国语学校

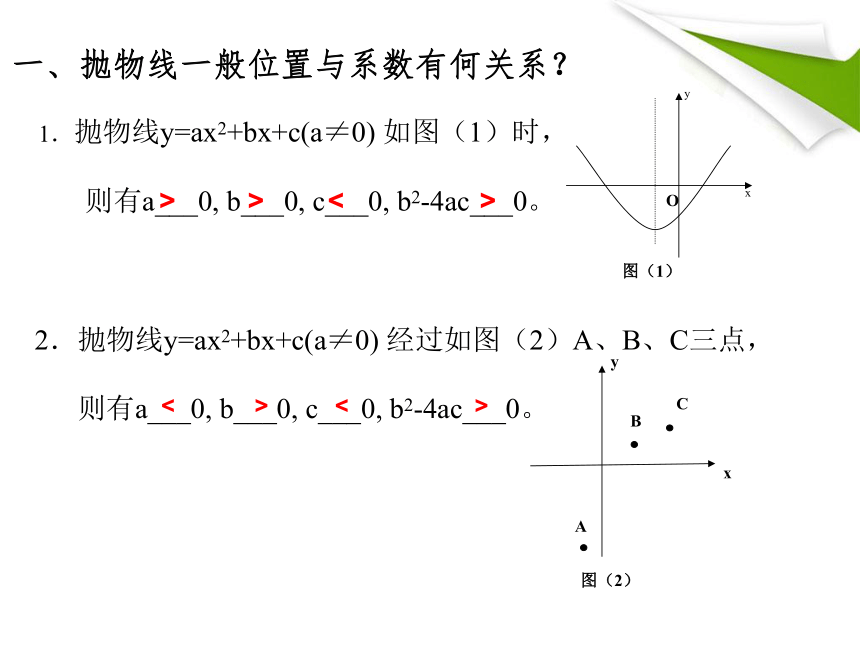
吴文军一、抛物线一般位置与系数有何关系？ 1．抛物线y=ax2+bx+c(a≠0) 如图（1）时，
则有a___0, b___0, c___0, b2-4ac___0。
2．抛物线y=ax2+bx+c(a≠0) 经过如图（2）A、B、C三点，
则有a___0, b___0, c___0, b2-4ac___0。
> > < >< > < >
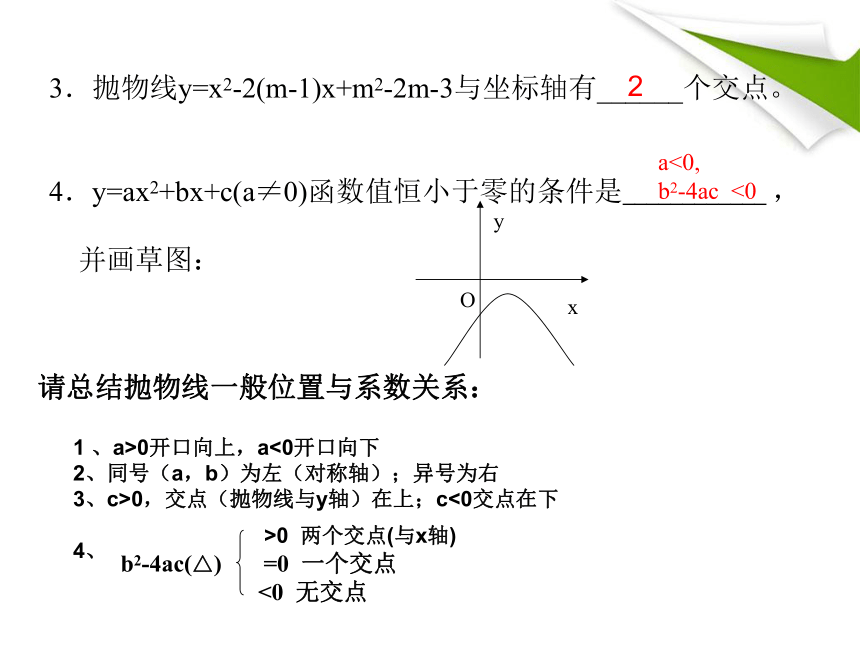
3．抛物线y=x2-2(m-1)x+m2-2m-3与坐标轴有______个交点。
4．y=ax2+bx+c(a≠0)函数值恒小于零的条件是____________ ，
并画草图：
请总结抛物线一般位置与系数关系：1 、a>0开口向上，a<0开口向下
2、同号（a，b）为左（对称轴）；异号为右
3、c>0，交点（抛物线与y轴）在上；c<0交点在下
4、2a<0,
b2-4ac <0 二、抛物线特殊位置时与系数有何关系？
1．抛物线y=ax2+bx+c(a≠0) 位置分别如下列四图时，其系数中
的特殊值对应的分别有
特殊值：

_________ _________ __________ __________
2．抛物线y=x2-2kx+k2+k过原点，则k= _____c=0 b2-4ac =0 b=0 b=c=00,-1
3．抛物线y=(k+1)x2+(k2-1)x-1的顶点在y轴上，则k=______。
4．若y关于x的函数y=(a-2)x2-(2a-1)x+a的图像与坐标轴有两个交
点，则a的取值为__________。
请总结抛物线特殊位置与系数的关系： 11、c=0 过原点
2、b2-4ac =0 与x轴一个交点
3、b=0 顶点（对称轴）y轴
4、b=c=0 顶点在原点三、有特定点时抛物线的位置与系数关系如何确定？ 1．抛物线y=ax2+bx+c(a≠0)图像如图，

则有a+b+c___0, a+c___b, 4a+2b+c___0,
(a+c)2___b2。
2．抛物线y=ax2+bx+c(a≠0)如右图，且经过A(1,0), B(3,0)，
则有a___0, b___0, c___0, 4a+b___0。
< > >
< < > < =3．抛物线y=ax2+bx+c(a≠0) 图像如图，则有
a+b+c___am2+bm+c(m≠1), 2a+b___0,4a+2b+c____0,
9a+3b+c___0, 2c—3b____0。
> = >

< <请总结抛物线有特定点时，
确定系数关系式的方法。思想方法：代入 重组谢谢指导