1.1 二次根式 精品课件(共26张PPT)
文档属性
| 名称 | 1.1 二次根式 精品课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-17 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
1.1二次根式
浙教版 八年级下
新知导入
a(a≥0)的平方根是 .
算术平方根是 .
课前回顾
正数有两个平方根且互为相反数;
0有一个平方根就是0;
负数没有平方根.
平方根的性质:
新知导入
根据下图所示的直角三角形、正方形和等边三角形的条件,完成以下填空:
2cm
a cm
直角三角形的边长是: .
新知探究
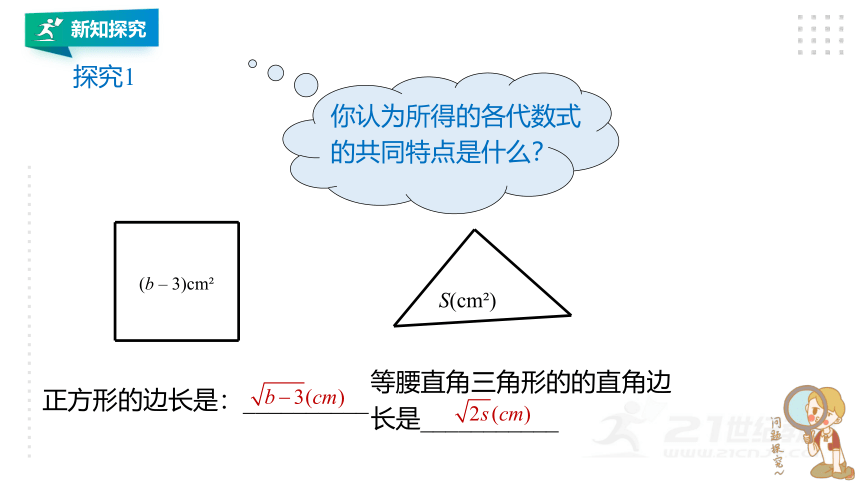
(b – 3)cm
正方形的边长是:__________
探究1
S(cm )
等腰直角三角形的的直角边长是___________
你认为所得的各代数式的共同特点是什么?
新知探究
的共同特点:
表示的是算术平方根
根号内含有字母的代数式
归纳
新知探究
为了方便起见,我们把一个数的算术平方根也叫二次根式.
例如: , 也叫二次根式.
总结
像 这样表示的是算术平方根,且根号内含有字母的代数式叫二次根式.
新知讲解
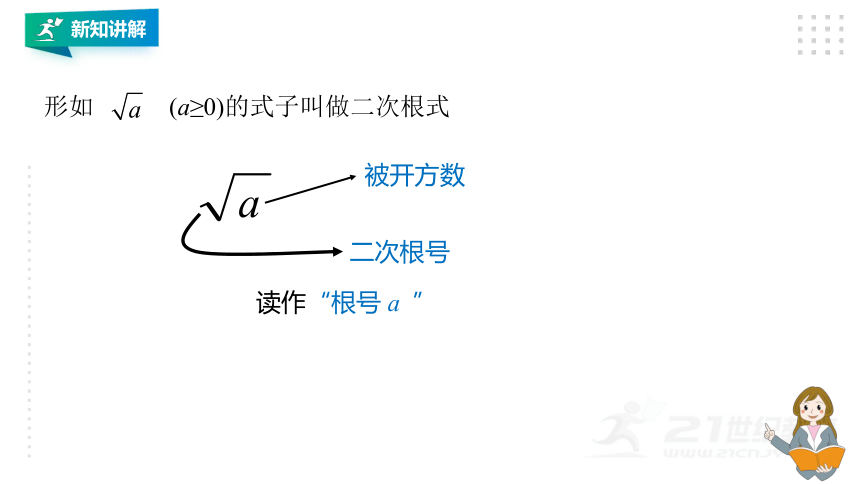
被开方数
二次根号
读作“根号 a ”
形如 (a≥0)的式子叫做二次根式
下列各式中哪些是二次根式?
新知落实
例题讲解
例1:a取何值时,下列根式有意义?
解:(1)∵a+1≥0,解得a≥-1
探究2
举一反三
变式
a取何值时,下列根式有意义?
举一反三:
课堂练习
求下列二次根式中字母的取值范围:
(1) (2)
(1)解: 由题意得,
(2)解: 由题意得,
课堂练习
(4)解: 由题意得,
(3)解: 由题意得,
归纳总结
求二次根式中字母的取值范围的基本依据:
①被开方数大于等于零;
②分母中有字母时,要保证分母不为零.
③多个条件组合时,应用不等式组求解
例2:当x=-4时,求二次根式 的值.
解:将x=-4代入二次根式,得
例题讲解
若二次根式 的值为3,求 x 的值.
解:由题意得:
两边同时平方得:
例3:已知 +|3b-9|+(4-c)2=0,求 2a-b+c 的值.
解: ∵ ≥0,|3b-9|≥0,(4-c) 2≥0,
又∵ +|3b-9|+(4-c) 2=0 ,
∴a+2=0 , 3b-9=0 , 4-c=0.
∴a= -2 , b= 3 ,c= 4
∴2a-b+c=2×(-2) -3+4 = -3.
例题讲解
若a,b为实数 ,且
求 的值.
解:
课堂总结
1、二次根式的概念.
2、根号内字母的取值范围.
今天我们学习了哪些知识?
1. 下列各式是二次根式吗
是
不是
不是
是
是
是
不是
不是
不是
不是
课堂练习
2. x取何值时,下列二次根式有意义?
4、若二次根式 的值为3,求x的值
3、当x=-2时,求二次根式 的值
提示:x=3或x=-3
提示:值为1
5. 已知
,求 的值.
解: 由题意得,
6. 一艘轮船先向东北方向航行2小时,再向西北方向航行t小时,船的航速是每时25千米.
(1) 用关于t的代数式表示船离开出发地的距离.
(2) 求当t=3时,船离开出发地多少千米.(精确到0.01)
东
北
解: (1)设船离出发地的距离为s千米
45°
45°
45°
(2)当t=3时
答:当t=3时,船离开出发地90.14千米.
1.作业本1 2.3有理数的乘法(1)
2.自主练习
作业布置
https://www.21cnjy.com/help/help_extract.php
1.1二次根式
浙教版 八年级下
新知导入
a(a≥0)的平方根是 .
算术平方根是 .
课前回顾
正数有两个平方根且互为相反数;
0有一个平方根就是0;
负数没有平方根.
平方根的性质:
新知导入
根据下图所示的直角三角形、正方形和等边三角形的条件,完成以下填空:
2cm
a cm
直角三角形的边长是: .
新知探究
(b – 3)cm
正方形的边长是:__________
探究1
S(cm )
等腰直角三角形的的直角边长是___________
你认为所得的各代数式的共同特点是什么?
新知探究
的共同特点:
表示的是算术平方根
根号内含有字母的代数式
归纳
新知探究
为了方便起见,我们把一个数的算术平方根也叫二次根式.
例如: , 也叫二次根式.
总结
像 这样表示的是算术平方根,且根号内含有字母的代数式叫二次根式.
新知讲解
被开方数
二次根号
读作“根号 a ”
形如 (a≥0)的式子叫做二次根式
下列各式中哪些是二次根式?
新知落实
例题讲解
例1:a取何值时,下列根式有意义?
解:(1)∵a+1≥0,解得a≥-1
探究2
举一反三
变式
a取何值时,下列根式有意义?
举一反三:
课堂练习
求下列二次根式中字母的取值范围:
(1) (2)
(1)解: 由题意得,
(2)解: 由题意得,
课堂练习
(4)解: 由题意得,
(3)解: 由题意得,
归纳总结
求二次根式中字母的取值范围的基本依据:
①被开方数大于等于零;
②分母中有字母时,要保证分母不为零.
③多个条件组合时,应用不等式组求解
例2:当x=-4时,求二次根式 的值.
解:将x=-4代入二次根式,得
例题讲解
若二次根式 的值为3,求 x 的值.
解:由题意得:
两边同时平方得:
例3:已知 +|3b-9|+(4-c)2=0,求 2a-b+c 的值.
解: ∵ ≥0,|3b-9|≥0,(4-c) 2≥0,
又∵ +|3b-9|+(4-c) 2=0 ,
∴a+2=0 , 3b-9=0 , 4-c=0.
∴a= -2 , b= 3 ,c= 4
∴2a-b+c=2×(-2) -3+4 = -3.
例题讲解
若a,b为实数 ,且
求 的值.
解:
课堂总结
1、二次根式的概念.
2、根号内字母的取值范围.
今天我们学习了哪些知识?
1. 下列各式是二次根式吗
是
不是
不是
是
是
是
不是
不是
不是
不是
课堂练习
2. x取何值时,下列二次根式有意义?
4、若二次根式 的值为3,求x的值
3、当x=-2时,求二次根式 的值
提示:x=3或x=-3
提示:值为1
5. 已知
,求 的值.
解: 由题意得,
6. 一艘轮船先向东北方向航行2小时,再向西北方向航行t小时,船的航速是每时25千米.
(1) 用关于t的代数式表示船离开出发地的距离.
(2) 求当t=3时,船离开出发地多少千米.(精确到0.01)
东
北
解: (1)设船离出发地的距离为s千米
45°
45°
45°
(2)当t=3时
答:当t=3时,船离开出发地90.14千米.
1.作业本1 2.3有理数的乘法(1)
2.自主练习
作业布置
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
