4.1.3比例线段

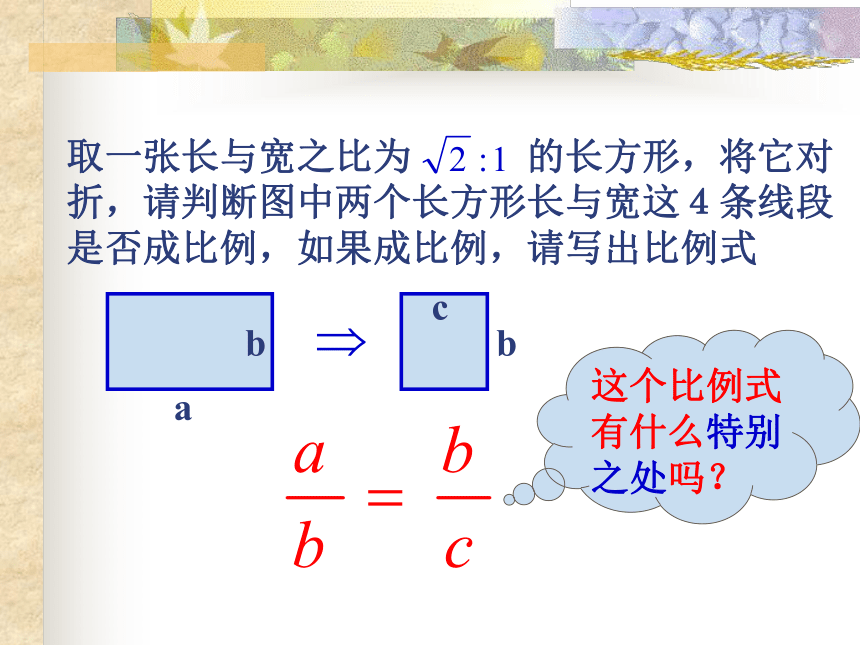
课件20张PPT。4.1.3 比例线段感受匀称、协调之美请你欣赏新西兰朝 鲜新加坡中华人民共和国 上述的国旗中有共同图案吗？取一张长与宽之比为　　　的长方形，将它对折，请判断图中两个长方形长与宽这４条线段是否成比例，如果成比例，请写出比例式这个比例式有什么特别之处吗？一般地，如果三个数a,b,c满足比例式　　　　　　　　
则b就叫a,c的比例中项(2) 和 的比例中项是什么？注意：线段的比例中项是一个正数，而数的比例中项是一对相反数是±14cm著名画家达?芬奇的名画＜蒙娜丽莎＞，画中脸部被围在矩形ＡＢＣＤ中，图中四边形ＢＣＥＦ为正方形，而在线段上的点Ｆ把线段分成两条线段，其中ＤＣＥEF思考:如何求出黄金比的数值?概念：1.已知点C是线段AB的黄金分割点，且AC>CB
则下列等式成立的是（ ）
(A) AB=AC?CB (B) CB=AC?AB
(C) AC=CB?AB (D) AC2=AB?BC
2.已知：线段AB=18cm ，点C是AB的黄金分割点，且AC>BC ，求AC和BC的长.
牛刀小试：若矩形的宽与长的比约为0.618,这样的矩形称之为黄金矩形.自己动手找黄金分割点观察与欣赏 她的上半
身和下半身的比值接近
0.618. 世界艺术珍品——维纳斯女神观察 欣赏 ，她是西元前一
百多年希腊雕塑鼎盛时
期的代表作，你知道芭蕾舞演员跳舞时为什么要掂起脚尖吗?芭蕾舞演员的身段是苗条的，但下半身与身高的比值也只有0.58左右，演员在表演时掂起脚尖，身高就可以增加6-8cm.这时比值就接近0.618了,给人以更为优美的艺术形象.芭蕾舞（1）过已知线段AB的端点B作BC⊥AB
使
例５：已知线段AB=a，用直尺和圆规作出它的黄金分割点。aAB作法:（2）连接AC，在CA上截取CD=CB（3）在AB上截取AP=AD
所以，点P就是线段a的黄金分割点。4.上海东方明珠电视塔高468m,上球体是塔身的黄金分割点,它到塔底部的距离大约是多少米(精确到0.1m)?468m?468×0.618≈289.2m学 而 不 思 则 罔回头一看，我想说…课堂小结：1.比例中项的概念；
2.线段的比例中项与数的比例中项的区别；
3.黄金分割，黄金分割点，黄金比的概念；
4.通过计算来作图，体现数形结合思想
5.黄金分割在生活中的应用。追溯黄金分割的历史文化 早在古希腊，数学家、天文学家欧多克索斯（Eudoxus，约前400——前347）曾提出：能否将一条线段分成不相等的两部分，使较短线段与较长线段的比等于较长线段与原线段的比？这就是黄金分割问题.
而发现黄金分割的是古希腊哲学家毕达哥拉斯。一天，毕达哥拉斯从一家铁匠铺路过，被铺子中那有节奏的叮叮当当的打铁声所吸引，便站在那里仔细聆听，似乎这声音中隐匿着什么秘密。他走进作坊，拿出一把尺量了一下铁锤和铁砧的尺寸，发现它们之间存在着一种十分和谐的关系。回到家里，毕达哥拉斯拿出一根线，想将它分为两段。怎样分才最好呢？经过反复比较，他最后确定0.618 ：1的比例截断最优美。后来，意大利著名科学家、艺术家达·芬奇给这个比例冠以“黄金”二字的美名。