1.3 第3课时 二次根式的实际应用 同步练习(含答案)
文档属性
| 名称 | 1.3 第3课时 二次根式的实际应用 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-22 08:42:38 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第3课时 二次根式的实际应用
知识点1 坡比问题
1.如图1-3-4,已知斜坡AB,且BC⊥AC,则斜坡AB的坡比指的是 ( )
图1-3-4
A.AB∶BC B.AB∶AC
C.AC∶BC D.BC∶AC
2.已知一斜坡的坡比为1∶,坡长为26米,那么坡高为 ( )
A.13 米 B.13 米
C.26 米 D. 米
3.在坡比为1∶2的山坡上种树,要求株距(相邻两树之间的水平距离)为6米,则斜坡上相邻两树间的坡面距离是 米.
4.(教材例6变式)如图1-3-5,一段河坝的横截面为梯形ABCD,试根据图中数据,求出坝底宽AD(i=CE∶ED,单位:m).
图1-3-5
知识点2 几何图形问题
5.长方形相邻两边长分别为,,则它的周长和面积分别是 ( )
A.,4 B.2,4
C.4,3 D.6,4
6.若一个三角形的一条边的长为+1,其面积为6,则这条边上的高线长为 ( )
A.3 B.6-6 C.3+3 D.6+6
7.古希腊的几何学家海伦和我国南宋时期数学家秦九韶都曾提出利用三角形的三边求面积公式,称为海伦——秦九韶公式,如果一个三角形的三边长分别是a,b,c,记p=,那么三角形的面积为S=.在△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,若a=3,b=4,c=5,则△ABC的面积为 ( )
A.5 B.25 C.6 D.36
8.边长是8的等边三角形的高线长是 .
9.(教材作业题T1变式)在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b,若a∶c=1∶3,则= .
10.在数学课上,老师将一长方形纸片的长增加2 cm,宽增加7 cm,就得到了一个面积为192 cm2的正方形纸片,求原长方形纸片的面积.
11.已知直角三角形的两条边长分别是和,则第三条边长是 ( )
A. B.3 C.或3 D.或2
12.如图1-3-6,港口A在观测站O的正东方向,OA=4 km,某船从港口A出发,沿北偏东15°方向航行一段路程后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的路程(即AB的长)为( )
图1-3-6
A.2 km B.2 km C.4 km D.(+1)km
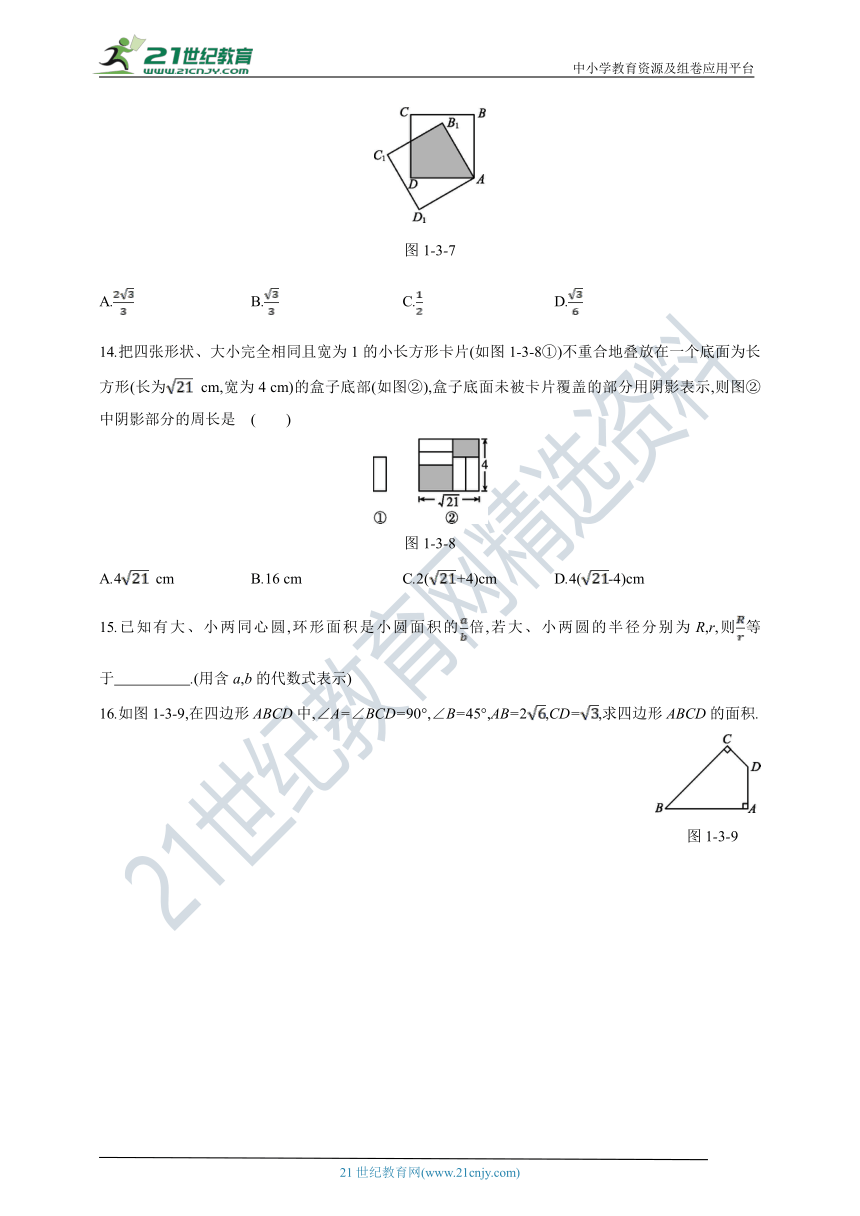
13.把边长均为1的正方形ABCD与正方形AB1C1D1按如图1-3-7所示的方式摆放,且∠BAB1=30°,则图中阴影部分的面积为 ( )
图1-3-7
A. B. C. D.
14.把四张形状、大小完全相同且宽为1的小长方形卡片(如图1-3-8①)不重合地叠放在一个底面为长方形(长为 cm,宽为4 cm)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中阴影部分的周长是 ( )
图1-3-8
A.4 cm B.16 cm C.2(+4)cm D.4(-4)cm
15.已知有大、小两同心圆,环形面积是小圆面积的倍,若大、小两圆的半径分别为R,r,则等于 .(用含a,b的代数式表示)
16.如图1-3-9,在四边形ABCD中,∠A=∠BCD=90°,∠B=45°,AB=2,CD=,求四边形ABCD的面积.
图1-3-9
17.已知:如图1-3-10,P为线段AB上的动点(与A,B两点不重合).在同一平面内,把线段AP,BP分别折成△CDP,△EFP,其中∠CDP=∠EFP=90°,且D,P,F三点共线.若△CDP,△EFP均为等腰三角形,且DF=2,求AB的长.
图1-3-10
详解详析
1.D 2.B 3.3
4.解:过点B作BF⊥AD于点F,则BF=CE=4 m,EF=BC=4.5 m.
在Rt△ABF中,AF===3(m).
在Rt△CED中,根据i=,
可知ED===4(m),
则AD=AF+EF+ED=3+4.5+4=(7.5+4)m.
答:坝底宽AD为(7.5+4)m.
5.D [解析] 由题意,得长方形的周长=2(+)=2(+2)=2×3=6,长方形的面积=×=×2=4.故选D.
6.B
7.C [解析] ∵P===6,
∴S=
=
=
=6.
故选C.
8.4 9.
10.解:∵一个面积为192 cm2的正方形纸片的边长为8 cm,
∴原长方形纸片的长为8-2=6(cm),宽为8-7=(cm),
则原长方形纸片的面积为6×=18(cm2).
11.C [解析] 若和都是直角边长,根据勾股定理得斜边长为3;若和是一条直角边长和一条斜边长,根据勾股定理得另一条直角边长为.
12.A [解析] 如图,过点A作AD⊥OB于点D.
在Rt△AOD中,∵∠ADO=90°,∠AOD=30°,OA=4 km,
∴AD=OA=2(km).
在Rt△ABD中,∵∠ADB=90°,∠B=∠CAB-∠AOB=75°-30°=45°,
∴BD=AD=2 km,
∴AB==2(km).
则该船航行的路程(即AB的长)为2 km.
故选A.
13.B
14.B
15. [解析] ∵环形面积是小圆面积的倍,
∴大圆面积是小圆面积的倍,
则=,
∴=.
16.解:如图,延长BC,AD相交于点E.
∵∠A=90°,∠B=45°,
∴△ABE是等腰直角三角形,
∴S△ABE=AB2=12.
同理,△CDE也是等腰直角三角形,
∴S△CDE=CD2=,
∴S四边形ABCD=S△ABE-S△CDE=.
17.解:设DP=x,则PF=2-x.
∵∠CDP=∠EFP=90°,且△CDP,△EFP均为等腰三角形,
∴CD=x,CP=x,EF=2-x,PE=(2-x),
∴AB=x+x+x+2-x+2-x+(2-x)=4+2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第3课时 二次根式的实际应用
知识点1 坡比问题
1.如图1-3-4,已知斜坡AB,且BC⊥AC,则斜坡AB的坡比指的是 ( )
图1-3-4
A.AB∶BC B.AB∶AC
C.AC∶BC D.BC∶AC
2.已知一斜坡的坡比为1∶,坡长为26米,那么坡高为 ( )
A.13 米 B.13 米
C.26 米 D. 米
3.在坡比为1∶2的山坡上种树,要求株距(相邻两树之间的水平距离)为6米,则斜坡上相邻两树间的坡面距离是 米.
4.(教材例6变式)如图1-3-5,一段河坝的横截面为梯形ABCD,试根据图中数据,求出坝底宽AD(i=CE∶ED,单位:m).
图1-3-5
知识点2 几何图形问题
5.长方形相邻两边长分别为,,则它的周长和面积分别是 ( )
A.,4 B.2,4
C.4,3 D.6,4
6.若一个三角形的一条边的长为+1,其面积为6,则这条边上的高线长为 ( )
A.3 B.6-6 C.3+3 D.6+6
7.古希腊的几何学家海伦和我国南宋时期数学家秦九韶都曾提出利用三角形的三边求面积公式,称为海伦——秦九韶公式,如果一个三角形的三边长分别是a,b,c,记p=,那么三角形的面积为S=.在△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,若a=3,b=4,c=5,则△ABC的面积为 ( )
A.5 B.25 C.6 D.36
8.边长是8的等边三角形的高线长是 .
9.(教材作业题T1变式)在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b,若a∶c=1∶3,则= .
10.在数学课上,老师将一长方形纸片的长增加2 cm,宽增加7 cm,就得到了一个面积为192 cm2的正方形纸片,求原长方形纸片的面积.
11.已知直角三角形的两条边长分别是和,则第三条边长是 ( )
A. B.3 C.或3 D.或2
12.如图1-3-6,港口A在观测站O的正东方向,OA=4 km,某船从港口A出发,沿北偏东15°方向航行一段路程后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的路程(即AB的长)为( )
图1-3-6
A.2 km B.2 km C.4 km D.(+1)km
13.把边长均为1的正方形ABCD与正方形AB1C1D1按如图1-3-7所示的方式摆放,且∠BAB1=30°,则图中阴影部分的面积为 ( )
图1-3-7
A. B. C. D.
14.把四张形状、大小完全相同且宽为1的小长方形卡片(如图1-3-8①)不重合地叠放在一个底面为长方形(长为 cm,宽为4 cm)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中阴影部分的周长是 ( )
图1-3-8
A.4 cm B.16 cm C.2(+4)cm D.4(-4)cm
15.已知有大、小两同心圆,环形面积是小圆面积的倍,若大、小两圆的半径分别为R,r,则等于 .(用含a,b的代数式表示)
16.如图1-3-9,在四边形ABCD中,∠A=∠BCD=90°,∠B=45°,AB=2,CD=,求四边形ABCD的面积.
图1-3-9
17.已知:如图1-3-10,P为线段AB上的动点(与A,B两点不重合).在同一平面内,把线段AP,BP分别折成△CDP,△EFP,其中∠CDP=∠EFP=90°,且D,P,F三点共线.若△CDP,△EFP均为等腰三角形,且DF=2,求AB的长.
图1-3-10
详解详析
1.D 2.B 3.3
4.解:过点B作BF⊥AD于点F,则BF=CE=4 m,EF=BC=4.5 m.
在Rt△ABF中,AF===3(m).
在Rt△CED中,根据i=,
可知ED===4(m),
则AD=AF+EF+ED=3+4.5+4=(7.5+4)m.
答:坝底宽AD为(7.5+4)m.
5.D [解析] 由题意,得长方形的周长=2(+)=2(+2)=2×3=6,长方形的面积=×=×2=4.故选D.
6.B
7.C [解析] ∵P===6,
∴S=
=
=
=6.
故选C.
8.4 9.
10.解:∵一个面积为192 cm2的正方形纸片的边长为8 cm,
∴原长方形纸片的长为8-2=6(cm),宽为8-7=(cm),
则原长方形纸片的面积为6×=18(cm2).
11.C [解析] 若和都是直角边长,根据勾股定理得斜边长为3;若和是一条直角边长和一条斜边长,根据勾股定理得另一条直角边长为.
12.A [解析] 如图,过点A作AD⊥OB于点D.
在Rt△AOD中,∵∠ADO=90°,∠AOD=30°,OA=4 km,
∴AD=OA=2(km).
在Rt△ABD中,∵∠ADB=90°,∠B=∠CAB-∠AOB=75°-30°=45°,
∴BD=AD=2 km,
∴AB==2(km).
则该船航行的路程(即AB的长)为2 km.
故选A.
13.B
14.B
15. [解析] ∵环形面积是小圆面积的倍,
∴大圆面积是小圆面积的倍,
则=,
∴=.
16.解:如图,延长BC,AD相交于点E.
∵∠A=90°,∠B=45°,
∴△ABE是等腰直角三角形,
∴S△ABE=AB2=12.
同理,△CDE也是等腰直角三角形,
∴S△CDE=CD2=,
∴S四边形ABCD=S△ABE-S△CDE=.
17.解:设DP=x,则PF=2-x.
∵∠CDP=∠EFP=90°,且△CDP,△EFP均为等腰三角形,
∴CD=x,CP=x,EF=2-x,PE=(2-x),
∴AB=x+x+x+2-x+2-x+(2-x)=4+2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
