第3章直线与圆、圆与圆的位置关系导学案
图片预览


文档简介
第3章直线与圆、圆与圆的位置关系
3.1 直线与圆的位置关系(1)
我预学
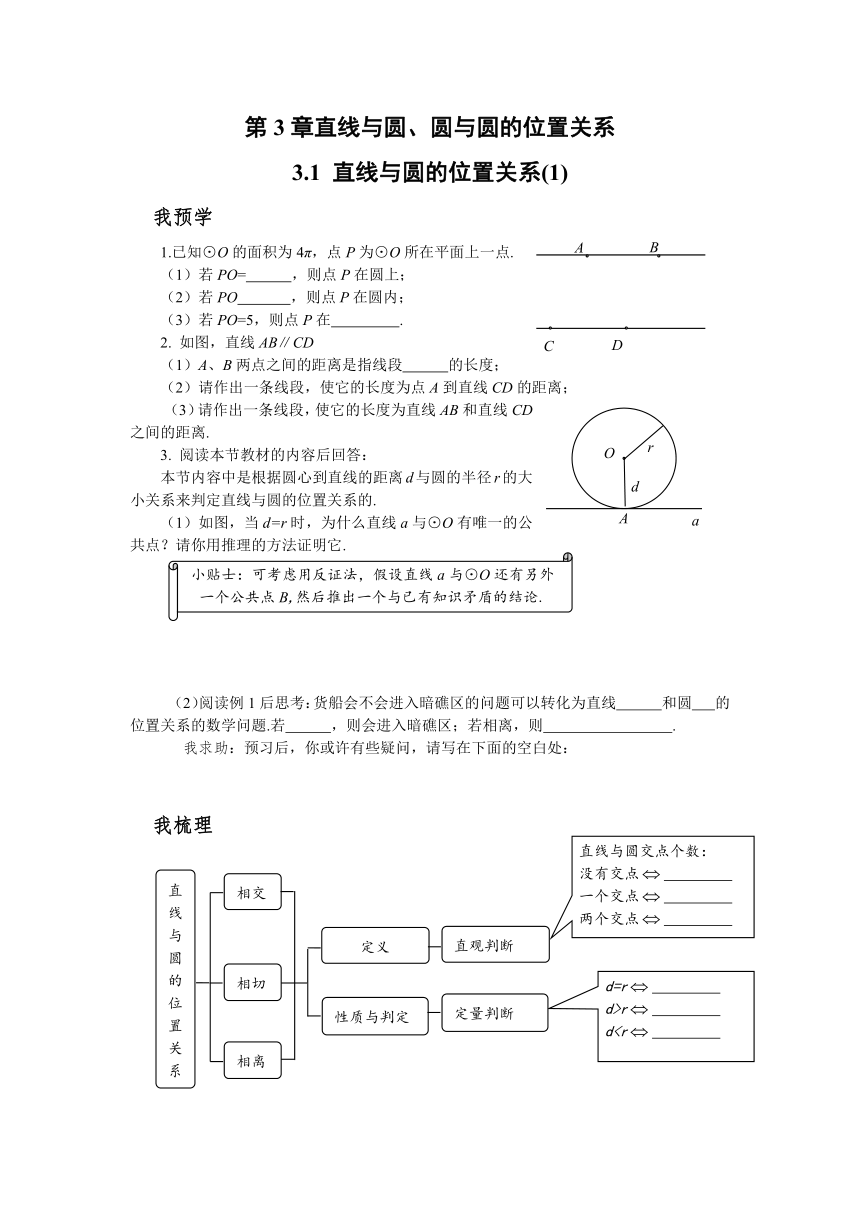
1.已知⊙O的面积为4π,点P为⊙O所在平面上一点.
(1)若PO= ,则点P在圆上;
(2)若PO ,则点P在圆内;
(3)若PO=5,则点P在 .
2. 如图,直线AB∥CD
(1)A、B两点之间的距离是指线段 的长度;
(2)请作出一条线段,使它的长度为点A到直线CD的距离;
(3)请作出一条线段,使它的长度为直线AB和直线CD之间的距离.
3. 阅读本节教材的内容后回答:
本节内容中是根据圆心到直线的距离d与圆的半径r的大小关系来判定直线与圆的位置关系的.
(1)如图,当d=r时,为什么直线a与⊙O有唯一的公共点?请你用推理的方法证明它.
(2)阅读例1后思考:货船会不会进入暗礁区的问题可以转化为直线 和圆 的位置关系的数学问题.若 ,则会进入暗礁区;若相离,则 .
我求助:预习后,你或许有些疑问,请写在下面的空白处:
我梳理
我反思:通过本节课的学习,你一定有很多感想和收获,请写在下面的空白处:
我达标
1.已知⊙O的半径r=2cm,直线l与圆心的距离d=cm,则直线l与⊙O的位置关系是 ( )
A.相交 B.相切 C.相离 D.直线l在⊙O外
2.已知⊙O的直径等于8cm,直线l与⊙O只有一个公共点,那么圆心O到直线l的距离是 cm..
3.已知⊙O的直径为12cm,如果圆心O到直线m的距离为5cm,那么直线m与⊙O的公共点的个数为 个.
4.正方形ABCD的边长为,以A为圆心,2为半径作⊙A,则与对角线BD所在直线的位置关系是 .
5.如图,已知△ABC,求作以A为圆心,且与BC
边相切的圆.(保留痕迹,不写画法)
6.如图,点A是一个半径为300m的圆形森林公园的中心,在它的附近有B、C两个村庄,现在要在B、C两个村庄之间修一条长为1000m的笔直的公路将两个村庄联通,已测得∠ABC=45°,∠ACB=30°.这条公路是否会穿过该深林公园?请通过计算进行说明。
7.如图,直角梯形ABCD中,∠A=∠B=90°,AD∥BC,E为AB上一点,且DE平分∠ADC, CE平分∠DCB,以AB为直径的圆与直线CD有怎样的位置关系?请说明理由.
我挑战
8.已知已知⊙O的半径3cm,直线l上有一点P,线段PO的长度为3cm,则直线l与圆的位置关系是( )
A.相交 B.相切 C.相离 D.相交或相切
9.在Rt△ABC中,∠A=90°,AC=3,BC=5,⊙A的半径为r,若线段BC与⊙A无公共点,则r应满足的条件是 ;若射线BC与⊙A有两个公共点,则r应满足的条件是 .
10.在射线OA上取一点A,使OA=4cm,以A为圆心,作一个直径为4cm的圆.过点O的射线OB与OA所夹的锐角α取怎样的值时,⊙A与直线OB(1)相离;(2)相切;(3)相交.
我登峰
11.如图,点P为正比例函数的图像上一个动点,⊙P的半径为3,设点P的坐标为(x,y).
(1)求当⊙P与直线x=2相切时,点P的坐标;
(2)请直接写出⊙P与直线x=2相交和相离时x的取值范围.
3.1 直线与圆的位置关系(2)
我预学
直线和圆相切的判定方法:
(1)若直线和圆有 公共点,则直线和圆相切;
(2)若圆心到直线的距离 ,则直线和圆相切.
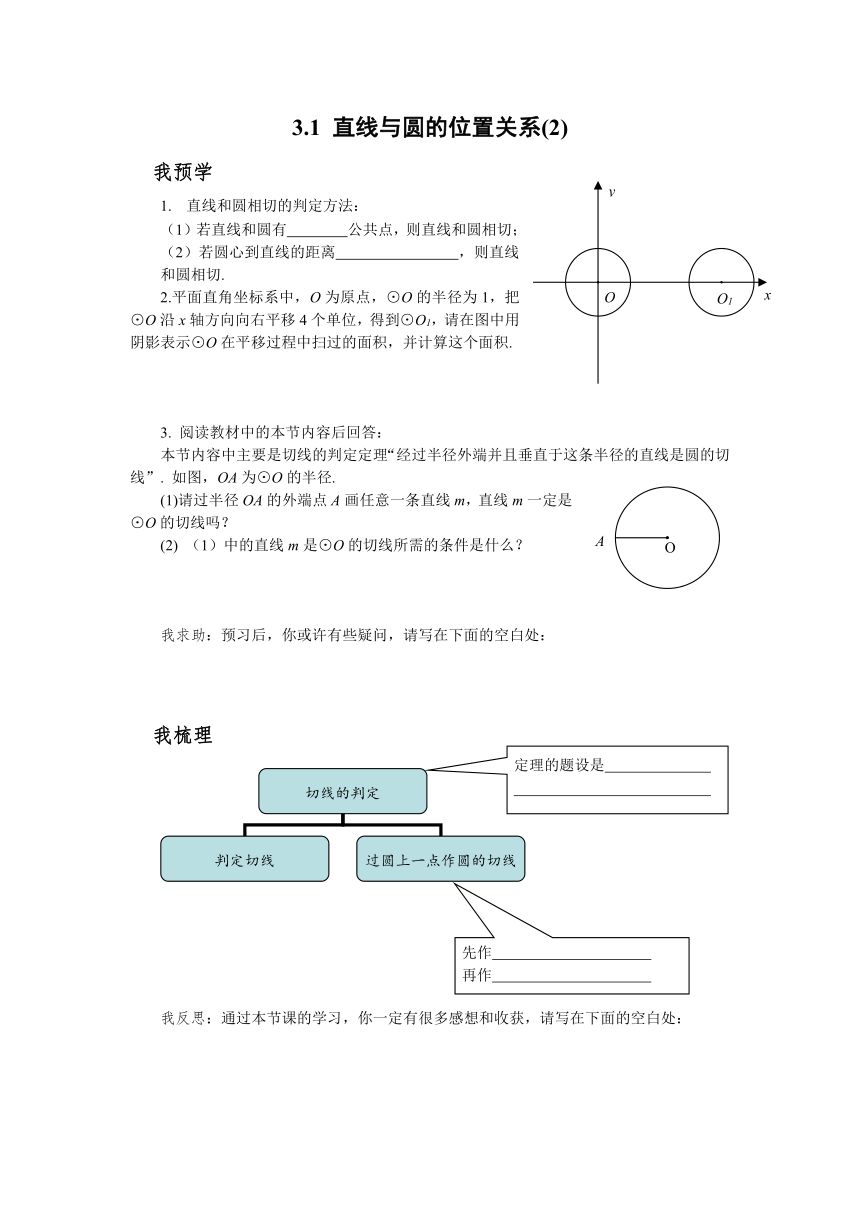
2.平面直角坐标系中,O为原点,⊙O的半径为1,把⊙O沿x轴方向向右平移4个单位,得到⊙O1,请在图中用阴影表示⊙O在平移过程中扫过的面积,并计算这个面积.
3. 阅读教材中的本节内容后回答:
本节内容中主要是切线的判定定理“经过半径外端并且垂直于这条半径的直线是圆的切线”. 如图,OA为⊙O的半径.
(1)请过半径OA的外端点A画任意一条直线m,直线m一定是⊙O的切线吗?
(2) (1)中的直线m是⊙O的切线所需的条件是什么?
我求助:预习后,你或许有些疑问,请写在下面的空白处:
我梳理
我反思:通过本节课的学习,你一定有很多感想和收获,请写在下面的空白处:
我达标
1.下列说法中正确的是( )
A.垂直于直径的直线是圆的切线
B.经过半径外端的直线是圆的切线
C.若圆心到直线上一点的距离等于半径,则该直线是圆的切线
D.经过半径外端且垂直于这条半径的直线是圆的切线
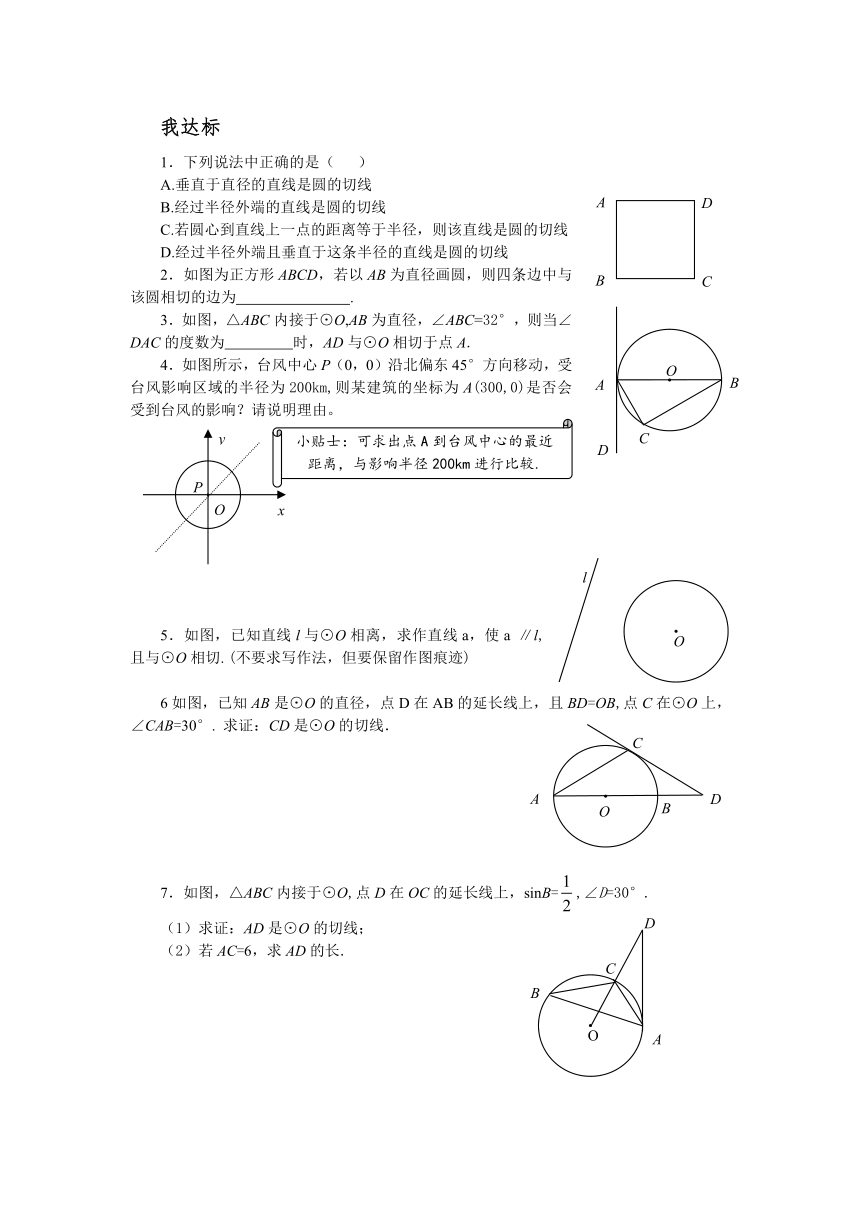
2.如图为正方形ABCD,若以AB为直径画圆,则四条边中与该圆相切的边为 .
3.如图,△ABC内接于⊙O,AB为直径,∠ABC=32°,则当∠DAC的度数为 时,AD与⊙O相切于点A.
4.如图所示,台风中心P(0,0)沿北偏东45°方向移动,受台风影响区域的半径为200km,则某建筑的坐标为A(300,0)是否会受到台风的影响?请说明理由。
5.如图,已知直线l与⊙O相离,求作直线a,使a ∥l,且与⊙O相切. (不要求写作法,但要保留作图痕迹)
6如图,已知AB是⊙O的直径,点D在AB的延长线上,且BD=OB,点C在⊙O上,∠CAB=30°. 求证:CD是⊙O的切线.
7.如图,△ABC内接于⊙O,点D在OC的延长线上,sinB=,∠D=30°.
(1)求证:AD是⊙O的切线;
(2)若AC=6,求AD的长.
我挑战
8.在平面直角坐标系中,点A(3,3),以A为圆心,为半径作圆,则⊙A与直线y= -x的位置关系是 .
9.如图,∠ABC=90°,O为射线BC上一点,以点O为圆心,为半径作⊙O,要使AB与⊙O相切,需要把射线AB绕点B顺时针旋转的度数为 .
10.要用尺规过⊙O外一点P作⊙O的切线,如图,可以先连结PO,再作PO的中点Q,然后以Q为圆心,PQ为半径作⊙Q交⊙O于点A,连结PA,则PA就是⊙O的切线,A为切点.请你证明这种作法是正确的.
我登峰
11.如图,⊙D的圆心坐标为(0,1),⊙D交y轴于点A、B,交x轴于点C,过点C的直线:y=x-8与y轴交于点P.
(1)试判断PC与⊙D的位置关系;
(2)判断直线PC上是否存在点E,使得S△EOP =4S△CDO,若存在,求出点E的坐标;若不存在,请说明理由.
3.1 直线与圆的位置关系(3)
我预学
1.关于切线的性质我们已经学过两个.如图,直线m与⊙O相切于点A,请回答谢列问题:.
(1)直线m与⊙O除点A外,还有其它的公共点吗?答:
(2)若⊙O的半径为3cm,则点O到直线m的距离为 cm.
2.阅读教材中的本节内容后回答:
(1)请把教材中圆的切线的两个性质分别改写为“如果……那么……”的表述形式:
① ;
② .
(2)教材中圆的切线的两个性质的题设和结论中有共性的地方,请你结合第1题的图,用几何语言(或者用自己的话)表述两个定理.
3.预学教材中的例题5后尝试解决如下问题:
如图,已知Rt△ABC中,∠ACB=Rt∠,D为斜边AB上一点,且BD=BC,求证:∠ACD=∠DBC.(可挑战两种证法)
我求助:预习后,你或许有些疑问,请写在下面的空白处:
我梳理
对于切线的性质,可以分解为:(1)直线与圆的切线垂直;(2)直线经过切点;(3)直线经过圆心.这三句话中任意两个作题设就可以推出第三个,请完成下表:
题设
直线m过圆心O
直线m过切点A
直线m⊥切线l
直线m过圆心O
结论
直线m过圆心O
我反思:通过本节课的学习,你一定有很多感想和收获,请写在下面的空白处:
我达标
1.已知半径为3cm的⊙O外一点P,PO=5cm,PQ切⊙O于点Q,则PQ= cm.
2.如图所示,线段AB经过经过圆心O,交⊙O于点A、C,∠B=30°,直线BD与⊙O相切于点D,则∠ADB的度数为 .
3.如图,AP与⊙O相切于点P,OA交⊙O于点B,∠A=40°,则∠APB= 度.
4.在平面直角坐标系中,⊙P的圆心坐标为(a,0),直径为6.若⊙P与y轴相切,则a的值为 .
5.如图,OA⊥OB,点C在OB延长线上,且CB=BO,CD切⊙O于点D,连结AD,求∠OAD的度数.
6.如图,已知AP是⊙O的切线,A为切点,点B在⊙O上,且PA=PB.求证:PB是⊙O的切线.
7.如图,已知等腰△ABC中,AB=AC=10cm,BC=12cm,点O在BC上,以O点为圆心作圆,和两腰都相切,求⊙O的半径.
我挑战
8.如图,PA、PB切⊙O于点A、B.
(1)若点C是⊙O上一点,且∠ACB=70°,则∠P的度数为 .
(2)若∠P=40°,点C为⊙O上一个动点(不与A、B重合),则∠ACB等于 度.
9.如图,AB是⊙O的切线,A为切点,AC是⊙O的弦,过点O作OH⊥AC于点H.若OH=2,AB=12,BO=13.求弦AC的长.
10.如图,在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,⊙O的半径为1cm,CB=3cm.求AD的长.
我登峰
11.如图,⊙O的直径AB=6cm,P是AB延长线上的一点,过点P作⊙O的切线,切点为C,连结AC.
(1)若∠CPA=30°,求PC的长;
(2)若点P在AB的延长线运动,∠CPA的平分线交AC于点M,∠CMP的大小会发生变化吗?若变化,请说明理由;若不变,请求出∠CMP的值。
3.2 三角形的内切圆
我预学
1. 如图,已知∠ABC.
(1)请用尺规作出∠ABC的角平分线;若点P为这条角平分线上的任意一点,则点P到AB、BC的距离有怎样的数量关系?
(2)在角的内部,满足到角两边BA、BC的距离相等的点在怎样的一条线上?
2. 如图,已知点△ABC .
(1)若求作一点P,使点P到线段AB、BC的距离相等,这样的点P你能作 个;
(2)求作一点P,使点P到△ABC三边的距离相等,这样的点P你能作 个,请你在图中用直尺和圆规作出点P.
3. 阅读教材中的本节内容后解答:
(1)本节内容有两个重要概念:三角形的内切圆和三角形的内心,请类比学习过的三角形的外接圆、三角形的外心,“内”与“外”是相对于什么定义的?你是怎么理解的?
(2)请比较三角形的外接圆和内切圆的作法,分别是怎么确定圆心和半径的,结合第2题中的图形加以说明.
(3)请猜想例2中线段AE和AF,CE和CD,BF和BD分别有怎样的数量关系?并证明你的猜想(结合第2题图).请你由此概括得出一个命题.
我求助:预习后,你或许有些疑问,请写在下面的空白处:
我梳理
我反思:通过本节课的学习,你一定有很多感想和收获,请写在下面的空白处:
我达标
1.若点P为△ABC内心,则( )
A.点P为三边中线的交点 B.点P为三边中垂线的交点
C.点P到三顶点的距离相等 D.点P到三边的距离相等
2.在△ABC中,I为内心,若∠A =70°,则∠BIC= ,若O为外心,则∠BOC= .
3.等边三角形的内切圆半径与外接圆半径之比为 .
4.如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9cm,BC=14cm,CA=13cm.则AF= ,BD= ,CE= .
5.如图,有一块三边分别为0.4m,0.5m和0.6m的三角形铝皮,怎样才能剪出一个面积最大的圆形铝皮?请你设计出裁剪方案,并在图中画出来(不要求写作法,但要保留作图痕迹).
6.如图,⊙O内切于△ABC,与AB,BC,CA分别相切于点D,E,F,∠DEF=50°,求∠A的度数.
7.已知:如图,在△ABC中,⊙O截△ABC的三边所得的弦长相等,求证:O是△ABC的内心.
我挑战
8.若三角形的三边之比为3∶4∶5,则它的内切圆与外接圆的半径之比为 .
9.如图,DE是△ABC的内切圆⊙O的切线,D,E分别在AB,AC上,已知BC=2,△ADE的周长是4,则△ABC的周长为 .
10.如图,⊙O是△ABC的内切圆,切点分别是D,E,F,AB=AC=10,BC=12,求:
(1)AD的长;
(2)△ABC的面积;
(3)⊙O的半径.
我登峰
11.如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,其内切圆⊙I分别切BC,AC,AB于点D,E,F.
(1)试说明:⊙I的半径r=(a+b-c);
(2)若BD和AE是方程x2-5x+6=0的两个根(BD(3)在(2)的条件下,求△ABC的内切圆与外接圆的圆心距.
3.3圆与园的位置关系
我预学
1.如图,已知∠ABC=30°,点M在BC上,且BM=5cm,当r分别取下列值时,以M为圆心,r为半径的圆与直线BA分别有怎样的位置关系?
(1)r=2cm;
(2)r=4cm;
(3)r=2.5cm.
2.阅读教材中的本节内容后回答:
记两个圆的圆心距为d,两个圆的半径为R、r.
(1)在d、R、r、R+r、R-r五个量中,判断两个圆的位置关系时只需要关注哪三个量?
(2)当d< R+r时,两圆有怎样的位置关系?
(3)阅读教材的例题后你发现解决两圆相切问题最常用的辅助线是什么?
我求助:预习后,你或许有些疑问,请写在下面的空白处:
我反思:通过本节课的学习,你一定有很多感想和收获,请写在下面的空白处:
我达标
1.已知两圆的半径分别是2和4,圆心距是3,则这两圆的位置关系是( )
A.内含 B.内切 C.相交 D.外切
2.已知⊙O1的半径为3cm ,⊙O2 的半径为4cm,若⊙O1和⊙O2 相切,则这两个圆的圆心距为 ;若⊙O1和⊙O2 无公共点,则两圆的圆心距d的取值范围是 .
3.两个圆的圆心都是点O,半径分别是3cm和6cm,若⊙P与小圆外切,同时与大圆内切,则⊙P的半径为 ,若⊙M与小圆内切,同时与大圆也内切,则⊙M的半径为 .
4.若⊙O1的圆心坐标为(2,0),半径为1,⊙O2的.圆心坐标为(-1,0),半径为3,则这两圆的位置关系为 .
5.如图,⊙O的半径为4cm,点P是⊙O外一点,OP=6cm。作图并解答:
(1)以点P为圆心作⊙P与⊙O外切,则⊙P的半径是多少?
(2)以点P为圆心作⊙P与⊙O内切,则⊙P的半径是多少?
6.如图,⊙O1和⊙O2外切于点P,过点P的直线分别交⊙O1,⊙O2与A,B,已知⊙O1与⊙O 2的面积比为3∶2,求AP∶BP.
7.某市公园的一个雕塑,它是由三个直径为1m的圆两两相磊立在水平的地面上(如图),则雕塑的最高点到地面的距离是多少?
我挑战
8. 工人师傅在一个长为25cm,宽为18cm的矩形铁皮上,剪去一个和三边都相切的圆后,在剩余部分的铁皮上再剪出一个最大的圆,则这个最大圆的半径为 .
9.如图,半圆O的直径AB=4,与半圆O内切的动圆O1与AB相切于点M,设⊙O1的半径为y,AM长为x,则y关于x的函数关系式是 .
10.已知⊙O1和⊙O2的半径分别为1和3,且⊙O1和⊙O2外切,则在平面上,半径为4且与⊙O1和⊙O2都相切的圆有几个?请你画一画.若半径为5,且与⊙O1和⊙O2都相切的圆又可以画几个?
我登峰
11.已知Rt△ABC中,∠ABC=90°,AC=6,BC=8.
(1)如图,若半径为r1的⊙O1是Rt△ABC内切圆,求r1的值;
(2)如图,若半径为r2的两个等圆⊙O1和⊙O2外切,且⊙O1与AC,BA相切,⊙O2与BC,BA相切,求r2的值.
(3)请你类比问题(1)(2),拓展到Rt△ABC的内部有n个圆外切的情况,提出一个类似的问题,并解决你提出的问题.
3.1 直线与圆的位置关系(3)
1. 4 2. 120°3. 25° 4. ± 3 5.75° 6.略 7.4.8 8.(1)40° (2)70°或110° 9. 2 10. 11.(1)3 (2)45°
3.2 三角形的内切圆
1.D 2.125°140° 3.1∶2 4.AF=4cm,BD=5cm,CE=9cm 5.作△ABC的内切圆 6.80°7.略 8.2∶5 9.8 10.(1)4 (2)48 (3)3 11.(1)略 (2)BA=5,AC=4,BC=3 (3)
3.3圆与园的位置关系
1. C 2. 1cm或7cm d>7或0cm
3.1 直线与圆的位置关系(1)
我预学
1.已知⊙O的面积为4π,点P为⊙O所在平面上一点.
(1)若PO= ,则点P在圆上;
(2)若PO ,则点P在圆内;
(3)若PO=5,则点P在 .
2. 如图,直线AB∥CD
(1)A、B两点之间的距离是指线段 的长度;
(2)请作出一条线段,使它的长度为点A到直线CD的距离;
(3)请作出一条线段,使它的长度为直线AB和直线CD之间的距离.
3. 阅读本节教材的内容后回答:
本节内容中是根据圆心到直线的距离d与圆的半径r的大小关系来判定直线与圆的位置关系的.
(1)如图,当d=r时,为什么直线a与⊙O有唯一的公共点?请你用推理的方法证明它.
(2)阅读例1后思考:货船会不会进入暗礁区的问题可以转化为直线 和圆 的位置关系的数学问题.若 ,则会进入暗礁区;若相离,则 .
我求助:预习后,你或许有些疑问,请写在下面的空白处:
我梳理
我反思:通过本节课的学习,你一定有很多感想和收获,请写在下面的空白处:
我达标
1.已知⊙O的半径r=2cm,直线l与圆心的距离d=cm,则直线l与⊙O的位置关系是 ( )
A.相交 B.相切 C.相离 D.直线l在⊙O外
2.已知⊙O的直径等于8cm,直线l与⊙O只有一个公共点,那么圆心O到直线l的距离是 cm..
3.已知⊙O的直径为12cm,如果圆心O到直线m的距离为5cm,那么直线m与⊙O的公共点的个数为 个.
4.正方形ABCD的边长为,以A为圆心,2为半径作⊙A,则与对角线BD所在直线的位置关系是 .
5.如图,已知△ABC,求作以A为圆心,且与BC
边相切的圆.(保留痕迹,不写画法)
6.如图,点A是一个半径为300m的圆形森林公园的中心,在它的附近有B、C两个村庄,现在要在B、C两个村庄之间修一条长为1000m的笔直的公路将两个村庄联通,已测得∠ABC=45°,∠ACB=30°.这条公路是否会穿过该深林公园?请通过计算进行说明。
7.如图,直角梯形ABCD中,∠A=∠B=90°,AD∥BC,E为AB上一点,且DE平分∠ADC, CE平分∠DCB,以AB为直径的圆与直线CD有怎样的位置关系?请说明理由.
我挑战
8.已知已知⊙O的半径3cm,直线l上有一点P,线段PO的长度为3cm,则直线l与圆的位置关系是( )
A.相交 B.相切 C.相离 D.相交或相切
9.在Rt△ABC中,∠A=90°,AC=3,BC=5,⊙A的半径为r,若线段BC与⊙A无公共点,则r应满足的条件是 ;若射线BC与⊙A有两个公共点,则r应满足的条件是 .
10.在射线OA上取一点A,使OA=4cm,以A为圆心,作一个直径为4cm的圆.过点O的射线OB与OA所夹的锐角α取怎样的值时,⊙A与直线OB(1)相离;(2)相切;(3)相交.
我登峰
11.如图,点P为正比例函数的图像上一个动点,⊙P的半径为3,设点P的坐标为(x,y).
(1)求当⊙P与直线x=2相切时,点P的坐标;
(2)请直接写出⊙P与直线x=2相交和相离时x的取值范围.
3.1 直线与圆的位置关系(2)
我预学
直线和圆相切的判定方法:
(1)若直线和圆有 公共点,则直线和圆相切;
(2)若圆心到直线的距离 ,则直线和圆相切.
2.平面直角坐标系中,O为原点,⊙O的半径为1,把⊙O沿x轴方向向右平移4个单位,得到⊙O1,请在图中用阴影表示⊙O在平移过程中扫过的面积,并计算这个面积.
3. 阅读教材中的本节内容后回答:
本节内容中主要是切线的判定定理“经过半径外端并且垂直于这条半径的直线是圆的切线”. 如图,OA为⊙O的半径.
(1)请过半径OA的外端点A画任意一条直线m,直线m一定是⊙O的切线吗?
(2) (1)中的直线m是⊙O的切线所需的条件是什么?
我求助:预习后,你或许有些疑问,请写在下面的空白处:
我梳理
我反思:通过本节课的学习,你一定有很多感想和收获,请写在下面的空白处:
我达标
1.下列说法中正确的是( )
A.垂直于直径的直线是圆的切线
B.经过半径外端的直线是圆的切线
C.若圆心到直线上一点的距离等于半径,则该直线是圆的切线
D.经过半径外端且垂直于这条半径的直线是圆的切线
2.如图为正方形ABCD,若以AB为直径画圆,则四条边中与该圆相切的边为 .
3.如图,△ABC内接于⊙O,AB为直径,∠ABC=32°,则当∠DAC的度数为 时,AD与⊙O相切于点A.
4.如图所示,台风中心P(0,0)沿北偏东45°方向移动,受台风影响区域的半径为200km,则某建筑的坐标为A(300,0)是否会受到台风的影响?请说明理由。
5.如图,已知直线l与⊙O相离,求作直线a,使a ∥l,且与⊙O相切. (不要求写作法,但要保留作图痕迹)
6如图,已知AB是⊙O的直径,点D在AB的延长线上,且BD=OB,点C在⊙O上,∠CAB=30°. 求证:CD是⊙O的切线.
7.如图,△ABC内接于⊙O,点D在OC的延长线上,sinB=,∠D=30°.
(1)求证:AD是⊙O的切线;
(2)若AC=6,求AD的长.
我挑战
8.在平面直角坐标系中,点A(3,3),以A为圆心,为半径作圆,则⊙A与直线y= -x的位置关系是 .
9.如图,∠ABC=90°,O为射线BC上一点,以点O为圆心,为半径作⊙O,要使AB与⊙O相切,需要把射线AB绕点B顺时针旋转的度数为 .
10.要用尺规过⊙O外一点P作⊙O的切线,如图,可以先连结PO,再作PO的中点Q,然后以Q为圆心,PQ为半径作⊙Q交⊙O于点A,连结PA,则PA就是⊙O的切线,A为切点.请你证明这种作法是正确的.
我登峰
11.如图,⊙D的圆心坐标为(0,1),⊙D交y轴于点A、B,交x轴于点C,过点C的直线:y=x-8与y轴交于点P.
(1)试判断PC与⊙D的位置关系;
(2)判断直线PC上是否存在点E,使得S△EOP =4S△CDO,若存在,求出点E的坐标;若不存在,请说明理由.
3.1 直线与圆的位置关系(3)
我预学
1.关于切线的性质我们已经学过两个.如图,直线m与⊙O相切于点A,请回答谢列问题:.
(1)直线m与⊙O除点A外,还有其它的公共点吗?答:
(2)若⊙O的半径为3cm,则点O到直线m的距离为 cm.
2.阅读教材中的本节内容后回答:
(1)请把教材中圆的切线的两个性质分别改写为“如果……那么……”的表述形式:
① ;
② .
(2)教材中圆的切线的两个性质的题设和结论中有共性的地方,请你结合第1题的图,用几何语言(或者用自己的话)表述两个定理.
3.预学教材中的例题5后尝试解决如下问题:
如图,已知Rt△ABC中,∠ACB=Rt∠,D为斜边AB上一点,且BD=BC,求证:∠ACD=∠DBC.(可挑战两种证法)
我求助:预习后,你或许有些疑问,请写在下面的空白处:
我梳理
对于切线的性质,可以分解为:(1)直线与圆的切线垂直;(2)直线经过切点;(3)直线经过圆心.这三句话中任意两个作题设就可以推出第三个,请完成下表:
题设
直线m过圆心O
直线m过切点A
直线m⊥切线l
直线m过圆心O
结论
直线m过圆心O
我反思:通过本节课的学习,你一定有很多感想和收获,请写在下面的空白处:
我达标
1.已知半径为3cm的⊙O外一点P,PO=5cm,PQ切⊙O于点Q,则PQ= cm.
2.如图所示,线段AB经过经过圆心O,交⊙O于点A、C,∠B=30°,直线BD与⊙O相切于点D,则∠ADB的度数为 .
3.如图,AP与⊙O相切于点P,OA交⊙O于点B,∠A=40°,则∠APB= 度.
4.在平面直角坐标系中,⊙P的圆心坐标为(a,0),直径为6.若⊙P与y轴相切,则a的值为 .
5.如图,OA⊥OB,点C在OB延长线上,且CB=BO,CD切⊙O于点D,连结AD,求∠OAD的度数.
6.如图,已知AP是⊙O的切线,A为切点,点B在⊙O上,且PA=PB.求证:PB是⊙O的切线.
7.如图,已知等腰△ABC中,AB=AC=10cm,BC=12cm,点O在BC上,以O点为圆心作圆,和两腰都相切,求⊙O的半径.
我挑战
8.如图,PA、PB切⊙O于点A、B.
(1)若点C是⊙O上一点,且∠ACB=70°,则∠P的度数为 .
(2)若∠P=40°,点C为⊙O上一个动点(不与A、B重合),则∠ACB等于 度.
9.如图,AB是⊙O的切线,A为切点,AC是⊙O的弦,过点O作OH⊥AC于点H.若OH=2,AB=12,BO=13.求弦AC的长.
10.如图,在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,⊙O的半径为1cm,CB=3cm.求AD的长.
我登峰
11.如图,⊙O的直径AB=6cm,P是AB延长线上的一点,过点P作⊙O的切线,切点为C,连结AC.
(1)若∠CPA=30°,求PC的长;
(2)若点P在AB的延长线运动,∠CPA的平分线交AC于点M,∠CMP的大小会发生变化吗?若变化,请说明理由;若不变,请求出∠CMP的值。
3.2 三角形的内切圆
我预学
1. 如图,已知∠ABC.
(1)请用尺规作出∠ABC的角平分线;若点P为这条角平分线上的任意一点,则点P到AB、BC的距离有怎样的数量关系?
(2)在角的内部,满足到角两边BA、BC的距离相等的点在怎样的一条线上?
2. 如图,已知点△ABC .
(1)若求作一点P,使点P到线段AB、BC的距离相等,这样的点P你能作 个;
(2)求作一点P,使点P到△ABC三边的距离相等,这样的点P你能作 个,请你在图中用直尺和圆规作出点P.
3. 阅读教材中的本节内容后解答:
(1)本节内容有两个重要概念:三角形的内切圆和三角形的内心,请类比学习过的三角形的外接圆、三角形的外心,“内”与“外”是相对于什么定义的?你是怎么理解的?
(2)请比较三角形的外接圆和内切圆的作法,分别是怎么确定圆心和半径的,结合第2题中的图形加以说明.
(3)请猜想例2中线段AE和AF,CE和CD,BF和BD分别有怎样的数量关系?并证明你的猜想(结合第2题图).请你由此概括得出一个命题.
我求助:预习后,你或许有些疑问,请写在下面的空白处:
我梳理
我反思:通过本节课的学习,你一定有很多感想和收获,请写在下面的空白处:
我达标
1.若点P为△ABC内心,则( )
A.点P为三边中线的交点 B.点P为三边中垂线的交点
C.点P到三顶点的距离相等 D.点P到三边的距离相等
2.在△ABC中,I为内心,若∠A =70°,则∠BIC= ,若O为外心,则∠BOC= .
3.等边三角形的内切圆半径与外接圆半径之比为 .
4.如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9cm,BC=14cm,CA=13cm.则AF= ,BD= ,CE= .
5.如图,有一块三边分别为0.4m,0.5m和0.6m的三角形铝皮,怎样才能剪出一个面积最大的圆形铝皮?请你设计出裁剪方案,并在图中画出来(不要求写作法,但要保留作图痕迹).
6.如图,⊙O内切于△ABC,与AB,BC,CA分别相切于点D,E,F,∠DEF=50°,求∠A的度数.
7.已知:如图,在△ABC中,⊙O截△ABC的三边所得的弦长相等,求证:O是△ABC的内心.
我挑战
8.若三角形的三边之比为3∶4∶5,则它的内切圆与外接圆的半径之比为 .
9.如图,DE是△ABC的内切圆⊙O的切线,D,E分别在AB,AC上,已知BC=2,△ADE的周长是4,则△ABC的周长为 .
10.如图,⊙O是△ABC的内切圆,切点分别是D,E,F,AB=AC=10,BC=12,求:
(1)AD的长;
(2)△ABC的面积;
(3)⊙O的半径.
我登峰
11.如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,其内切圆⊙I分别切BC,AC,AB于点D,E,F.
(1)试说明:⊙I的半径r=(a+b-c);
(2)若BD和AE是方程x2-5x+6=0的两个根(BD
3.3圆与园的位置关系
我预学
1.如图,已知∠ABC=30°,点M在BC上,且BM=5cm,当r分别取下列值时,以M为圆心,r为半径的圆与直线BA分别有怎样的位置关系?
(1)r=2cm;
(2)r=4cm;
(3)r=2.5cm.
2.阅读教材中的本节内容后回答:
记两个圆的圆心距为d,两个圆的半径为R、r.
(1)在d、R、r、R+r、R-r五个量中,判断两个圆的位置关系时只需要关注哪三个量?
(2)当d< R+r时,两圆有怎样的位置关系?
(3)阅读教材的例题后你发现解决两圆相切问题最常用的辅助线是什么?
我求助:预习后,你或许有些疑问,请写在下面的空白处:
我反思:通过本节课的学习,你一定有很多感想和收获,请写在下面的空白处:
我达标
1.已知两圆的半径分别是2和4,圆心距是3,则这两圆的位置关系是( )
A.内含 B.内切 C.相交 D.外切
2.已知⊙O1的半径为3cm ,⊙O2 的半径为4cm,若⊙O1和⊙O2 相切,则这两个圆的圆心距为 ;若⊙O1和⊙O2 无公共点,则两圆的圆心距d的取值范围是 .
3.两个圆的圆心都是点O,半径分别是3cm和6cm,若⊙P与小圆外切,同时与大圆内切,则⊙P的半径为 ,若⊙M与小圆内切,同时与大圆也内切,则⊙M的半径为 .
4.若⊙O1的圆心坐标为(2,0),半径为1,⊙O2的.圆心坐标为(-1,0),半径为3,则这两圆的位置关系为 .
5.如图,⊙O的半径为4cm,点P是⊙O外一点,OP=6cm。作图并解答:
(1)以点P为圆心作⊙P与⊙O外切,则⊙P的半径是多少?
(2)以点P为圆心作⊙P与⊙O内切,则⊙P的半径是多少?
6.如图,⊙O1和⊙O2外切于点P,过点P的直线分别交⊙O1,⊙O2与A,B,已知⊙O1与⊙O 2的面积比为3∶2,求AP∶BP.
7.某市公园的一个雕塑,它是由三个直径为1m的圆两两相磊立在水平的地面上(如图),则雕塑的最高点到地面的距离是多少?
我挑战
8. 工人师傅在一个长为25cm,宽为18cm的矩形铁皮上,剪去一个和三边都相切的圆后,在剩余部分的铁皮上再剪出一个最大的圆,则这个最大圆的半径为 .
9.如图,半圆O的直径AB=4,与半圆O内切的动圆O1与AB相切于点M,设⊙O1的半径为y,AM长为x,则y关于x的函数关系式是 .
10.已知⊙O1和⊙O2的半径分别为1和3,且⊙O1和⊙O2外切,则在平面上,半径为4且与⊙O1和⊙O2都相切的圆有几个?请你画一画.若半径为5,且与⊙O1和⊙O2都相切的圆又可以画几个?
我登峰
11.已知Rt△ABC中,∠ABC=90°,AC=6,BC=8.
(1)如图,若半径为r1的⊙O1是Rt△ABC内切圆,求r1的值;
(2)如图,若半径为r2的两个等圆⊙O1和⊙O2外切,且⊙O1与AC,BA相切,⊙O2与BC,BA相切,求r2的值.
(3)请你类比问题(1)(2),拓展到Rt△ABC的内部有n个圆外切的情况,提出一个类似的问题,并解决你提出的问题.
3.1 直线与圆的位置关系(3)
1. 4 2. 120°3. 25° 4. ± 3 5.75° 6.略 7.4.8 8.(1)40° (2)70°或110° 9. 2 10. 11.(1)3 (2)45°
3.2 三角形的内切圆
1.D 2.125°140° 3.1∶2 4.AF=4cm,BD=5cm,CE=9cm 5.作△ABC的内切圆 6.80°7.略 8.2∶5 9.8 10.(1)4 (2)48 (3)3 11.(1)略 (2)BA=5,AC=4,BC=3 (3)
3.3圆与园的位置关系
1. C 2. 1cm或7cm d>7或0cm
