浙教版八上第六章图形与坐标全章学案

6.1 探索确定位置的方法
我预学
1.问题:①如果你拿到如下的电影票,你能找到自己的位置吗?
②假如你要找到自己的位置,还需加什么条件?
③如果换一张电影票,你能找到自己的位置吗?
④电影院里的座位是如何确定的?
2. 阅读教材内容后请回答：有序实数对（2，3）和（3，2）所表示的点有什么不同？
3. 阅读教材内容后请回答：你认为确定物体的位置有哪几种方法？
我求助：预习后，你或许有些疑问，请写在下面的空白处：
我梳理
个性反思：通过本节课的学习，你一定有很多感想和收获，请写在下面的空白处：
我达标
1．(1)在教室里从讲台开始从前往后、从左往右数你的位置是4排3座，用有序实数对记作 .
(2)做操时，小华的位置是第6行第3列，用有序实数对记作 .
2．(1)如图如果规定行写在前面，列号写在后面，则A点表示为( )
(A)(1， 2) (B)(2 ，1)
(C)(1 ，2)或(2 ，1) (D)以上都不对
(2)如上图小正方形边长表示1km，点A相对点B的位置表述正确的是( )
(A)北偏西450方向 (B)南偏东450方向
(C)北偏西450方向2km处 (D)南偏东450方向2km处
3．如果规定行写在前面，列号写在后面，试用数对的方法表示出图中各点的位置.

我挑战
4．某船从A港出发,先向正东行驶3千米到达B港，再向北航行3千米到达C港,求船只相对于A港的方位和距离
5．小兰上学路上看见小雪,她一口气追上小雪,对小雪说:“刚才你在我的北偏西300方向”.小雪说：“那你在我的西偏北300方向”. 小雪说得对吗？
我登峰
6． 某船上午8点观察到小岛在北偏东600方向，它以每小时20千米的速度向正东航行，上午10点观察到小岛在北偏东300方向，此时船离小岛的距离是多少千米.
6.2 平面直角坐标系(1)
我预学
1数轴上的点与 一一对应；
2.表示物体的位置的方法有哪几种？请你思考是否能找到一种方法使不同人表示的同一物体的位置的一对有序数对都一样呢？
3. 阅读教材内容后请回答：
在平面直角坐标系中，如何根据坐标描出点的位置，由点的位置写出它的坐标.

我求助：预习后，你或许有些疑问，请写在下面的空白处：
我梳理

个性反思：通过本节课的学习，你一定有很多感想和收获，请写在下面的空白处：
我达标
1.(1)平面直角坐标系中点A（0， 4）必在
(2)点A(1-)在第 象限
(3)若点(a ,2)在第二象限,且在两坐标轴的夹角平分线上,则a=
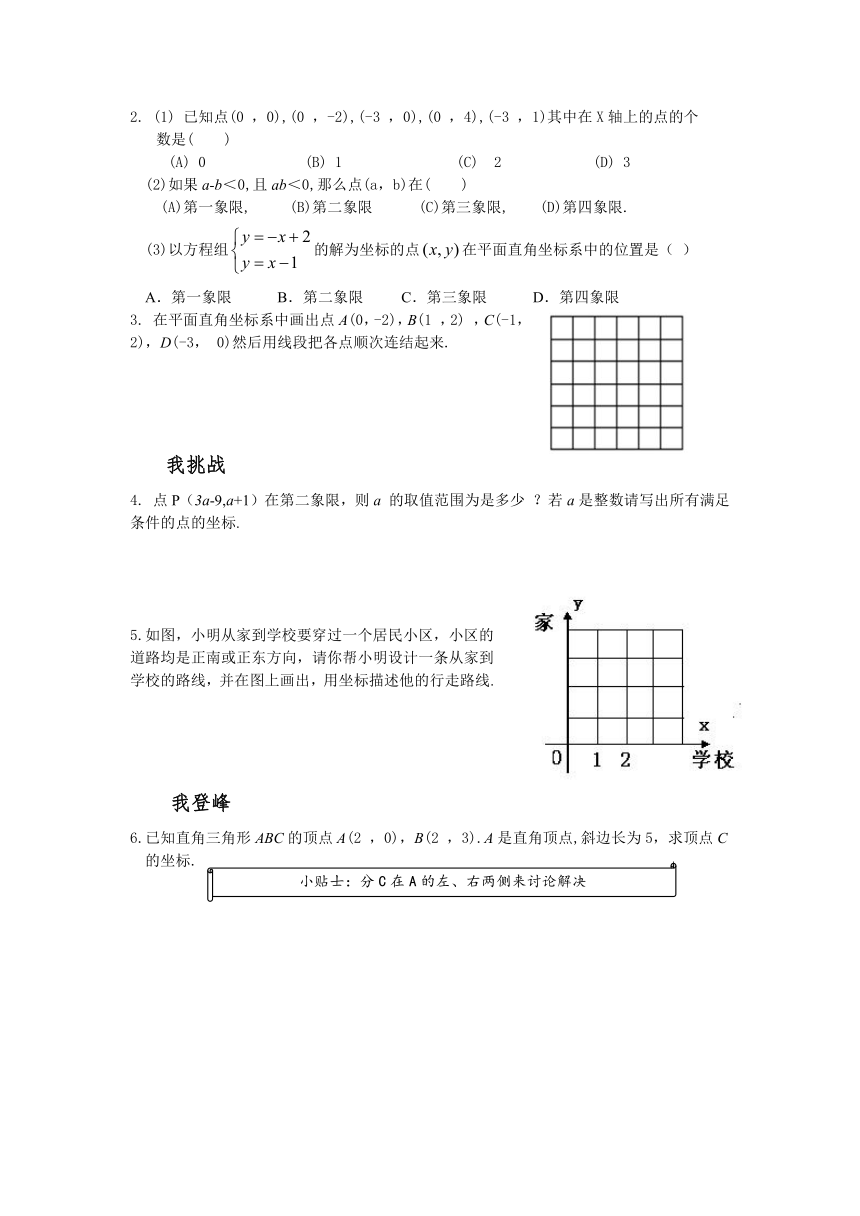
2. (1) 已知点(0 ，0),(0 ，-2),(-3 ，0),(0 ，4),(-3 ，1)其中在X轴上的点的个
数是( )
(A) 0 (B) 1 (C) 2 (D) 3
(2)如果a-b＜0,且ab＜0,那么点(a，b)在( )
(A)第一象限, (B)第二象限 (C)第三象限, (D)第四象限.
(3)以方程组的解为坐标的点在平面直角坐标系中的位置是（ ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
3. 在平面直角坐标系中画出点A(0，-2)，B(1 ，2) ，C(-1， 2)，D(-3， 0)然后用线段把各点顺次连结起来.
我挑战
4. 点P（3a-9,a+1）在第二象限，则a 的取值范围为是多少 ？若a是整数请写出所有满足条件的点的坐标.

5.如图，小明从家到学校要穿过一个居民小区，小区的道路均是正南或正东方向，请你帮小明设计一条从家到学校的路线，并在图上画出，用坐标描述他的行走路线.
我登峰
6.已知直角三角形ABC的顶点A(2 ，0)，B(2 ，3).A是直角顶点,斜边长为5，求顶点C的坐标.

6.2 平面直角坐标系(2)
我预学
阅读教材内容后请回答：
1．两条相交的数轴一定能组成平面直角坐标系吗？坐标平面内的每一个点的位置由________ ___来确定.
2．一条水平数轴上的点的坐标与平面直角坐标系中X轴上的点的坐标表示的形式一样吗？
3．坐标轴上的点有何特征？每个象限上的点有何特征？
我求助：预习后，你或许有些疑问，请写在下面的空白处：
我梳理
个性反思：通过本节课的学习，你一定有很多感想和收获，请写在下面的空白处：
我达标
1.(1)已知点A（m，n）在第四象限，那么点B（n，m）在第 象限
(2)若点P(3a-9,1-a)是第三象限的整数点(横、纵坐标都是整数)，那么a=
(3) 在直角坐标系中，若一个正方形，每个顶点到横轴、纵轴的距离都是6，则此正方形的四个顶点坐标分别为 .
(4) 已知点P（x2-3，1）在一、三象限夹角平分线上，则x= .
2.(1)如图，正三角形的边长为4，则点C的坐标是（ ）
(A)（4，-2） (B)（4，2）
(C)（，-2） (D)（-2，）
(2) 在x轴上，且到原点的距离为2的点的坐标是（ ）
(A) （2，0） (B) （-2，0） (C) （2，0）或（-2，0） (D) （0，2）
(3) 如果＜0，那么点P（x，y）在（ ）
(A) 第二象限 (B) 第四象限
(C) 第四象限或第二象限 (D) 第一象限或第三象限
3. 直角坐标系中，正三角形的一个顶点的坐标是（0，），另两个顶点B、C都在x轴上，求B，C的坐标.
4.直角坐标系中，一长方形的宽与长分别是6，8，对角线的交点在原点，两组对边分别与坐标轴平行，求它各顶点的坐标.
我挑战
5. 已知P(m,n)在第二象限，有序数对(m,n)中的整数m,n满足m-n=-6,写出所有符合条件的点坐标，并在平面直角坐标系中表示出来.
6.平面直角坐标系中，点P在第四象限，它到X轴的距离是3，它到Y轴的距离是4，则该点的坐标是（3，-4），你认为对吗？
我登峰
7.如图的围棋放置在某个平面直角坐标系内,白棋②的坐标为(-7，-4),白棋④的坐标为(-6，-8),求黑棋①的坐标.
6.3 坐标平面内的图形变换(1)
我预学
七年级我们学习了图形轴对称变换，图形轴对称变换过程中只改变图形的 ，不改变图形的 .
A是X轴上的一个点坐标为（5，0），则A点关于Y轴对称点B的坐标是 ；若A点坐标为（5，3）呢？
3. 阅读教材内容后请回答：
关于x轴对称的点、关于y轴对称的点的坐标有什么规律？

我求助：预习后，你或许有些疑问，请写在下面的空白处：
我梳理
个性反思：通过本节课的学习，你一定有很多感想和收获，请写在下面的空白处：
我达标
1.(1)点P（-2，4）关于x轴对称的点的坐标是
(2)点A关于y轴对称的点的坐标是（4，-5），则点A的坐标是 .
(3)已知点A（a，-3），B（4，b）关于y轴对称，则a-b= .
(4)已知P（2，-3）关于x轴对称的点是P1，P1关于y轴对称的点是P2，则P2的坐标是 .
2.(1)点A（0，-4）与点B（0，4）是（ ）
(A) 关于y轴对称 (B) 关于X轴对称 (C)关于坐标轴对称 (D) 不能确定
(3)点P在第四象限，且，则点P关于x轴对称点的坐标是（ ）
(A)（3，-5） (B)（-3，5） (C)（-5，-3） (D)（3，5）
3. 如图，圆O1的圆心在x轴上，半径是5，OO1=3，写出圆与各坐标轴交点的坐标，点A与点B的坐标有什么关系？
我挑战
4. 如图，梯形OABC是正六边形的一部分，画出它关于x轴对称的其余部分，如果AB的长为2，求出各顶点的坐标.
5. 在平面直角坐标系中, △ABC的三个顶点的位置如图所示， 作出△ABC关于x轴对称的象,使点A变换为点A', 点B′、C′分别是B、C的对应点.
（1）请画出像△A'B'C'（不写画法) ，并直接写出点B′、C′的坐标:
B′（ ）、 B′（ ）、C′ （ ） ；
（2）若△ABC 内部一点P的坐标为（a,b），则点P　的对应点P ′的坐标是 （ ） .

我登峰
6.在平面直角坐标系中，将坐标是（-5，0），（-4，-2），（-3，0），（-2，-2），（-1，0）的点用线段依次连接起来，形成图案I，
（1）作出该图案关于y轴对称的图案II；
（2）将所得的图案II沿x轴向上翻折180°后得到一个新的图案III，试写出它的各顶点坐标；
（3）观察图案I与III，比较各自顶点的坐标和图案位置，你能得到什么结论？
6.3 坐标平面内的图形变换(2)
我预学
1.七年级我们学习了图形平移变换，图形平移变换过程中只改变图形的 ，不改变图形的 .
2. 阅读教材内容后请回答：点左右平移、上下平移时坐标有什么规律？
我求助：预习后，你或许有些疑问，请写在下面的空白处：
我梳理
个性反思：通过本节课的学习，你一定有很多感想和收获，请写在下面的空白处：
我达标
1.(1)点A（-2，4）向左平移3个单位的象的坐标是 .
(2)点A（2，1）向右平移5个单位，再向下平移3个单位的象的坐标是 .
(3)点P（-2，0）向 平移 个单位，则向 平移 个单位的象的坐标是（3，-1）
2.(1) 点A（3，-4）向左平移3个单位的象的坐标是（ ）
(A)（6，-4） (B)（0，-4） (C)（3，-1） (D)（3，-7）
(2)点M（-5，y）向下平移5个单位的象关于x轴对称，则y的值是（ ）
(A)-5 (B)5 (C) (D)-
(3)把点P（-x，y）变为Q（x，y），只需（ ）
(A) 向左平移2x个单位 (B) 向右平移2x个单位
(C) 作关于x轴对称 (D) 作关于y轴对称
3．已知A，B两点是平面直角坐标系内不同的两点，A（x，3），B（4，y），如果AB∥x轴，求x，y的值.
4.如图所示是一艘船在平面直角坐标系内的位置，
（1）写出图中所标出的各个点的坐标；
（2）如果船朝东航行6个单位长度，再向北平移4个单位长度，则变化后船所在位置的各点坐标为怎样？
我挑战
5.如图，作△ABC关于x轴对称的像，然后把像向下平移3个单位，求此时三角形各顶点的坐标.

6.我们知道点P(x,y)关于X轴的对称点坐标是(x,-y),点P(x,y)关于Y 轴的对称点坐标是(-x,y),类似地可以得到点P(x,y)关于原点的对称点的坐标是(-x,-y),你能说明这条规律吗?并求出点(m,n)分别关于X轴、Y轴、原点的对称点的坐标.
我登峰
7.已知点P的坐标是(-4 ，3),先将点P作X轴的轴对称变换得点P1，再将P1作平移变换,向右平移8个单位得P2,则PP2的距离是10.你认为对吗?说明你的理由.
6.1 探索确定位置的方法
1.（1）略（2）（6，3） 2.（1）A（2）D 3.略 4.北偏东450相距3米处； 5. 错 6.40千米
6.2平面直角坐标系(1)
1.（1）y轴上（2）二（3）-2 2.（1）C（2）B（3）A 3.略 4.略 5. 略 6.（-2，0）、（6，0）
6.2平面直角坐标系(2)
1.（1）二（2）2（3）（6，6）、（-6，6）、（-6，-6）、（6，-6）（4）±2 2.（1）C（2）C（3）C 3.（-1，0）、（1，0）4.（-3，4）、（-3，-4）、（3，-4）、（3，4）或（-4，3）、（-4，-3）、（4，-3）、（4，3）5.(-5,1) 、(-4,2) 、(-3,3) 、(-2,4) 、(-1,5) 6. 错，（4，-3）7.（-3，-7）
6.3坐标平面内的图形变换(1)
1.（1）（-2，-4）（2）（-4，-5）（3）-1 （4） (-2,3) 2.（1）B（2）D 3.A（0，4）C（-2，0），B（0，-4）D（8，0）A、B关于x轴对称 4.A(1, ) B(3, )、C(4，0)、D（3，-）、E（1，-））O（0，0） 5. 略 6. （1）略（2）略2（3）关于原点成中心对称
6.3坐标平面内的图形变换(2)
1. 1（1）（-5，4）（2）（7，-2）（3）左5下1 2（1）B（2）C（3）D 3.x≠4,y=3 4. 略 5.A（-3，-1）、B（-2，-3）、C（0，-3） 6（m，-n）、（-m，n）、（-m，-n）7:对