浙教版八上第七章一次函数全章学案

第7章 一次函数
7.1 常量与变量
我预学
1.小明去文具店买某种笔，已知该笔2元/支，小明买了该种笔n支，应付钱为m元．
(1) 请写出m、n满足的关系；
(2) 填写下表：
练习本n（本）
1
2
5
8
…
付钱m（元）
…
(3) 在计算上述买了不同支数的笔应付的钱的过程. 哪些量在改变，哪些量不变？
2. 阅读教材中的本节内容后回答：
汽车行驶的路程S、行驶时间t和行驶速度v之间有下列关系：S=vt.
(1)如果汽车以60km/h的速度行驶，那么在S=vt中，变量是 ，常量是 ；如果汽车行驶的时间t规定为1小时，那么在S=vt中，变量是 ，常量是 ；(3)如果甲乙两地的路程S为200km，汽车从甲地开往乙地，那么在S=vt中，变量是 ，常量是 .
(2)根据以上三句叙述，写出一句关于常量与变量的结论，并再举一个符合你的结论的实际例子.
我求助：预习后，你或许有些疑问，请写在下面的空白处：
我梳理
区别
请举一例（不能与书本例子重复）
常量
在一个过程中， 的量称为常量
变量
在一个过程中， 的量称为变量
个性反思：通过本节课的学习，你一定有很多感想和收获，请写在下面的空白处：
我达标
1．正方形的面积S与边a之间的关系式为 ，其中变量是 .
2．在△ABC中，它的底边是a，底边上的高是h，则三角形的面积 .
当底边上的高h的长一定时，在关系式中的常量是 ，变量是 ；
当△ABC的面积S一定时，在关系式中的常量是 ，变量是 .
3．齿轮每分钟120转，如果表示转数，表示转动时间.
(1) 用的代数式表示；(2) 说出其中的变量与常量．
4．海水受日月的引力而产生潮汐现象. 早晨海水上涨叫做潮，黄昏海水上涨叫做汐，合称潮汐. 潮汐与人类的生活有着密切的联系. 某港口某天从0时到12时的水深情况如下表，其中T表示时刻，h表示水深：
T(时)
0
3
6
9
12
h(米)
5
7.4
5.1
2.6
4.5
上述问题中，字母T，h表示的是变量还是常量，简述你的理由.
我挑战
5．阅读下面这段有关“龟兔赛跑”的寓言故事，并指出所涉及的量中, 哪些是常量, 哪些是变量.
一次乌龟与兔子举行500米赛跑，比赛开始不久，兔子就遥遥领先. 当兔子以20米/分的速度跑了10分时，往回一看，乌龟远远地落在后面呢!兔子心想：“我就是睡一觉,你乌龟也追不上我,我为何不在此美美地睡上一觉呢?”可是，当骄傲的兔子正做着胜利者的美梦时，勤勉的乌龟却从它身边悄悄爬过，并以10米/分的速度匀速爬向终点. 40分后，兔子梦醒了，而此时乌龟刚好到达终点. 兔子悔之晚矣，等它再以30米/分的速度跑向终点时，它比乌龟足足晚了10分.
6．某电信公司提供了一种移动通讯服务的收费标准,如下表：
项目
月基本服务费
月免费通话时间
超出后每分收费
标准
40元
150分
0.6元.
则每月话费y (元)与每月通话时间x(分)之间有关系式，在这个关系式中，常量是什么?变量是什么?
7.2认识函数(1)
我预学
1. (1)寄一明星片的邮资为0.80元，寄x张这种明星片的总邮资为y元.
①请用x的代数式表示y；
②请分别求出x为2，3，5时，相应的y值是多少？
(2)某公司2011年年终财务报表显示，该公司2011年年终每股净利润为5元. 年报公布后的某日，该公司的股票收盘价为x元，所以这天收盘后该股票的市盈率为.请分别求出x为10，12，15时，相应的y值是多少？
(3) 请你概括出(1)、(2)小题中两个变量x，y之间的关系的共同点.
2. 阅读教材中的本节内容后回答：
在某个变化过程中，有两个变量x与y，能否说成y是x的函数？并说出你的判断理由.
(1)y=x2；(2)y2=x.
我求助：预习后，你或许有些疑问，请写在下面的空白处：
我梳理
个性反思：通过本节课的学习，你一定有很多感想和收获，请写在下面的空白处：
我达标
1．某中学要在校园内划出一块面积是 100m2的长方形土地做花圃，设这个矩形的相邻两边的长分别为xm和ym. 则y关于x的函数解析式为 ；当x=10时的实际意义是 .
2．当时函数的值为 .
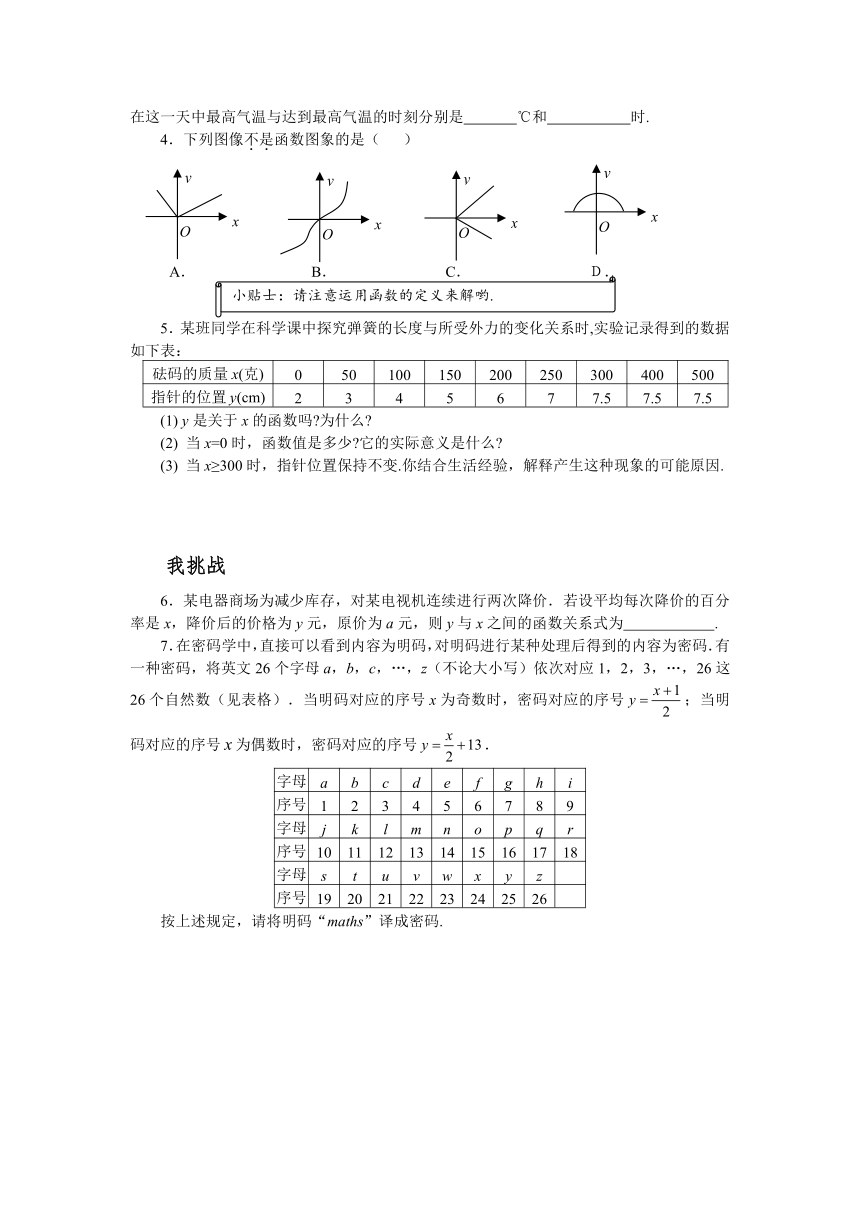
3．如图是某地一天的气温随时间变化的图象，根据图象可知，在这一天中最高气温与达到最高气温的时刻分别是 ℃和 时.
4．下列图像不是函数图象的是（ ）
5．某班同学在科学课中探究弹簧的长度与所受外力的变化关系时,实验记录得到的数据如下表：
砝码的质量x(克)
0
50
100
150
200
250
300
400
500
指针的位置y(cm)
2
3
4
5
6
7
7.5
7.5
7.5
(1) y是关于x的函数吗?为什么?
(2) 当x=0时，函数值是多少?它的实际意义是什么?
(3) 当x≥300时，指针位置保持不变.你结合生活经验，解释产生这种现象的可能原因.
我挑战
6．某电器商场为减少库存，对某电视机连续进行两次降价．若设平均每次降价的百分率是x，降价后的价格为y元，原价为a元，则y与x之间的函数关系式为 .
7．在密码学中，直接可以看到内容为明码，对明码进行某种处理后得到的内容为密码．有一种密码，将英文26个字母a，b，c，…，z（不论大小写）依次对应1，2，3，…，26这26个自然数（见表格）．当明码对应的序号x为奇数时，密码对应的序号；当明码对应的序号为偶数时，密码对应的序号．
字母
a
b
c
d
e
f
g
h
i
序号
1
2
3
4
5
6
7
8
9
字母
j
k
l
m
n
o
p
q
r
序号
10
11
12
13
14
15
16
17
18
字母
s
t
u
v
w
x
y
z
序号
19
20
21
22
23
24
25
26
按上述规定，请将明码“maths”译成密码.
7.2认识函数(2)
我预学
1. (1)若分式有意义，则x的取值范围是 . 要使分式有意义，必须满足条件 .
(2)要使形如算术平方根（二次根式）的代数式的意义，则x的取值范围是 . 要使算术平方根（二次根式）有意义，必须满足条件 .
2. 阅读教材中的本节内容后回答：
(1)例1中求x的取值范围时，为什么要满足“x>0，y>0，2x>y”？请说出你的理由；
(2)例2中的自变量t的取范围又是怎样求出来的（即满足哪些条件？）.
(3)结合例1、例2，请说说求实际问题中自变量的取值范围时，可从哪几个方面去考虑？
我求助：预习后，你或许有些疑问，请写在下面的空白处：
我梳理
函数式名称
自变量x的取值范围
整式函数式：=ax+b(a≠0)
分式函数式：(a≠0)
算术平方根（二次根式）函数式：(a≠0)
a>0时：
a<0时：
个性反思：通过本节课的学习，你一定有很多感想和收获，请写在下面的空白处：
我达标
1．在函数中，自变量的取值范围是 .
2．有一个面积为30的梯形，其下底长是上底长的3倍. 若设上底长为x，高为y，则y关于x的函数解析式是 .
3．等腰三角形顶角的度数y与底角的度数x之间的函数关系式为 ，x的取值范围是 .
4．现有一根金属棒，在0℃时的长度是200cm，温度每升高1℃，它就伸长0.002cm.则求这根金属棒的长度l与温度t的函数关系式为 ，当温度为100℃时，这根金属棒的长度为 cm.
5．两个变量y与x之间的函数图象如图所示，则自变量x的取值范围是__ _.
6．商店在出售某商品时，在进价的基础上增加一定的利润，其数量x与售价y 之间的关系如下表所示：
数量x(千克)
1
2
3
4
…
售价y（元）
8+0.4
16+0.8
24+1.2
32+1.6
…
(1) 请根据表中提供的信息，写出y与x的函数关系式；
(2) 当x取何值时，售价为126 元？
7．已知三角形的三边长分别为10cm，7cm，xcm，它的周长为ycm.
(1)求y关于x的函数解析式和自变量的取值范围；
(2)当x=6cm时，求三角形的周长；
(3) 当x=18cm时，能求出三角形的周长吗?为什么?
我挑战
8．在函数中，自变量的取值范围是 .
9．某中学环保兴趣小组对公园中正在清除湖泊中淤泥的工人进行调查，并从调查中收集到下列数据：
湖泊面积（单位：米2）
淤泥平均厚度（单位：米）
每天清淤泥量（单位：米3）
150
0.7
5
设清除淤泥x天后，剩余的淤泥量为y (米3)，则y与x的函数关系为 ，若为了使湖泊中的生物链不遭破坏，仍需保留约30米3的淤泥. 若需保留的淤泥量，则除淤泥需 天才能完工.
10．小明家于2009年2月份买了一套房，当时（即2月份）在银行借了54万元住房贷款，贷款期限为15年，从开始贷款的下一个月起逐月偿还，贷款月利率是0.5%，每月还款数额=平均每月应还的贷款本金数额+月利息，月利息=上月所剩贷款本金数额×月利率.
(1)求小明家借款后第一个月应还款数额；
(2)假设贷款月利率不变，请写出张老师借款后第n（n是正整数）个月还款数额p与n之间的函数关系式；
(3)在(2)的条件下，求小明家2011年12月份应还款数额.
我登峰
11．如图，长方形ABCD中，AB=4cm，BC=5cm．点P从A点开始以1cm/s的速度向D点运动，设点P运动的时间为t(s)，阴影部分的面积为S．
(1)求阴影部分的面积S与t之间的函数解析式和自变量t的取值范围；
(2)当△BCP为等腰三角形时，求阴影部分的面积.
7.3一次函数(1)
我预学
1.求出下列各题中的y与x之间的关系式：
(1)正方形的周长y与边长x之间的函数关系式： ；
(2)长方形的周长为10，两条边长分别为x，y，则y与x之间的函数关系式为 ；
(3)某工厂现在年产值是50万元，计划今后每年增加2万元，则年产值y（万元）与年数x的函数关系式为 .
2.比较第1题中的三个函数，说说它们有哪些共同特征？
3.阅读教材中的本节内容后回答：
为什么教材中一次函数的解析式和正比例函数的解析式中都必须有“k≠0”这个条件？
我求助：预习后，你或许有些疑问，请写在下面的空白处：
我梳理
个性反思：通过本节课的学习，你一定有很多感想和收获，请写在下面的空白处：
我达标
1．已知一次函数y=-2x+m，当x=1时， y=2，则m= .
2．一次函数y=-2(x+1)-3x的常数项b= .
3．若函数y= -2xm+2是正比例函数，则m的值是 .
4．某下岗职工购进一批香蕉，到集贸市场零售，已知卖出的香蕉数量x与售价y的关系如下表所示：
数量x（千克）
1
2
3
4
5
售价y（元）
2+0.1
4+0.2
6+0.3
8+0.4
10+0.5
则y与x的函数关系式是 ，这是 函数.
5．下列说法错误的是（ ）
A. 一次函数不一定是正比例函数 B. 不是一次函数就一定不是正比例函数
C. 正比例函数是特殊的一次函数 D. 不是正比例函数就一定不是一次函数
6．已知y是x的正比例函数，当x=-3时，y=12.
(1) 求y关于x的函数解析式；
(2) 当时的函数值；
(3) 当y<8时，求x的取值范围.
7．写出下列各题中y与x的函数关系式，并判断y是否是x的一次函数或正比例函数？
(1) 某种储蓄的月利率是0.2％（免利息税），存入100元本金后，利息y（元）与所存月数x之间的函数关系式；
(2) 某服装厂承揽一项生产T恤衫1600件的任务，计划用t天完成. 每天生产T恤衫w（件）与生产时间t（天）（t＞4）之间的函数关系式；
(3) 有一个水箱，它的容积为500升，水箱内原有水200升，现需将水箱注满，已知每分种注入水10升. 水箱内水量Q（升）与时间t（分）的函数关系式.
我挑战
8．已知函数y=(k-1)x|k|+3是一次函数，则x=k时，y的值为 .
9．为了增强农民抵御大病风险的能力，政府积极推行农村医疗保险制度．我市某县根据本地的实际情况，制定了纳入医疗保险的农民住院医疗费用的报销规定：享受医保的农民可在定点医院住院治疗，由患者先垫付医疗费用，住院治疗结束后凭发票到县医保中心报销．住院医疗费用的报销比例标准如下表：
费用范围
100元以下（含100元）
100元以上的部分
报销比例标准
不予报销
(1)设某位享受医保的农民在一次住院治疗中的医疗费用为x元（x>100），按规定报销的医疗费用为y元，试写出y与x的函数关系式；
(2)若该农民在这次住院治疗中的医疗费用为1000元，则他在这次住院治疗中自负的医疗费用为多少元．
10．为了增强居民的节约用水的意识，某市制定了新的水费标准：每户每月用水量不超过5吨的部分，自来水公司按每吨2元收费；超过5吨的部分，按每吨2.6元收费. 设某用户月用水量x吨，自来水公司的应收水费为y元.
(1)试分别写出x≤5和x>5时，y（元）与x（吨）之间的函数关系式；
(2)该户今年5月份的用水量为8吨，自来水公司应收水费多少元？
我登峰
11．如图，长方形ABCD中，当点P在从A开始以2cm/s的速度沿着折线AB—BC—CD向D移动，若长方形的长AD=6cm，宽AB=4cm，设点P运动的时间为t(s)，PB的长为ycm，△PAD的面积为Scm2.
(1)请分别写出点P分别在线段AB上、线段BC上、线段CD上时，S与x之间的函数关系式，并指出相应的自变量x的取值范围；
(2)分别求P分别在线段AB上、线段BC上时，y与x之间的函数关系式；
(3)分别求t=3，6时PB的长.
7.3一次函数(2)
我预学
1.已知函数 y=kx+b. 当k ，b 时是一次函数；当k ，b 时是正比例函数.
2. 已知y与x成正比例，且x=2时，y=-6，求y与x的函数关系式，请你用自己的语言说说求函数解析式的基本步骤.
3.阅读教材中的本节内容后回答：
为什么教材中例3的第(1)小题可用一次函数来描述该地区沙漠面积的变化？
我求助：预习后，你或许有些疑问，请写在下面的空白处：
我梳理
用待定系数法求一次函数解析式的基本步骤：
1．设．设所求的一次函数的解析式为 （其中k、b为待确定的常数）；
2．代．把 对已知的自变量与函数值代入解析式，得关于k、b的 ；
3．解．解关于k、b的 ，求出k、b的值；
4．写．将求出k、b的值代入 ，得所求一次函数的解析式．
个性反思：通过本节课的学习，你一定有很多感想和收获，请写在下面的空白处：
我达标
1．已知一次函数y=-3x+b，当x=1时，y=-2，那么b的值是_______.
2．若y与x成正比例，且当时，y=2，则当时，x的值是___________.
3．若已知一次函数y=3x-6，则当x<0时，y的取值范围为 .
4．下表列出了一项试验统计数据，表示将皮球从高处h米落下时，弹跳高度S米与下落高度d的关系．能表示这种关系的解析式为 .
h（米）
50
80
100
150
S（米）
25
40
50
75
5．下列各题：①汽车以60千米/时的速度行驶，行驶路程y(千米)与行驶时间x（时）之间的关系；②圆的面积y(cm2)与它的半径x(cm)之间的关系；③一棵树现在高50cm，每个月长高2cm，x月后这个棵树的高度为y(cm). 其中y是x的一次函数的为 .(填序号).
6．已知y是x的一次函数，且当x=0时，y=2；当x=1时，y=-1. 求y关于x的函数解析式.
7．如图，两摞相同规格的饭碗整齐地叠放在桌面上，请根据图中给的数据信息，解答下列问题：
(1)求整齐摆放在桌面上饭碗的高度y(cm)与饭碗数x(个)之间的一次函数解析式；
(2)把这两摞饭碗整齐地摆成一摞时，这摞饭碗的高度是多少？
我挑战
8．已知y与2x+1成正比例，且x=-1时，y=2，则y与x的函数解析式为 .
9．设m、n(m≠0)为常数，如果正比例函数y=kx中，自变量x增加m，对应的函数y增加n，那么k的值是（ ）
A. B.
C. D.
10．2010年我国西南地区遭受了百年一遇的旱灾，但在这次旱情中，某市因近年来“森林城市”的建设而受灾较轻．据统计，该市2009年全年植树5亿棵，涵养水源3亿立方米，若该市以后每年年均植树5亿棵，到2015年“森林城市”的建设将全面完成，那时，树木可以长期保持涵养水源11亿立方米．
(1) 从2009年到2015年这七年时间里，该市一共植树多少亿棵?
(2) 若把2009年作为第l年，设树木涵养水源的能力y(亿立方米)与第x年成一次函数，求出该函数的解析式，并求出到第3年(即2011年)可以涵养多少水源?
我登峰
11．已知y+m与t+n(其中m、n是常数)成正比，t是x的一次函数．
(1) y是t的一次函数吗？说明理由；
(2) y是x的一次函数吗？说明理由；
(3)若x=3时，y=5；x=2时，y=2，求函数的表达式.
7.4一次函数的图象(1)
我预学
1.请画一个平面直角坐标系，并指出各象限和坐标系上点的特征.
2. 已知y与x有如下关系：
x
…
-2
-1
0
1
2
…
y
…
3
1
-1
-3
-5
…
(1)请写出y关于x的一次函数关系式： ；
(2)请把上表中x的值作为点的横坐标，y的值作为纵坐标，并在第1题的坐标系中描出来；
(3)我们将这些点依次用线段连接起来，可发现这些点在位置上有什么特征？
3.阅读教材中的本节内容后回答：
我们知道一次函数的图象只要过其中两个点即可，但如果这两个点一旦有分数出现，往往描点时不够准确；如果数值过大，则坐标系过大，不够经济. 为避免以上问题，你认为如何取这两个点？请写下你的想法.
我求助：预习后，你或许有些疑问，请写在下面的空白处：
我梳理

个性反思：通过本节课的学习，你一定有很多感想和收获，请写在下面的空白处：
我达标
1．如果点P(-1，5)在正比例函数y=kx的图象上，那么k= .
2．直线y=-x+3与x轴的交点坐标是 ，与y轴的交点坐标是 .
3．点(m，2)在直线y=3x-4，则m的值为 .
4．写出正比例函数y=3x与的两条共同点是 .
5．直线y=-3x+2的图象不经过第 象限.
6．画出直线y=2x-6的图象，试判断点（m+1，2m-4）是否在这条直线上？
7．已知一次函数的图象过M(1，3)，N(-2，12)两点. 求函数的解析式.
我挑战
8．我们知道直线y=2x-6的图象是一条直线. 当x≥3时，它的图象是一条 ；当3≤x≤10时，它的图象是一条 .
9．如图，直线与x轴、y轴分别交于A、B两点，则△AOB的面积是 ，把△AOB绕点A顺时针旋转90°后得到△AO′B′，则点B′的坐标是 .
10．已知正比例函数y=kx经过点P(1，2），如图所示．
(1)求这个正比例函数的解析式；
(2)将这个正比例函数的图像向右平移4个单位，写出在这个平移下，点P、原点O的像P′、O′的坐标，并求出平移后的直线的解析式；
(3)求这两条直线之间的距离.
我登峰
11．我国青海省玉树地区发生强烈地震以后，国家立即启动救灾预案，积极展开向灾区运送救灾物资和对伤员的救治工作．已知西宁机场和玉树机场相距800千米，甲、乙两飞机沿同一航线各自从西宁、玉树出发，相向而行．如图，线段AB、CD分别表示甲、乙两机离玉树机场的距离S（百千米）和所用去的时间t（小时）之间的函数关系的图象（注：为了方便计算，将平面直角坐标系中距离S的单位定为（百千））．观察图象回答下列问题：
(1)乙机在甲机出发后几小时，才从玉树机场出发？甲、乙两飞机的飞行速度每小时各为多少千米？
(2)求甲、乙两机各自的S与t的函数关系式；
(3)求P点坐标，并说明它的实际意义.
7.4一次函数的图象(2)
我预学
1.请在同一坐标系内画出y=x-2与y=-x-2的图象.
2. 在第1题的两个函数的图象上任取几点，当点的横坐标增大时，观察它们的纵坐标分别有怎样的变化？试着再举几个例子验证你的猜想.
3.阅读教材中的本节内容后回答：
如何理解一次函数性质中“y随x的增大而增大或y随x的增大而减小”？请指出这个性质在例2、例3中是如何体现的？
我求助：预习后，你或许有些疑问，请写在下面的空白处：
我梳理
一次函数的定义
形如y=kx+b(k，b都是常数，且 )的函数叫做一次函数.
一次函数的图象
k>0，b>0
经过一、二、三象限
一次函数的性质
k>0
k<0
y随x的增大而
y随x的增大而
个性反思：通过本节课的学习，你一定有很多感想和收获，请写在下面的空白处：
我达标
1．一次函数y=x-100中，y随着x的增大而 .
2．若一次函数y=kx+b的图象经过两点（0，-5a2）和（-5a2，0），则k的取值范围是 ．
3．点(x1，y1)、(x2，y2)在直线y=3x-4上，若x1<04．已知函数y=x+3，其中-2≤x≤10，则y的最大值为 ，最小值为 .
5．一次函数具有下列性质：①图像经过点（1，-2），（3，m）；②m<-2．满足上述两条性质的函数解析式可以是 （只要求写一个）．
6．一次函数经过（1，-1），（-2，2）两点，试求当-37．已知某种商品的进价为168元，售价的10%用于缴税和其它费用.
(1)设商品的售价为x元，纯利润为y元，求y关于x的函数解析式；
(2)若要使纯利润保持在售价的10%~20%之间(包括10%和20%)，问怎么确定售价?
我挑战
8．一次函数y=(m+4)x+2m-1，如果y随x增大而增大，且它的图象与y轴的交点在x轴下方，则m的取值范围 .
9．已知某函数图象关于直线x=1对称，其中一部分图象如图所示，点A(x1，y1)，点B(x2，y2)在函数图象上，且-1A. y1>y2 B. y1=y2 C. y110．某酒厂每天生产A、B两种品牌的白酒共600瓶，A、B两种品牌的白酒每瓶的成本和利润如下表：
设每天生产A种品牌的白酒x瓶，每天获利y元.
(1)请写出y关于x的函数关系式；
(2)如果该酒厂每天至少投入成本26400元，那么每天至少获利多少元？
我登峰
11石化乙烯厂某车间生产甲、乙两种塑料的相关信息如下表，请你解答下列问题：
出厂价
成本价
排污处理费
甲种塑料
2100（元/吨）
800（元/吨）
200（元/吨）
乙种塑料
2400（元/吨）
1100（元/吨）
100（元/吨）
每月还需支付设备管理、
维护费20000元
(1)设该车间每月生产甲、乙两种塑料各x吨，利润分别为y1元和y2元，分别求y1和y2 与x的函数关系式（注：利润=总收入-总支出），并在同一坐标系内画出图象；
(2)已知该车间每月生产甲、乙两种塑料均不超过400吨，若某月要生产甲、乙两种塑料共700吨，求该月生产甲、乙塑料各多少吨，获得的总利润最大？最大利润是多少？
7.5一次函数的简单应用(1)
我预学
1. 通过实验获得x，y两个变量的各对应值如下表：
(1)
x
0
0.5
1
1.5
2
2.5
3
4
y
1
2
3
4
5
6
7
8
判断变量x，y是否满足一次函数关系式，如果是，请求出解析式.
(2)
x
0
0.5
1
1.5
2
2.5
3
4
y
1
2.1
3.1
4.1
5.2
5.8
7.3
8.3
判断变量x，y是否近似满足一次函数关系式，请说出你的判断依据.
2.阅读教材中的本节内容后回答：
例1中为什么要选择（1.91，10.25），（2.59，12.50）这两点代入y=kx+b，这样选择的好处是什么？能否选择其他的两组点代入？
我求助：预习后，你或许有些疑问，请写在下面的空白处：
我梳理
求一次函数解析式的基本步骤
函数建模的基本步骤
1．设解析式；
2．把两对已知的自变量与函数值代入解析式；
3．解关于k、b的方程组；
4．写出一次函数的解析式．
1．通过实验、测量获得数量足够多的
的对应值；
2．建立合适的直角坐标系, 在坐标系内以各对应值为坐标描点, 并用
法画出函数图象；
3．观察图象特征，判定函数的 ；
4．用 法求出函数解析式.
个性反思：通过本节课的学习，你一定有很多感想和收获，请写在下面的空白处：
我达标
1．弹簧的长度与所挂物体的质量的关系为一次函数，如图所示，由图可知不挂物体时弹簧的长度为 cm.
2．在某次实验中，测得两个变量m和v之间的4组对应数据如下表：
m
1
2
3
4
v
0.01
2.9
8.03
15.1
则m与v之间的关系最接近于下列各关系式中的（ ）
A. v=2m-2 B. v=m 2-1 C．v=3m-3 D. v=m+1
3．假定甲、乙两人在一次赛跑中，路程s与时间t的关系如图所示，那么可以知道：（1）这是一次 米赛跑；（2）甲乙两人中先到达终点的是 ；（3）乙在这次赛跑中的速度为 米/秒.
4．如图所示，是某学校一电热淋浴器水箱的水量y（升）与供水时间x（分）的函数关系．
(1)求y与x的函数关系式；
　 (2)在(1)的条件下，求在30分钟时水箱有多少升水？
5．对于气温，有的地方用摄氏温度表示，有的地方用华氏温度表示，摄氏温度与华氏温度之间存在着某种函数关系，从温度计的刻度上可以看出，摄氏（℃）温度与华氏（°F）温度有如下对应关系：
x℃
…
-10
0
10
20
30
…
y°F
…
14
32
50
68
86
…
(1)通过①描点连线；②猜测与之间的函数关系；③求解；④验证等几个步骤，试确定y与x之间的函数关系；
(2)某天，南昌的最高气温是8℃，澳大利亚悉尼的最高气温是91°F，问这一天悉尼的最高气温比南昌的最高气温高多少摄氏度（结果保留整数）.
我挑战
6．一个水池有2个速度相同的进水口，1个出水口，单开一个进水口每小时可进水10立方米，单开一个出水口每小时可出水20立方米. 某天0点到6点，该水池的蓄水量与时间的函数关系如图所示(至少打开一个进水口). 给出以下三个论断：①0点到3点只进水不出水；②3点到4点不进水只出水；③4点到6点不进水也不出水. 则错误的论断是______________(填序号).
7．“震灾无情人有情”，玉树地震牵动了全国人民的心，武警某部队接到命令，运送一批救灾物资到灾区，货车在公路A处加满油后，以每小时60千米的速度匀速行驶，前往与A处相距360千米的灾区B处．下表记录的是货车一次加满油后油箱内余油量y（升）与行驶时间x（时）之间关系：
行驶时间x（时）
0
1
2
3
4
余油量y（升）
150
120
90
60
30
(1)请你用学过的函数中的一种建立y与x之间的函数关系式，说明选择这种函数的理由；（不要求写出自变量的取值范围）
(2)如果货车的行驶速度和每小时的耗油量都不变，货车行驶4小时后到达C处，C的前方12千米的D处有一加油站，那么在D处至少加多少升油，才能使货车到达灾区B处卸去货物后能顺利返回D处加油？（根据驾驶经验，为保险起见，油箱内余油量应随时不少于10升）
我登峰
8．一辆快车从甲地驶往乙地，一辆慢车从乙地驶往甲地，两车同时出发，匀速行驶.设行驶的时间为x(时)，两车之间的距离为y(千米)，图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系．
(1)根据图中信息，求线段AB所在直线的函数解析式和甲乙两地之间的距离；
(2)已知两车相遇时快车比慢车多行驶40千米，若快车从甲地到达乙地所需时间为t时，求t的值；
(3)若快车到达乙地后立刻返回甲地，慢车到达甲地后停止行驶，请你在图中画出快车从乙地返回到甲地过程中y关于x的函数的大致图像.
7.5一次函数的简单应用(2)
我预学
1. 在同一直角坐标系内作出一次函数y=-2x+3与正比例函数y=2x的图象，直线y=-x+3与直线y=2x的交点坐标是 _______，方程组 的解是___ ___.
2.阅读教材中的本节内容后回答：
例2中（1，36）点是怎么算出来的？例2(1)你能用列方程的方法来求解吗？你认为这种方法与例题中的解法有什么联系？
我求助：预习后，你或许有些疑问，请写在下面的空白处：
我梳理
两个函数图象的交点坐标即为两个函数解析式联立的 的解，反之，也可用画函数图象来解 .
个性反思：通过本节课的学习，你一定有很多感想和收获，请写在下面的空白处：
我达标
1．如图，以两条直线l1，l2的交点坐标为解的方程组是（ ）
A． B． C． D．
第1题 第2题 第3题 第4题
2．如图，OA、BA分别表示甲、乙两名学生运动的一次函数图象，图中s和t分别表示运动路程和时间，根据图象判断8秒前甲在乙的 .(填“前面”或“后面”).
3．如图，直线y=kx+b交坐标轴于A，B两点，则不等式kx+b<0的解是 .
4．如图，已知函数y=3x+b和y=ax-3的图象交于点P(-2，-5)，则根据图象可得不等式3x＋b＞ax-3的解集是_______________.
5．已知一次函数y=3x+p和y=x+q的图象都经过点A(-2，0)，且与y轴分别交于B、C两点，求△ABC的面积.
6．甲骑自行车、乙骑摩托车沿相同路线由A地到B地，行驶过程中路程与时间的函数关系的图象如图. 根据图象解决下列问题：
(1) 谁先出发？先出发多少时间？谁先到达终点？先到多少时间？
(2) 分别求出甲、乙两人的行驶速度；
(3) 在什么时间段内，两人均行驶在途中(不包括起点和终点)？在这一时间段内，请你根据下列情形，分别列出关于行驶时间x的方程或不等式(不化简，也不求解)：① 甲在乙的前面；② 甲与乙相遇；③ 甲在乙后面.
我挑战
7．无论m为何实数，直线y=x+2m与y=-x+4的交点不可能在第_______象限.
8．如图，在矩形ABCD中，AB＝4，BC＝3，点P从起点B出发，沿BC、CD逆时针方向向终点D匀速运动．设点P所走过的路程为x，则线段AP、AD与矩形的边所围成的图形的面积为y，则下列图像中能大致反映y与x函数关系的是（ ）
A． B． C． D．
9．某电视机厂要印制产品宣传材料，甲印刷厂提出：每份材料收1元印刷费，另收1000元制版费；乙厂提出：每份材料收2元印制费，不收制版费.
(1)分别写出两厂的收费y(元)与印制数量x(份)之间的函数关系式；
(2)电视机厂拟拿出3000元用于印制宣传材料，找哪家印刷厂印制的宣传材料能多一些？
(3)印刷数量在什么范围时，在甲厂的印制合算？
我登峰
10．在一条直线上依次有A、B、C三个港口，甲、乙两船同时分别从A、B港口出发，沿直线匀速驶向C港，最终达到C港．设甲、乙两船行驶x（h）后，与B港的距离分别为y1、y2（km），y1、y2与x的函数关系如图所示．
(1)填空：A、C两港口间的距离为 km， ；
(2)求图中点P的坐标，并解释该点坐标所表示的实际意义；
(3)求y1、y2与x的函数关系式；
(4)若两船的距离不超过10 km时能够相互望见，求甲、乙两船可以相互望见时x的取值范围．
7.1 常量和变量
1.S=a2；S、a 2.，h；S、a；、S；a、h 3.(1)；(2)变量：t，n；常量：120 4.是变量，因为水深h随着时间T的变化而变化 5.500米、10米/分等是常量，兔子的速度是变量 6.在0≤x≤150中，y，40是常量， x是变量；在x>150时，0.6，50是常量，x，y是变量
7.2认识函数(1)
1.；这是一个边长为10的正方形 2.3 3.12，14 4.C 5. (1)是；(2)y=2，表示弹簧的原长是2cm；(3) 原因是:弹簧所受外力超过弹性限度, 被拉长了 6.y=a(1-x)2 7.gawqj.
?7.2认识函数(2)
1.x≠-5 2. 3.y=180-2x；07.4一次函数的图象(1)
1.-5 2.(3，0)，(0，3) 3.2 4.略 5.三 6.是 7. y=-3x+6 8.射线，线段 9. 6，（7，3） 10.(1)y=2x；(2) P′(5， 2)，O′(4，0)，y=2x-8；(3) 11.(1)1小时，甲速160千米/时，乙速200千米/时；(2)S甲=t+8，S乙=2t－2；(3)P（，），乙飞机飞行了小时两机相遇
7.4一次函数的图象(2)
1.增大 2.k<0 3.<，< 4.4，-2 5.形如y=kx-k-2(k<0) 6.-57.5一次函数的简单应用(1)
1.12.5 2.B 3.100；甲；8 4.(1)(10≤x≤50)；(2)100升分 5.(1)y=1.8x+32；(2)25℃ 6.②③ 7.(1)一次函数，y=-30x＋150；(2)94升 8.(1)y=-140x＋280，280千米；(2)3.5；(3)略