第3章 实数导学案

第3章 实数
3．1 平方根
我预学
1． (1) ；
(2) ；
(3) 请写出11到20的这些数的平方的结果．
如：
2． 阅读教材中的本节内容后回答：
如果，那么谁是的平方根?
3． 阅读教材中的本节内容后回答：
本节内容中有一个平方根的重要事实“一个正数有正、负两个平方根，它们互为相反数；零的平方根是零；负数没有平方根．”
(1) 正数的平方根用什么表示？分别表示什么?
(2) 为什么负数没有平方根？
我求助：预习后，你或许有些疑问，请写在下面的空白处：
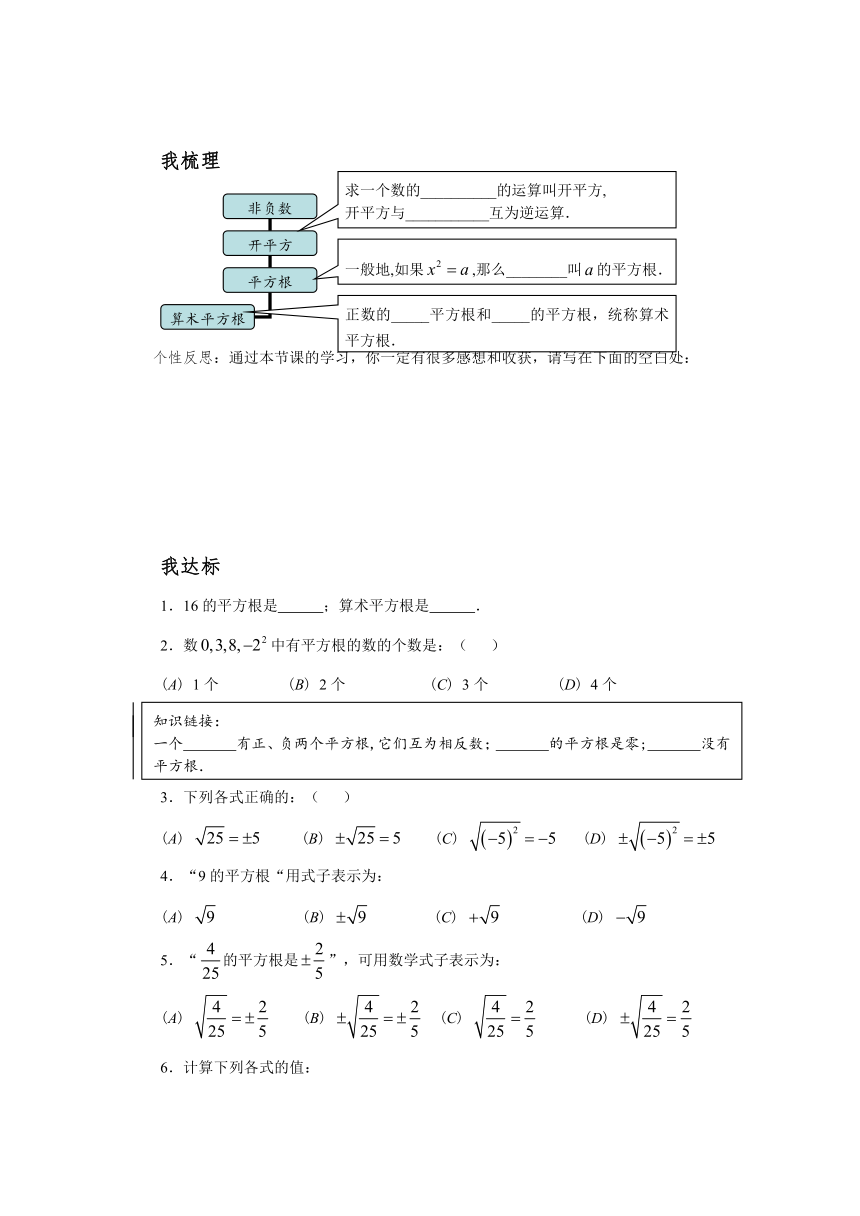
我梳理

个性反思：通过本节课的学习，你一定有很多感想和收获，请写在下面的空白处：
我达标
1．16的平方根是 ；算术平方根是 ．
2．数中有平方根的数的个数是：（ ）
(A) 1个 (B) 2个 (C) 3个 (D) 4个
3．下列各式正确的：（ ）
(A) (B) (C) (D)
4．“9的平方根“用式子表示为：
(A) (B) (C) (D)
5．“的平方根是”，可用数学式子表示为：
(A) (B) (C) (D)
6．计算下列各式的值：
(1) ； (2)； (3)； (4)；
(5)； (6)； (7)．
7．求下列各数的平方根：
(1)81； (2)0.49； (3)； (4)．
我挑战
8．算术平方根等于它本身的数有： ；平方根等于它本身的数有： ．
9． (1)是的一个平方根，则，是 的一个平方根．
(2) 的平方根是 ．
(3) 若没有平方根，则a的取值范围是 ．
10．已知一个正数a的平方根是和，求a的值．
我登峰
11．已知9和16，试写出一个数a，使这三个数中一个是另外两个数乘积的一个平方根，求出所有符合条件的数a的值．
3．2 实数
我预学
1．的算术平方根记作，那么4的算术平方根记作什么？2的算术平方根又记作什么？
2．(1)使用计算器计算，把下面两个有理数写成小数的形式：，你有什么发现？我们发现上面有理数都可以写成___________小数或____________小数的形式．
(2)什么小数叫做无理数？
3． 本节内容中有一个重要结论：“实数和数轴上的点一一对应”．阅读教材中的本节内容后填空：
如图，以一个单位长度为边画一个正方形，以原点为圆心，正方形的对角线为半径画弧，弧与数轴的交点表示两个无理数： 、 ．　　　　　　　　
上面的操作说明： 数可以用数轴上的点表示出来．也就是说数轴上的点有的表示 、有的表示 ．
我求助：预习后，你或许有些疑问，请写在下面的空白处：
我梳理
实数的两种分类：
（1）按定义分

（2）像有理数一样，无理数也有正负之分．

个性反思：通过本节课的学习，你一定有很多感想和收获，请写在下面的空白处：
我达标
1．下列实数中，无理数是（ ）
(A) (B) (C) (D)
2．两个无理数互为相反数，这两个数的商是： ．
3．写出一个比去3大且比4小的一个无理数： .
4．比较大小：
(1)； (2)
5．绝对值为的数是： ．
6．求下列各数的相反数、倒数、绝对值．
．
7． 把下列各数填入适当的括号：
分 数；
无理数；
整 数；
有理数；
我挑战
8．化简：= ．
9、在数轴上与表示的点的距离最近的整数点所表示的数是 ．
10．如图，数轴上A、B两点分别对应实数a、b，则下列结论不正确的是（　　）

(A) (B) (C) (D)
11．下列叙述正确的是（ ）
(A)有理数与无理数的和是无理数 (B)无理数与无理数的和是无理数 (C)有理数与无理数的积是无理数 (D)无理数与无理数的积是无理数．
我登峰
12．利用如图所示方格，你能画哪些边长为无理数的正方形？要求所画正方形的顶点在格点上．


3．3 立方根
我预学
1． (1) 9的平方根是多少？0的平方根是多少？负数有没有平方根？
(2) 如果一个数的平方等于a，那么这个数叫a的 ．
2．请写出1到10的这些数的立方的结果：
如：=1；
3．阅读教材中的本节内容后回答：
如果，那么谁是a的立方根?
我求助：预习后，你或许有些疑问，请写在下面的空白处：
我梳理

个性反思：通过本节课的学习，你一定有很多感想和收获，请写在下面的空白处：
我达标
1．因为 的立方是，所以的立方根是 ，即 ．
2． 的立方根与9的一个平方根的积等于 ．
3．下列各式说法不正确的是：（ ）
(A)的立方根是； (B) 的立方根是；
(C)立方根是5的数是125； (D) 64的立方根是．
4．已知立方体的体积为，则它的棱长为 cm，表面积为
5．一个正方体，体积为：它的棱长大约在：（ ）
(A) 之间 ； (B)之间 ；
(C)之间 ； (D)之间．
6．计算下列各式：
(1) ； (2) ； (3) ；
(4) ； (5) ； (6) ．
7．求下列各数的立方根：
(1)-0.064； (2)； (3)．
我挑战
8．立方根等于它本身的数有： ．平方根等于它本身的数有： ．
9． (1)的算术平方根是 ；是 的立方根．
(2)的立方根是
(3)若
10．求下式中的．

我登峰
11．(1)计算下面两组数
①
②
(2)仔细观察计算结果及被开方数之间的关系，你发现了什么?
3．4用计算器进行数的开方
我预学
我们已经学过的数的开方运算有哪些？
计算器上显示的的结果是精确值还是近似值？呢？
能利用计算器求一个数的平方根么？怎么求呢？
我求助：预习后，你或许有些疑问，请写在下面的空白处：
我达标
1．计算器按键顺序为，其显示结果为 ．
2．计算器按键顺序为，其显示结果为 ．
3．用计算器计算下列各题，并列出按键顺序：
（1） （结果保留三个有效数字）．
按键顺序为 ．
（2） （结果保留四个有效数字）．
按键顺序为 ．
4．利用计算器比较下列各对数的大小：
； ； ．
5．当球的体积为500时，球的半径=，用计算器计算该球的半径（取3.14，精确到0.01cm）
6.面积都是50平方米的圆和正方形的周长哪个大？大多少？（取3.14，精确到0.1米）
3．5实数的运算
我预学
1． (1) 我们学过哪6种运算；
(2) 其中加与减是同级运算，请说出其它二个同级运算．
2． 阅读教材中的本节内容后回答：
有理数的运算法则与运算律在实数范围内是否适用?为什么？
我求助：预习后，你或许有些疑问，请写在下面的空白处：
我梳理
实数运算的顺序：先算 ，再算 ，最后算 ，如果遇到括号，则先进行 里的运算．

个性反思：通过本节课的学习，你一定有很多感想和收获，请写在下面的空白处：
我达标
1．利用计算器验证下列计算正确的是：（ ）
(A) (B)
(C) (D)
2．按要求利用计算器计算：
（1）（精确到0．01）；
（2）（保留两个有效数字）；
（3）（精确到0.1）.
3．数轴上与表示实数的点距离为1的点所表示的数是 ．
4．要裁一块正方形的玻璃板，它的面积等于直径为7cm的圆的面积，则这一块玻璃的边长是 cm（保留两个有效数字）．
5．计算 ．
6．自由下落的物体的高度h(m)与下落的时间t(s)的关系为.有一钢球从176.4m的高空落下，它到达地面需要多少时间？
我挑战
7．实数a、b、c在数轴上对应点的位置如图，化简 ．
8．（1）计算下列式子：①；②；
③
（2）通过计算你发现了什么规律？换几个数再试试，是否有相同的规律？
第3章 实数
3.1平方根
1．±4，4 2．C 3．D 4．B 5．B 6．(1)11 (2)±16 (3)－17 (4)－(5)13 (6)－0.7 (7)± 7．(1)±9 (2)±0.7 (3)± (4)±4 8．0,1；0
9． (1)36,25 (2)±4 (3)a<4 10．49 11．±12,,
3.3立方根
1．―4,―4,－4 2．±6 3．D 4．7,294 5．A 6． (1)0.6 (2)－ (3)2
(4) 1.5 (5)－ (6)－4 7． (1) －0.4 (2) (3)－ 8．0,1,－1;0 9．(1)2,－125 (2)2 (3) 10．x=7 11．(1)略 （2）被开方数的小数点向右（或向左）移动两位，算术平方根的小数点就向右（或向左）移动一位；被开方数的小数点向右（或向左）移动三位，立方根的小数点就向右（或向左）移动一位．
3.4用计算器进行数的开方
1．1.3 2．4.25 3．(1)5.03 (2)±1.069 4．<,<,< 5．4.92
6．正方形的周长大，大3.2米.
3.5实数的运算
1．C 2． (1) (2)2.6 (3) －4.2 3．＋1,－1
4．6.2 5．1 6．6S 7． 8．(1)略 （2）两个正数的算术平方根的积等于它们的积的算术平方根．