5.2 不等式的基本性质

课件16张PPT。5.2 不等式的基本性质
1判断下列说法是否正确:
1.若a=b,b=c,则a=c
2.若a=b,则a+2=b+2
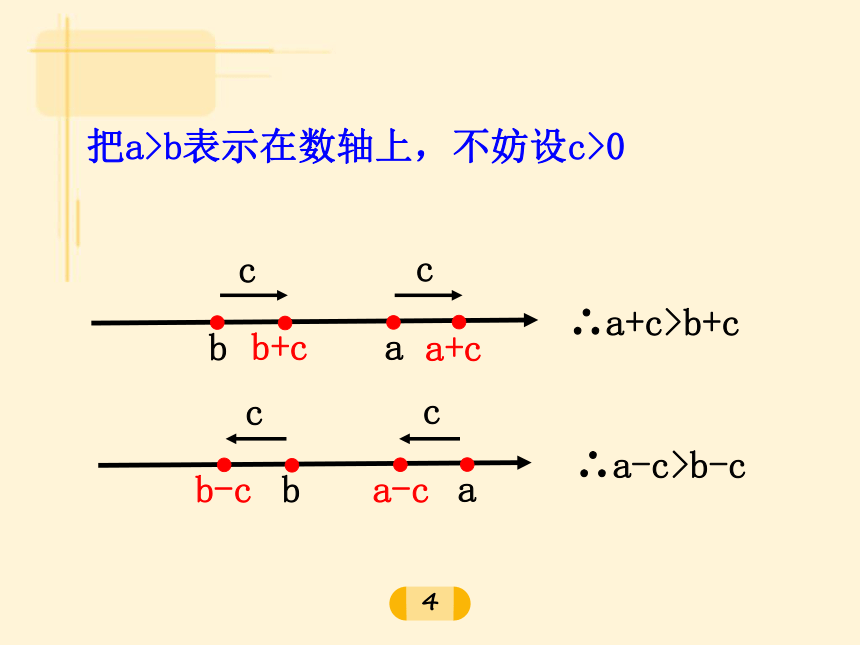
3.若a=b,则 a= b等式性质1,2,3合作学习2ab表示在数轴上，不妨设c>0∴a+c>b+c∴a-c>b-c5
不等式的两边都加上（或减去）同一个数,
所得到的不等式仍成立.
如果a＞b，那么a+c＞b+c, a-c＞b-c
如果a＜b，那么a+c＜b+c, a-c＜b-c
（不等号方向不变）1.若a>b，则b a；
2.若a>b，且b>c，则a c
3.∵0 1 ∴a a+1 ( )
4.∵(a-1)2 0,
∴ (a-1)2-2 -2 ( )练一练6选择适当的不等号填空不等式的基本性质2<<≥≥不等式的基本性质2<> -2 > -3
-2× 5 ____ -3× 5
-2×(-5) ____ -3×(-5)
-2× 0 ____ -3×0合作学习7观察并用“<”或“>”填空,并找一找其中的规律.(1) 5 > 2
5× 3 ____ 2× 3
6×(-3) ____ 2×(-3) 6× 0 ____ 2×0(2) –1 < 4
(-1)× 6 ____ 4×6
(-1)×(-6) ____ 4×(-6)
(-1)× 0 ____ 4×0>>><<<===发现：当不等式的两边
同乘同一个正数时,不等号的方向____;而乘同一个负数时,不等号的方向____。 不变改变8不等式的两边都乘(或除以)同一个正数，
所得的不等式仍成立；不等式的两边都乘(或除以)同一个负数，
必须把不等号的方向改变，所得的不等式成立.（不等号方向不变）（不等号方向改变）课内练习19(1) 若x+1＞0,两边同加上-1,得____________
(依据:_____________________);
(2) 若2 x ＞-6,两边同除以2,得____________
(依据: _______________);
(3) 若 ,两边同乘-3,得__________
(依据: _______________).x ＞-1不等式的基本性质2x＞-3不等式的基本性质3不等式的基本性质3X≥课内练习210选择恰当的不等号填空，并说出理由.(1) 若a＞-b，则a ＋ b ＿ 0.
(2) 若-a＜b，则a ＿ -b.
(3) 若-a＞-b，则2－a ＿ 2－b.
(4) 若a＞0，且（1－b）a＜0，则b ＿1.
(5) 若a＜b，b＜2a － 1，则a ＿ 2a － 1.＞＞＞＜＞例题解析例 已知a<0 ，试比较2a与a的大小.解法二：∵2＞1，a＜0
∴2a＜a（不等式的基本性质3）解法三：在数轴上分别表示2a和a的点（a＜0）
如图，2a位于a的左边，所以2a＜a 解法一：∵ a＜0
∴ a+a ＜ a (不等式的基本性质2）
即 2a ∴ 2a-a＜0
∴ 2a ∴ -3x<-3y (不等式的基本性质3)
∴ 2－3x < 2－3y (不等式的基本性质2)4.若x﹥y ，比较2－3x 与 2－3y 的大小，并说明理由. 解 ：∵x (a－3)y
∴ a－3<0 (不等式的基本性质3)
∴ a<3 (不等式的基本性质2) 5.若x (a－3)y ，求a的取值范围.变式: 若x>y，请比较(a-3)x与(a-3)y的大小 解：当a>3时，∵ x>y, a-3>0 ∴ (a-3)x>(a-3)y
当a=3时，∵ a-3=0, ∴ (a-3)x=(a-3)y=0
当a<3时，∵ x>y, a-3<0 ∴ (a-3)x<(a-3)y作业题探究活动13 比较等式与不等式的性质等式是否有与不等式的基本性质1类似的传递性？
不等式是否有与等式的基本性质类似的移项法则？
你可以用列表的方式进行对比.14 比较等式与不等式的性质说说这节课你的收获和体会
让大家与你一起分享