2021-2022学年浙教版数学九年级下2.2切线长定理 同步练习(word版含答案)
文档属性
| 名称 | 2021-2022学年浙教版数学九年级下2.2切线长定理 同步练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 311.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 20:02:15 | ||
图片预览


文档简介
2021-2022学年浙教版数学九下2.2切线长定理同步练习
一、单选题
1.如图, 为 的直径,点P在 的延长线上, 与 相切,切点分别为C,D.若 ,则 等于( )
A. B. C. D.
2.如图, 的直径AB=8,AM,BN是它的两条切线,DE与 相切于点E,并与AM,BN分别相交于D,C两点,BD,OC相交于点F,若CD=10,则BF的长是
A. B. C. D.
3.如图,从圆外一点 引圆的两条切线 , , , 为切点, 为 上的一点,连接 交 于点 ,若 , , ,则 的半径长是( )
A. B. C. D.
4.已知四边形ABCD,下列命题:①若 ,则四边形ABCD一定存在外接圆;②若四边形ABCD内存在一点到四个顶点的距离相等,则 ;③若四边形ABCD内存在一点到四条边的距离相等,则 ,其中,真命题的个数为( )
A.0 B.1 C.2 D.3
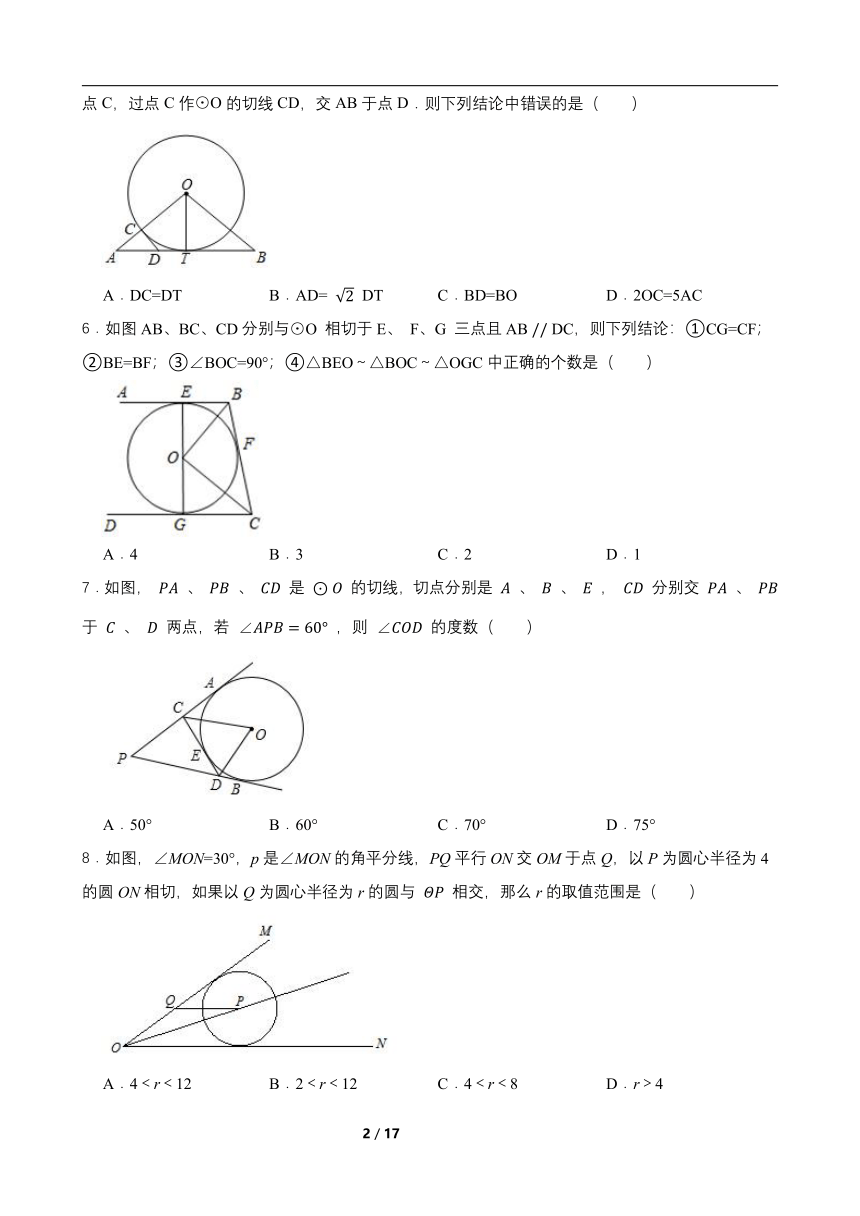
5.如图,已知OT是Rt△ABO斜边AB上的高线,AO=BO.以O为圆心,OT为半径的圆交OA于点C,过点C作⊙O的切线CD,交AB于点D.则下列结论中错误的是( )
A.DC=DT B.AD= DT C.BD=BO D.2OC=5AC
6.如图AB、BC、CD分别与⊙O 相切于E、 F、G 三点且AB DC,则下列结论:①CG=CF;②BE=BF;③∠BOC=90°;④△BEO~△BOC~△OGC中正确的个数是( )
A.4 B.3 C.2 D.1
7.如图, 、 、 是 的切线,切点分别是 、 、 , 分别交 、 于 、 两点,若 ,则 的度数( )
A.50° B.60° C.70° D.75°
8.如图,∠MON=30°,p是∠MON的角平分线,PQ平行ON交OM于点Q,以P为圆心半径为4的圆ON相切,如果以Q为圆心半径为r的圆与 相交,那么r的取值范围是( )
A.4<r<12 B.2<r<12 C.4<r<8 D.r>4
9.如图,AB是⊙O的直径,点P在BA的延长线上,PA=AO,PD与⊙O相切于点D,BC⊥AB交PD的延长线于点C,若⊙O的半径为1,则BC的长是( )
A.1.5 B.2 C. D.
10.如图,⊙O与∠α的两边相切,若∠α=60°,则图中阴影部分的面积S关于⊙O的半径r的函数图象大致是( )
A. B.
C. D.
二、填空题
11.如图,已知圆O为Rt△ABC的内切圆,切点分别为D、E、F,且∠C=90°,AB=13,BC=12,则圆O的半径为 。
12.如图,在 中, ,点 为边 上一动点,连结 .以 为圆心, 为半径作圆,交 于 ,过 作⊙O的切线,交 于点 .当⊙O与边 相切时, 的长为 .
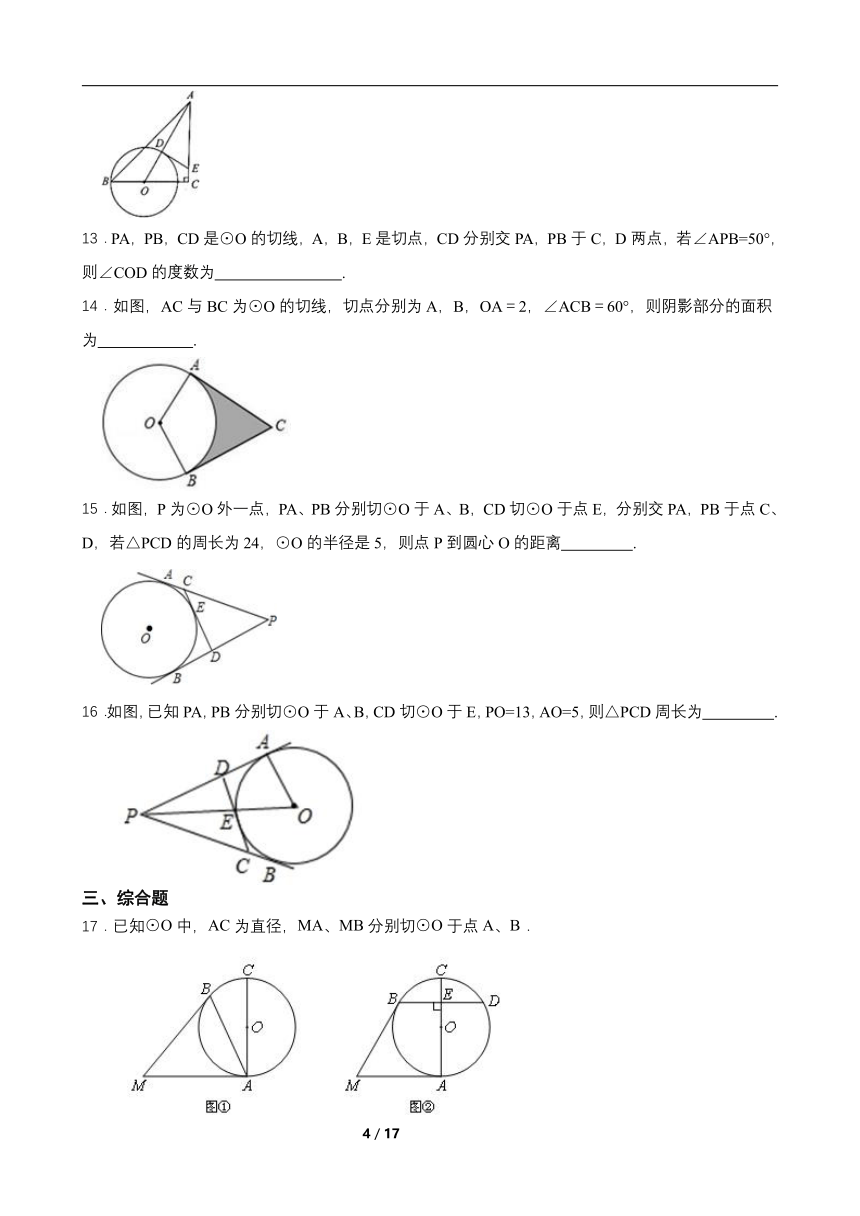
13.PA,PB,CD是⊙O的切线,A,B,E是切点,CD分别交PA,PB于C,D两点,若∠APB=50°,则∠COD的度数为 .
14.如图,AC与BC为⊙O的切线,切点分别为A,B,OA=2,∠ACB=60°,则阴影部分的面积为 .
15.如图,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA,PB于点C、D,若△PCD的周长为24,⊙O的半径是5,则点P到圆心O的距离 .
16.如图,已知PA,PB分别切⊙O于A、B,CD切⊙O于E,PO=13,AO=5,则△PCD周长为 .
三、综合题
17.已知⊙O中,AC为直径,MA、MB分别切⊙O于点A、B.
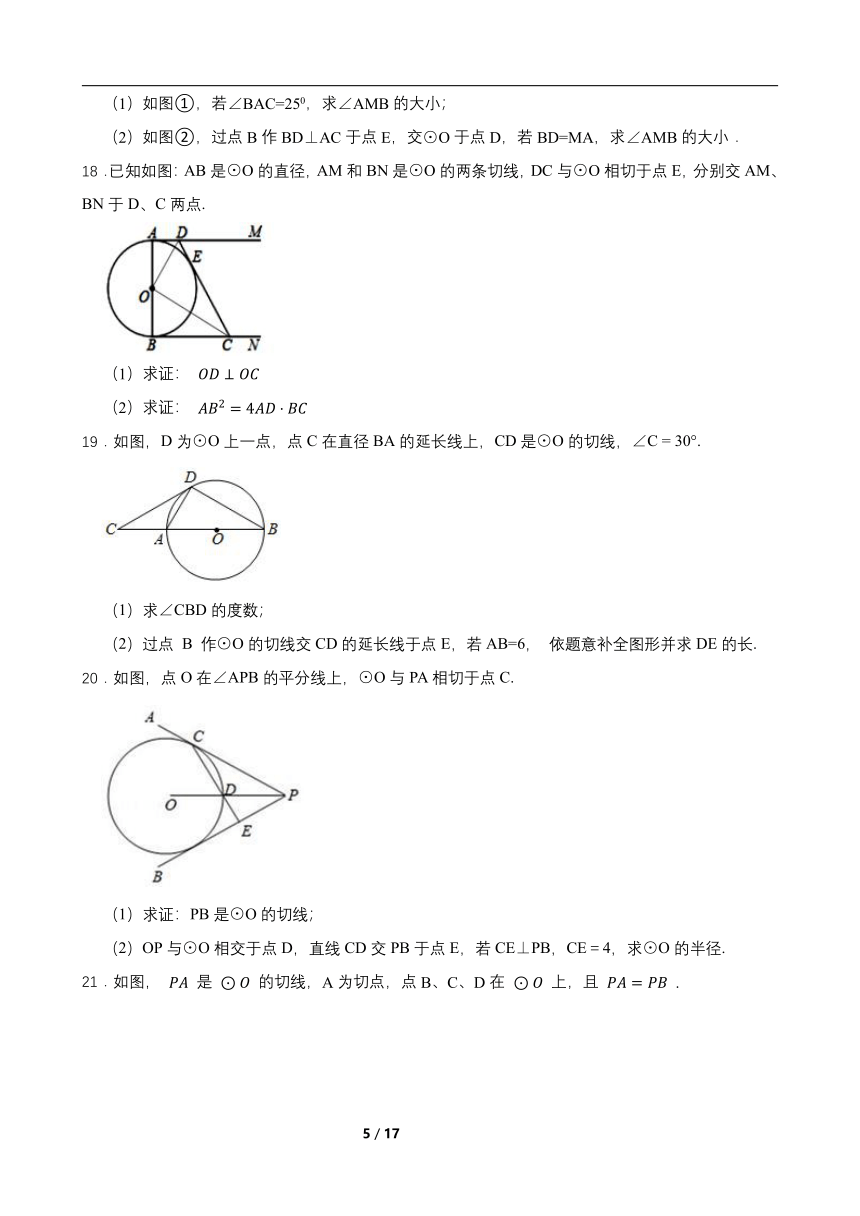
(1)如图①,若∠BAC=250,求∠AMB的大小;
(2)如图②,过点B作BD⊥AC于点E,交⊙O于点D,若BD=MA,求∠AMB的大小.
18.已知如图:AB是⊙O的直径,AM和BN是⊙O的两条切线,DC与⊙O相切于点E,分别交AM、BN于D、C两点.
(1)求证:
(2)求证:
19.如图,D为⊙O上一点,点C在直径BA的延长线上,CD是⊙O的切线,∠C = 30°.
(1)求∠CBD的度数;
(2)过点 B 作⊙O的切线交CD的延长线于点E,若AB=6, 依题意补全图形并求DE的长.
20.如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
(1)求证:PB是⊙O的切线;
(2)OP与⊙O相交于点D,直线CD交PB于点E,若CE⊥PB,CE=4,求⊙O的半径.
21.如图, 是 的切线,A为切点,点B、C、D在 上,且 .
(1)求证: 是 的切线;
(2)若 ,则 的度数为 °.
22.如图, 是 的直径, 切 于点 ,点 是 上的一点,且 , .
(1)求证: 是 的切线;
(2)若 的半径为2,求弦 及 , 的长.
23.如图,在 中, 平分 ,交 于点 ,以点 为圆心, 长为半径画 .
(1)补全图形,判断直线 与 的位置关系,并证明;
(2)若 ,求 的半径.
24.如图,射线PO与⊙O交于A、B两点,PC、PD分别与⊙O相切于点C、D.
(1)请写出两个正确结论;
(2)若PD=6,∠CPO=30°,求⊙O的半径.
25.如图, 是⊙O的切线,切点是 ,点 、 、 是 上的点, .
(1)求证: 是⊙O的切线;
(2)若 , ,则 °.
26.已知:如图, 分别切 于点 点.
(1)若 ,求 ;
(2)若 ,求 的周长.
27.如图,A是△PBD的边BD上一点,以AB为直径的 切PD于点C,过D作DE PO交PO延长线于点E,且有∠EDB=∠EPB.
(1)求证:PB是圆O的切线.
(2)若PB=6,DB=8,求 的半径.
答案
1.D
2.A
3.D
4.D
5.D
6.A
7.B
8.A
9.D
10.C
11.2
12.
13.65°或115°
14.
15.13
16.24
17.(1)解:∵MA切⊙O于点A,∴∠MAC=90°.
又∠BAC=25°,∴∠MAB=∠MAC-∠BAC=65°.
∵MA、MB分别切⊙O于点A、B,∴MA=MB.
∴∠MAB=∠MBA.
∴∠AMB=180°-(∠MAB+∠MBA)=50°.
(2)解:如图,连接AD、AB,
∵MA⊥AC,又BD⊥AC,
∴BD∥MA.
又∵BD=MA,∴四边形MADB是平行四边形.
又∵MA=MB,∴四边形MADB是菱形.∴AD=BD.
又∵AC为直径,AC⊥BD,
∴ AB =" AD" .
∴AB=AD=BD.∴△ABD是等边三角形.∴∠D=60°.
∴在菱形MADB中,∠AMB=∠D=60°
18.(1)证明:∵ 和 是它的两条切线,
∴ , ,
∴ ,
∴
∵ 切 于 ,
∴ , ,
∴ ,
∴
(2)证明:∵
∴ ,
∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
∵OA=OB
∴ ,
∴ ,
∴
19.(1)解:连接OD,如图所示:
∵CD是⊙O的切线,
∴ ,
∵∠C = 30°,
∴ ,
∵OD=OB,
∴ ,
∴
(2)解:由题意可得如图所示,
∵在Rt△ADB中, ,
∴ ,
∴ ,
∵BE、CD是圆的切线,
∴ ,
在Rt△BCD中, ,
∴ ,
∴△DEB是等边三角形,DE=DB= .
20.(1)证明:连接OC,过点O作OT⊥PB于T
∵PA是⊙O的切线,
∵OC⊥PA,
∵OP平分∠APB,OT⊥PB.
∴OC=OT,
∴PB是⊙O的切线
(2)解:∵CE⊥PB,OT⊥PB
∴∠CEP=∠OTP=90°
∴CE//OT,
∴∠ODC=∠DOT,
∵PA,PB是00的切线,
∴PC=PT,
在△OPC与△OPT 中,
∴OOPC≌OOPT(SSS),
∴∠ POC=∠POT=∠ODC
∵OC=OD
∴∠ODC=∠OCD,
∴∠COD=∠OCD=∠ODC=60°
∴△OCD是等边三角形,
∴CD=OC=OD,
∴∠OPC=90°-60°=30°
∵∠ODC=∠DCP+∠DPC,
∴∠DCP=∠DPC=30°,
∴DC=DP=OD,
∵DE//OT,
∴ET=EP,
21.(1)证明:连接 , ,
∵ 是 的切线,A为切点
∴
在 和 中,
∵ , ,
∴
∴
∴ ,且 过半径 的外端
∴ 是 的切线.
(2)220
22.(1)证明:连接OB.
∵OA=OB,
∴∠OBA=∠BAC=30°.
∴∠AOB=180°-30°-30°=120°.
∵PA切⊙O于点A,
∴OA⊥PA,
∴∠OAP=90°.
∵四边形的内角和为360°,
∴∠OBP=360°-90°-60°-120°=90°.
∴OB⊥PB.
又∵点B是⊙O上的一点,
∴PB是⊙O的切线.
(2)解:连接OP;
∵PA、PB是⊙O的切线,
∴PA=PB,∠OPA=∠OPB= ∠APB=30°.
在Rt△OAP中,∠OAP=90°,∠OPA=30°,
∴OP=2OA=2×2=4,
∴PA= = =2 .
∵PA=PB,∠APB=60°,
∴PA=PB=AB=2 .
23.(1)解:图形如图所示,结论AB与⊙D相切.
理由:过点D作DE⊥AB于E.
∵AD平分∠BAC,DC⊥AC,DE⊥AB,
∴DE=DC,
∴DE为⊙D的半径,
∴⊙D与AB相切;
(2)解:设DE=DC=r,BE=x.
∵AC⊥BC,DC为半径,
∴AC是⊙D的切线,
∵AB是⊙D的切线,
∴AC=AE=2CD=2r,
∵∠ACB=∠BED=90°,
则有 ,解得 ,
∴⊙D的半径为3.
24.(1)PC=PD,∠CPO=∠DPO
∵PC、PD分别与⊙O相切于点C、D,
∴PC=PD,∠CPO=∠DPO;
(2)连接OC,
∵PC与⊙O相切于点C,
∴OC⊥PC,
又∠CPO=30°,PC=PD=6,
∴OC=PC·tan∠CPO=6·tan30°= ,
即⊙O的半径为 .
25.(1)证明:如图,连接 , , .
∵ 是 的切线
∴
∵在 和 中, , , ,
∴ .
∴
∵点 在 上,
∴ 是 的切线
(2)76
26.(1)解:连接OA、OB和OE
∵点A和点B均为圆O的切点
∴∠PAO=∠PBO =90°
∴∠AOB=360°-∠P-∠PAO-∠PBO=140°
又CA和CE均为圆的切线
∴∠ACO=∠ECO,∠OAC=∠OEC=90°
∴∠AOC=∠EOC=
同理可得∠EOD= ∠EOB
∴∠COD=∠EOC+∠EOD= =70°
(2)解:∵PA、PB和CD分别切圆O于点A、B和E点
∴CE=CA,DE=DB,PA=PB
∴△PCD的周长=PC+PD+CD=PC+AC+PD+DB=PA+PB=2PA=20cm
27.(1)证明:∵在△DEO和△PBO中,∠EDB=∠EPB,∠DOE=∠POB,
∴∠OBP=∠E=90°,
∵OB为圆的半径
∴PB为圆O的切线;
(2)解:在R△PBD中,PB=6,DB=8,根据勾股定理得:PD= =10,
∵PD与PB都为圆的切线,
∴PC=PB=6
∴DC=PD-PC=10-6=4
在R△CDO中,设OC=T,则有
D0=8-r,
根据勾股定理得: (8-r)2=r2+42
解得:r=3,
则圆的半径为3
18 / 18
一、单选题
1.如图, 为 的直径,点P在 的延长线上, 与 相切,切点分别为C,D.若 ,则 等于( )
A. B. C. D.
2.如图, 的直径AB=8,AM,BN是它的两条切线,DE与 相切于点E,并与AM,BN分别相交于D,C两点,BD,OC相交于点F,若CD=10,则BF的长是
A. B. C. D.
3.如图,从圆外一点 引圆的两条切线 , , , 为切点, 为 上的一点,连接 交 于点 ,若 , , ,则 的半径长是( )
A. B. C. D.
4.已知四边形ABCD,下列命题:①若 ,则四边形ABCD一定存在外接圆;②若四边形ABCD内存在一点到四个顶点的距离相等,则 ;③若四边形ABCD内存在一点到四条边的距离相等,则 ,其中,真命题的个数为( )
A.0 B.1 C.2 D.3
5.如图,已知OT是Rt△ABO斜边AB上的高线,AO=BO.以O为圆心,OT为半径的圆交OA于点C,过点C作⊙O的切线CD,交AB于点D.则下列结论中错误的是( )
A.DC=DT B.AD= DT C.BD=BO D.2OC=5AC
6.如图AB、BC、CD分别与⊙O 相切于E、 F、G 三点且AB DC,则下列结论:①CG=CF;②BE=BF;③∠BOC=90°;④△BEO~△BOC~△OGC中正确的个数是( )
A.4 B.3 C.2 D.1
7.如图, 、 、 是 的切线,切点分别是 、 、 , 分别交 、 于 、 两点,若 ,则 的度数( )
A.50° B.60° C.70° D.75°
8.如图,∠MON=30°,p是∠MON的角平分线,PQ平行ON交OM于点Q,以P为圆心半径为4的圆ON相切,如果以Q为圆心半径为r的圆与 相交,那么r的取值范围是( )
A.4<r<12 B.2<r<12 C.4<r<8 D.r>4
9.如图,AB是⊙O的直径,点P在BA的延长线上,PA=AO,PD与⊙O相切于点D,BC⊥AB交PD的延长线于点C,若⊙O的半径为1,则BC的长是( )
A.1.5 B.2 C. D.
10.如图,⊙O与∠α的两边相切,若∠α=60°,则图中阴影部分的面积S关于⊙O的半径r的函数图象大致是( )
A. B.
C. D.
二、填空题
11.如图,已知圆O为Rt△ABC的内切圆,切点分别为D、E、F,且∠C=90°,AB=13,BC=12,则圆O的半径为 。
12.如图,在 中, ,点 为边 上一动点,连结 .以 为圆心, 为半径作圆,交 于 ,过 作⊙O的切线,交 于点 .当⊙O与边 相切时, 的长为 .
13.PA,PB,CD是⊙O的切线,A,B,E是切点,CD分别交PA,PB于C,D两点,若∠APB=50°,则∠COD的度数为 .
14.如图,AC与BC为⊙O的切线,切点分别为A,B,OA=2,∠ACB=60°,则阴影部分的面积为 .
15.如图,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA,PB于点C、D,若△PCD的周长为24,⊙O的半径是5,则点P到圆心O的距离 .
16.如图,已知PA,PB分别切⊙O于A、B,CD切⊙O于E,PO=13,AO=5,则△PCD周长为 .
三、综合题
17.已知⊙O中,AC为直径,MA、MB分别切⊙O于点A、B.
(1)如图①,若∠BAC=250,求∠AMB的大小;
(2)如图②,过点B作BD⊥AC于点E,交⊙O于点D,若BD=MA,求∠AMB的大小.
18.已知如图:AB是⊙O的直径,AM和BN是⊙O的两条切线,DC与⊙O相切于点E,分别交AM、BN于D、C两点.
(1)求证:
(2)求证:
19.如图,D为⊙O上一点,点C在直径BA的延长线上,CD是⊙O的切线,∠C = 30°.
(1)求∠CBD的度数;
(2)过点 B 作⊙O的切线交CD的延长线于点E,若AB=6, 依题意补全图形并求DE的长.
20.如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
(1)求证:PB是⊙O的切线;
(2)OP与⊙O相交于点D,直线CD交PB于点E,若CE⊥PB,CE=4,求⊙O的半径.
21.如图, 是 的切线,A为切点,点B、C、D在 上,且 .
(1)求证: 是 的切线;
(2)若 ,则 的度数为 °.
22.如图, 是 的直径, 切 于点 ,点 是 上的一点,且 , .
(1)求证: 是 的切线;
(2)若 的半径为2,求弦 及 , 的长.
23.如图,在 中, 平分 ,交 于点 ,以点 为圆心, 长为半径画 .
(1)补全图形,判断直线 与 的位置关系,并证明;
(2)若 ,求 的半径.
24.如图,射线PO与⊙O交于A、B两点,PC、PD分别与⊙O相切于点C、D.
(1)请写出两个正确结论;
(2)若PD=6,∠CPO=30°,求⊙O的半径.
25.如图, 是⊙O的切线,切点是 ,点 、 、 是 上的点, .
(1)求证: 是⊙O的切线;
(2)若 , ,则 °.
26.已知:如图, 分别切 于点 点.
(1)若 ,求 ;
(2)若 ,求 的周长.
27.如图,A是△PBD的边BD上一点,以AB为直径的 切PD于点C,过D作DE PO交PO延长线于点E,且有∠EDB=∠EPB.
(1)求证:PB是圆O的切线.
(2)若PB=6,DB=8,求 的半径.
答案
1.D
2.A
3.D
4.D
5.D
6.A
7.B
8.A
9.D
10.C
11.2
12.
13.65°或115°
14.
15.13
16.24
17.(1)解:∵MA切⊙O于点A,∴∠MAC=90°.
又∠BAC=25°,∴∠MAB=∠MAC-∠BAC=65°.
∵MA、MB分别切⊙O于点A、B,∴MA=MB.
∴∠MAB=∠MBA.
∴∠AMB=180°-(∠MAB+∠MBA)=50°.
(2)解:如图,连接AD、AB,
∵MA⊥AC,又BD⊥AC,
∴BD∥MA.
又∵BD=MA,∴四边形MADB是平行四边形.
又∵MA=MB,∴四边形MADB是菱形.∴AD=BD.
又∵AC为直径,AC⊥BD,
∴ AB =" AD" .
∴AB=AD=BD.∴△ABD是等边三角形.∴∠D=60°.
∴在菱形MADB中,∠AMB=∠D=60°
18.(1)证明:∵ 和 是它的两条切线,
∴ , ,
∴ ,
∴
∵ 切 于 ,
∴ , ,
∴ ,
∴
(2)证明:∵
∴ ,
∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
∵OA=OB
∴ ,
∴ ,
∴
19.(1)解:连接OD,如图所示:
∵CD是⊙O的切线,
∴ ,
∵∠C = 30°,
∴ ,
∵OD=OB,
∴ ,
∴
(2)解:由题意可得如图所示,
∵在Rt△ADB中, ,
∴ ,
∴ ,
∵BE、CD是圆的切线,
∴ ,
在Rt△BCD中, ,
∴ ,
∴△DEB是等边三角形,DE=DB= .
20.(1)证明:连接OC,过点O作OT⊥PB于T
∵PA是⊙O的切线,
∵OC⊥PA,
∵OP平分∠APB,OT⊥PB.
∴OC=OT,
∴PB是⊙O的切线
(2)解:∵CE⊥PB,OT⊥PB
∴∠CEP=∠OTP=90°
∴CE//OT,
∴∠ODC=∠DOT,
∵PA,PB是00的切线,
∴PC=PT,
在△OPC与△OPT 中,
∴OOPC≌OOPT(SSS),
∴∠ POC=∠POT=∠ODC
∵OC=OD
∴∠ODC=∠OCD,
∴∠COD=∠OCD=∠ODC=60°
∴△OCD是等边三角形,
∴CD=OC=OD,
∴∠OPC=90°-60°=30°
∵∠ODC=∠DCP+∠DPC,
∴∠DCP=∠DPC=30°,
∴DC=DP=OD,
∵DE//OT,
∴ET=EP,
21.(1)证明:连接 , ,
∵ 是 的切线,A为切点
∴
在 和 中,
∵ , ,
∴
∴
∴ ,且 过半径 的外端
∴ 是 的切线.
(2)220
22.(1)证明:连接OB.
∵OA=OB,
∴∠OBA=∠BAC=30°.
∴∠AOB=180°-30°-30°=120°.
∵PA切⊙O于点A,
∴OA⊥PA,
∴∠OAP=90°.
∵四边形的内角和为360°,
∴∠OBP=360°-90°-60°-120°=90°.
∴OB⊥PB.
又∵点B是⊙O上的一点,
∴PB是⊙O的切线.
(2)解:连接OP;
∵PA、PB是⊙O的切线,
∴PA=PB,∠OPA=∠OPB= ∠APB=30°.
在Rt△OAP中,∠OAP=90°,∠OPA=30°,
∴OP=2OA=2×2=4,
∴PA= = =2 .
∵PA=PB,∠APB=60°,
∴PA=PB=AB=2 .
23.(1)解:图形如图所示,结论AB与⊙D相切.
理由:过点D作DE⊥AB于E.
∵AD平分∠BAC,DC⊥AC,DE⊥AB,
∴DE=DC,
∴DE为⊙D的半径,
∴⊙D与AB相切;
(2)解:设DE=DC=r,BE=x.
∵AC⊥BC,DC为半径,
∴AC是⊙D的切线,
∵AB是⊙D的切线,
∴AC=AE=2CD=2r,
∵∠ACB=∠BED=90°,
则有 ,解得 ,
∴⊙D的半径为3.
24.(1)PC=PD,∠CPO=∠DPO
∵PC、PD分别与⊙O相切于点C、D,
∴PC=PD,∠CPO=∠DPO;
(2)连接OC,
∵PC与⊙O相切于点C,
∴OC⊥PC,
又∠CPO=30°,PC=PD=6,
∴OC=PC·tan∠CPO=6·tan30°= ,
即⊙O的半径为 .
25.(1)证明:如图,连接 , , .
∵ 是 的切线
∴
∵在 和 中, , , ,
∴ .
∴
∵点 在 上,
∴ 是 的切线
(2)76
26.(1)解:连接OA、OB和OE
∵点A和点B均为圆O的切点
∴∠PAO=∠PBO =90°
∴∠AOB=360°-∠P-∠PAO-∠PBO=140°
又CA和CE均为圆的切线
∴∠ACO=∠ECO,∠OAC=∠OEC=90°
∴∠AOC=∠EOC=
同理可得∠EOD= ∠EOB
∴∠COD=∠EOC+∠EOD= =70°
(2)解:∵PA、PB和CD分别切圆O于点A、B和E点
∴CE=CA,DE=DB,PA=PB
∴△PCD的周长=PC+PD+CD=PC+AC+PD+DB=PA+PB=2PA=20cm
27.(1)证明:∵在△DEO和△PBO中,∠EDB=∠EPB,∠DOE=∠POB,
∴∠OBP=∠E=90°,
∵OB为圆的半径
∴PB为圆O的切线;
(2)解:在R△PBD中,PB=6,DB=8,根据勾股定理得:PD= =10,
∵PD与PB都为圆的切线,
∴PC=PB=6
∴DC=PD-PC=10-6=4
在R△CDO中,设OC=T,则有
D0=8-r,
根据勾股定理得: (8-r)2=r2+42
解得:r=3,
则圆的半径为3
18 / 18
