2021-2022学年浙教版数学九年级下册2.3三角形的内切圆 同步练习(word版 含答案)
文档属性
| 名称 | 2021-2022学年浙教版数学九年级下册2.3三角形的内切圆 同步练习(word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 397.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-09 07:38:18 | ||
图片预览


文档简介
2021-2022学年浙教版数学九下2.3 三角形的内切圆同步练习
一、单选题
1.一直角三角形的斜边长为c,其内切圆半径是r,则三角形面积与其内切圆的面积之比是( )
A. B. C. D.
2.如图所示,已知⊙I是△ABC的内切圆,点I是内心,若∠A=35°,则∠BIC等于( )
A.35° B.70° C.145° D.107.5°
3.如图,在 中, 平分 ,使用尺规作射线 ,与 交于点 ,下列判断正确的是( )
A. 平分
B.
C.点 是 的内心
D.点 到点 , , 的距离相等
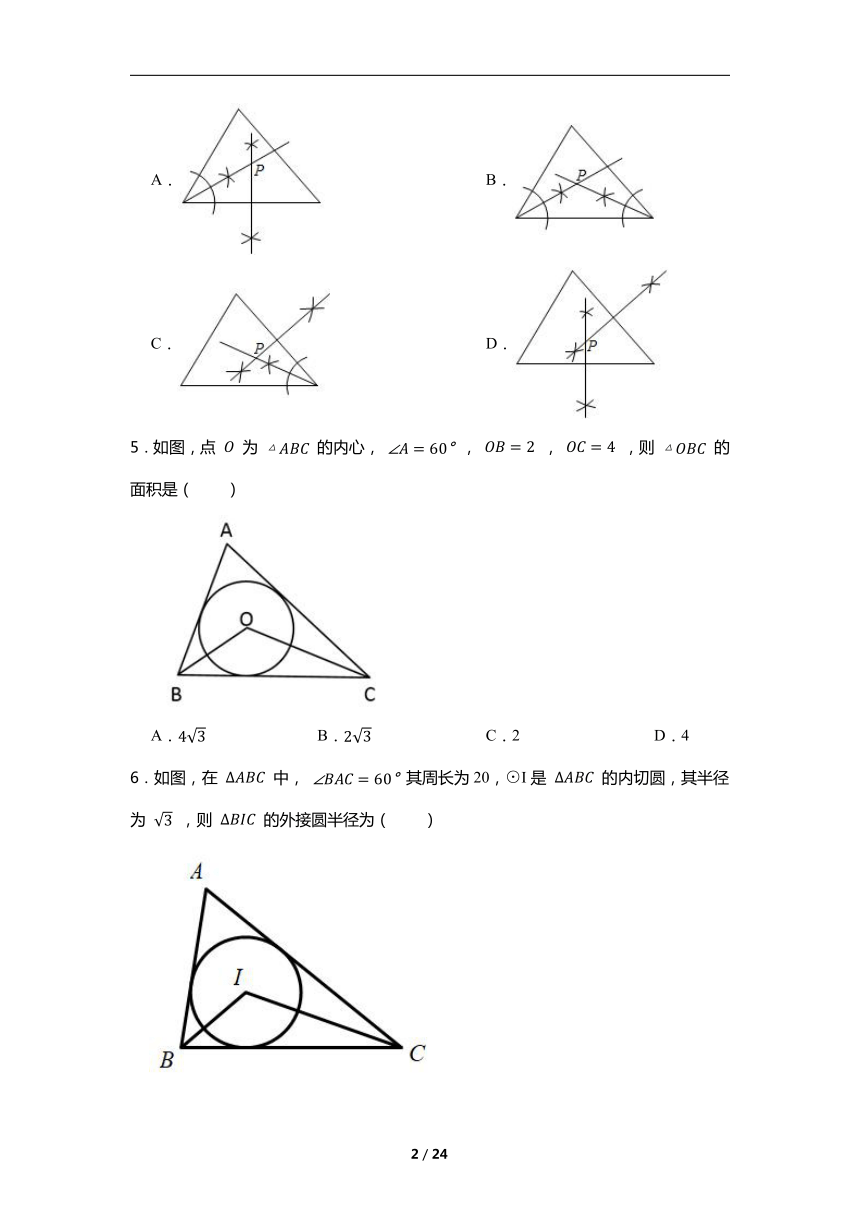
4.利用尺规作一个任意三角形的内心 ,以下作法正确的是( )
A. B.
C. D.
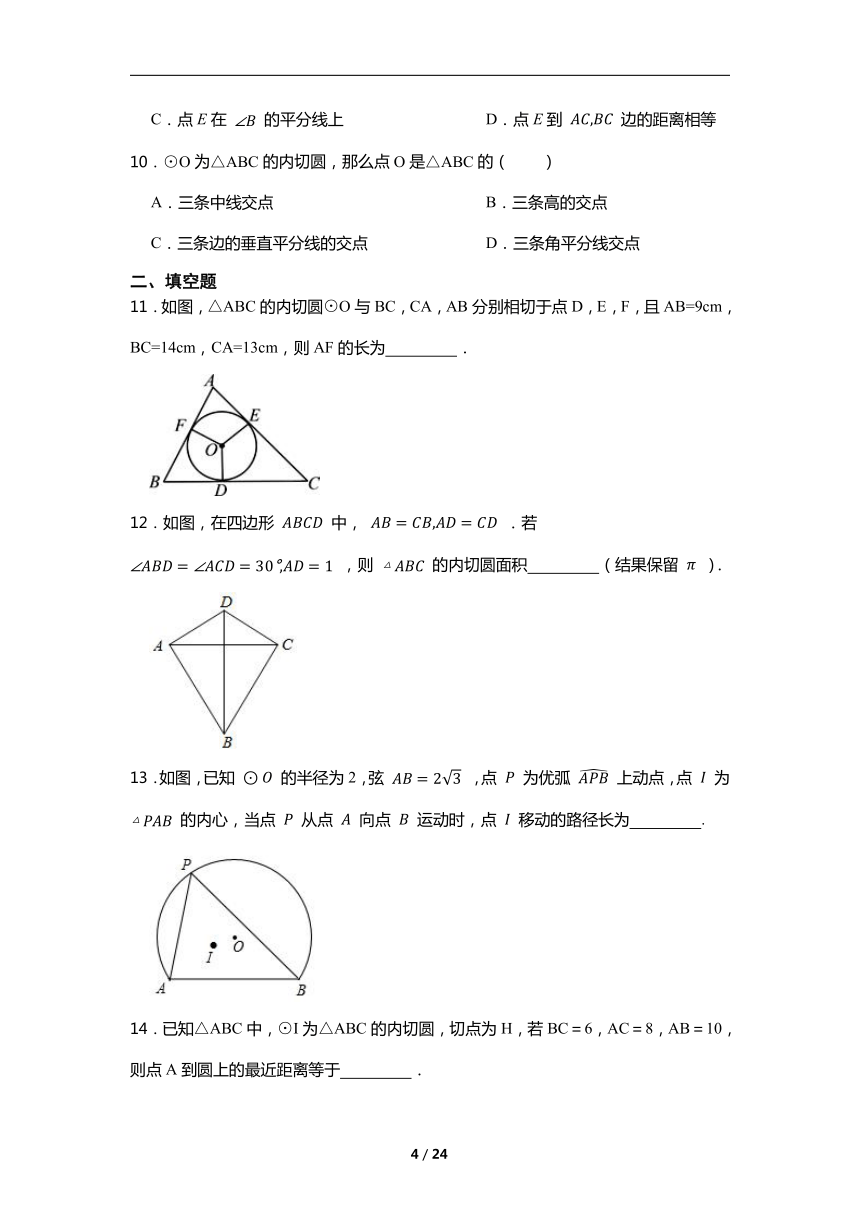
5.如图,点 为 的内心, , , ,则 的面积是( )
A. B. C.2 D.4
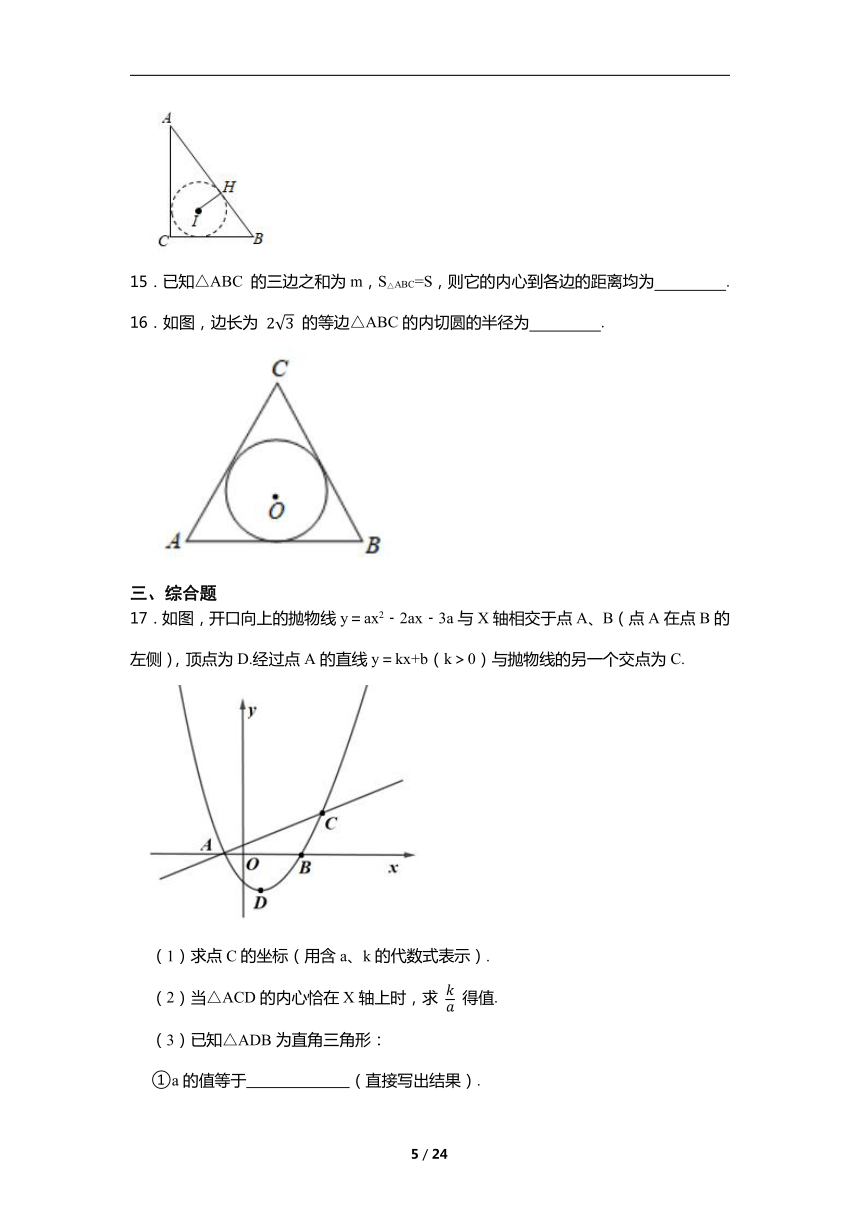
6.如图,在 中, 其周长为20,⊙I是 的内切圆,其半径为 ,则 的外接圆半径为( )
A.7 B. C. D.
7.如图所示,在4×4的网格中,A、B、C、D、O均在格点上,则点O是( )
A.△ABC的内心 B.△ABC的外心 C.△ACD的外心 D.△ACD的重心
8.如图,在 中, , 于D,⊙O为 的内切圆,设⊙O的半径为R,AD的长为h,则 的值为( )
A. B. C. D.
9.如图,在 中, .小丽按照下列方法作图:
①作 的角平分线 ,交 于点D;
②作 的垂直平分线,交 于点E.
根据小丽画出的图形,判断下列说法中正确的是( )
A.点E是 的外心 B.点E是 的内心
C.点E在 的平分线上 D.点E到 边的距离相等
10.⊙O为△ABC的内切圆,那么点O是△ABC的( )
A.三条中线交点 B.三条高的交点
C.三条边的垂直平分线的交点 D.三条角平分线交点
二、填空题
11.如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9cm,BC=14cm,CA=13cm,则AF的长为 .
12.如图,在四边形 中, .若 ,则 的内切圆面积 (结果保留 ).
13.如图,已知 的半径为2,弦 ,点 为优弧 上动点,点 为 的内心,当点 从点 向点 运动时,点 移动的路径长为 .
14.已知△ABC中,⊙I为△ABC的内切圆,切点为H,若BC=6,AC=8,AB=10,则点A到圆上的最近距离等于 .
15.已知△ABC 的三边之和为m,S△ABC=S,则它的内心到各边的距离均为 .
16.如图,边长为 的等边△ABC的内切圆的半径为 .
三、综合题
17.如图,开口向上的抛物线y=ax2﹣2ax﹣3a与X轴相交于点A、B(点A在点B的左侧),顶点为D.经过点A的直线y=kx+b(k>0)与抛物线的另一个交点为C.
(1)求点C的坐标(用含a、k的代数式表示).
(2)当△ACD的内心恰在X轴上时,求 得值.
(3)已知△ADB为直角三角形:
①a的值等于 (直接写出结果).
②若直线AC下方的拋物线上存在点P,使△APC∽△ADB,求k的值及点P的坐标.
18.如图,在由边长为1个单位长度的小正方形组成的网格中,给出了以格点(网格线的交点)为顶点的 ,且 .
(1)将 绕点 顺时针旋转90°后得到 (其中 三点旋转后的对应点分别是 ),画出 .
(2)设 的内切圆的半径为 , 的外接圆的半径为 ,则 .
19.阅读以下材料,并按要求完成相应地任务:
莱昂哈德·欧拉(Leonhard Euler)是瑞士数学家,在数学上经常见到以他的名字命名的重要常数,公式和定理,下面是欧拉发现的一个定理:在△ABC中,R和r分别为外接圆和内切圆的半径,O和I分别为其外心和内心,则 .
如图1,⊙O和⊙I分别是△ABC的外接圆和内切圆,⊙I与AB相切分于点F,设⊙O的半径为R,⊙I的半径为r,外心O(三角形三边垂直平分线的交点)与内心I(三角形三条角平分线的交点)之间的距离OI=d,则有d2=R2﹣2Rr.
下面是该定理的证明过程(部分):
延长AI交⊙O于点D,过点I作⊙O的直径MN,连接DM,AN.
∵∠D=∠N,∠DMI=∠NAI(同弧所对的圆周角相等),
∴△MDI∽△ANI,
∴ ,
∴ ①,
如图2,在图1(隐去MD,AN)的基础上作⊙O的直径DE,连接BE,BD,BI,IF,
∵DE是⊙O的直径,∴∠DBE=90°,
∵⊙I与AB相切于点F,∴∠AFI=90°,
∴∠DBE=∠IFA,
∵∠BAD=∠E(同弧所对圆周角相等),
∴△AIF∽△EDB,
∴ ,∴ ②,
任务:
(1)观察发现: , (用含R,d的代数式表示);
(2)请判断BD和ID的数量关系,并说明理由;
(3)请观察式子①和式子②,并利用任务(1),(2)的结论,按照上面的证明思路,完成该定理证明的剩余部分;
(4)应用:若△ABC的外接圆的半径为5cm,内切圆的半径为2cm,则△ABC的外心与内心之间的距离为 cm.
20.如图,点 是 的内心, 的延长线和 的外接圆 相交于点 ,过 作直线 .
(1)求证: 是 的切线;
(2)求证: ;
(3)若 , ,求 的半径.
21.有一组邻边相等且对角互补的四边形叫做等邻边互补四边形.
(1)如图1,在等邻边互补四边形ABCD中,AD=CD,且AD//BC, BC=2AD,求∠B的度数;
(2)如图2,四边形ABCD内接于圆O,连结DO交AC于点E (不与点O重合),若E是AC的中点,求证:四边形ABCD是等邻边互补四边形;
(3)在(2) 的条件下,延长DO交BC于点F,交圆0于点G,若弧BG=弧AB, tan∠ABC= ,AC=12,求FG的长;
(4)如图3,四边形ABCD内接于圆O,AB=BC, BD为圆0的直径,连结AO并延长交BC于点E,交圆0于点F,连结FC,设tan∠BAF=x, ,求y与x之间的函数关系式.
22.已知直线y= 分别交x轴、y轴于A、B两点.点P从A点出发在x轴上以每秒5个单位的速度向左运动,同时点Q从A点出发沿射线AB以每秒4个单位的速度运动.
(1)试说明:运动过程中PQ始终垂直于AB;
(2)当四边形BOPQ的面积是△ABO面积的一半时,求出发多长时间?
(3)当△APQ的内心恰好在OB上时,求运动时间.
23.在△ABC中,∠C= ,⊙O是△ABC的内切圆,⊙P分别与CA的延长线、CB的延长线以及直线AB均相切,⊙O的半径为m,⊙P的半径为n.
(1)当 =90°时,AC=6,BC=8时,m= ,n= .
(2)当 取下列度数时,求△ABC的面积(用含有m、n的代数式表示,并直接写出答案).①如图, =90°;②如图, =60°.
24.如图,在△ABC中,∠BAC=90°,∠B=60°,AB=2.AD⊥BC于D.E为边BC上的一个(不与B、C重合)点,且AE⊥EF于E,∠EAF=∠B,AF相交于点F.
(1)填空:AC= ;∠F= .
(2)当BD=DE时,证明:△ABC≌△EAF.
(3)△EAF面积的最小值是 .
(4)当△EAF的内心在△ABC的外部时,直接写出AE的范围 .
25.阅读以下材料,并按要求完成相应的任务:
莱昂哈德·欧拉(LeonhardEuler)是瑞士数学家,在数学上经常见到以他的名字命名的重要常数、公式和定理,下面是欧拉发现的一个定理:在△ABC中,R和r分别为外接圆和内切圆的半径,O和I分别为其外心和内心,则OI =R -2Rr.
下面是该定理的证明过程(借助了第(2)问的结论):
延长AI交⊙O于点D,过点I作⊙O的直径MN,连接DM,AN.
∵∠D=∠N,∴∠DMI=∠NAI(同弧所对的圆周角相等),
∴△MDI∽△ANI.∴ ,∴IA×ID=IM×IN①
如图②,在图1(隐去MD,AN)的基础上作⊙O的直径DE,连接BE,BD,BI,IF
∵DE是⊙O的直径,∴∠DBE=90°.
∵⊙I与AB相切于点F,∴∠AFI=90°,
∴∠DBE=∠IFA.
∵∠BAD=∠E(同弧所对圆周角相等),
∴△AIF∽△EDB.
∴ ,∴ ②,
由(2)知: ,
∴
又∵ ,
∴2Rr=(R+d)(R-d),
∴R -d =2Rr
∴d =R -2Rr
任务:
(1)观察发现:IM=R+d,IN= (用含R,d的代数式表示);
(2)请判断BD和ID的数量关系,并说明理由.(请利用图1证明)
(3)应用:若△ABC的外接圆的半径为6cm,内切圆的半径为2cm,则△ABC的外心与内心之间的距离 cm.
26.如图,点 是 的内心, 的延长线和 的外接圆圆 相交于点 ,过 作直线 .
(1)求证: 是圆 的切线;
(2)若 , ,求优弧 的长.
答案
1.B
2.D
3.C
4.B
5.B
6.D
7.B
8.B
9.A
10.D
11.4 cm
12.
13.
14.
15.
16.1
17.(1)解:由 , ,
解得 ,
∴ , .
∵直线 经过点A,
∴ , ,
∴直线 的解析式为 .
由 ,
解得: , ,
∴ ;
(2)解:过D作Y轴的平行线 交 于E、交X轴于点F,
∵y=ax2﹣2ax﹣3a的对称轴为 ,
∴ .
∵ 轴且点E在直线 上,
∴ .
∵ 的内心恰在x轴上,
∴x轴平分 ,
∴ ,
∴ ,
∴ ,
∴ ;
(3)①
②解:当 , 过点Р做直线 轴,作 垂足分别为M、N, ∵ , 为等腰直角三角形, ∴ 也为等腰三角形, ∴ , . , , , , ∴ , . 设 , 由 得 , 由 得 , 注意到 由上两式可解得 , , ∴ .
18.(1)解: 如图所示,
(2)
19.(1)R-d
(2)解:BD=ID,理由如下:
∵点I是△ABC的内心,
∴∠BAD=∠CAD,∠CBI=∠ABI,
∵∠DBC=∠CAD,∠BID=∠BAD+∠ABI,∠DBI=∠DBC+∠CBI,
∴∠BID=∠DBI,
∴BD=ID;
(3)解:由(2)知:BD=ID,
又 , ,
∴DE·IF=IM·IN,
∴ ,
∴
∴ ;
(4)
20.(1)证明:连接 交 于 ,如图,
∵点 是 的内心,
∴ 平分 ,即 ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ 是 的切线;
(2)连接 ,如图,
∵点 是 的内心,
∴ ,
∵ ,
∴ ,
为等腰三角形
∴ .
(3) ,
垂直平分BC
在 中
设半径为 ,则
在 中,
解得
⊙O的半径为:5.
21.(1)解:如图,作AH∥DC.
∵AD∥BC,AH∥DC,
∴四边形ABCD为平行四边形,
∴AH=CD,AD=HC.
∵AB=AD=CD,BC=2AD,
∴AB=AH=BH,
∴△ABH为等边三角形,
∴∠B=60°.
(2)证明:连接CD,如图所示:
∵ABCD为○O的内接四边形,
∴∠ABC+∠ADC=180°.
∵点E为AC的中点,
∴AE=EC,
∴OD⊥AC,
∴DA=DC,
∴四边形ABCD是等邻边互补四边形.
(3)解:如图,连接OA,OC,AG,CG,作FM⊥GC于点M,FN⊥AG于点N,
∵E为AC的中点,AC=12,
∴AE=EC=6,
∴OD⊥AC,,
∴∠AOE=∠COE,GA=GC.
∵∠AOC=2∠ABC,
∴∠AOE=∠ABC,
∴tan∠AOE=tan∠ABC==,
∴OE=,OA=,
∴CD=2OA=,DE=,
∴,
∴GA=10.
∵,
∴∠ACB=∠BCG.
∵∠AGF=∠CGF,
∴点F为△AGC的内心,
∴FM=FN=FE,设FM=FN=FE=a,则S△ACG=(AC+AG+GC)·a=·AC·EG,
∴a=3,
∴EF=3,
∴GF=EG-EF=5.
(4)解:连接AC,作AM⊥BC,FN⊥BC,设AC交BD于点K.
∵BD是直径,
∴∠BAD=∠BCD=90°.
∵BA=BC,BD=BD,
∴△ABD≌△CBD,
∴∠ABD=∠CBD.
∵OA=OB,
∴∠BAF=∠ABD=∠CBD,令∠BAF=α,则∠BCF=∠ABF=α.
∵AB=BC,∠DBA=∠DBC,
∴BD⊥AC,
∴∠ACM+∠CAM=90°,
∴∠CAM=∠CBD=α.
∵AM∥FN,
∴.
设OK=m,AK=m,OB=OA=r,则CF=2m,AC=2n.
∵m2+n2=r2,tan∠ABK=tanα=x=,
∴,
∴,
∴,
∴.
22.(1)解:把x=0代入y= 得y=0,∴点B坐标为(0,3),∴OB=3,
把y=0代入y= 得 ,解得x=4,∴点A坐标为(4,0),∴OA=4,
在Rt△OAB中,AB= .
设点P、Q运动时间为t,则AP=5t,AQ=4t
∴ ,
∵ ,
∴ ,
∵ ,
∴△APQ∽△ABO,
∴ ,
∴PQ⊥AB;
(2)解:①当P在y轴右侧时, ,
∵△APQ∽△ABO,
∴ ,
∴PA= ,
即5t= ,
∴t= ;
②当P在y轴左侧时, ,
∵△APQ∽△ABO,
∴ ,
∴PA= ,
∴5t= ,
∴t= .
综上所述,t= 或 时,四边形BOPQ的面积是△ABO面积的一半;
(3)解:如图,设△APQ的内心为I,连接AI,作IH⊥AB于H,则IH=OI=r,
∵ ,
∴ ,
∴ ,
∴AQ=4+ ,
即: ,
∴ .
23.(1)2;12
(2)解:①如图,
由(1)可知, , ,即 ,
由这两个式子可得 ;
②如图,设点D、E、F分别是3个切点,连接PD、PE、PF、CP,
由切线长定理得 ,
∵ , ,
∴ 平分 ,
∴ ,
∴ ,
∵ ,
∴ .
24.(1)2 ;30°
(2)当BD=DE时,
∵AD⊥BC于D,
∴AB=AE,
∵∠AEF=90°,∠BAC=90°,
∴∠AEF=∠BAC,
在△ABC和△EAF中, ,
∴△ABC≌△EAF(ASA);
(3)
(4) .
25.(1)
(2)解:
∵点I是△ABC的内心
∴
∵
∴
∴
(3)
26.(1)证明:连接 交 于 ,如图,
∵点 是 的内心,
∴ 平分 ,
即 ,
∴ ,
∴ , ,
∵ ,
∴ ,
∴ 是圆 的切线
(2)解:连接 、 ,如图,
∵点 是 的内心,
∴ ,
∵ ,
∴
∴ ,
∵ ,
在 中, ,
∴ ,
而 ,
∴ 为等边三角形,
∴ , ,
∴ ,
∴优弧 的长= 1 / 3
一、单选题
1.一直角三角形的斜边长为c,其内切圆半径是r,则三角形面积与其内切圆的面积之比是( )
A. B. C. D.
2.如图所示,已知⊙I是△ABC的内切圆,点I是内心,若∠A=35°,则∠BIC等于( )
A.35° B.70° C.145° D.107.5°
3.如图,在 中, 平分 ,使用尺规作射线 ,与 交于点 ,下列判断正确的是( )
A. 平分
B.
C.点 是 的内心
D.点 到点 , , 的距离相等
4.利用尺规作一个任意三角形的内心 ,以下作法正确的是( )
A. B.
C. D.
5.如图,点 为 的内心, , , ,则 的面积是( )
A. B. C.2 D.4
6.如图,在 中, 其周长为20,⊙I是 的内切圆,其半径为 ,则 的外接圆半径为( )
A.7 B. C. D.
7.如图所示,在4×4的网格中,A、B、C、D、O均在格点上,则点O是( )
A.△ABC的内心 B.△ABC的外心 C.△ACD的外心 D.△ACD的重心
8.如图,在 中, , 于D,⊙O为 的内切圆,设⊙O的半径为R,AD的长为h,则 的值为( )
A. B. C. D.
9.如图,在 中, .小丽按照下列方法作图:
①作 的角平分线 ,交 于点D;
②作 的垂直平分线,交 于点E.
根据小丽画出的图形,判断下列说法中正确的是( )
A.点E是 的外心 B.点E是 的内心
C.点E在 的平分线上 D.点E到 边的距离相等
10.⊙O为△ABC的内切圆,那么点O是△ABC的( )
A.三条中线交点 B.三条高的交点
C.三条边的垂直平分线的交点 D.三条角平分线交点
二、填空题
11.如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9cm,BC=14cm,CA=13cm,则AF的长为 .
12.如图,在四边形 中, .若 ,则 的内切圆面积 (结果保留 ).
13.如图,已知 的半径为2,弦 ,点 为优弧 上动点,点 为 的内心,当点 从点 向点 运动时,点 移动的路径长为 .
14.已知△ABC中,⊙I为△ABC的内切圆,切点为H,若BC=6,AC=8,AB=10,则点A到圆上的最近距离等于 .
15.已知△ABC 的三边之和为m,S△ABC=S,则它的内心到各边的距离均为 .
16.如图,边长为 的等边△ABC的内切圆的半径为 .
三、综合题
17.如图,开口向上的抛物线y=ax2﹣2ax﹣3a与X轴相交于点A、B(点A在点B的左侧),顶点为D.经过点A的直线y=kx+b(k>0)与抛物线的另一个交点为C.
(1)求点C的坐标(用含a、k的代数式表示).
(2)当△ACD的内心恰在X轴上时,求 得值.
(3)已知△ADB为直角三角形:
①a的值等于 (直接写出结果).
②若直线AC下方的拋物线上存在点P,使△APC∽△ADB,求k的值及点P的坐标.
18.如图,在由边长为1个单位长度的小正方形组成的网格中,给出了以格点(网格线的交点)为顶点的 ,且 .
(1)将 绕点 顺时针旋转90°后得到 (其中 三点旋转后的对应点分别是 ),画出 .
(2)设 的内切圆的半径为 , 的外接圆的半径为 ,则 .
19.阅读以下材料,并按要求完成相应地任务:
莱昂哈德·欧拉(Leonhard Euler)是瑞士数学家,在数学上经常见到以他的名字命名的重要常数,公式和定理,下面是欧拉发现的一个定理:在△ABC中,R和r分别为外接圆和内切圆的半径,O和I分别为其外心和内心,则 .
如图1,⊙O和⊙I分别是△ABC的外接圆和内切圆,⊙I与AB相切分于点F,设⊙O的半径为R,⊙I的半径为r,外心O(三角形三边垂直平分线的交点)与内心I(三角形三条角平分线的交点)之间的距离OI=d,则有d2=R2﹣2Rr.
下面是该定理的证明过程(部分):
延长AI交⊙O于点D,过点I作⊙O的直径MN,连接DM,AN.
∵∠D=∠N,∠DMI=∠NAI(同弧所对的圆周角相等),
∴△MDI∽△ANI,
∴ ,
∴ ①,
如图2,在图1(隐去MD,AN)的基础上作⊙O的直径DE,连接BE,BD,BI,IF,
∵DE是⊙O的直径,∴∠DBE=90°,
∵⊙I与AB相切于点F,∴∠AFI=90°,
∴∠DBE=∠IFA,
∵∠BAD=∠E(同弧所对圆周角相等),
∴△AIF∽△EDB,
∴ ,∴ ②,
任务:
(1)观察发现: , (用含R,d的代数式表示);
(2)请判断BD和ID的数量关系,并说明理由;
(3)请观察式子①和式子②,并利用任务(1),(2)的结论,按照上面的证明思路,完成该定理证明的剩余部分;
(4)应用:若△ABC的外接圆的半径为5cm,内切圆的半径为2cm,则△ABC的外心与内心之间的距离为 cm.
20.如图,点 是 的内心, 的延长线和 的外接圆 相交于点 ,过 作直线 .
(1)求证: 是 的切线;
(2)求证: ;
(3)若 , ,求 的半径.
21.有一组邻边相等且对角互补的四边形叫做等邻边互补四边形.
(1)如图1,在等邻边互补四边形ABCD中,AD=CD,且AD//BC, BC=2AD,求∠B的度数;
(2)如图2,四边形ABCD内接于圆O,连结DO交AC于点E (不与点O重合),若E是AC的中点,求证:四边形ABCD是等邻边互补四边形;
(3)在(2) 的条件下,延长DO交BC于点F,交圆0于点G,若弧BG=弧AB, tan∠ABC= ,AC=12,求FG的长;
(4)如图3,四边形ABCD内接于圆O,AB=BC, BD为圆0的直径,连结AO并延长交BC于点E,交圆0于点F,连结FC,设tan∠BAF=x, ,求y与x之间的函数关系式.
22.已知直线y= 分别交x轴、y轴于A、B两点.点P从A点出发在x轴上以每秒5个单位的速度向左运动,同时点Q从A点出发沿射线AB以每秒4个单位的速度运动.
(1)试说明:运动过程中PQ始终垂直于AB;
(2)当四边形BOPQ的面积是△ABO面积的一半时,求出发多长时间?
(3)当△APQ的内心恰好在OB上时,求运动时间.
23.在△ABC中,∠C= ,⊙O是△ABC的内切圆,⊙P分别与CA的延长线、CB的延长线以及直线AB均相切,⊙O的半径为m,⊙P的半径为n.
(1)当 =90°时,AC=6,BC=8时,m= ,n= .
(2)当 取下列度数时,求△ABC的面积(用含有m、n的代数式表示,并直接写出答案).①如图, =90°;②如图, =60°.
24.如图,在△ABC中,∠BAC=90°,∠B=60°,AB=2.AD⊥BC于D.E为边BC上的一个(不与B、C重合)点,且AE⊥EF于E,∠EAF=∠B,AF相交于点F.
(1)填空:AC= ;∠F= .
(2)当BD=DE时,证明:△ABC≌△EAF.
(3)△EAF面积的最小值是 .
(4)当△EAF的内心在△ABC的外部时,直接写出AE的范围 .
25.阅读以下材料,并按要求完成相应的任务:
莱昂哈德·欧拉(LeonhardEuler)是瑞士数学家,在数学上经常见到以他的名字命名的重要常数、公式和定理,下面是欧拉发现的一个定理:在△ABC中,R和r分别为外接圆和内切圆的半径,O和I分别为其外心和内心,则OI =R -2Rr.
下面是该定理的证明过程(借助了第(2)问的结论):
延长AI交⊙O于点D,过点I作⊙O的直径MN,连接DM,AN.
∵∠D=∠N,∴∠DMI=∠NAI(同弧所对的圆周角相等),
∴△MDI∽△ANI.∴ ,∴IA×ID=IM×IN①
如图②,在图1(隐去MD,AN)的基础上作⊙O的直径DE,连接BE,BD,BI,IF
∵DE是⊙O的直径,∴∠DBE=90°.
∵⊙I与AB相切于点F,∴∠AFI=90°,
∴∠DBE=∠IFA.
∵∠BAD=∠E(同弧所对圆周角相等),
∴△AIF∽△EDB.
∴ ,∴ ②,
由(2)知: ,
∴
又∵ ,
∴2Rr=(R+d)(R-d),
∴R -d =2Rr
∴d =R -2Rr
任务:
(1)观察发现:IM=R+d,IN= (用含R,d的代数式表示);
(2)请判断BD和ID的数量关系,并说明理由.(请利用图1证明)
(3)应用:若△ABC的外接圆的半径为6cm,内切圆的半径为2cm,则△ABC的外心与内心之间的距离 cm.
26.如图,点 是 的内心, 的延长线和 的外接圆圆 相交于点 ,过 作直线 .
(1)求证: 是圆 的切线;
(2)若 , ,求优弧 的长.
答案
1.B
2.D
3.C
4.B
5.B
6.D
7.B
8.B
9.A
10.D
11.4 cm
12.
13.
14.
15.
16.1
17.(1)解:由 , ,
解得 ,
∴ , .
∵直线 经过点A,
∴ , ,
∴直线 的解析式为 .
由 ,
解得: , ,
∴ ;
(2)解:过D作Y轴的平行线 交 于E、交X轴于点F,
∵y=ax2﹣2ax﹣3a的对称轴为 ,
∴ .
∵ 轴且点E在直线 上,
∴ .
∵ 的内心恰在x轴上,
∴x轴平分 ,
∴ ,
∴ ,
∴ ,
∴ ;
(3)①
②解:当 , 过点Р做直线 轴,作 垂足分别为M、N, ∵ , 为等腰直角三角形, ∴ 也为等腰三角形, ∴ , . , , , , ∴ , . 设 , 由 得 , 由 得 , 注意到 由上两式可解得 , , ∴ .
18.(1)解: 如图所示,
(2)
19.(1)R-d
(2)解:BD=ID,理由如下:
∵点I是△ABC的内心,
∴∠BAD=∠CAD,∠CBI=∠ABI,
∵∠DBC=∠CAD,∠BID=∠BAD+∠ABI,∠DBI=∠DBC+∠CBI,
∴∠BID=∠DBI,
∴BD=ID;
(3)解:由(2)知:BD=ID,
又 , ,
∴DE·IF=IM·IN,
∴ ,
∴
∴ ;
(4)
20.(1)证明:连接 交 于 ,如图,
∵点 是 的内心,
∴ 平分 ,即 ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ 是 的切线;
(2)连接 ,如图,
∵点 是 的内心,
∴ ,
∵ ,
∴ ,
为等腰三角形
∴ .
(3) ,
垂直平分BC
在 中
设半径为 ,则
在 中,
解得
⊙O的半径为:5.
21.(1)解:如图,作AH∥DC.
∵AD∥BC,AH∥DC,
∴四边形ABCD为平行四边形,
∴AH=CD,AD=HC.
∵AB=AD=CD,BC=2AD,
∴AB=AH=BH,
∴△ABH为等边三角形,
∴∠B=60°.
(2)证明:连接CD,如图所示:
∵ABCD为○O的内接四边形,
∴∠ABC+∠ADC=180°.
∵点E为AC的中点,
∴AE=EC,
∴OD⊥AC,
∴DA=DC,
∴四边形ABCD是等邻边互补四边形.
(3)解:如图,连接OA,OC,AG,CG,作FM⊥GC于点M,FN⊥AG于点N,
∵E为AC的中点,AC=12,
∴AE=EC=6,
∴OD⊥AC,,
∴∠AOE=∠COE,GA=GC.
∵∠AOC=2∠ABC,
∴∠AOE=∠ABC,
∴tan∠AOE=tan∠ABC==,
∴OE=,OA=,
∴CD=2OA=,DE=,
∴,
∴GA=10.
∵,
∴∠ACB=∠BCG.
∵∠AGF=∠CGF,
∴点F为△AGC的内心,
∴FM=FN=FE,设FM=FN=FE=a,则S△ACG=(AC+AG+GC)·a=·AC·EG,
∴a=3,
∴EF=3,
∴GF=EG-EF=5.
(4)解:连接AC,作AM⊥BC,FN⊥BC,设AC交BD于点K.
∵BD是直径,
∴∠BAD=∠BCD=90°.
∵BA=BC,BD=BD,
∴△ABD≌△CBD,
∴∠ABD=∠CBD.
∵OA=OB,
∴∠BAF=∠ABD=∠CBD,令∠BAF=α,则∠BCF=∠ABF=α.
∵AB=BC,∠DBA=∠DBC,
∴BD⊥AC,
∴∠ACM+∠CAM=90°,
∴∠CAM=∠CBD=α.
∵AM∥FN,
∴.
设OK=m,AK=m,OB=OA=r,则CF=2m,AC=2n.
∵m2+n2=r2,tan∠ABK=tanα=x=,
∴,
∴,
∴,
∴.
22.(1)解:把x=0代入y= 得y=0,∴点B坐标为(0,3),∴OB=3,
把y=0代入y= 得 ,解得x=4,∴点A坐标为(4,0),∴OA=4,
在Rt△OAB中,AB= .
设点P、Q运动时间为t,则AP=5t,AQ=4t
∴ ,
∵ ,
∴ ,
∵ ,
∴△APQ∽△ABO,
∴ ,
∴PQ⊥AB;
(2)解:①当P在y轴右侧时, ,
∵△APQ∽△ABO,
∴ ,
∴PA= ,
即5t= ,
∴t= ;
②当P在y轴左侧时, ,
∵△APQ∽△ABO,
∴ ,
∴PA= ,
∴5t= ,
∴t= .
综上所述,t= 或 时,四边形BOPQ的面积是△ABO面积的一半;
(3)解:如图,设△APQ的内心为I,连接AI,作IH⊥AB于H,则IH=OI=r,
∵ ,
∴ ,
∴ ,
∴AQ=4+ ,
即: ,
∴ .
23.(1)2;12
(2)解:①如图,
由(1)可知, , ,即 ,
由这两个式子可得 ;
②如图,设点D、E、F分别是3个切点,连接PD、PE、PF、CP,
由切线长定理得 ,
∵ , ,
∴ 平分 ,
∴ ,
∴ ,
∵ ,
∴ .
24.(1)2 ;30°
(2)当BD=DE时,
∵AD⊥BC于D,
∴AB=AE,
∵∠AEF=90°,∠BAC=90°,
∴∠AEF=∠BAC,
在△ABC和△EAF中, ,
∴△ABC≌△EAF(ASA);
(3)
(4) .
25.(1)
(2)解:
∵点I是△ABC的内心
∴
∵
∴
∴
(3)
26.(1)证明:连接 交 于 ,如图,
∵点 是 的内心,
∴ 平分 ,
即 ,
∴ ,
∴ , ,
∵ ,
∴ ,
∴ 是圆 的切线
(2)解:连接 、 ,如图,
∵点 是 的内心,
∴ ,
∵ ,
∴
∴ ,
∵ ,
在 中, ,
∴ ,
而 ,
∴ 为等边三角形,
∴ , ,
∴ ,
∴优弧 的长= 1 / 3
