5.4一元一次方程的应用(2)--等积变形问题
文档属性
| 名称 | 5.4一元一次方程的应用(2)--等积变形问题 |

|
|
| 格式 | zip | ||
| 文件大小 | 191.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-26 00:00:00 | ||
图片预览




文档简介
课件16张PPT。运用方程解决实际问题的一般过程是: 1.审题:分析题意,找出题中的数量及其关系;3.列方程:根据相等关系列出方程;4.解方程:求出未知数的值;5.检验:检查求得的值是否正确和符合实际 情形,并写出答案. 2.设元:选择一个适当的未知数用字母表示
( 例如 ) ;5.4一元一次方程的应用(二)
---等积变形问题
分析下列过程中保持不变的量
问题情境(1)“乌鸦喝水”三个石块(2)用一根15cm长的铁丝围成
一个三角形,然后把它改围成
长方形。问题情境⑶用一块橡皮泥先做成一个立
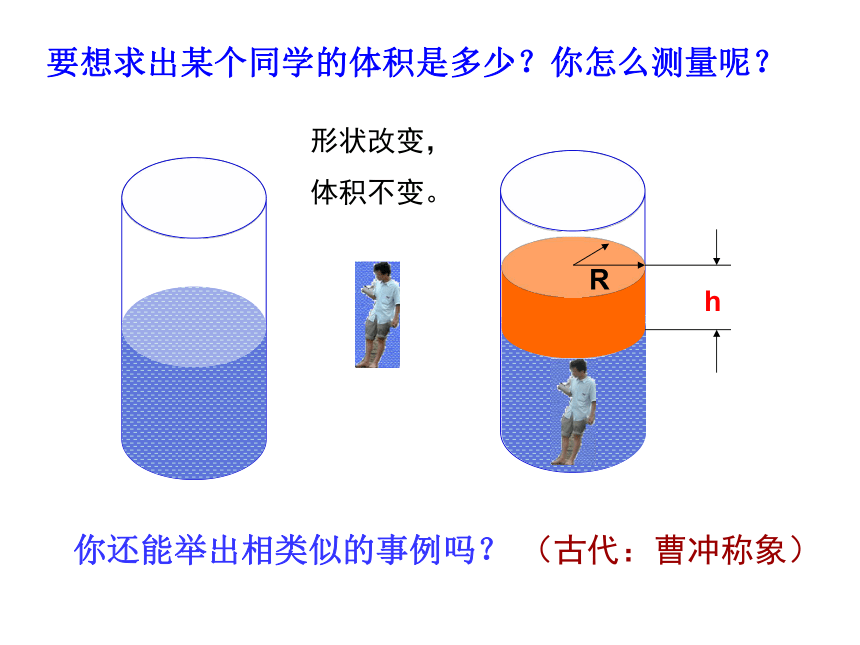
方体,再把它改做成球。问题情境hR要想求出某个同学的体积是多少?你怎么测量呢?你还能举出相类似的事例吗?(古代:曹冲称象)形状改变,
体积不变。 例题3:一标志性建筑的底面呈正方形,其四周铺上花岗石,形成一个宽为3.2米的正方形边框(如图中阴影部分),已知铺这个边框恰好用了144块边长为0.8米的正方形花岗石(接缝忽略不计),问标志性建筑底面的边长是多少米?分析:如图,若用x表示中间空白正方形的边长,本题的等量关系是什么?阴影部分的面积= 1442块边长为0.8米的正方形花岗石的面积怎样用含x的代数式表示阴影部分的面积呢? 你能设计几种不同的计算方法。方案如下:方案一方案二方案三方案四合作探究:方案二阴影部分的面积= 144块边长为0.8正方形花岗岩的面积
阴影部分的面积= 4个长为(x+3.2)米、宽为3.2米的长方形解: 设标志性建筑底面的边长为米,根据题意,得解这个方程,得x=4答:标志性建筑底面的边长为4米.
本题还有哪些解法?例题3:一标志性建筑的底面呈正方形,其四周铺上花岗岩,形成一个宽为3.2米的正方形边框(如图中阴影部分),已知铺这个边框恰好用了144块边长为0.8米的正方形花岗岩,问建筑底面的边长是多少米?4×3.2(x+3.2)=0.8×0.8×144方案二阴影部分的面积= 144块边长为0.8正方形花岗岩的面积
阴影部分的面积= 4个长为(x+3.2)米、宽为3.2米的长方形解: 设标志性建筑底面的边长为米,根据题意,得解这个方程,得x=4答:标志性建筑底面的边长为4米.
本题还有哪些解法?1、在应用方程解决问有关实际问题时,清楚地分辨量之间的关系,尤其相等关系是建立方程的关键。
2、对于等积变形问题,它的基本数量关系是相关的面积公式,相等关系的特征是存在不变量,也就是用不同的方法来计算阴影部分的面积,面积不变。4×3.2(x+3.2)=0.8×0.8×144例4.用直径为200mm的钢柱锻造一块长、宽、高分别为300mm,300mm,80mm的长方体毛坯底板,应截取圆柱多少长? (圆柱的体积=底面积×高。计算时,π取3.14,要求结果精确1mm)1.一书架能放厚为6.3cm 的书45本.现在准备放厚为 2.1cm 的书,问能放这种书多少本?练一练2.某小麦磨成面粉后质量减少15%,要得到5100千克面粉。问需要多少小麦?3.按图示的方法搭1个三角形需要3根火柴棒,搭2个三角形需要5根火柴棒.设共搭成n 个三角形,你怎样用关于是 n 的代数式表示n 个三角形需要火柴棒的根数? 现有2009根火柴棒,能搭几个这样的三角形? 2100根呢?本节课同学们学到些什么?小结:善于利用图形的面积、体积、周长及质量等
捕捉等量关系,从而列出方程。如图一个铁片长30cm,宽20cm,打算从四个角各截去一个小正方形,然后把四边折起来做一个无盖的铁盒,铁盒的底面周长为60cm,问铁盒的高是多少? 30cm20cm课后拓展如图一个铁片长30cm,宽20cm,打算从四个角各截去一个小正方形,然后把四边折起来做一个无盖的铁盒,铁盒的底面周长为60cm,问铁盒的高是多少? 30-2x20-2xx相等关系:铁盒的底面周长=60cm30-2x20-2x课后拓展
( 例如 ) ;5.4一元一次方程的应用(二)
---等积变形问题
分析下列过程中保持不变的量
问题情境(1)“乌鸦喝水”三个石块(2)用一根15cm长的铁丝围成
一个三角形,然后把它改围成
长方形。问题情境⑶用一块橡皮泥先做成一个立
方体,再把它改做成球。问题情境hR要想求出某个同学的体积是多少?你怎么测量呢?你还能举出相类似的事例吗?(古代:曹冲称象)形状改变,
体积不变。 例题3:一标志性建筑的底面呈正方形,其四周铺上花岗石,形成一个宽为3.2米的正方形边框(如图中阴影部分),已知铺这个边框恰好用了144块边长为0.8米的正方形花岗石(接缝忽略不计),问标志性建筑底面的边长是多少米?分析:如图,若用x表示中间空白正方形的边长,本题的等量关系是什么?阴影部分的面积= 1442块边长为0.8米的正方形花岗石的面积怎样用含x的代数式表示阴影部分的面积呢? 你能设计几种不同的计算方法。方案如下:方案一方案二方案三方案四合作探究:方案二阴影部分的面积= 144块边长为0.8正方形花岗岩的面积
阴影部分的面积= 4个长为(x+3.2)米、宽为3.2米的长方形解: 设标志性建筑底面的边长为米,根据题意,得解这个方程,得x=4答:标志性建筑底面的边长为4米.
本题还有哪些解法?例题3:一标志性建筑的底面呈正方形,其四周铺上花岗岩,形成一个宽为3.2米的正方形边框(如图中阴影部分),已知铺这个边框恰好用了144块边长为0.8米的正方形花岗岩,问建筑底面的边长是多少米?4×3.2(x+3.2)=0.8×0.8×144方案二阴影部分的面积= 144块边长为0.8正方形花岗岩的面积
阴影部分的面积= 4个长为(x+3.2)米、宽为3.2米的长方形解: 设标志性建筑底面的边长为米,根据题意,得解这个方程,得x=4答:标志性建筑底面的边长为4米.
本题还有哪些解法?1、在应用方程解决问有关实际问题时,清楚地分辨量之间的关系,尤其相等关系是建立方程的关键。
2、对于等积变形问题,它的基本数量关系是相关的面积公式,相等关系的特征是存在不变量,也就是用不同的方法来计算阴影部分的面积,面积不变。4×3.2(x+3.2)=0.8×0.8×144例4.用直径为200mm的钢柱锻造一块长、宽、高分别为300mm,300mm,80mm的长方体毛坯底板,应截取圆柱多少长? (圆柱的体积=底面积×高。计算时,π取3.14,要求结果精确1mm)1.一书架能放厚为6.3cm 的书45本.现在准备放厚为 2.1cm 的书,问能放这种书多少本?练一练2.某小麦磨成面粉后质量减少15%,要得到5100千克面粉。问需要多少小麦?3.按图示的方法搭1个三角形需要3根火柴棒,搭2个三角形需要5根火柴棒.设共搭成n 个三角形,你怎样用关于是 n 的代数式表示n 个三角形需要火柴棒的根数? 现有2009根火柴棒,能搭几个这样的三角形? 2100根呢?本节课同学们学到些什么?小结:善于利用图形的面积、体积、周长及质量等
捕捉等量关系,从而列出方程。如图一个铁片长30cm,宽20cm,打算从四个角各截去一个小正方形,然后把四边折起来做一个无盖的铁盒,铁盒的底面周长为60cm,问铁盒的高是多少? 30cm20cm课后拓展如图一个铁片长30cm,宽20cm,打算从四个角各截去一个小正方形,然后把四边折起来做一个无盖的铁盒,铁盒的底面周长为60cm,问铁盒的高是多少? 30-2x20-2xx相等关系:铁盒的底面周长=60cm30-2x20-2x课后拓展
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
