必修3第4章第2节 种群数量的变化
文档属性
| 名称 | 必修3第4章第2节 种群数量的变化 |  | |
| 格式 | zip | ||
| 文件大小 | 950.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 生物学 | ||
| 更新时间 | 2012-11-27 19:25:15 | ||
图片预览











文档简介
课件60张PPT。曾 石一 建构种群增长模型的方法一 建构种群增长模型的方法1. 数学模型:一 建构种群增长模型的方法1. 数学模型:是用来描述一个系统或它的性质的数学形式一 建构种群增长模型的方法1. 数学模型:是用来描述一个系统或它的性质的数学形式2. 数学模型的表现形式:一 建构种群增长模型的方法1. 数学模型:是用来描述一个系统或它的性质的数学形式2. 数学模型的表现形式:数学方程式和曲线图一 建构种群增长模型的方法1. 数学模型:是用来描述一个系统或它的性质的数学形式2. 数学模型的表现形式:数学方程式和曲线图3. 建构数学模型的意义:一 建构种群增长模型的方法1. 数学模型:是用来描述一个系统或它的性质的数学形式2. 数学模型的表现形式:数学方程式和曲线图3. 建构数学模型的意义:描述、解释和预测种群数量的变化一 建构种群增长模型的方法1. 数学模型:是用来描述一个系统或它的性质的数学形式2. 数学模型的表现形式:数学方程式和曲线图3. 建构数学模型的意义:描述、解释和预测种群数量的变化4. 数学模型建构的步骤4. 数学模型建构的步骤1 提出问题:
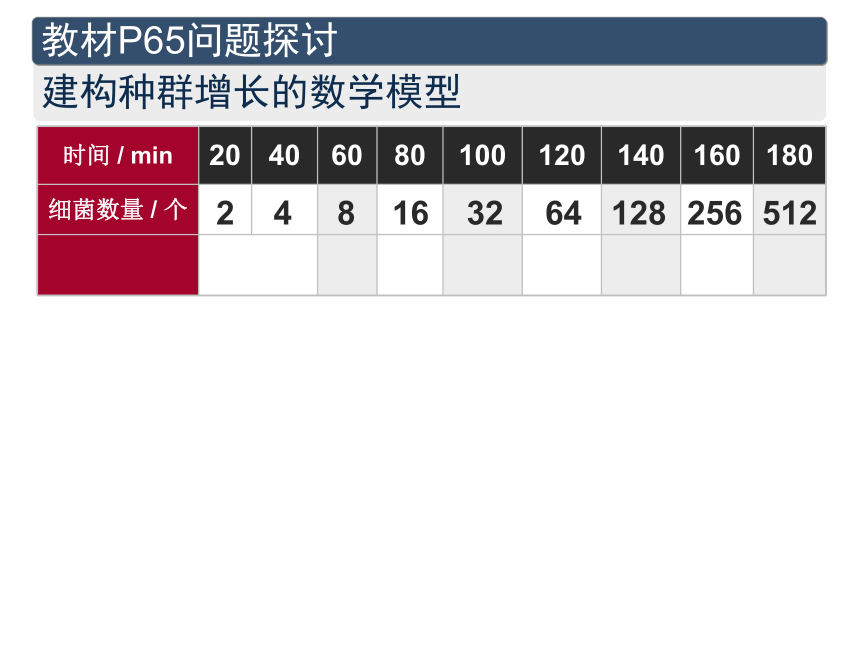
细菌的种群数量是怎样随时间变化的?2 做出假设:教材P65问题探讨建构种群增长的数学模型教材P65问题探讨建构种群增长的数学模型2481632641282565124. 数学模型建构的步骤1 提出问题:
细菌的种群数量是怎样随时间变化的?2 做出假设:
细菌的种群数量将呈指数函数形式进行增长。3 构建数学模型:
方程式: Nt = N0×λt4. 数学模型建构的步骤1 提出问题:
细菌的种群数量是怎样随时间变化的?2 做出假设:
细菌的种群数量将呈指数函数形式进行增长。3 构建数学模型:
方程式: Nt = N0×λt
曲线图:t(时间)为横坐标,Nt(种群数量)为纵坐标教材P65问题探讨建构种群增长的数学模型24816326412825651260050040030020010020406080100180时间4. 数学模型建构的步骤1 提出问题:
细菌的种群数量是怎样随时间变化的?2 做出假设:
细菌的种群数量将呈指数函数形式进行增长。3 构建数学模型:
方程式: Nt = N0×λt
曲线图:t(时间)为横坐标,Nt(种群数量)为纵坐标4 实验验证:4. 数学模型建构的步骤1 提出问题:
细菌的种群数量是怎样随时间变化的?2 做出假设:
细菌的种群数量将呈指数函数形式进行增长。3 构建数学模型:
方程式: Nt = N0×λt
曲线图:t(时间)为横坐标,Nt(种群数量)为纵坐标4 实验验证:
根据实验所获得的相关数据,对模型进行检验或修正。那么自然界中的种群数量变化情况是怎么样的呢?一 建构种群增长模型的方法二 种群增长的“J”型曲线实例1澳大利亚本来并没有兔子。 1859年,24只欧
洲野兔从英国被带到了澳大利亚。这些野兔发
现自己来到了天堂。因为这里有茂盛的牧草,
却没有鹰等天敌。这里的土壤疏松,打洞做窝
非常方便。于是,兔子开始了几乎不受任何限
制的大量繁殖。不到100年,兔子的数量达到
6 亿只以上,遍布整个大陆。凤眼莲(水葫芦)二 种群增长的“J”型曲线实例320世纪30年代,人们将环颈雉引入美国华盛顿
州的一个海岛。1937—1942年间数量增长:二 种群增长的“J”型曲线①产生条件: 二 种群增长的“J”型曲线①产生条件: ②增长特点: (实验室环境或者外来物种入侵时)
食物充足,空间不限,气候适宜,没有敌害等;
种群数量越来越多;
增长速率越来越快;
增长率保持不变。二 种群增长的“J”型曲线①产生条件: ②增长特点: ③量的计算:t年后种群的数量为:Nt=N0λt N0为起始数量, t为时间,Nt表示t年后该种群
的数量,λ为年均增长率。种群数量越来越多;
增长速率越来越快;
增长率保持不变。在有限的资源环境下,种群的数量增长又会呈现为什么样的发展规律呢?二 种群增长的“J”型曲线三 种群增长的“S”型曲线高斯实验:生态学家曾经做过这样的实验:在0.5mL
培养液中放入5个大草履虫,然后每隔24h统计一次大
草履虫数量。经过反复实验,得出了如上图所示结果。
从上图可以看出,大草履虫在这个实验环境条件下的
最大种群数量是375个,这就是该实验种群的K值。二 种群增长的“J”型曲线三 种群增长的“S”型曲线种群经过一定时间的增长后,数量趋于
稳定的增长曲线称为“S”型曲线。三 种群增长的“S”型曲线12345670100200300400K值:环境容纳量时间/天酵
母
数三 种群增长的“S”型曲线12345670100200300400K值:环境容纳量时间/天酵
母
数三 种群增长的“S”型曲线12345670100200300400K值:环境容纳量时间/天酵
母
数三 种群增长的“S”型曲线12345670100200300400K值:环境容纳量环境阻力时间/天酵
母
数三 种群增长的“S”型曲线12345670100200300400K值:环境容纳量环境阻力时间/天酵
母
数食物不足
空间有限
种内斗争
天敌捕食
气候不适
寄生虫
传染病等三 种群增长的“S”型曲线1.产生条件:存在环境阻力:2.增长特点:自然条件(现实状态):食物等资源和空间
是有限的,存在有天敌。种
群
数
量
“S”
型
增
长
曲
线K种
群
数
量
“S”
型
增
长
曲
线(种群数量)KD: 出生率=死亡率,即
种群数量处于K值。种
群
数
量
“S”
型
增
长
曲
线(种群数量)K种
群
数
量
增
长
率时间D: 出生率=死亡率,即
种群数量处于K值。种
群
数
量
“S”
型
增
长
曲
线(种群数量)K时间D: 出生率=死亡率,即
种群数量处于K值。种
群
数
量
增
长
率种
群
数
量
“S”
型
增
长
曲
线(种群数量)K时间D: 出生率=死亡率,即
种群数量处于K值。种
群
数
量
增
长
率种
群
数
量
“S”
型
增
长
曲
线(种群数量)K/2K时间D: 出生率=死亡率,即
种群数量处于K值。种
群
数
量
增
长
率种
群
数
量
“S”
型
增
长
曲
线(种群数量)K/2K种
群
数
量
增
长
率时间D: 出生率=死亡率,即
种群数量处于K值。B: 出生率与死亡率之差
最大,即种群数量处于
K/2值。三 种群增长的“S”型曲线1.产生条件:存在环境阻力:2.增长特点:①种群数量的增长存在有环境所允许的最大值
(K值)。②种群增长速率和增长率都是先越来越快,在
k/2左右达到最大值,然后越来越慢,到达K值
时变为0.自然条件(现实状态):食物等资源和空间
是有限的,存在有天敌。③越靠近K值,环境阻力越大,生存斗争越剧烈。三 种群增长的“S”型曲线3.种群数量增长到K值后不再继续增加的原因:内因是: 种群出生率+迁入率=死亡率+迁出率外因是: 自然界的资源和空间是有限的,存在天敌种群增长的 “J”型曲线种群增长的 “S”型曲线
种群增长的 “J”型曲线种群增长的 “S”型曲线三、种群增长的“S”型曲线问题:种群数量达到K值时,都能在K值维持稳定吗?三、种群增长的“S”型曲线问题:种群数量达到K值时,都能在K值维持稳定吗?环境条件的改变,K值也随之发生改变,即改
善环境条件可使K值增大,如环境条件受到破
坏,则K值将会减小。 2.下图表示接种到一定容积培养液中的酵母菌生长曲线图,曲线中哪段表示由于有限空间资源的限制使种内竞争最为剧烈( ) A.CD段
B.DE段
C.EF段
D.FG段例( 05全国卷II) 为了保护鱼类资源不受破坏,并能持
续地获得最大捕鱼量,根据种群增长的S型曲线,应使
被捕鱼群的种群数量保持在 K/2水平。这是因为在这个
水平上
A. 种群数量相对稳定
B. 种群增长量最大
C. 种群数量最大
D. 环境条件所允许的种群数量最大例( 05全国卷II) 为了保护鱼类资源不受破坏,并能持
续地获得最大捕鱼量,根据种群增长的S型曲线,应使
被捕鱼群的种群数量保持在 K/2水平。这是因为在这个
水平上
A. 种群数量相对稳定
B. 种群增长量最大
C. 种群数量最大
D. 环境条件所允许的种群数量最大K时间K/2种群数量3 在一个玻璃容器内,装入一定量的符合小球藻生活的营养液,接种少量的小球藻,每隔一段时间测定小球藻的个体数量,绘制成曲线,如右图所示。下列四图中能正确表示小球藻种群数量增长率随时间变化趋势的曲线是在现实的生态系统中,种群数量除增长外,还
有没有其他变化?时间总
数
量增长种群数量在时间过程中的动态
(仿Clarke,1954)在现实的生态系统中,种群数量除增长外,还
有没有其他变化?时间总
数
量增长周期性波动不规则波动平衡水平衰落灭亡种群数量在时间过程中的动态
(仿Clarke,1954)培养液中酵母菌种群数量的变化探究:探究过程1.提出问题:
2.作出假设:
3.设计实验:
4.进行实验:
5.分析结果和
表达交流:
6.得出结论:培养液中酵母菌种群的数量是怎样随时间变化的?酵母菌在开始一段时间呈“J”型增长,随着时间的推移,由于资源和空间有限,呈“S”型增长。 连续培养5天,每天用显微镜和血球计数板计数出酵母菌种群密度各小组汇报实验结果,结合前4天的结果,画出酵母种群增长的曲线图并进行分析。 酵母菌在开始一段时间呈“J”型增长,但随着时间的推移,由于资源和空间有限,将呈“S”型增长,并最终将全部死亡。 计数室如何计数?五点取样法样方法A1A2A5A3A4酵母菌数量变化记录表计数时有哪些注意事项?①从试管中吸出培养液进行计数之前,要将试管轻轻震荡几次;
如果酵母菌浓度过大,应先稀释。②对于压在中格界线上的酵母菌,一般只取相邻两边及夹角计数;③对于已经出芽的酵母菌,芽体达到母细胞大小一半时,即可作为两个菌体计算;已死亡的酵母菌不计数※。④每个样品一般计数三次,取其平均值。
细菌的种群数量是怎样随时间变化的?2 做出假设:教材P65问题探讨建构种群增长的数学模型教材P65问题探讨建构种群增长的数学模型2481632641282565124. 数学模型建构的步骤1 提出问题:
细菌的种群数量是怎样随时间变化的?2 做出假设:
细菌的种群数量将呈指数函数形式进行增长。3 构建数学模型:
方程式: Nt = N0×λt4. 数学模型建构的步骤1 提出问题:
细菌的种群数量是怎样随时间变化的?2 做出假设:
细菌的种群数量将呈指数函数形式进行增长。3 构建数学模型:
方程式: Nt = N0×λt
曲线图:t(时间)为横坐标,Nt(种群数量)为纵坐标教材P65问题探讨建构种群增长的数学模型24816326412825651260050040030020010020406080100180时间4. 数学模型建构的步骤1 提出问题:
细菌的种群数量是怎样随时间变化的?2 做出假设:
细菌的种群数量将呈指数函数形式进行增长。3 构建数学模型:
方程式: Nt = N0×λt
曲线图:t(时间)为横坐标,Nt(种群数量)为纵坐标4 实验验证:4. 数学模型建构的步骤1 提出问题:
细菌的种群数量是怎样随时间变化的?2 做出假设:
细菌的种群数量将呈指数函数形式进行增长。3 构建数学模型:
方程式: Nt = N0×λt
曲线图:t(时间)为横坐标,Nt(种群数量)为纵坐标4 实验验证:
根据实验所获得的相关数据,对模型进行检验或修正。那么自然界中的种群数量变化情况是怎么样的呢?一 建构种群增长模型的方法二 种群增长的“J”型曲线实例1澳大利亚本来并没有兔子。 1859年,24只欧
洲野兔从英国被带到了澳大利亚。这些野兔发
现自己来到了天堂。因为这里有茂盛的牧草,
却没有鹰等天敌。这里的土壤疏松,打洞做窝
非常方便。于是,兔子开始了几乎不受任何限
制的大量繁殖。不到100年,兔子的数量达到
6 亿只以上,遍布整个大陆。凤眼莲(水葫芦)二 种群增长的“J”型曲线实例320世纪30年代,人们将环颈雉引入美国华盛顿
州的一个海岛。1937—1942年间数量增长:二 种群增长的“J”型曲线①产生条件: 二 种群增长的“J”型曲线①产生条件: ②增长特点: (实验室环境或者外来物种入侵时)
食物充足,空间不限,气候适宜,没有敌害等;
种群数量越来越多;
增长速率越来越快;
增长率保持不变。二 种群增长的“J”型曲线①产生条件: ②增长特点: ③量的计算:t年后种群的数量为:Nt=N0λt N0为起始数量, t为时间,Nt表示t年后该种群
的数量,λ为年均增长率。种群数量越来越多;
增长速率越来越快;
增长率保持不变。在有限的资源环境下,种群的数量增长又会呈现为什么样的发展规律呢?二 种群增长的“J”型曲线三 种群增长的“S”型曲线高斯实验:生态学家曾经做过这样的实验:在0.5mL
培养液中放入5个大草履虫,然后每隔24h统计一次大
草履虫数量。经过反复实验,得出了如上图所示结果。
从上图可以看出,大草履虫在这个实验环境条件下的
最大种群数量是375个,这就是该实验种群的K值。二 种群增长的“J”型曲线三 种群增长的“S”型曲线种群经过一定时间的增长后,数量趋于
稳定的增长曲线称为“S”型曲线。三 种群增长的“S”型曲线12345670100200300400K值:环境容纳量时间/天酵
母
数三 种群增长的“S”型曲线12345670100200300400K值:环境容纳量时间/天酵
母
数三 种群增长的“S”型曲线12345670100200300400K值:环境容纳量时间/天酵
母
数三 种群增长的“S”型曲线12345670100200300400K值:环境容纳量环境阻力时间/天酵
母
数三 种群增长的“S”型曲线12345670100200300400K值:环境容纳量环境阻力时间/天酵
母
数食物不足
空间有限
种内斗争
天敌捕食
气候不适
寄生虫
传染病等三 种群增长的“S”型曲线1.产生条件:存在环境阻力:2.增长特点:自然条件(现实状态):食物等资源和空间
是有限的,存在有天敌。种
群
数
量
“S”
型
增
长
曲
线K种
群
数
量
“S”
型
增
长
曲
线(种群数量)KD: 出生率=死亡率,即
种群数量处于K值。种
群
数
量
“S”
型
增
长
曲
线(种群数量)K种
群
数
量
增
长
率时间D: 出生率=死亡率,即
种群数量处于K值。种
群
数
量
“S”
型
增
长
曲
线(种群数量)K时间D: 出生率=死亡率,即
种群数量处于K值。种
群
数
量
增
长
率种
群
数
量
“S”
型
增
长
曲
线(种群数量)K时间D: 出生率=死亡率,即
种群数量处于K值。种
群
数
量
增
长
率种
群
数
量
“S”
型
增
长
曲
线(种群数量)K/2K时间D: 出生率=死亡率,即
种群数量处于K值。种
群
数
量
增
长
率种
群
数
量
“S”
型
增
长
曲
线(种群数量)K/2K种
群
数
量
增
长
率时间D: 出生率=死亡率,即
种群数量处于K值。B: 出生率与死亡率之差
最大,即种群数量处于
K/2值。三 种群增长的“S”型曲线1.产生条件:存在环境阻力:2.增长特点:①种群数量的增长存在有环境所允许的最大值
(K值)。②种群增长速率和增长率都是先越来越快,在
k/2左右达到最大值,然后越来越慢,到达K值
时变为0.自然条件(现实状态):食物等资源和空间
是有限的,存在有天敌。③越靠近K值,环境阻力越大,生存斗争越剧烈。三 种群增长的“S”型曲线3.种群数量增长到K值后不再继续增加的原因:内因是: 种群出生率+迁入率=死亡率+迁出率外因是: 自然界的资源和空间是有限的,存在天敌种群增长的 “J”型曲线种群增长的 “S”型曲线
种群增长的 “J”型曲线种群增长的 “S”型曲线三、种群增长的“S”型曲线问题:种群数量达到K值时,都能在K值维持稳定吗?三、种群增长的“S”型曲线问题:种群数量达到K值时,都能在K值维持稳定吗?环境条件的改变,K值也随之发生改变,即改
善环境条件可使K值增大,如环境条件受到破
坏,则K值将会减小。 2.下图表示接种到一定容积培养液中的酵母菌生长曲线图,曲线中哪段表示由于有限空间资源的限制使种内竞争最为剧烈( ) A.CD段
B.DE段
C.EF段
D.FG段例( 05全国卷II) 为了保护鱼类资源不受破坏,并能持
续地获得最大捕鱼量,根据种群增长的S型曲线,应使
被捕鱼群的种群数量保持在 K/2水平。这是因为在这个
水平上
A. 种群数量相对稳定
B. 种群增长量最大
C. 种群数量最大
D. 环境条件所允许的种群数量最大例( 05全国卷II) 为了保护鱼类资源不受破坏,并能持
续地获得最大捕鱼量,根据种群增长的S型曲线,应使
被捕鱼群的种群数量保持在 K/2水平。这是因为在这个
水平上
A. 种群数量相对稳定
B. 种群增长量最大
C. 种群数量最大
D. 环境条件所允许的种群数量最大K时间K/2种群数量3 在一个玻璃容器内,装入一定量的符合小球藻生活的营养液,接种少量的小球藻,每隔一段时间测定小球藻的个体数量,绘制成曲线,如右图所示。下列四图中能正确表示小球藻种群数量增长率随时间变化趋势的曲线是在现实的生态系统中,种群数量除增长外,还
有没有其他变化?时间总
数
量增长种群数量在时间过程中的动态
(仿Clarke,1954)在现实的生态系统中,种群数量除增长外,还
有没有其他变化?时间总
数
量增长周期性波动不规则波动平衡水平衰落灭亡种群数量在时间过程中的动态
(仿Clarke,1954)培养液中酵母菌种群数量的变化探究:探究过程1.提出问题:
2.作出假设:
3.设计实验:
4.进行实验:
5.分析结果和
表达交流:
6.得出结论:培养液中酵母菌种群的数量是怎样随时间变化的?酵母菌在开始一段时间呈“J”型增长,随着时间的推移,由于资源和空间有限,呈“S”型增长。 连续培养5天,每天用显微镜和血球计数板计数出酵母菌种群密度各小组汇报实验结果,结合前4天的结果,画出酵母种群增长的曲线图并进行分析。 酵母菌在开始一段时间呈“J”型增长,但随着时间的推移,由于资源和空间有限,将呈“S”型增长,并最终将全部死亡。 计数室如何计数?五点取样法样方法A1A2A5A3A4酵母菌数量变化记录表计数时有哪些注意事项?①从试管中吸出培养液进行计数之前,要将试管轻轻震荡几次;
如果酵母菌浓度过大,应先稀释。②对于压在中格界线上的酵母菌,一般只取相邻两边及夹角计数;③对于已经出芽的酵母菌,芽体达到母细胞大小一半时,即可作为两个菌体计算;已死亡的酵母菌不计数※。④每个样品一般计数三次,取其平均值。
同课章节目录
- 第1章 人体的内环境与稳态
- 第1节 细胞生活的环境
- 第2节 内环境稳态的重要性
- 第2章 动物和人体生命活动的调节
- 第1节 通过神经系统的调节
- 第2节 通过激素的调节
- 第3节 神经调节与体液调节的关系
- 第4节 免疫调节
- 第3章 植物的激素调节
- 第1节 植物生长素的发现
- 第2节 生长素的生理作用
- 第3节 其他植物激素
- 第4章 种群和群落
- 第1节 种群的特征
- 第2节 种群数量的变化
- 第3节 群落的结构
- 第4节 群落的演替
- 第5章 生态系统及其稳定性
- 第1节 生态系统的结构
- 第2节 生态系统的能量流动
- 第3节 生态系统的物质循环
- 第4节 生态系统的信息传递
- 第5节 生态系统的稳定性
- 第6章 生态环境的保护
- 第1节 人口增长对生态环境的影响
- 第2节 保护我们共同的家园
