5.4一元一次方程的应用(2)---等积变形
文档属性
| 名称 | 5.4一元一次方程的应用(2)---等积变形 |  | |
| 格式 | zip | ||
| 文件大小 | 328.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-03 16:35:57 | ||
图片预览








文档简介
课件23张PPT。运用方程解决实际问题的一般过程是: 1.审题: 3.列方程: 4.解方程:5.检验: 2.设元:分析题意,找出题中的数量及其关系; 选择一个适当的未知数用字母表示
( 例如 ) ;其它的量用含x的代数式表示出来根据相等关系列出方程;求出未知数的值;
检查求得的值是否正确和符合实际 情形,并写出答案.
新浙教版《数学》七年级(上) 5.4一元一次方程的应用(二)
---等积变形问题
我们小学里学过的几个重要的周长、体积计算公式长方形周长:圆柱的体积:长方体的体积:C=2(a+b)V=sh=πr2hV=abh梯形的面积:S=(a+b)×c÷2想一想:请指出下列过程中,哪些量发生了变化,哪些量保持不变?
1、把一小杯水倒入另一只大杯中;
2、用一根15cm长的铁丝围成一个三角形,然后把它围成长方形;
3、用一块橡皮泥先做成一个立方体,再把它改变成球。解:水的底面积、高度发生了变化,水的体积保持不变 解:围成的图形的面积发生了变化,但铁丝的长度不变 解:形状改变,体积不变2(x+ x)=60解:设长为x cm,则宽为 cm,根据题意,得 若用一根长60cm的铁丝围成一个长方形 题中有什么等量关系?1、如果宽是长的 , 求这个长方形的长和
宽?(只需列出方程)
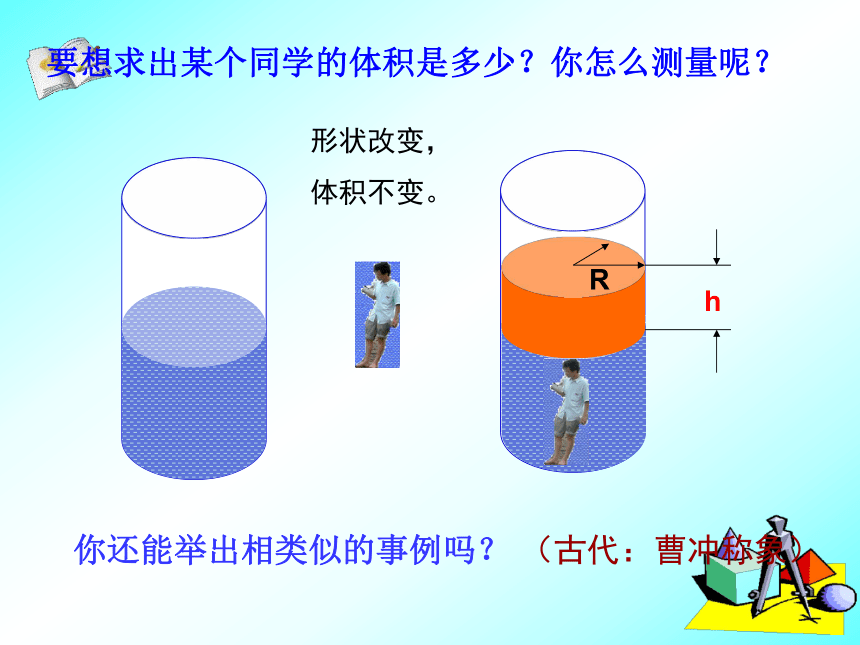
长方形的周长=铁丝的长度2、同样60厘米长的铁丝围成一个长方形,如果宽比长少12厘米,求这个长方形的面积.解:设长为xcm,则宽为(x-12)cm,根据题意,得2[x+(x-12)]=60解这个方程得 x=21所以这个长方形的长为21cm,宽为21-12=9cm长方形面积=21×9=189(cm2)本题中有哪些等量关系?长方形的周长=铁丝的长度hR要想求出某个同学的体积是多少?你怎么测量呢?你还能举出相类似的事例吗?(古代:曹冲称象)形状改变,
体积不变。例1:一纪念碑建筑的底面呈正方形,其四周铺上花岗石,形成一个宽为3.2米的正方形边框(如图中阴影部分),已知铺这个边框恰好用了144块边长为0.8米的正方形花岗石(接缝忽略不计),问纪念碑建筑底面的边长是多少米?1、题目中“纪念碑的底面呈正方形” 指的是哪个正方形?2、“形成一个宽为3.2米的正方形边框”问3.2米的边框指的是哪一段?例1:一纪念碑建筑的底面呈正方形,其四周铺上花岗石,形成一个宽为3.2米的正方形边框(如图中阴影部分),已知铺这个边框恰好用了144块边长为0.8米的正方形花岗石(接缝忽略不计),问纪念碑建筑底面的边长是多少米?3、图中阴影部分面积用144块边长为0.8米正方形花岗石铺成,那怎么求这个阴影部分的面积?4、如图,如果用x表示中间空白正方形的边长,怎么样用含x的代数式表示阴影部分的面积?你有几种方法?5、本题的等量关系是什么?144×0.8×0.86、请列出方程解答1、在应用方程解决有关实际问题时,清楚地分辨量之间的关系,尤其相等关系是建立方程的关键。
2、解题中的检验对确保答案的正确和合理很有帮助,但具体过程可省略不写。
3、对于这一类问题,就是用不同的方法来计算阴影部分的面积,用面积不变来列方程计算。
本题中有什么等量关系? 把一块梯形空地改成宽为30米的长方形运动场,要求面积不变,则应将原梯形的上、下底边作怎样的调整?
改造前的梯形的面积=改造后的长方形的面积解:设长方形的长为x米,根据题意,得30x=(30+60)×30÷2解这个方程,得 x=45 60-45=15(米)45-30=15(米)答:应将梯形的上底边缩短15米,下底边延长15米。1.一书架能放厚为6.3cm 的书45本.现在准备 放厚为2.1cm 的书,问能放这种书多少本?练一练2、一种小麦磨成面粉后,质量将减少15%,为了得到5100千克面粉,需多少千克小麦?例2 如图所示,用直径200mm的钢柱锻造一块长、宽、高分别为300mm,300mm和80mm的长方体毛胚底板,问应截取钢柱多少长(不计损耗,结果误差不超过1mm)1、在这个问题中的相等关系是:
圆柱的体积长方体的体积2、如果设锻造前圆柱的高为x毫米,也既截取的圆柱长为x毫米,则圆柱的体积怎么表示?3、锻造后长方体的长为( )毫米,宽为( )毫米,高为( )毫米,体积怎么计算?V=x×π×1002300300804、请列出方程解答锻造前的( )=锻造后的( ) 有一个底面直径是20cm,高9cm的形圆柱,工人叔叔要把它锻造成地面直径是10cm的形圆柱,工人叔叔想知道锻造后的圆柱有多少高?你能告诉他吗?2、根据这个等量关系怎样列方程?1、本题中有什么等量关系?锻造前圆柱的体积=锻造后圆柱的体积解:设锻造后圆柱高为x厘米,根据题意,得π×102×9=π×52×解这个方程,得 x=36答:锻造后圆柱的高为36厘米 如图,有A,B两个圆柱形容器,B容器的底面积为5平方厘米,A容器的底面积是B容器底面积的2倍,B容器的壁高为22cm。已知A容器内装水的高度为10cm,若把这些水倒入B容器,水会溢出吗?AB 如图,有A,B两个圆柱形容器,A容器的底面积是B容器底面积的2倍,B容器的壁高为22cm。已知A容器内装水的高度为10cm,若把这些水倒入B容器,水会溢出吗?AB如图一个铁片长30cm,宽20cm,打算从四个角各截去一个小正方形,然后把四边折起来做一个无盖的铁盒,铁盒的底面周长为60cm,问铁盒的高是多少? 30cm20cm课后拓展如图一个铁片长30cm,宽20cm,打算从四个角各截去一个小正方形,然后把四边折起来做一个无盖的铁盒,铁盒的底面周长为60cm,问铁盒的高是多少? 30-2x20-2xx相等关系:铁盒的底面周长=60cm30-2x20-2x课后拓展4.按图示的方法搭1个三角形需要3根火柴棒,搭2个三角形需要5根火柴棒.设共搭成n 个三角形,你怎样用关于是 n 的代数式表示n 个三角形需要火柴棒的根数? 现有2009根火柴棒,能搭几个这样的三角形? 2100根呢?本节课同学们学到些什么?小结:利用图形变形前后面积,体积,周长不变,进行列方程。
( 例如 ) ;其它的量用含x的代数式表示出来根据相等关系列出方程;求出未知数的值;
检查求得的值是否正确和符合实际 情形,并写出答案.
新浙教版《数学》七年级(上) 5.4一元一次方程的应用(二)
---等积变形问题
我们小学里学过的几个重要的周长、体积计算公式长方形周长:圆柱的体积:长方体的体积:C=2(a+b)V=sh=πr2hV=abh梯形的面积:S=(a+b)×c÷2想一想:请指出下列过程中,哪些量发生了变化,哪些量保持不变?
1、把一小杯水倒入另一只大杯中;
2、用一根15cm长的铁丝围成一个三角形,然后把它围成长方形;
3、用一块橡皮泥先做成一个立方体,再把它改变成球。解:水的底面积、高度发生了变化,水的体积保持不变 解:围成的图形的面积发生了变化,但铁丝的长度不变 解:形状改变,体积不变2(x+ x)=60解:设长为x cm,则宽为 cm,根据题意,得 若用一根长60cm的铁丝围成一个长方形 题中有什么等量关系?1、如果宽是长的 , 求这个长方形的长和
宽?(只需列出方程)
长方形的周长=铁丝的长度2、同样60厘米长的铁丝围成一个长方形,如果宽比长少12厘米,求这个长方形的面积.解:设长为xcm,则宽为(x-12)cm,根据题意,得2[x+(x-12)]=60解这个方程得 x=21所以这个长方形的长为21cm,宽为21-12=9cm长方形面积=21×9=189(cm2)本题中有哪些等量关系?长方形的周长=铁丝的长度hR要想求出某个同学的体积是多少?你怎么测量呢?你还能举出相类似的事例吗?(古代:曹冲称象)形状改变,
体积不变。例1:一纪念碑建筑的底面呈正方形,其四周铺上花岗石,形成一个宽为3.2米的正方形边框(如图中阴影部分),已知铺这个边框恰好用了144块边长为0.8米的正方形花岗石(接缝忽略不计),问纪念碑建筑底面的边长是多少米?1、题目中“纪念碑的底面呈正方形” 指的是哪个正方形?2、“形成一个宽为3.2米的正方形边框”问3.2米的边框指的是哪一段?例1:一纪念碑建筑的底面呈正方形,其四周铺上花岗石,形成一个宽为3.2米的正方形边框(如图中阴影部分),已知铺这个边框恰好用了144块边长为0.8米的正方形花岗石(接缝忽略不计),问纪念碑建筑底面的边长是多少米?3、图中阴影部分面积用144块边长为0.8米正方形花岗石铺成,那怎么求这个阴影部分的面积?4、如图,如果用x表示中间空白正方形的边长,怎么样用含x的代数式表示阴影部分的面积?你有几种方法?5、本题的等量关系是什么?144×0.8×0.86、请列出方程解答1、在应用方程解决有关实际问题时,清楚地分辨量之间的关系,尤其相等关系是建立方程的关键。
2、解题中的检验对确保答案的正确和合理很有帮助,但具体过程可省略不写。
3、对于这一类问题,就是用不同的方法来计算阴影部分的面积,用面积不变来列方程计算。
本题中有什么等量关系? 把一块梯形空地改成宽为30米的长方形运动场,要求面积不变,则应将原梯形的上、下底边作怎样的调整?
改造前的梯形的面积=改造后的长方形的面积解:设长方形的长为x米,根据题意,得30x=(30+60)×30÷2解这个方程,得 x=45 60-45=15(米)45-30=15(米)答:应将梯形的上底边缩短15米,下底边延长15米。1.一书架能放厚为6.3cm 的书45本.现在准备 放厚为2.1cm 的书,问能放这种书多少本?练一练2、一种小麦磨成面粉后,质量将减少15%,为了得到5100千克面粉,需多少千克小麦?例2 如图所示,用直径200mm的钢柱锻造一块长、宽、高分别为300mm,300mm和80mm的长方体毛胚底板,问应截取钢柱多少长(不计损耗,结果误差不超过1mm)1、在这个问题中的相等关系是:
圆柱的体积长方体的体积2、如果设锻造前圆柱的高为x毫米,也既截取的圆柱长为x毫米,则圆柱的体积怎么表示?3、锻造后长方体的长为( )毫米,宽为( )毫米,高为( )毫米,体积怎么计算?V=x×π×1002300300804、请列出方程解答锻造前的( )=锻造后的( ) 有一个底面直径是20cm,高9cm的形圆柱,工人叔叔要把它锻造成地面直径是10cm的形圆柱,工人叔叔想知道锻造后的圆柱有多少高?你能告诉他吗?2、根据这个等量关系怎样列方程?1、本题中有什么等量关系?锻造前圆柱的体积=锻造后圆柱的体积解:设锻造后圆柱高为x厘米,根据题意,得π×102×9=π×52×解这个方程,得 x=36答:锻造后圆柱的高为36厘米 如图,有A,B两个圆柱形容器,B容器的底面积为5平方厘米,A容器的底面积是B容器底面积的2倍,B容器的壁高为22cm。已知A容器内装水的高度为10cm,若把这些水倒入B容器,水会溢出吗?AB 如图,有A,B两个圆柱形容器,A容器的底面积是B容器底面积的2倍,B容器的壁高为22cm。已知A容器内装水的高度为10cm,若把这些水倒入B容器,水会溢出吗?AB如图一个铁片长30cm,宽20cm,打算从四个角各截去一个小正方形,然后把四边折起来做一个无盖的铁盒,铁盒的底面周长为60cm,问铁盒的高是多少? 30cm20cm课后拓展如图一个铁片长30cm,宽20cm,打算从四个角各截去一个小正方形,然后把四边折起来做一个无盖的铁盒,铁盒的底面周长为60cm,问铁盒的高是多少? 30-2x20-2xx相等关系:铁盒的底面周长=60cm30-2x20-2x课后拓展4.按图示的方法搭1个三角形需要3根火柴棒,搭2个三角形需要5根火柴棒.设共搭成n 个三角形,你怎样用关于是 n 的代数式表示n 个三角形需要火柴棒的根数? 现有2009根火柴棒,能搭几个这样的三角形? 2100根呢?本节课同学们学到些什么?小结:利用图形变形前后面积,体积,周长不变,进行列方程。
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
