5.4.4一元一次方程的应用(四)工程问题与打折问题
文档属性
| 名称 | 5.4.4一元一次方程的应用(四)工程问题与打折问题 |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-29 22:06:11 | ||
图片预览








文档简介
课件24张PPT。运用方程解决实际问题的一般过程:审设列解验前面学了哪几种类型?---行程问题---等积变形问题---调配问题一元一次方程的应用(四)打折问题工程问题工程问题基 础 练 习1、甲每天生产某种零件80个,3天能生产 个零件。
2、乙每天生产某种零件x个,5天能生产 个零件。
3、甲每天生产某种零件80个,乙每天生产某种零件x个。
他们5天一共生产 个零件。
工程问题的基本数量关系:(1)工作总量=工作时间×工作效率3×805x(5×80+5x)工作效率=工作总量————工作时间工作时间=工作总量————工作效率(2)甲、乙合作的工作效率
=甲队工作效率+乙队工作效率4、一批零件,甲每小时能加工80个,则
⑴甲x小时可加工 个零件。⑵加工a个零件,甲需 小时完成。5、一项工程甲独做需6天完成,则⑴甲独做一天可完成这项工程的⑵若乙独做比甲快2天完成,则乙独做一天可完成
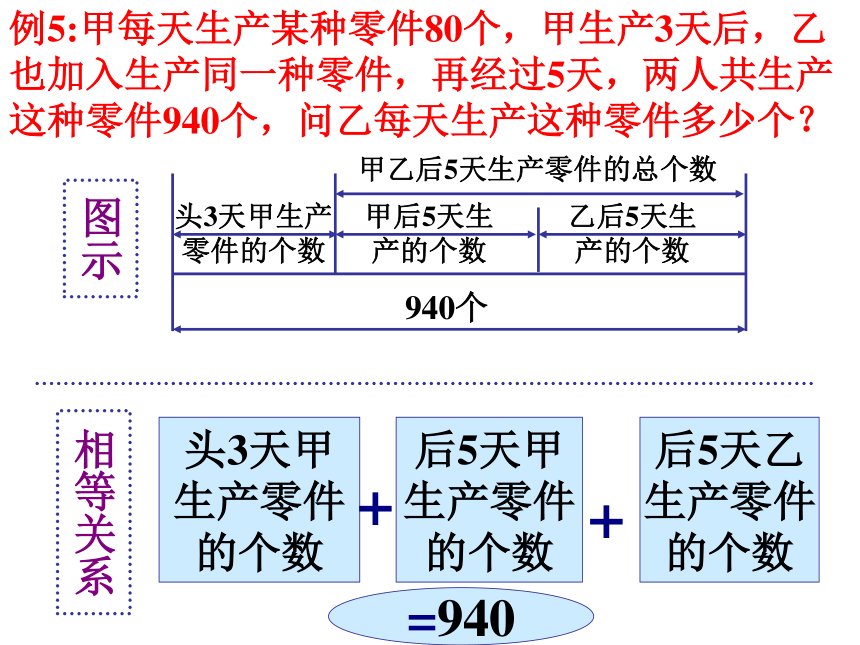
这项工程的80x当问题中的工作量没有具体数值时,常设总工作量为1头3天甲生产
零件的个数甲乙后5天生产零件的总个数甲后5天生
产的个数乙后5天生
产的个数图示5、甲每天生产某种零件80个,乙每天生产这种零件x个,甲生产3天后,乙也加入生产同一种零件,再经过5天,两人共生产 个零件。
(3×80+5×80+5x)(3)全部工作量=各队工作量之和头3天甲生产
零件的个数甲乙后5天生产零件的总个数甲后5天生
产的个数乙后5天生
产的个数940个图示相等关系头3天甲
生产零件
的个数+后5天甲
生产零件
的个数后5天乙
生产零件
的个数+=940例5:甲每天生产某种零件80个,甲生产3天后,乙也加入生产同一种零件,再经过5天,两人共生产这种零件940个,问乙每天生产这种零件多少个?练习1、修筑一条公路,甲工程队单独承包要80天完成,乙工程队
单独承包要120天完成
1)现在由两个工程队合作承包,几天可以完成?
2)如果甲、乙两工程队合作了30天后,因甲工作队另有任务,
剩下工作由乙工作队完成,则修好这条公路共需要几天?
解: 1)设两工程队合作需要x天完成。
2)设修好这条公路共需要 y 天完成。
等量关系: 甲30天工作量+乙队y天的工作量 = 1
答:两工程队合作需要48天完成,修好这条公路还需75天。等量关系:甲工作量+乙工作量=1
依题意得
依题意得y=75x=48(1)可否用示意图来分析数量关系?(2)总工作量怎么表示?甲乙两人的工作
效率怎么表示?(3)设哪个未知数?相关的量怎样用它表示?(4)根据怎样的数量关系列方程?练习2、一件工作,甲单独做20个小时完成,
乙单独做12小时完成,现在先由甲单独做4小
时,剩下的部分由甲、乙合做。剩下的部分
需要几小时完成?相等关系:全部工作量=甲独做工作量+甲、乙合作工作量
练习2、一件工作,甲单独做20个小时完成,乙单独做12小时完成,现在先由甲单独做4小时,剩下的部分由甲、乙合做。剩下的部分需要几小时完成?解:设剩下的部分需要x小时完成,根据题意,
得
解这个方程,得x=6
答:剩下的部分需要6小时完成。3.一收割机队每天收割小麦12公顷,收割完一片麦地的 后,该收割机改进操作,效率提高到原来的 倍,因此比预定时间提早1天完成.问这片麦地 有多少公顷? 解:设这片麦地 有X公顷,由题意得检验:x=180适合方程,且符合题意.
答:这片麦地 有180公顷课后习题大亏本大放血5折酬宾清仓处理跳楼价打折销售问题1.一件商品的销售价为100元,买入价为90元,则毛利润为 元。
2. 某商品的原价是x元,若按七五折出售,售价是 。
3.一件夹克成本价为50元,提价50%后标价,再按标价的8折出售,则售价为 元。 打折销售10600.75x1、500元的9折价是______元 ,x折是_______元.
2、某商品的每件销售利润是72元,进价是120,
则售价是__________元.
3、某商品利润率13﹪,进价为50元,则利润是
________元.试一试利润 = 售价-进价打 x 折的售价= 利润率 = 原价×4501926.5×100%?想一想 王洁做服装生意。她进了一批运动衫,每件进价90元,卖出时每件100元。请问一件运动衫利润是多少元?利润率又是多少?进价:90元。售价:100元。利润:(100 – 90)元 = 10元。做一做1、一件商品的进价为45元,利润为10元,
则售价为 ; 2、一件商品的标价为50元,现以八折销售,则售价
为 ,若进价为33元,则它的利润为 ;3、一块手表的成本价是70元,利润率是30%,则这
块手表的利润是 ,售价是 ; 4、某商品的原价是a元,提价10%后再降价10%,
这时这件商品的价格是( )列式:a(1+10%)(1-10%)=0.99a55元40元7元21元91元C讲解 例1 商店对某种商品作调价,按原价的8折出售,此时商品的利润率是10%,此商品的进价为1600元。问商品的原价是多少?根据题意找出等量关系:已知为:10%已知:1600元商品原价 × 80%已知:1600元如果设商品原价为x,则根据等量关系可得方程:10% 例 商店对某种商品作调价,按原价的8折出售,此时商品的利润率是10%,此商品的进价为1600元。商品的原价是多少?解:设此商品的原价为x元,根据题意,得X· 80%- 16001600=10%去分母X· 80%- 1600 =10%× 1600移项x ·80% =10% ×1600 +1600合并同类项x ·80%= 1760系数化为1x =2200答:此商品的原价为2200元。1.一件商品按成本价提高30%后标价,又以8折销售,售价为208元,这种商品的成本价是多少元?解:设成本价为x元,由题意得检验:x=200适合方程,且符合题意.
答:这种商品的成本价是200元.课后习题课内练习:1.某种商品的进价是每件400元,原标价为每件600元。商店打折销售该商品时的毛利率为5%,问该商品是打几折销售的? 5、某商店有两种不同型号的计算器的出售价都是64元,
卖出其中一种计算器商店盈利为进货价的60%,卖出另
一种计算器商店亏损进货价的20%。若卖出这两种计算器1台,这家商店的盈亏情况如何?
解:设第一种计算器进货价为X元,由题意得60%X+X=64
解得:X=40设另一种种计算器进货价为y元,由题意得(1—20%)y=64
解得:y=80答:商店盈利8元.销售中的盈亏本节课你学到了什么?1.工程问题的基本数量关系:合作交流工作总量=工作效率×工作时间各队合作工作效率=各队工作效率之和全部工作量之和=各队工作量之和当问题中的工作量没有具体数值时,设总工作量为1 2.有关利润方面的应用题,主要有四个量:
(1)进价
(2)售价(或打折售价)
(3)利润
(4)利润率。
2、乙每天生产某种零件x个,5天能生产 个零件。
3、甲每天生产某种零件80个,乙每天生产某种零件x个。
他们5天一共生产 个零件。
工程问题的基本数量关系:(1)工作总量=工作时间×工作效率3×805x(5×80+5x)工作效率=工作总量————工作时间工作时间=工作总量————工作效率(2)甲、乙合作的工作效率
=甲队工作效率+乙队工作效率4、一批零件,甲每小时能加工80个,则
⑴甲x小时可加工 个零件。⑵加工a个零件,甲需 小时完成。5、一项工程甲独做需6天完成,则⑴甲独做一天可完成这项工程的⑵若乙独做比甲快2天完成,则乙独做一天可完成
这项工程的80x当问题中的工作量没有具体数值时,常设总工作量为1头3天甲生产
零件的个数甲乙后5天生产零件的总个数甲后5天生
产的个数乙后5天生
产的个数图示5、甲每天生产某种零件80个,乙每天生产这种零件x个,甲生产3天后,乙也加入生产同一种零件,再经过5天,两人共生产 个零件。
(3×80+5×80+5x)(3)全部工作量=各队工作量之和头3天甲生产
零件的个数甲乙后5天生产零件的总个数甲后5天生
产的个数乙后5天生
产的个数940个图示相等关系头3天甲
生产零件
的个数+后5天甲
生产零件
的个数后5天乙
生产零件
的个数+=940例5:甲每天生产某种零件80个,甲生产3天后,乙也加入生产同一种零件,再经过5天,两人共生产这种零件940个,问乙每天生产这种零件多少个?练习1、修筑一条公路,甲工程队单独承包要80天完成,乙工程队
单独承包要120天完成
1)现在由两个工程队合作承包,几天可以完成?
2)如果甲、乙两工程队合作了30天后,因甲工作队另有任务,
剩下工作由乙工作队完成,则修好这条公路共需要几天?
解: 1)设两工程队合作需要x天完成。
2)设修好这条公路共需要 y 天完成。
等量关系: 甲30天工作量+乙队y天的工作量 = 1
答:两工程队合作需要48天完成,修好这条公路还需75天。等量关系:甲工作量+乙工作量=1
依题意得
依题意得y=75x=48(1)可否用示意图来分析数量关系?(2)总工作量怎么表示?甲乙两人的工作
效率怎么表示?(3)设哪个未知数?相关的量怎样用它表示?(4)根据怎样的数量关系列方程?练习2、一件工作,甲单独做20个小时完成,
乙单独做12小时完成,现在先由甲单独做4小
时,剩下的部分由甲、乙合做。剩下的部分
需要几小时完成?相等关系:全部工作量=甲独做工作量+甲、乙合作工作量
练习2、一件工作,甲单独做20个小时完成,乙单独做12小时完成,现在先由甲单独做4小时,剩下的部分由甲、乙合做。剩下的部分需要几小时完成?解:设剩下的部分需要x小时完成,根据题意,
得
解这个方程,得x=6
答:剩下的部分需要6小时完成。3.一收割机队每天收割小麦12公顷,收割完一片麦地的 后,该收割机改进操作,效率提高到原来的 倍,因此比预定时间提早1天完成.问这片麦地 有多少公顷? 解:设这片麦地 有X公顷,由题意得检验:x=180适合方程,且符合题意.
答:这片麦地 有180公顷课后习题大亏本大放血5折酬宾清仓处理跳楼价打折销售问题1.一件商品的销售价为100元,买入价为90元,则毛利润为 元。
2. 某商品的原价是x元,若按七五折出售,售价是 。
3.一件夹克成本价为50元,提价50%后标价,再按标价的8折出售,则售价为 元。 打折销售10600.75x1、500元的9折价是______元 ,x折是_______元.
2、某商品的每件销售利润是72元,进价是120,
则售价是__________元.
3、某商品利润率13﹪,进价为50元,则利润是
________元.试一试利润 = 售价-进价打 x 折的售价= 利润率 = 原价×4501926.5×100%?想一想 王洁做服装生意。她进了一批运动衫,每件进价90元,卖出时每件100元。请问一件运动衫利润是多少元?利润率又是多少?进价:90元。售价:100元。利润:(100 – 90)元 = 10元。做一做1、一件商品的进价为45元,利润为10元,
则售价为 ; 2、一件商品的标价为50元,现以八折销售,则售价
为 ,若进价为33元,则它的利润为 ;3、一块手表的成本价是70元,利润率是30%,则这
块手表的利润是 ,售价是 ; 4、某商品的原价是a元,提价10%后再降价10%,
这时这件商品的价格是( )列式:a(1+10%)(1-10%)=0.99a55元40元7元21元91元C讲解 例1 商店对某种商品作调价,按原价的8折出售,此时商品的利润率是10%,此商品的进价为1600元。问商品的原价是多少?根据题意找出等量关系:已知为:10%已知:1600元商品原价 × 80%已知:1600元如果设商品原价为x,则根据等量关系可得方程:10% 例 商店对某种商品作调价,按原价的8折出售,此时商品的利润率是10%,此商品的进价为1600元。商品的原价是多少?解:设此商品的原价为x元,根据题意,得X· 80%- 16001600=10%去分母X· 80%- 1600 =10%× 1600移项x ·80% =10% ×1600 +1600合并同类项x ·80%= 1760系数化为1x =2200答:此商品的原价为2200元。1.一件商品按成本价提高30%后标价,又以8折销售,售价为208元,这种商品的成本价是多少元?解:设成本价为x元,由题意得检验:x=200适合方程,且符合题意.
答:这种商品的成本价是200元.课后习题课内练习:1.某种商品的进价是每件400元,原标价为每件600元。商店打折销售该商品时的毛利率为5%,问该商品是打几折销售的? 5、某商店有两种不同型号的计算器的出售价都是64元,
卖出其中一种计算器商店盈利为进货价的60%,卖出另
一种计算器商店亏损进货价的20%。若卖出这两种计算器1台,这家商店的盈亏情况如何?
解:设第一种计算器进货价为X元,由题意得60%X+X=64
解得:X=40设另一种种计算器进货价为y元,由题意得(1—20%)y=64
解得:y=80答:商店盈利8元.销售中的盈亏本节课你学到了什么?1.工程问题的基本数量关系:合作交流工作总量=工作效率×工作时间各队合作工作效率=各队工作效率之和全部工作量之和=各队工作量之和当问题中的工作量没有具体数值时,设总工作量为1 2.有关利润方面的应用题,主要有四个量:
(1)进价
(2)售价(或打折售价)
(3)利润
(4)利润率。
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
