7.4一次函数的图象(2)(含答案解析)
文档属性
| 名称 | 7.4一次函数的图象(2)(含答案解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 60.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-30 00:00:00 | ||
图片预览


文档简介
7.4一次函数的图象(2)
【要点预习】
一次函数的性质:
对于一次函数y=kx+b(k, b为常数, 且k≠0). 当k>0时, y随x的增大而 ;当 时, y随x的增大而减小.
【课前热身】
1. 如果直线经过点(1,-3),则k= .
答案:-3
2. 一次函数y=2x+2的图象不经过第 象限.
答案:四
3. 一次函数y=2x+2中, y随着x的增大而 .
答案:增大
4. 请写出一个一次函数,使y随着x的增大而减小: .
答案:形如y=kx+b(k<0)
【讲练互动】
【例1】对于一次函数y=(m+4)x+2m-1,如果y随x增大而增大,且它的图象与y轴的交点在x轴下方,试求m的取值范围.
【分析】本题可利用了一次函数图象的性质来确定k、b符号,进而求得m的取值范围.
【解】∵一次函数y随x的增大而增大.∴ k=m+4>0,即m>-4.
又∵一次函数的图象与y轴的交点在x轴下方,
∴ b=2m-1<0,即.∴所求m的取值范围是.
【绿色通道】对于一次函数y=kx+b(k、b为常数,k0)当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小;b>0时,函数图象与y轴的交点在x轴上方,b<0时,函数图象与y轴的交点在x轴下方.
【变式训练】
1. 下列一次函数中,y随x的增大而减小的是…………………………………………( )
A. B. C. D.
【答案】B
【例2】某公司在甲、乙两座仓库分别有农用车12辆和6辆。现需要调往A县10辆,调往B县8辆,已知从甲仓库调运一辆农用车到A县和B县的运费分别为40元和80元;从乙仓库调运一辆农用车到A县和B县的运费分别为30元和50元.
(1)设从乙仓库调往A县和B县农用车x辆,求总运费y关于x的函数关系式
(2)若要求总运费 不超过900元,问共有几种调运方案?
(3)求出总运费最低的调运方案,最低运费是多少元?
【解】(1)y=30+50(6-x)+80(8-6+x)+40(12-2-x)=20x+860.
(2)20x+860≤900,x≤2. ∵0≤x≤6,∴0≤x≤2.
∵x为非负整数,所以x的取值为0,1,2. ∴共有三种调运方案.
(3)∵y=20x+860,且x的取值为0,1,2.
由一次函数的性质得x=0时,y的值最小,y最小=860(元).
此时的调运方案是:乙仓库的6辆全部运往B县,甲仓库的2辆运往B县,10辆运往A县,最低运费为860元.
【变式训练】
2.国家为了关心广大农民群众,增强农民抵御大病风险的能力,积极推行农村医疗保险制度,某县根据本地的实际情况,制定了纳入医疗保险的农民医疗费用报销规定.享受医保的农民可在定点医院就医,在规定的药品品种范围内用药,由患者先垫付医疗费用,年终到医保中心报销,医疗费的报销比例标准如下表:
费用范围
500元以下(含500元)
超过500元且不超过10000元的部分
超过10000元的部分
报销比例标准
不予报销
50%
60%
(1)设刘爷爷一年的实际医疗费为元(500
(3)若刘爷爷一年内自付医疗费不小于6250元,则刘爷爷当年实际医疗费至少为多少元?
解:(1) y=50%(x-500)=0.5x-250.
(2) 2000-(0.5×2000-250)=1250元.
(3) ∵10000-50%(10000-500)=5250<6250, ∴刘爷爷的实际医疗费超过10000元.
刘爷爷实际医疗费为x元, 则x-50%(10000-500)-60%(x-10000)=6250, 解得x=12500元.
【同步测控】
基础自测
1. 正比例函数y=(m-1)x的图象经过一、三象限,则m的取值范围是………………( )
A. B. C. D.
答案:B
2.已知正比例函数 的图象上两点A(,),B(,),当时,有,那么m的取值范围是………………………………………………………( )
A. B. .C. D.
答案:A
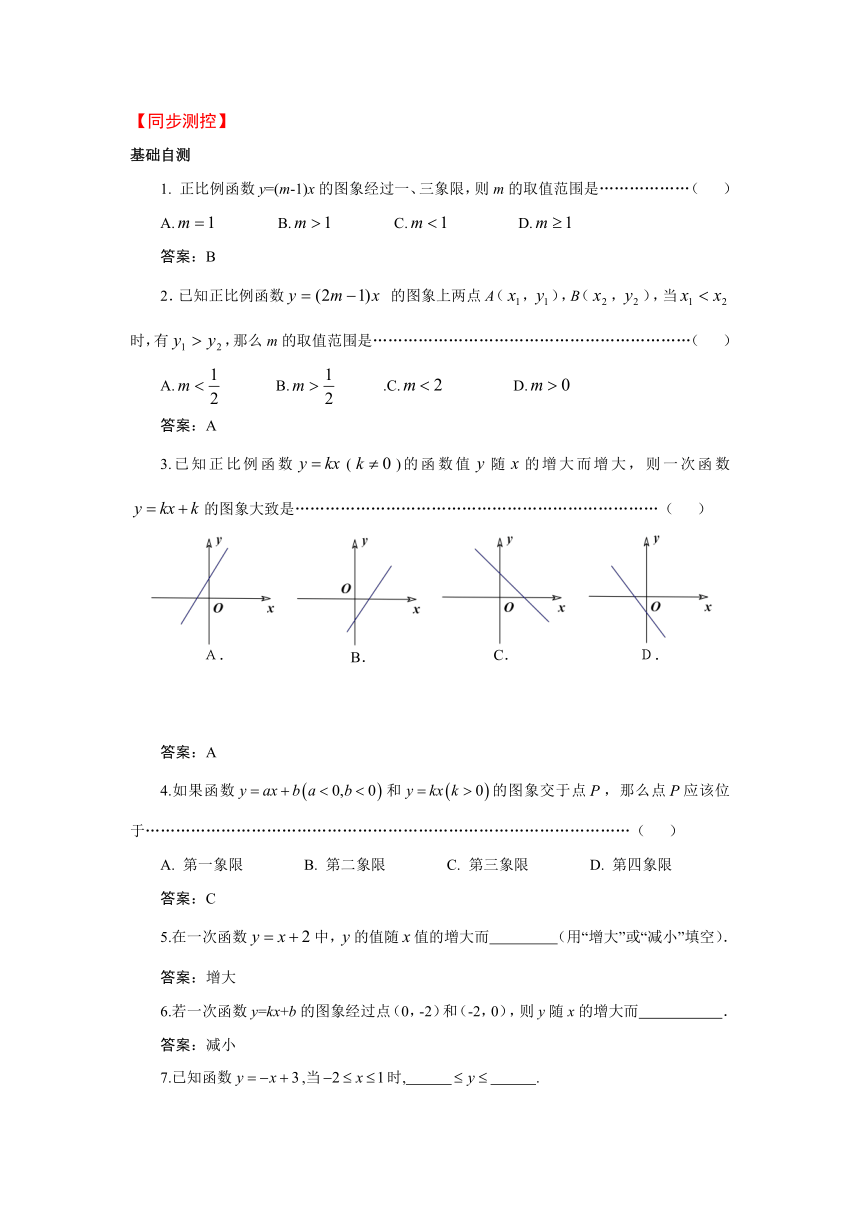
3.已知正比例函数()的函数值随的增大而增大,则一次函数的图象大致是………………………………………………………………( )
答案:A
4.如果函数和的图象交于点,那么点应该位于……………………………………………………………………………………( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
答案:C
5.在一次函数中,的值随值的增大而 (用“增大”或“减小”填空).
答案:增大
6.若一次函数y=kx+b的图象经过点(0,-2)和(-2,0),则y随x的增大而 .
答案:减小
7.已知函数,当时, .
答案:2 5
8.一次函数具有下列性质:①图像经过点;②当时,函数值随自变量的增大而增大.满足上述两条性质的函数解析式可以是 (只要求写一个).
答案:形如y=kx+k+2(k<0).
9. 已知某种商品的进价为168元, 售价的10%用于缴税和其它费用.若要使纯利润保持在售价的10%—20%之间(包括10%和20%), 问怎么确定售价?
解:设商品的售价为x元, 纯利润为y元, 则y=x-10%x-168=0.9x-168.
∵10%x≤y≤20%x, ∴0.1x≤0.9x-168≤0.2x, 解得210≤x≤240.
10.康乐公司在A、B两地分别有同型号的机器17台和15台,现要运往甲地18台,乙地14台. 从A、B两地运往甲、乙两地的费用如下表:
甲地(元/台)
乙地(元/台)
A地
600
500
B地
400
800
(1) 如果从A地运往甲地x台,求完成以上调运所需总费用y(元)与x(台)的函数关系式;
(2)若康乐公司请你设计一种最佳调运方案,使总的费用最少,该公司完成以上调运方案至少需要多少费用?为什么?
分析:对于(1), 由于从A地运往甲地x台, 故从A地运往乙地(17-x)台, 从B地运往甲地(18-x)台, 从B地运往乙地14-(18-x)=(x-4)台, 再根据表格中的运费可求出y与x的函数关系式;对于(2)可通过求x的取值范围及一次函数的增减性来求得.
解:(1) y=600x+500(17-x)+400(18-x)+800(x-4)=500x+12500;
(2) ∵, ∴4≤x≤17. 又k=500>0, ∴y随x的增大而增大.
∴x=4时, y最小=14500元.
此时,从A地运往甲地4台,运往乙地13台,从B地运往甲地14台,从B地运往乙地0台.
能力提升
11.若直线y=kx+b(k0)经过一、二、四象限,则k、b的符号分别为………………( )
A. k>0,b>0 B. k>0,b<0 C. k<0,b>0 D. k<0,b<0
答案:C
12.如图,函数在直角坐标系中的图象可能是……( )
答案:B
13.若有意义,则函数y=kx-1的图象不经过第 象限.
答案:二
14. 科学家通过实验探究出一定质量的某气体在体积不变的情况下,压强P(千帕)随温度t(℃)变化的函数关系式是P=kt+b,其图象如图所示的射线AB.
(1)根据图象求出上述气体的压强P与温度t的函数关系式;
(2)求出当压强P为200千帕时,上述气体的温度.
解:(1)∵函数P=kt+b的图象过点(0,100),(25,110),
∴ 解之,得 ∴(t≥0).
(2) 当P=200时,由(1)得.解得t=250.
即当压强为200千帕时,气体的温度是250℃.
15.某车间有20名工人,每人每天可加工甲种零件5个或乙种零件4个,每加工一个甲种零件可获利16元,每加工一个乙种零件可获利24元.现要求加工甲种零件的人数不少于加工乙种零件人数的2倍,设每天所获利润为元,那么多少人加工甲种零件时,每天所获利润最大?每天所获最大利润是多少元?
解:设有x人加工甲种零件, 则加工乙种零件的有(20-x)人.
由题意,得y=16x+24(20-x)=-8x+480.
∵20≥x≥2(20-x), ∴≤x≤20. 且k=-8<0, ∴y随x的增大而减小.
∴当x=14时, y最大=368元. 即14人加工甲种零件时, 最大利润为368元.
创新应用
16.已知某函数图象关于直线x=1对称,其中一部分图象如图所示,点A(x1,y1),点B(x2,y2)在函数图象上,且-1
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
