7.5一次函数的简单应用(1)(含答案解析)
文档属性
| 名称 | 7.5一次函数的简单应用(1)(含答案解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 147.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-30 00:00:00 | ||
图片预览


文档简介
7.5一次函数的简单应用(1)
【要点预习】
利用图象取得函数解析式的基本步骤:
(1) 通过实验、测量获得数量足够多的 的对应值;
(2) 建立合适的直角坐标系, 在坐标系内以各对应值为坐标描点, 并用 法画出函数图象;
(3) 观察图象特征, 判定函数的 .
【课前热身】
1. 直线y=2x-1经过的点是……………………………………………………………( )
A. (2,1) B. (0,1) C. (2,0) D. (1,1)
答案:D
2. 给出下列函数:① ② ③;④.其中随着的增大而增大的是………………………………………………………………………………( )
A. ①② B. ③④ C. ①③ D. ②④
答案:C
3. 已知关于x的一次函数y=mx+1,如果y随x的增大而减小, 则m的取值范围是…( )
A. m>0 B. m<0 C.m≥0 D.m≤0
答案:B
4. 正比例函数的图象经过第一、三象限,则k的取值范围为 .
答案:k>3
【讲练互动】
【例1】如图所示,是某学校一电热淋浴器水箱的水量y(升)与供水时间x(分)的函数关系.
(1) 求y与x的函数关系式;
(2) 在(1)的条件下,求在30分钟时水箱有多少升水?
【解】(1) 由图可知y与x的函数关系是一次函数,设y=kx+b.
根据题意,得解得∴(10≤x≤50).
(2) 当x=30时,(升), ∴在30分钟时水箱有100升水.
【变式训练】
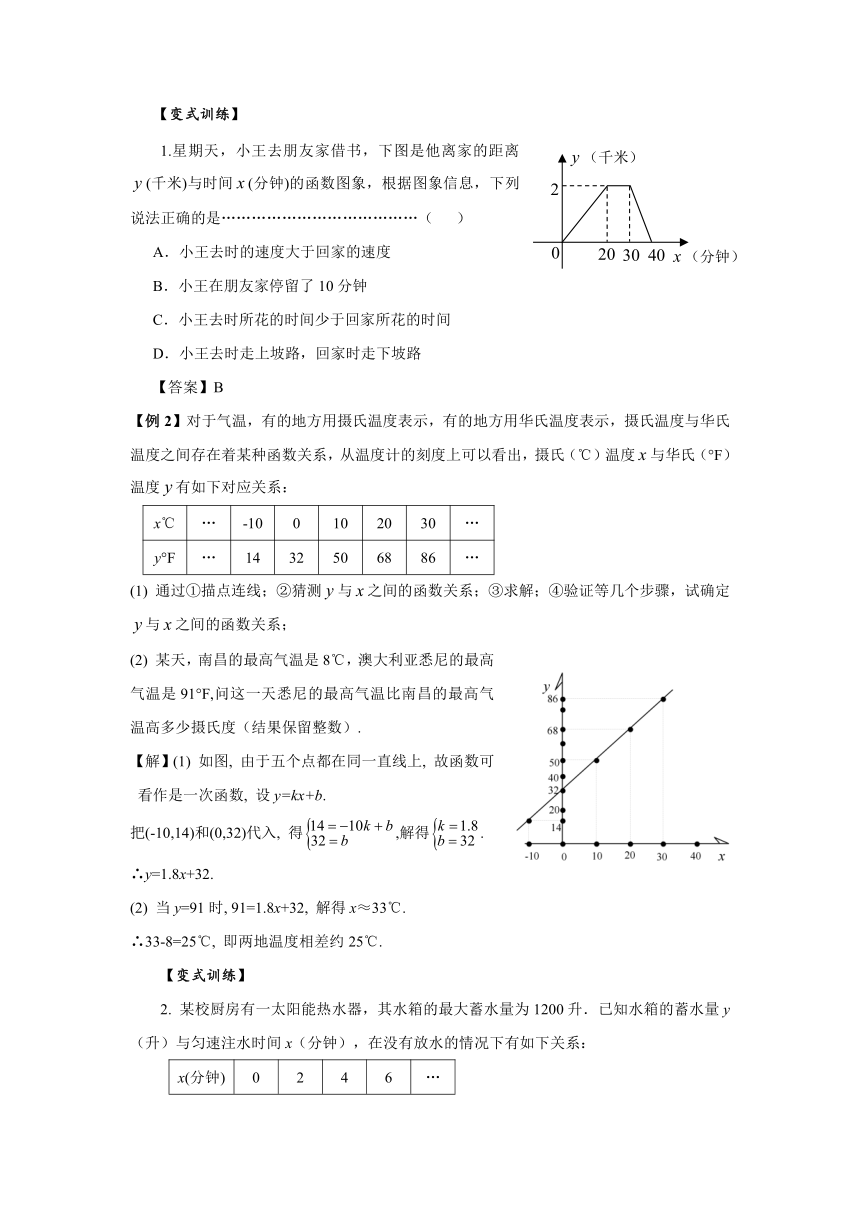
1.星期天,小王去朋友家借书,下图是他离家的距离(千米)与时间(分钟)的函数图象,根据图象信息,下列说法正确的是…………………………………( )
A.小王去时的速度大于回家的速度
B.小王在朋友家停留了10分钟
C.小王去时所花的时间少于回家所花的时间
D.小王去时走上坡路,回家时走下坡路
【答案】B
【例2】对于气温,有的地方用摄氏温度表示,有的地方用华氏温度表示,摄氏温度与华氏温度之间存在着某种函数关系,从温度计的刻度上可以看出,摄氏(℃)温度与华氏(°F)温度有如下对应关系:
x℃
…
-10
0
10
20
30
…
y°F
…
14
32
50
68
86
…
(1) 通过①描点连线;②猜测与之间的函数关系;③求解;④验证等几个步骤,试确定与之间的函数关系;
(2) 某天,南昌的最高气温是8℃,澳大利亚悉尼的最高气温是91°F,问这一天悉尼的最高气温比南昌的最高气温高多少摄氏度(结果保留整数).
【解】(1) 如图, 由于五个点都在同一直线上, 故函数可看作是一次函数, 设y=kx+b.
把(-10,14)和(0,32)代入, 得,解得.
∴y=1.8x+32.
(2) 当y=91时, 91=1.8x+32, 解得x≈33℃.
∴33-8=25℃, 即两地温度相差约25℃.
【变式训练】
2. 某校厨房有一太阳能热水器,其水箱的最大蓄水量为1200升.已知水箱的蓄水量y(升)与匀速注水时间x(分钟),在没有放水的情况下有如下关系:
x(分钟)
0
2
4
6
…
y(升)
0
80
160
240
…
(1) 根据上表中的数据,在上图的坐标系中描出相应的各点,顺次连结各点后,你发现这些点在哪一种图形上?猜一猜,符合这个图形的函数解析式;
(2) 请验证上表各点的坐标是否满足函数解析式,归纳你的结论,并写出自变量x的取值范围.
【解】(1)描点连结如图, 发现四个点在经过原点的一条直线上, 可以猜想函数解析式为y=kx.
(2) 把(2, 80)代入解析式, 得k=40, ∴y=40x(x≥0).
经验证, 其余各点均在y=40x上.
【同步测控】
基础自测
1. 在一次函数y=(2m+2)x+5中, y随x的增大而减小, 那么…………………………( )
A. m<-1 B.m>-1 C.m=1 D.m<1
答案:A
2. 某天早晨,小强从家出发,以v1的速度前往学校,途中在一饮食店吃早点,之后,以v2的速度向学校行进.已知v1>v2,下面的图象中表示小强从家到学校的时间t(分钟)与路程s(千米)之间的关系是……………………………………………………………………( )
答案:A
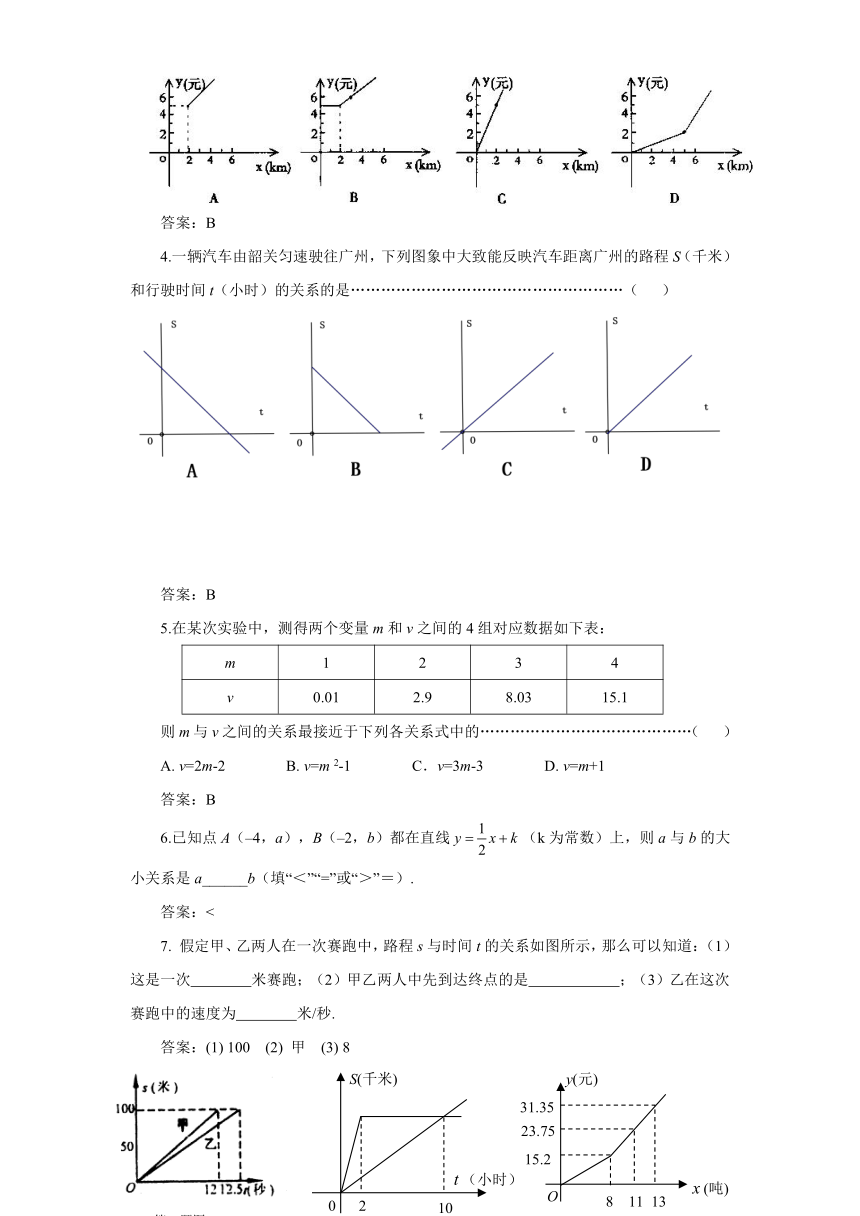
3.永州市内货摩(运货的摩托)的运输价格为:2千米内运费5元;路程超过2千米的,每超过1千米增加运费1元,那么运费y元与运输路程x千米的函数图象是…( )
答案:B
4.一辆汽车由韶关匀速驶往广州,下列图象中大致能反映汽车距离广州的路程S(千米)和行驶时间t(小时)的关系的是………………………………………………( )
答案:B
5.在某次实验中,测得两个变量m和v之间的4组对应数据如下表:
m
1
2
3
4
v
0.01
2.9
8.03
15.1
则m与v之间的关系最接近于下列各关系式中的……………………………………( )
A. v=2m-2 B. v=m 2-1 C.v=3m-3 D. v=m+1
答案:B
6.已知点A(–4,a),B(–2,b)都在直线(k为常数)上,则a与b的大小关系是a______b(填“<”“=”或“>”=).
答案:<
7. 假定甲、乙两人在一次赛跑中,路程s与时间t的关系如图所示,那么可以知道:(1)这是一次 米赛跑;(2)甲乙两人中先到达终点的是 ;(3)乙在这次赛跑中的速度为 米/秒.
答案:(1) 100 (2) 甲 (3) 8
8.如图所示表示“龟兔赛跑”时路程与时间的关系,已知龟、兔上午8:00从同一地点出发,请你根据图中给出的信息,算出乌龟在 点追上兔子.
答案:10
9.为了增强居民的节水意识,从2007年1月1 日起,临汾城区水价执行“阶梯式”计费,每月应交水费(元)与用水量(吨)之间的函数关系如图所示.若某用户5月份交水费18.05元,则该用户该月用水 吨.
答案:9
10.初三体能素质测试中的一项是考查同学们的握力.2007年3月初,小杨和小李在摸底检测时,握力分别为30千克和34千克,他们不太满意,决定加强训练,争取在5月中旬测试时有较好成绩.小杨计划每周提高握力1.5千克,小李计划每周提高握力1千克.
(1) 分别写出两同学的握力(千克)与时间(周)之间的函数关系式;
(2) 请在下面的平面直角坐标系中,分别作出两个函数所在点的直线,并根据图象回答:第几周时,两人计划达到的握力一样?如果握力达到或超过45千克获得满分,那么按计划,谁先达到满分水平?
解:(1) 小杨:y1=30+1.5x;小李:y2=34+x.
(2) 图象如图. 由图象得, 当x=8时, 两人握力一样. 小杨先达到满分.
能力提升
11.弹簧的长度与所挂物体的质量的关系为一次函数,如图所示,由图可知不挂物体时弹簧的长度为…………………………………………………………………………………( )
A.7cm B.8cm C.9cm D.10cm
答案:D
12.如图,图象(折线)描述了某汽车在行驶过程中速度与时间的函数关系,下列说法中错误的是…………………………………………………………( )
A.第3分时汽车的速度是40千米/时 B.第12分时汽车的速度是0千米/时
C.从第3分到第6分,汽车行驶了120千米
D.从第9分到第12分,汽车的速度从60千米/时减少到0千米/时
答案:C
13.如图所示的函数图象反映的过程是:小明从家去书店,又去学校取封信后马上回家,其中x表示时间,y表示小明离他家的距离,则小明从学校回家的平均速度为 ___________千米∕小时.
答案:6
14.已知长方形的周长是20cm,一条边长的取值范围是2cm≤x≤4cm, 则它的邻边长的取值范围是 .
答案:6cm≤y≤8cm
15.暑假期间,王红随爸爸妈妈到一个著名森林风景区旅游,导游提醒大家上山要多带一件衣服,并介绍山区气温会随着海拔高度的增加而下降,沿途王红利用随身带的登山表(具有测定当前位置的海拔高度和气温等功能)测得以下的数据:
海拔高度(米)
300
400
500
600
700
…
气温(℃)
29.2
28.6
28.0
27.4
26.8
…
(1) 设海拔高度为(米),气温为(℃),根据上表提供的数据在下列直角坐点并连线.
(2) 观察(1)中所画出的图像,猜想与之间函数关系,求出所猜想标系中描的函数关系表达式.
(3) 如果王红到达山顶时,只告诉你山顶的气温为20.2℃,请计算此风景区山顶海拔高度大约是多少米?
解:(1) 如图.
(2) 由于(1)中四个点都在一盘棋直线上, 故y与x的函数关系为一次函数. 设y=kx+b, 则
, 解得.
∴函数关系式为y=-0.006x+31.
(3) 当y=20.2时, 20.2=-0.006x+31,
解得x=1800米.
16.为了鼓励小强做家务,小强每月的费用都是根据上月他的家务劳动时间所得奖励加上基本生活费从父母那里获取的.若设小强每月的家务劳动时间为x小时,该月可得(即下月他可获得)的总费用为y元,则y(元)和x(小时)之间的函数图像如图所示.
(1) 根据图像,请你写出小强每月的基本生活费;父母是如何奖励小强家务劳动的?
(2) 若小强5月份希望有250元费用,则小强4月份需做家务多少时间?
解:(1) 小强父母给小强的每月基本生活费为150元;
如果小强每月家务劳动时间不超过20小时,每小时获奖励2.5元;如果小强每月家务劳动时间超过20小时,那么20小时按每小时2.5元奖励,超过部分按每小时4元奖励.
(2) 设x≥20时y与x的函数关系式为y=kx+b,
则解得,∴.
由题意得,, 解得.
答:当小强4月份家务劳动32.5小时,5月份得到的费用为250元.
创新应用
17.一个水池有有2个速度相同的进水口,1个出水口,单开一个进水口每小时可进水10立方米,单开一个出水口每小时可出水20立方米. 某天0点到6点,该水池的蓄水量与时间的函数关系如图所示(至少打开一个进水口). 给出以下三个论断:(1)0点到3点只进水不出水;(2)3点到4点不进水只出水,(3)4点到6点不进水也不出水. 则错误的论断是______________(填序号).
解析:对于(1), 60÷3=20立方米 =(2×10)立方米, 即恰为2个进水管同时进水, 故(1)正确;对于(2), (60-50)÷1=10立方米=(20-10)立方米, 即为同时打开一个进水管和一个出水管, 故(2)错误;对于(3), 不一定, 可能同时打开2个进水管和1个出水管.
答案:(2), (3).
【要点预习】
利用图象取得函数解析式的基本步骤:
(1) 通过实验、测量获得数量足够多的 的对应值;
(2) 建立合适的直角坐标系, 在坐标系内以各对应值为坐标描点, 并用 法画出函数图象;
(3) 观察图象特征, 判定函数的 .
【课前热身】
1. 直线y=2x-1经过的点是……………………………………………………………( )
A. (2,1) B. (0,1) C. (2,0) D. (1,1)
答案:D
2. 给出下列函数:① ② ③;④.其中随着的增大而增大的是………………………………………………………………………………( )
A. ①② B. ③④ C. ①③ D. ②④
答案:C
3. 已知关于x的一次函数y=mx+1,如果y随x的增大而减小, 则m的取值范围是…( )
A. m>0 B. m<0 C.m≥0 D.m≤0
答案:B
4. 正比例函数的图象经过第一、三象限,则k的取值范围为 .
答案:k>3
【讲练互动】
【例1】如图所示,是某学校一电热淋浴器水箱的水量y(升)与供水时间x(分)的函数关系.
(1) 求y与x的函数关系式;
(2) 在(1)的条件下,求在30分钟时水箱有多少升水?
【解】(1) 由图可知y与x的函数关系是一次函数,设y=kx+b.
根据题意,得解得∴(10≤x≤50).
(2) 当x=30时,(升), ∴在30分钟时水箱有100升水.
【变式训练】
1.星期天,小王去朋友家借书,下图是他离家的距离(千米)与时间(分钟)的函数图象,根据图象信息,下列说法正确的是…………………………………( )
A.小王去时的速度大于回家的速度
B.小王在朋友家停留了10分钟
C.小王去时所花的时间少于回家所花的时间
D.小王去时走上坡路,回家时走下坡路
【答案】B
【例2】对于气温,有的地方用摄氏温度表示,有的地方用华氏温度表示,摄氏温度与华氏温度之间存在着某种函数关系,从温度计的刻度上可以看出,摄氏(℃)温度与华氏(°F)温度有如下对应关系:
x℃
…
-10
0
10
20
30
…
y°F
…
14
32
50
68
86
…
(1) 通过①描点连线;②猜测与之间的函数关系;③求解;④验证等几个步骤,试确定与之间的函数关系;
(2) 某天,南昌的最高气温是8℃,澳大利亚悉尼的最高气温是91°F,问这一天悉尼的最高气温比南昌的最高气温高多少摄氏度(结果保留整数).
【解】(1) 如图, 由于五个点都在同一直线上, 故函数可看作是一次函数, 设y=kx+b.
把(-10,14)和(0,32)代入, 得,解得.
∴y=1.8x+32.
(2) 当y=91时, 91=1.8x+32, 解得x≈33℃.
∴33-8=25℃, 即两地温度相差约25℃.
【变式训练】
2. 某校厨房有一太阳能热水器,其水箱的最大蓄水量为1200升.已知水箱的蓄水量y(升)与匀速注水时间x(分钟),在没有放水的情况下有如下关系:
x(分钟)
0
2
4
6
…
y(升)
0
80
160
240
…
(1) 根据上表中的数据,在上图的坐标系中描出相应的各点,顺次连结各点后,你发现这些点在哪一种图形上?猜一猜,符合这个图形的函数解析式;
(2) 请验证上表各点的坐标是否满足函数解析式,归纳你的结论,并写出自变量x的取值范围.
【解】(1)描点连结如图, 发现四个点在经过原点的一条直线上, 可以猜想函数解析式为y=kx.
(2) 把(2, 80)代入解析式, 得k=40, ∴y=40x(x≥0).
经验证, 其余各点均在y=40x上.
【同步测控】
基础自测
1. 在一次函数y=(2m+2)x+5中, y随x的增大而减小, 那么…………………………( )
A. m<-1 B.m>-1 C.m=1 D.m<1
答案:A
2. 某天早晨,小强从家出发,以v1的速度前往学校,途中在一饮食店吃早点,之后,以v2的速度向学校行进.已知v1>v2,下面的图象中表示小强从家到学校的时间t(分钟)与路程s(千米)之间的关系是……………………………………………………………………( )
答案:A
3.永州市内货摩(运货的摩托)的运输价格为:2千米内运费5元;路程超过2千米的,每超过1千米增加运费1元,那么运费y元与运输路程x千米的函数图象是…( )
答案:B
4.一辆汽车由韶关匀速驶往广州,下列图象中大致能反映汽车距离广州的路程S(千米)和行驶时间t(小时)的关系的是………………………………………………( )
答案:B
5.在某次实验中,测得两个变量m和v之间的4组对应数据如下表:
m
1
2
3
4
v
0.01
2.9
8.03
15.1
则m与v之间的关系最接近于下列各关系式中的……………………………………( )
A. v=2m-2 B. v=m 2-1 C.v=3m-3 D. v=m+1
答案:B
6.已知点A(–4,a),B(–2,b)都在直线(k为常数)上,则a与b的大小关系是a______b(填“<”“=”或“>”=).
答案:<
7. 假定甲、乙两人在一次赛跑中,路程s与时间t的关系如图所示,那么可以知道:(1)这是一次 米赛跑;(2)甲乙两人中先到达终点的是 ;(3)乙在这次赛跑中的速度为 米/秒.
答案:(1) 100 (2) 甲 (3) 8
8.如图所示表示“龟兔赛跑”时路程与时间的关系,已知龟、兔上午8:00从同一地点出发,请你根据图中给出的信息,算出乌龟在 点追上兔子.
答案:10
9.为了增强居民的节水意识,从2007年1月1 日起,临汾城区水价执行“阶梯式”计费,每月应交水费(元)与用水量(吨)之间的函数关系如图所示.若某用户5月份交水费18.05元,则该用户该月用水 吨.
答案:9
10.初三体能素质测试中的一项是考查同学们的握力.2007年3月初,小杨和小李在摸底检测时,握力分别为30千克和34千克,他们不太满意,决定加强训练,争取在5月中旬测试时有较好成绩.小杨计划每周提高握力1.5千克,小李计划每周提高握力1千克.
(1) 分别写出两同学的握力(千克)与时间(周)之间的函数关系式;
(2) 请在下面的平面直角坐标系中,分别作出两个函数所在点的直线,并根据图象回答:第几周时,两人计划达到的握力一样?如果握力达到或超过45千克获得满分,那么按计划,谁先达到满分水平?
解:(1) 小杨:y1=30+1.5x;小李:y2=34+x.
(2) 图象如图. 由图象得, 当x=8时, 两人握力一样. 小杨先达到满分.
能力提升
11.弹簧的长度与所挂物体的质量的关系为一次函数,如图所示,由图可知不挂物体时弹簧的长度为…………………………………………………………………………………( )
A.7cm B.8cm C.9cm D.10cm
答案:D
12.如图,图象(折线)描述了某汽车在行驶过程中速度与时间的函数关系,下列说法中错误的是…………………………………………………………( )
A.第3分时汽车的速度是40千米/时 B.第12分时汽车的速度是0千米/时
C.从第3分到第6分,汽车行驶了120千米
D.从第9分到第12分,汽车的速度从60千米/时减少到0千米/时
答案:C
13.如图所示的函数图象反映的过程是:小明从家去书店,又去学校取封信后马上回家,其中x表示时间,y表示小明离他家的距离,则小明从学校回家的平均速度为 ___________千米∕小时.
答案:6
14.已知长方形的周长是20cm,一条边长的取值范围是2cm≤x≤4cm, 则它的邻边长的取值范围是 .
答案:6cm≤y≤8cm
15.暑假期间,王红随爸爸妈妈到一个著名森林风景区旅游,导游提醒大家上山要多带一件衣服,并介绍山区气温会随着海拔高度的增加而下降,沿途王红利用随身带的登山表(具有测定当前位置的海拔高度和气温等功能)测得以下的数据:
海拔高度(米)
300
400
500
600
700
…
气温(℃)
29.2
28.6
28.0
27.4
26.8
…
(1) 设海拔高度为(米),气温为(℃),根据上表提供的数据在下列直角坐点并连线.
(2) 观察(1)中所画出的图像,猜想与之间函数关系,求出所猜想标系中描的函数关系表达式.
(3) 如果王红到达山顶时,只告诉你山顶的气温为20.2℃,请计算此风景区山顶海拔高度大约是多少米?
解:(1) 如图.
(2) 由于(1)中四个点都在一盘棋直线上, 故y与x的函数关系为一次函数. 设y=kx+b, 则
, 解得.
∴函数关系式为y=-0.006x+31.
(3) 当y=20.2时, 20.2=-0.006x+31,
解得x=1800米.
16.为了鼓励小强做家务,小强每月的费用都是根据上月他的家务劳动时间所得奖励加上基本生活费从父母那里获取的.若设小强每月的家务劳动时间为x小时,该月可得(即下月他可获得)的总费用为y元,则y(元)和x(小时)之间的函数图像如图所示.
(1) 根据图像,请你写出小强每月的基本生活费;父母是如何奖励小强家务劳动的?
(2) 若小强5月份希望有250元费用,则小强4月份需做家务多少时间?
解:(1) 小强父母给小强的每月基本生活费为150元;
如果小强每月家务劳动时间不超过20小时,每小时获奖励2.5元;如果小强每月家务劳动时间超过20小时,那么20小时按每小时2.5元奖励,超过部分按每小时4元奖励.
(2) 设x≥20时y与x的函数关系式为y=kx+b,
则解得,∴.
由题意得,, 解得.
答:当小强4月份家务劳动32.5小时,5月份得到的费用为250元.
创新应用
17.一个水池有有2个速度相同的进水口,1个出水口,单开一个进水口每小时可进水10立方米,单开一个出水口每小时可出水20立方米. 某天0点到6点,该水池的蓄水量与时间的函数关系如图所示(至少打开一个进水口). 给出以下三个论断:(1)0点到3点只进水不出水;(2)3点到4点不进水只出水,(3)4点到6点不进水也不出水. 则错误的论断是______________(填序号).
解析:对于(1), 60÷3=20立方米 =(2×10)立方米, 即恰为2个进水管同时进水, 故(1)正确;对于(2), (60-50)÷1=10立方米=(20-10)立方米, 即为同时打开一个进水管和一个出水管, 故(2)错误;对于(3), 不一定, 可能同时打开2个进水管和1个出水管.
答案:(2), (3).
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
