7.5一次函数的简单应用(2)(含答案解析)
文档属性
| 名称 | 7.5一次函数的简单应用(2)(含答案解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 316.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-30 00:00:00 | ||
图片预览


文档简介
7.5一次函数的简单应用(2)
【要点预习】
两个函数图象的交点坐标即为两个函数解析式联立的 的解.
【课前热身】
1. 函数y=kx+b(k、b为常数)的图象如图所示,则关于x的不等式kx+b>0的解集是………………………………………………( )
A. x>0 B. x<0 C. x<2 D. x>2
答案:C
2. 直线y=2x-4与x轴的交点坐标是 .
答案:(2, 0)
3.对于一次函数y=-x+5,当y>0时, x的取值范围是 .
答案:x<5
4. 已知直线y=2x-4和直线y=-3x+1交于一点(1,-2), 则方程组的解是 .
答案:
【讲练互动】
【例1】利用函数图象解二元一次方程组.
【分析】作出函数和的图象,它们的交点坐标就是所求.
【解】在同一坐标系内作函数和的图象, 它们的交点坐标是(1, 2).
∴二元一次方程组的解为.
【绿色通道】我们可以用方程组的解来确定函数图象的交点坐标;反之, 也可用画函数图象来解方程组.
【变式训练】
1. 请在同一直角坐标系内作出一次函数y=-2x+3与正比例函数y=2x的图象,直线y=-x+3与直线y=2x的交点坐标是 _______,方程组 的解是___ ___.
【答案】(1, 2)
【例2】甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图. 根据图象解决下列问题:
(1) 谁先出发?先出发多少时间?谁先到达终点?先到多少时间?
(2) 分别求出甲、乙两人的行驶速度;
(3) 在什么时间段内,两人均行驶在途中(不包括起点和终点)?在这一时间段内,请你根据下列情形,分别列出关于行驶时间x的方程或不等式(不化简,也不求解):① 甲在乙的前面;② 甲与乙相遇;③ 甲在乙后面.
【解】(1) 甲先出发,先出发10分钟,乙先到达终点,先到5分钟.
(2)甲、乙两人的行驶速度分别是12千米/小时,24千米/小时.
(3)10分钟到25分钟内,两人均行驶在途中.
①甲在乙的前面;②甲与乙相遇 ;③甲在乙后面 .
【变式训练】
2. 图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡. 使用这两种租书,租书金额(元)与租书时间(天)之间的关系如图所示.
(1) 分别写出用租书卡和会员卡租书的金额(元)与租书时间(天)之间的函数解析式;
(2) 两种租书方式每天租书的收费分别是多少元?
(3) 若两种租书卡的使用期限均为一年,则在这一年中如何选取这两种租书方式比较划算?
【解】(1)用租书卡租书:y=20+0.3x;用会员卡租书:y=0.5x.
(2) 用租书卡租书每天收费0.3元,用会员卡租书每天收费0.5元.
(3) 若两种租书卡的使用期限均为一年,则在这一年中应选取用租书卡租书划算.
【同步测控】
基础自测
1.如图,直线y=kx+b交坐标轴于A, B两点,则不等式kx+b>0的解是( )
A. x>-2 B. x>3 C. x<-2 D. x<3
答案:A
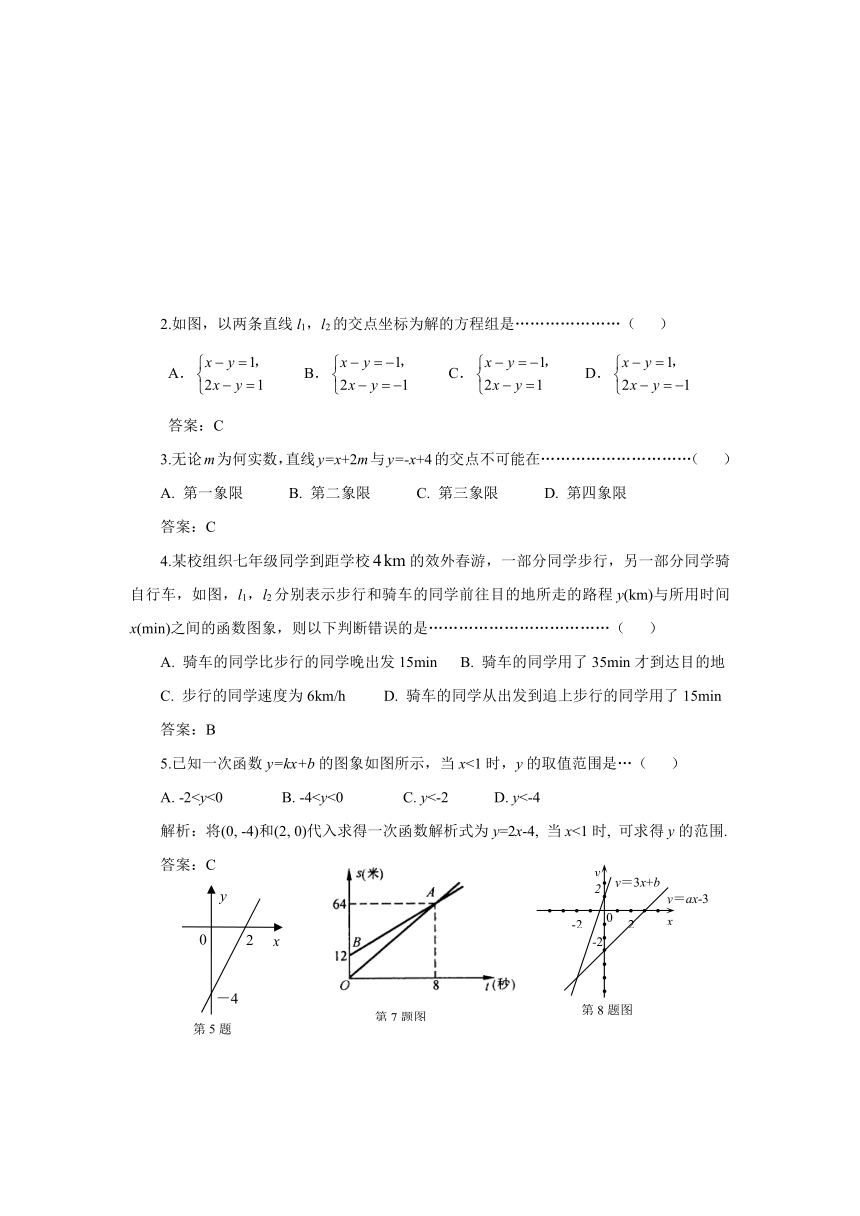
2.如图,以两条直线l1,l2的交点坐标为解的方程组是…………………( )
A. B. C. D.
答案:C
3.无论m为何实数,直线y=x+2m与y=-x+4的交点不可能在…………………………( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
答案:C
4.某校组织七年级同学到距学校的效外春游,一部分同学步行,另一部分同学骑自行车,如图,l1,l2分别表示步行和骑车的同学前往目的地所走的路程y(km)与所用时间x(min)之间的函数图象,则以下判断错误的是………………………………( )
A. 骑车的同学比步行的同学晚出发15min B. 骑车的同学用了35min才到达目的地
C. 步行的同学速度为6km/h D. 骑车的同学从出发到追上步行的同学用了15min
答案:B
5.已知一次函数y=kx+b的图象如图所示,当x<1时,y的取值范围是…( )
A. -2解析:将(0, -4)和(2, 0)代入求得一次函数解析式为y=2x-4, 当x<1时, 可求得y的范围.
答案:C
6. 已知函数y=-2x+8,当x 时,y>4;当x 时,y≤-2.
答案:<2 ≥5
7. 如图,OA、BA分别表示甲、乙两名学生运动的一次函数图象,图中s和t分别表示运动路程和时间,根据图象判断8秒前甲在乙的 .(填”前面”或”后面”).
答案:后面
8.如图,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式3x+b>ax-3的解集是_______________.
答案:x>-2
9. 已知一次函数y=3x+p和y=x+q的图象都经过点A(-2,0),且与y轴分别交于B、C两点,求△ABC的面积.
解:把x=-2, y=0代入, 得p=6, q=2, ∴y=3x+6, y=x+2, ∴B(0, 6), C(0, 2).
∴BC=6-2=4, OA=2, ∴S△ABC=BC·OA=4.
10. 2007年5月,第五届中国宜昌长江三峡国际龙舟拉力赛在黄陵庙揭开比赛帷幕.20日上午9时,参赛龙舟从黄陵庙同时出发.其中甲、乙两队在比赛时,路程y(千米)与时间x(小时)的函数关系如图所示.甲队在上午11时30分到达终点黄柏河港.
(1) 哪个队先到达终点?乙队何时追上甲队?
(2) 在比赛过程中,甲、乙两队何时相距最远?
解:(1)乙队先达到终点.
对于乙队,x=1时,y=16,∴y=16x,
对于甲队,出发1小时后,设y与x关系为y=kx+b,将x=1,y=20和x=2.5,y=35分别代入上式得:
解得:y=10x+10.
解方程组 得:x=.
即:出发1小时40分钟后(或者上午10点40分)乙队追上甲队.
(2) 1小时之内,两队相距最远距离是4千米,乙队追上甲队后,两队的距离是16x-(10x+10)=6x-10,当x为最大,即x=时,6x-10最大.
此时最大距离为6×-10=3.125<4,(也可以求出AD、CE的长度,比较其大小)
∴比赛过程中,甲、乙两队在出发后1小时(或者上午10时)相距最远.
能力提升
11.一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③当x<3时,y1< y2中,正确的个数是…………………………………………………………( )
A. 0 B. 1 C. 2 D. 3
答案:C
12.甲乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s(千米)和行驶时间t(时)之间的函数关系的图象,如图所示. 根据图中提供的信息,有下列说法:①他们都行驶了18千米;②甲车停留了0.5小时;③乙比甲晚出发了0.5小时;④相遇后甲的速度小于乙的速度;⑤甲、乙两人同时到达目的地. 其中符合图象描述的说法有……………………………………………………………( )
A. 2个 B. 3个 C. 4个 D. 5个
答案:C
13.如图,矩形ABCD中,AB=3,AD=4,动点P沿A→B→C→D的路线由A点运动到D点,则△APD的面积S是动点P运动的路径x的函数,这个函数的大致图象可能是……………………………………………………………( )
解析:当P在AB上, 即0答案:A
14. 若直线y=-x+a和直线y=x+b的交点坐标为(m, 8),则a+b=___________.
答案:16
15.直线y=kx+b经过点A(-2, 0)和y轴正半轴上的一点,如果△ABO(O为坐标原点)的面积为2,则b的值为 .
答案:2或-2
16.某化妆公司每月付给销售人员的工资有两种方案.
方案一:没有底薪,只拿销售提成;
方案二:底薪加销售提成.
设x(件)是销售商品的数量,y(元)是销售人员的月工资.如图所示,y1为方案一的函数图象,y2为方案二的函数图象.已知每件商品的销售提成方案二比方案一少7元.从图中信息解答如下问题(注:销售提成是指从销售每件商品得到的销售费中提取一定数量的费用):
(1) 求y1的函数解析式;
(2) 请问方案二中每月付给销售人员的底薪是多少元?
(3) 如果该公司销售人员小丽的月工资要超过1000元,那么小丽选用哪种方案最好,至少要销售商品多少件?
解:(1) 设y1的函数解析式为y=kx(x≥0).∵y1经过点(30,420),∴k=14.
∴y1的函数解析式为y=14x(x≥0).
(2) 设y2的函数解析式为y=ax+b(x≥0),它经过点(30,560),∴560=30a+b.
∵每件商品的销售提成方案二比方案一少7元,∴a=14-7=7.
∴560=30×7+b, ∴b=350,即方案二中每月付给销售人员的底薪为350元.
(3) 由(2),得y2的函数解析式为y=7x+350(x≥0).
解方程组,得. ∵1000>700, ∴小丽选择方案一最好.
由,得.∵x为正整数,∴x取最小整数72, 即至少要销售商品72件.
创新应用
17.如图9,M是边长为4的正方形AD边的中点,动点P自A点起,由A→B→C→D匀速运动,直线MP扫过正方形所形成的面积为y,点P运动的路程为x,请解答下列问题:
(1) 当x=1时,求y的值;
(2) 就下列各种情况,求y与x之间的函数关系式:
①0≤x≤4;②4(3) 在给出的直角坐标系(如图)中,画出(2)中函数的图像.
解:(1) 当x=1时, y=×2×1=1.
(2) ①0≤x≤4时, y=×2×x=x;
②4③8(3) 如图.
【要点预习】
两个函数图象的交点坐标即为两个函数解析式联立的 的解.
【课前热身】
1. 函数y=kx+b(k、b为常数)的图象如图所示,则关于x的不等式kx+b>0的解集是………………………………………………( )
A. x>0 B. x<0 C. x<2 D. x>2
答案:C
2. 直线y=2x-4与x轴的交点坐标是 .
答案:(2, 0)
3.对于一次函数y=-x+5,当y>0时, x的取值范围是 .
答案:x<5
4. 已知直线y=2x-4和直线y=-3x+1交于一点(1,-2), 则方程组的解是 .
答案:
【讲练互动】
【例1】利用函数图象解二元一次方程组.
【分析】作出函数和的图象,它们的交点坐标就是所求.
【解】在同一坐标系内作函数和的图象, 它们的交点坐标是(1, 2).
∴二元一次方程组的解为.
【绿色通道】我们可以用方程组的解来确定函数图象的交点坐标;反之, 也可用画函数图象来解方程组.
【变式训练】
1. 请在同一直角坐标系内作出一次函数y=-2x+3与正比例函数y=2x的图象,直线y=-x+3与直线y=2x的交点坐标是 _______,方程组 的解是___ ___.
【答案】(1, 2)
【例2】甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图. 根据图象解决下列问题:
(1) 谁先出发?先出发多少时间?谁先到达终点?先到多少时间?
(2) 分别求出甲、乙两人的行驶速度;
(3) 在什么时间段内,两人均行驶在途中(不包括起点和终点)?在这一时间段内,请你根据下列情形,分别列出关于行驶时间x的方程或不等式(不化简,也不求解):① 甲在乙的前面;② 甲与乙相遇;③ 甲在乙后面.
【解】(1) 甲先出发,先出发10分钟,乙先到达终点,先到5分钟.
(2)甲、乙两人的行驶速度分别是12千米/小时,24千米/小时.
(3)10分钟到25分钟内,两人均行驶在途中.
①甲在乙的前面;②甲与乙相遇 ;③甲在乙后面 .
【变式训练】
2. 图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡. 使用这两种租书,租书金额(元)与租书时间(天)之间的关系如图所示.
(1) 分别写出用租书卡和会员卡租书的金额(元)与租书时间(天)之间的函数解析式;
(2) 两种租书方式每天租书的收费分别是多少元?
(3) 若两种租书卡的使用期限均为一年,则在这一年中如何选取这两种租书方式比较划算?
【解】(1)用租书卡租书:y=20+0.3x;用会员卡租书:y=0.5x.
(2) 用租书卡租书每天收费0.3元,用会员卡租书每天收费0.5元.
(3) 若两种租书卡的使用期限均为一年,则在这一年中应选取用租书卡租书划算.
【同步测控】
基础自测
1.如图,直线y=kx+b交坐标轴于A, B两点,则不等式kx+b>0的解是( )
A. x>-2 B. x>3 C. x<-2 D. x<3
答案:A
2.如图,以两条直线l1,l2的交点坐标为解的方程组是…………………( )
A. B. C. D.
答案:C
3.无论m为何实数,直线y=x+2m与y=-x+4的交点不可能在…………………………( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
答案:C
4.某校组织七年级同学到距学校的效外春游,一部分同学步行,另一部分同学骑自行车,如图,l1,l2分别表示步行和骑车的同学前往目的地所走的路程y(km)与所用时间x(min)之间的函数图象,则以下判断错误的是………………………………( )
A. 骑车的同学比步行的同学晚出发15min B. 骑车的同学用了35min才到达目的地
C. 步行的同学速度为6km/h D. 骑车的同学从出发到追上步行的同学用了15min
答案:B
5.已知一次函数y=kx+b的图象如图所示,当x<1时,y的取值范围是…( )
A. -2
答案:C
6. 已知函数y=-2x+8,当x 时,y>4;当x 时,y≤-2.
答案:<2 ≥5
7. 如图,OA、BA分别表示甲、乙两名学生运动的一次函数图象,图中s和t分别表示运动路程和时间,根据图象判断8秒前甲在乙的 .(填”前面”或”后面”).
答案:后面
8.如图,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式3x+b>ax-3的解集是_______________.
答案:x>-2
9. 已知一次函数y=3x+p和y=x+q的图象都经过点A(-2,0),且与y轴分别交于B、C两点,求△ABC的面积.
解:把x=-2, y=0代入, 得p=6, q=2, ∴y=3x+6, y=x+2, ∴B(0, 6), C(0, 2).
∴BC=6-2=4, OA=2, ∴S△ABC=BC·OA=4.
10. 2007年5月,第五届中国宜昌长江三峡国际龙舟拉力赛在黄陵庙揭开比赛帷幕.20日上午9时,参赛龙舟从黄陵庙同时出发.其中甲、乙两队在比赛时,路程y(千米)与时间x(小时)的函数关系如图所示.甲队在上午11时30分到达终点黄柏河港.
(1) 哪个队先到达终点?乙队何时追上甲队?
(2) 在比赛过程中,甲、乙两队何时相距最远?
解:(1)乙队先达到终点.
对于乙队,x=1时,y=16,∴y=16x,
对于甲队,出发1小时后,设y与x关系为y=kx+b,将x=1,y=20和x=2.5,y=35分别代入上式得:
解得:y=10x+10.
解方程组 得:x=.
即:出发1小时40分钟后(或者上午10点40分)乙队追上甲队.
(2) 1小时之内,两队相距最远距离是4千米,乙队追上甲队后,两队的距离是16x-(10x+10)=6x-10,当x为最大,即x=时,6x-10最大.
此时最大距离为6×-10=3.125<4,(也可以求出AD、CE的长度,比较其大小)
∴比赛过程中,甲、乙两队在出发后1小时(或者上午10时)相距最远.
能力提升
11.一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③当x<3时,y1< y2中,正确的个数是…………………………………………………………( )
A. 0 B. 1 C. 2 D. 3
答案:C
12.甲乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s(千米)和行驶时间t(时)之间的函数关系的图象,如图所示. 根据图中提供的信息,有下列说法:①他们都行驶了18千米;②甲车停留了0.5小时;③乙比甲晚出发了0.5小时;④相遇后甲的速度小于乙的速度;⑤甲、乙两人同时到达目的地. 其中符合图象描述的说法有……………………………………………………………( )
A. 2个 B. 3个 C. 4个 D. 5个
答案:C
13.如图,矩形ABCD中,AB=3,AD=4,动点P沿A→B→C→D的路线由A点运动到D点,则△APD的面积S是动点P运动的路径x的函数,这个函数的大致图象可能是……………………………………………………………( )
解析:当P在AB上, 即0
14. 若直线y=-x+a和直线y=x+b的交点坐标为(m, 8),则a+b=___________.
答案:16
15.直线y=kx+b经过点A(-2, 0)和y轴正半轴上的一点,如果△ABO(O为坐标原点)的面积为2,则b的值为 .
答案:2或-2
16.某化妆公司每月付给销售人员的工资有两种方案.
方案一:没有底薪,只拿销售提成;
方案二:底薪加销售提成.
设x(件)是销售商品的数量,y(元)是销售人员的月工资.如图所示,y1为方案一的函数图象,y2为方案二的函数图象.已知每件商品的销售提成方案二比方案一少7元.从图中信息解答如下问题(注:销售提成是指从销售每件商品得到的销售费中提取一定数量的费用):
(1) 求y1的函数解析式;
(2) 请问方案二中每月付给销售人员的底薪是多少元?
(3) 如果该公司销售人员小丽的月工资要超过1000元,那么小丽选用哪种方案最好,至少要销售商品多少件?
解:(1) 设y1的函数解析式为y=kx(x≥0).∵y1经过点(30,420),∴k=14.
∴y1的函数解析式为y=14x(x≥0).
(2) 设y2的函数解析式为y=ax+b(x≥0),它经过点(30,560),∴560=30a+b.
∵每件商品的销售提成方案二比方案一少7元,∴a=14-7=7.
∴560=30×7+b, ∴b=350,即方案二中每月付给销售人员的底薪为350元.
(3) 由(2),得y2的函数解析式为y=7x+350(x≥0).
解方程组,得. ∵1000>700, ∴小丽选择方案一最好.
由,得.∵x为正整数,∴x取最小整数72, 即至少要销售商品72件.
创新应用
17.如图9,M是边长为4的正方形AD边的中点,动点P自A点起,由A→B→C→D匀速运动,直线MP扫过正方形所形成的面积为y,点P运动的路程为x,请解答下列问题:
(1) 当x=1时,求y的值;
(2) 就下列各种情况,求y与x之间的函数关系式:
①0≤x≤4;②4
解:(1) 当x=1时, y=×2×1=1.
(2) ①0≤x≤4时, y=×2×x=x;
②4
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
