二次函数的三种解析式

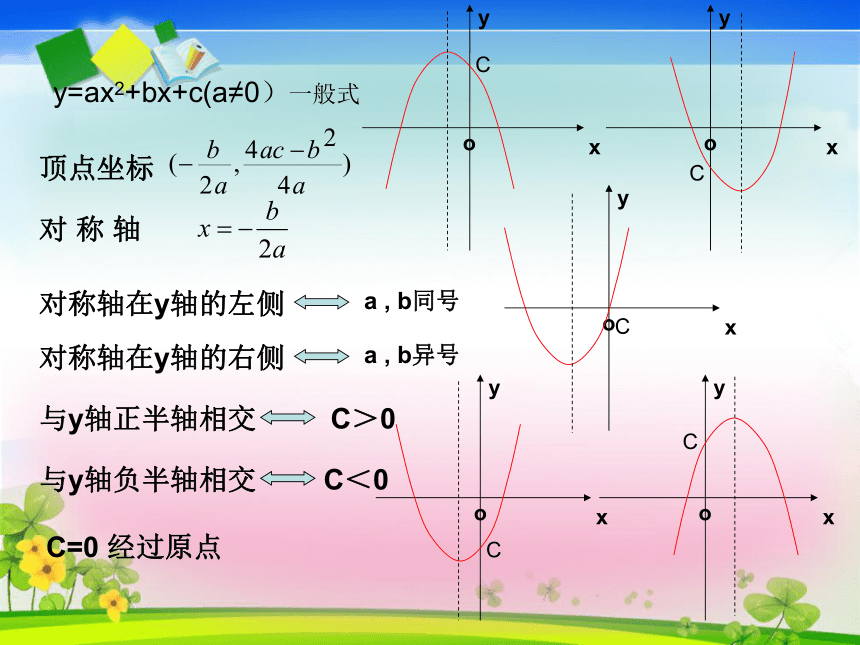
课件20张PPT。二次函数的三种解析式二次函数解析式常见的三种表示形式：(1)一般式(2)顶点式(3)交点式回味知识点：y=ax2+bx+c(a≠0）一般式a , b同号a , b异号C＞0C＜0C=0 经过原点顶点坐标对 称 轴与y轴正半轴相交
与y轴负半轴相交
对称轴在y轴的左侧
对称轴在y轴的右侧
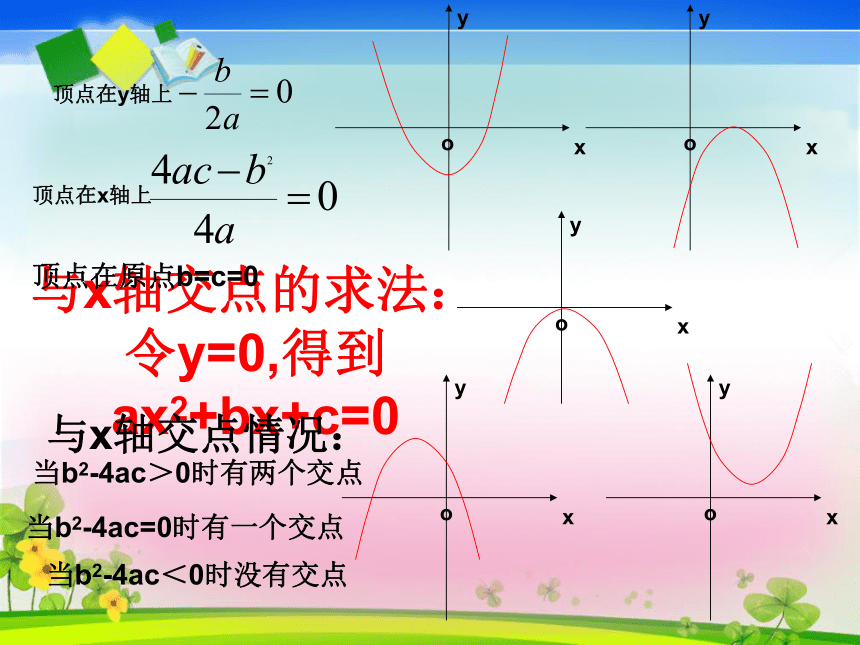
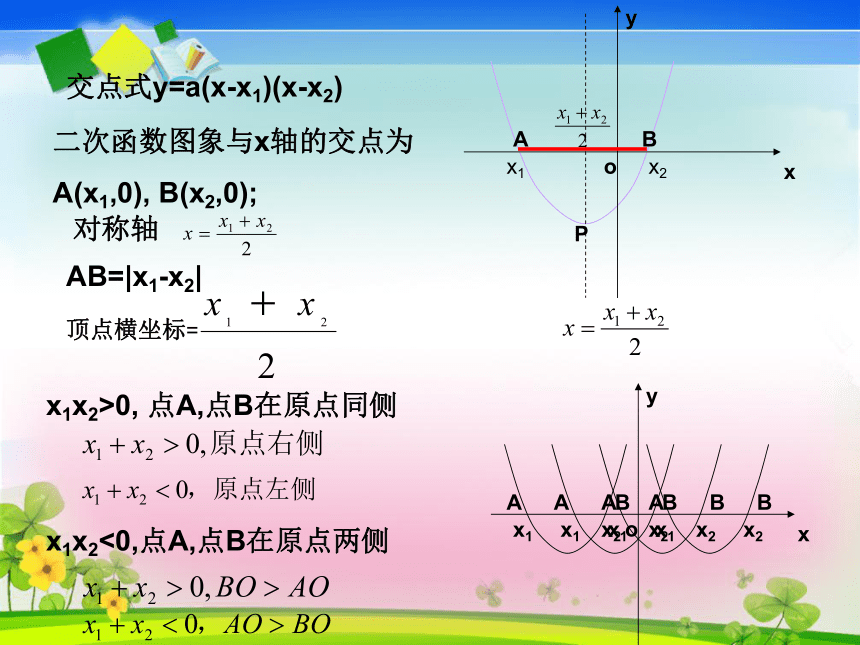
与x轴交点的求法：令y=0,得到ax2+bx+c=0与x轴交点情况：当b2-4ac＞0时有两个交点当b2-4ac=0时有一个交点当b2-4ac＜0时没有交点顶点在原点b=c=0与y轴交点的求法：令x=0,得到y=c 即（0，c）与y轴始终有一个交点（0，c）交点式y=a(x-x1)(x-x2)二次函数图象与x轴的交点为
A(x1,0), B(x2,0);AB=|x1-x2|PABx1x2>0, 点A,点B在原点同侧
x1x2<0,点A,点B在原点两侧
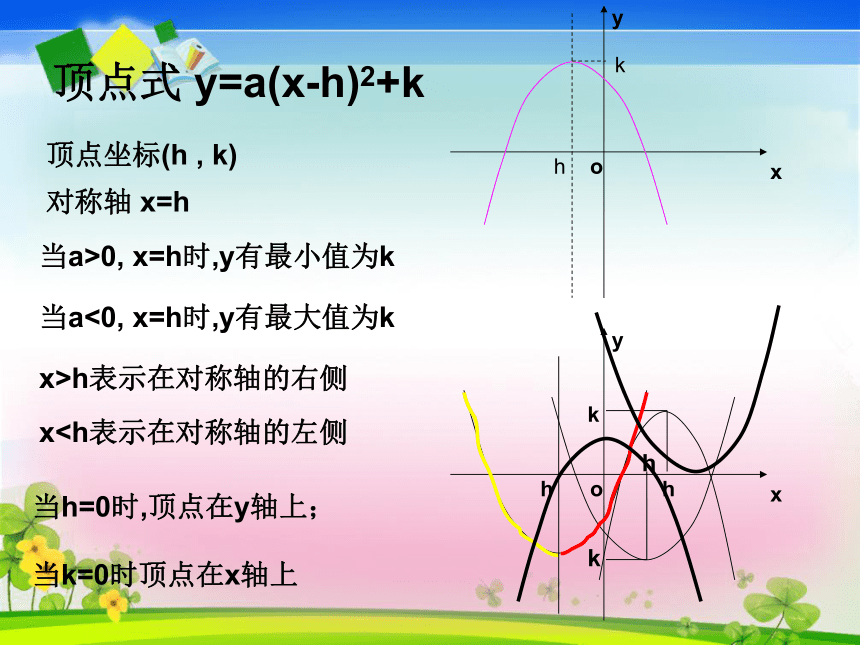
顶点式 y=a(x-h)2+k顶点坐标(h , k)对称轴 x=h当a>0, x=h时,y有最小值为kxx>h表示在对称轴的右侧
当h=0时,顶点在y轴上；
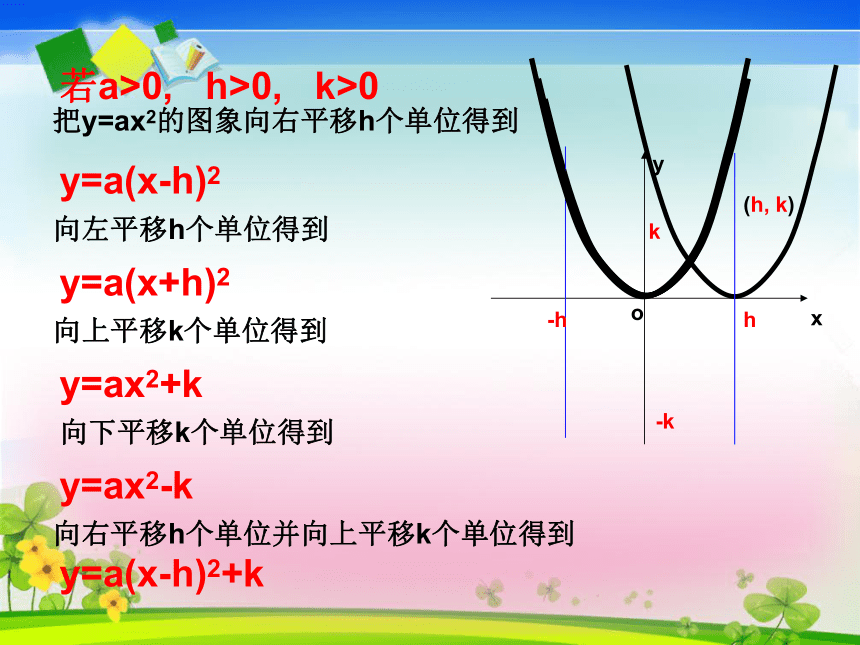
h-hk-k(h, k)若a>0, h>0, k>0把y=ax2的图象向右平移h个单位得到向左平移h个单位得到向上平移k个单位得到向下平移k个单位得到向右平移h个单位并向上平移k个单位得到y=a(x+h)2y=ax2+k
y=ax2-k
y=a(x-h)2+k
y=a(x-h)2
( 1 )图象过A(0，1) 、B（1，2）、C（2，-1）三点 一: 已知抛物线y=ax2+bx+c满足下列条件,求函数的解析式.（1）解：设抛物线的解析式为y=ax2+bx+c∵图象过A(0，1) 、B（1，2）、C（2，-1）三点
∴y= -2x2+3x+1解：∵A(1，0)，对称轴为x=2∴抛物线与x轴另一个交点C应为（3，0）∴设其解析式为y=a(x-1)(x-3)
∵B（0，-3）∴-3=a（0-1）（0-3）∴a= -1∴y= -(x-1)(x-3)
（2）图象经过A（1，0）、B（0，-3），且对称轴是直线x=21AB-3C3（3）图象顶点是（-2，3），且经过点（-1，5）解：∵图象顶点是（-2，3）∴设其解析式为y=a（x+2）2+3∵经过点（-1，5）∴5=a（-1+2）2+3∴a=2∴y=2（x+2）2+3（4）图象和x轴交于（-2，0）、（4，0）两点且顶点为（1，-9/2）解：由于题中告诉了图象与x轴的交点坐标，又告诉了顶点坐标，所以既可以用交点式又可以用顶点式来设其解析式设交点式为：y=a(x+2)(x-4)∴-9/2=a(1+2)(1-4)∵顶点为（1，-9/2）
∴a= -1/2∴y= -1/2(x+2)(x-4)
（5）图象顶点是M（1，16）且与x轴交于两点，已知两交点相距8个单位。
解： ∵顶点M坐标为（1，16），对称轴为x=1，又交点A、B关于直线x=1对称，AB=8∴A（-3，0）、B（5，0）∴此函数解析式可设为
y=a（x-1）2+16
或y=a（x+3）（x-5）116AB- 35二:求满足下列条件的抛物线的解析式(1)经过点A（2，4），B（-1，0）且在x轴上截得的线段长为2解： ∵B（-1，0）且在x轴上截得的线段长为2
∴抛物线与x轴的另一个交点坐标为C（-3，0）或C’（1，0）∴设抛物线的解析式为y=a（x- x1）（x- x2）①当抛物线经过A、B、C三点时，解析式为y=a（x+1）（x+3）又∵抛物线经过A（2，4）∴4=a（2+1）（2+3）②当抛物线经过A、B、C’ 三点时，解析式为y=a（x+1）（x-1）B-1- 31CC’(2)交x轴于A（x1，0），B（x2，0），顶点为P（1，-4），且x12+x22=10∵ x12+x22=10
∴x1= -1 ; x2=3∴ A（-1，0），B（3，0）∴抛物线的解析式为y=a（x+ 1）（x- 3）又∵抛物线的顶点为P （1，-4）∴-4=a（1+1）（1- 3）∴a=1∴y = （x+ 1）（x- 3）
1-4AB-13P课堂小结：1. 抛物线的三种解析式？3. 各种解析式对称轴、顶点坐标求法？2. 如何选择这三种解析式求抛物线的解析式？4. 二次函数的最值的求法？5. 抛物线的平移规律？6. 抛物线与x轴两交点距离的求法？过点（2，4），且当x=1时，y有最值6，求函数解析式。已知抛物线经过A，B，C三点，当时，其图象如图所示。 求抛物线的解析式。 如图，有一座抛物线型拱桥，桥下面在正常水位AB时宽为20米，水位上升3米就达到警戒线CD，这时水面宽度为10米.
(1)在如图的坐标系中求出此抛物线的表达式;
(2)若洪水到来时,水位以每小时0.2米的速度上升,从正常水位开始,再持续多长时间,会达到共拱顶?xyoCDAB