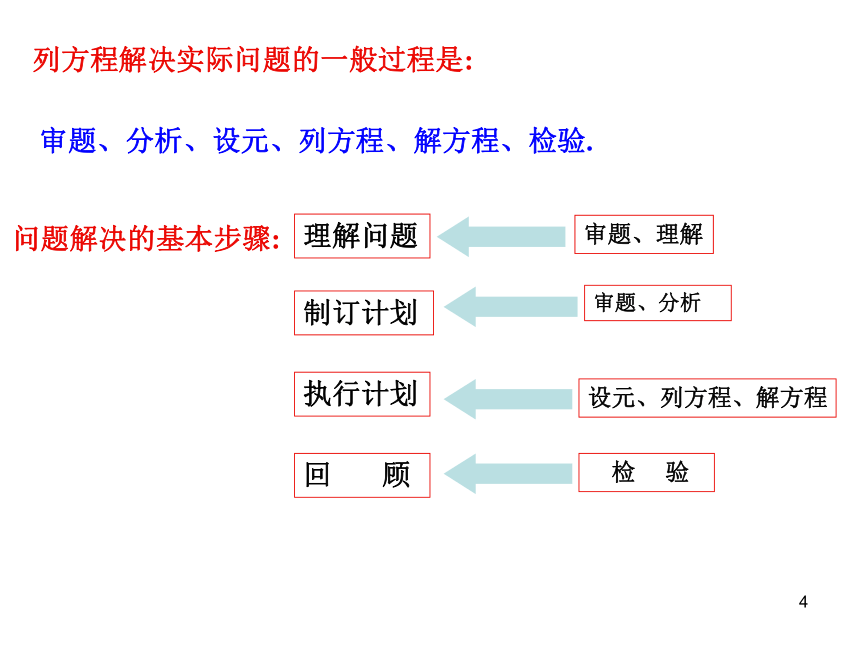
课题学习:问题解决的基本步骤
图片预览









文档简介
课件31张PPT。问题解决的基本步骤课题学习1以出门旅行为例
理解问题:旅行中应搞清出发地和目的地,两地之间的交通工具、时间、费用等等;
制订计划:通过对各种已知信息的分析,各种预想方案的比较,确定路线等实施方案;
执行计划:按制订的计划进行旅行的过程;
回顾:在完成旅行后回顾过程,获取有益的经验。11、理解问题:弄清问题的意思,以及问题中涉及的术语、词汇的含义,分清问题中的条件和结论等。2、制订计划:在理解问题的基础上,运用有关的数学知识和方法拟订出解决问题的思路和方法。3、执行计划:把已制订的计划具体地进行实施。4、回顾:对整个解题过程进行必要的检查和反思,也包括检验得到的答案是否适合方程和符合问题的实际,思考对原来的解法进行改进或尝试用不同的方法,进行举一反三等。在解决问题时,通常按四个步骤来进行:1列方程解决实际问题的一般过程是:审题、分析、设元、列方程、解方程、检验.1 在电话收费问题中隐含着许多有趣的数学问题。例题讲解1该问题涉及哪些量?这些量之间有何数量关系? 例1、电信公司推出两种移动电话计费方法:计费方法A是每月收月租费58元,通话时间不超过150分钟的部分免费,超过150分钟的按每分钟0.25元加收通话费。计费方法B是每月收月租费88元,通话时间不超过350分钟的部分免费,超过的部分按每分钟0.20元加收通话费。 用计费方法A的用户一个月累计通话360分所需话费,若改用计费方法B ,则可通话多少分钟?它比计费方法A通话时间多了还是少了?
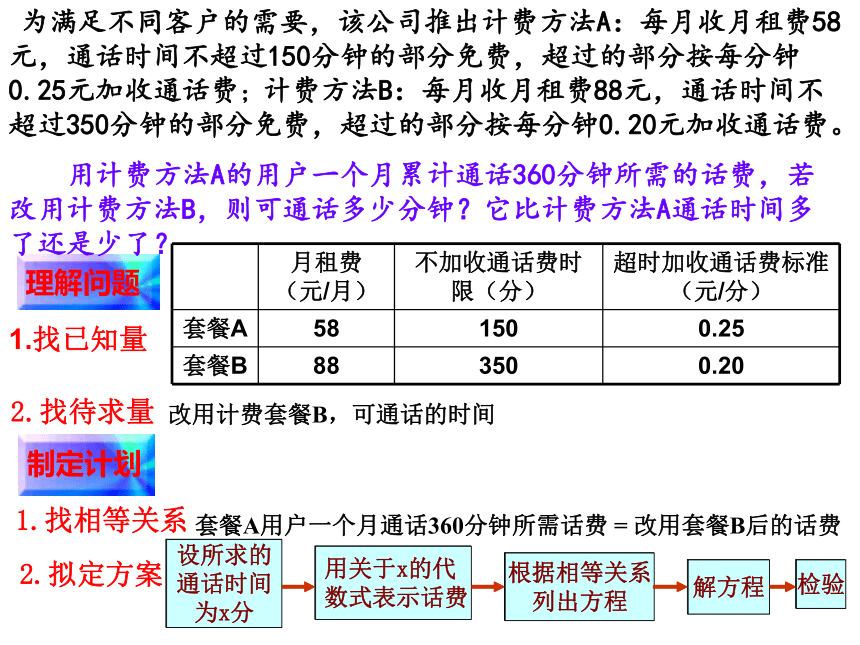
1 为满足不同客户的需要,该公司推出计费方法A:每月收月租费58元,通话时间不超过150分钟的部分免费,超过的部分按每分钟0.25元加收通话费;计费方法B:每月收月租费88元,通话时间不超过350分钟的部分免费,超过的部分按每分钟0.20元加收通话费。 用计费方法A的用户一个月累计通话360分钟所需的话费,若改用计费方法B,则可通话多少分钟?它比计费方法A通话时间多了还是少了?改用计费套餐B,可通话的时间套餐A用户一个月通话360分钟所需话费 = 改用套餐B后的话费1解:设所求的通话时间为x分,则有:答:用计费方法A的用户一个月累计通话360分
钟所需的话费,若改用计费方法B,则可多通话
102.5分钟?58+(360-150)×0.25=88+(x-350) ×0.20
解这个方程得:x=462.5462.5-360=102.53.执行计划14.回顾(1)把X =102.5代入方程,左边=右边。说明求解无误,结果也符合实际;(2)若某用户每月通话时间大于150分钟且不超过360分钟,有没有通话时间能令A、B两种套餐所需的话费相等?解:设x分钟A、B两种套餐所需的话费相等,则58+(x-150)×0.25=88解得:x=270答:通话270分钟能令A、B两种套餐所需的话费相等。1(3)若某用户每月通话时间超过360分钟,有没有通
话时间能令A、B两种套餐所需的话费相等?若通话
时间不超过150分钟呢?解:<1>超过360分钟时,设所求的通话时间为x分,则有:58+(x-150) ×0.25=88+(x-350) ×0.20
解得:x=-50 (不合题意,应舍去)<2>不超过150分钟时,A:58元 B:88元 ∴不可能4.回顾1商店出售茶壶和茶杯,茶壶每把24元,
茶杯每只5元.有两种优惠方法:
1.买一把茶壶送一只茶杯;
2.按原价打9折付款.
一位顾客买了5把茶壶和x只茶杯(x>5)
(1)计算两种方式的付款数y1和y2(用x的式子表示).
(2)购买多少只茶杯时,两种方法的付款数相同?
解(1) y1=24×5+5(x-5)=120+5x-25=95+5x
y2=24× 90% ×5+5×90%x=108+4.5x
(2)如果两种方法的付款数相同.
则 95+5x=108+4.5x
0.5x=13
x=26
答:购买26只茶杯时,两种方法的付款数相同。
练一练1例题2.胡华公司计划装运甲、乙、丙三种蔬菜到外地销售(每辆
汽车按规定满载),并且每一辆汽车只能装一种蔬菜,下表是每
辆汽车装运甲、乙、丙三种蔬菜的重量及利润,(1)若用8辆汽车装运乙、丙两种蔬菜11吨到A地销售,问装运
乙、丙两种蔬菜的汽车各多少辆?
(2)若用8辆汽车装运两种蔬菜11吨到A地销售,问装运哪两种
蔬菜利润最高?1解:(1)设用x辆汽车装运乙种蔬菜,则用(8-x)辆汽车装运丙种蔬菜,由题意可得,x+1.5(8-x)=11 , 解得,x=2(辆),
所以,运丙种蔬菜的汽车=8-2=6(辆);
答:装运乙、丙两种蔬菜的汽车各为2辆和6辆.解:(2)设用x辆汽车装运乙种蔬菜,则用(8-x)辆汽车装运丙种蔬菜,由题意可得,x+1.5(8-x)=11 , 解得,x=2(辆),所以,
运丙种蔬菜的汽车=8-2=6(辆);利润=2×2+6×1.5×4=40(百元)
即,装运乙、丙两种蔬菜获得利润是40百元.解:(2)设用x辆汽车装运乙种蔬菜,则用(8-x)辆汽车装运甲种蔬菜,由题意可得,x+2(8-x)=11 ,解得,x=5(辆),所以,运甲种蔬菜的汽车=8-5=3(辆);利润=5×2×1+3×2×5=40(百元)
即,装运乙、甲两种蔬菜获得利润是40百元.解:(2)设用x辆汽车装运甲种蔬菜,则用(8-x)辆汽车装运丙种蔬菜,由题意可得,2x+1.5(8-x)=11 ,解得,x=-2(辆),不符合题意舍去;
答:装运乙、丙或甲、乙两种蔬菜获得利润最高.1在100名学生中,会打羽毛球的有83人,会打乒乓球的有75人,这两项都不会的有10人,问这两项都会的有多少人?解:设两项都会的有x人,根据题意,得83+75 =100—10+x解这个方程,得 x =68答:两项都会的有68人。部分量+部分量=总量+重叠部分练一练1例题3.国庆节期间,胡华中学由4位教师和若干名学生旅游团,到
4A级旅游风景区---温州雁荡山旅游,甲旅行社的收费标准是:如
果4张全票,则其余的人按七折优惠;乙旅行社的收费标准是:5
人以上(含5人)可购买团体票,团体票的票价按原价八折优惠;这
两家旅行社的全票价都是300元/人.
(1)若有10位学生参加旅游团,问选择哪家旅行社更省钱?解:甲旅行社的收费是:乙旅行社的收费是:故此,选择甲旅行社更省钱。1例题3.国庆节期间,胡华中学由4位教师和若干名学生旅游团,到
4A级旅游风景区---温州雁荡山旅游,甲旅行社的收费标准是:如
果4张全票,则其余的人按七折优惠;乙旅行社的收费标准是:5
人以上(含5人)可购买团体票,团体票的票价按原价八折优惠;这
两家旅行社的全票价都是300元/人.
(2) 参加该旅游团的学生人数多少时,两家旅行社收费一样多?解:设参加该旅游团的学生人数为x时,两家旅行社收费一样多答:参加该旅游团的学生人数是8时,两家旅行社收费一样多.1例题3.国庆节期间,胡华中学由4位教师和若干名学生旅游团,到
4A级旅游风景区---温州雁荡山旅游,甲旅行社的收费标准是:如
果4张全票,则其余的人按七折优惠;乙旅行社的收费标准是:5
人以上(含5人)可购买团体票,团体票的票价按原价八折优惠;这
两家旅行社的全票价都是300元/人.
(3)请对参加该旅游团的学生人数进行讨论,选择哪家旅行社
更省钱?解:1练一练1.瑞安市煤气公司按以下规定收取每
月煤气费,所用煤气如果不超过60立
方米,按每立方米0.8元收费,如果超过60立方米,超过部分按每立方米1.2元收费,若胡华家10月份共
交煤气费66元,则胡华家10月份所用的煤气为多少立方米?解:设胡华家10月份所用的煤气为y立方米,由题意可得,
60×0.8+(y-60)×1.2=66, 解得 y=75m3,
答:胡华家10月份所用的煤气为75立方米.12.胡华齿轮厂有工人85人,平均每人每天可加工大齿轮16个或
小齿轮10个,已知两个大齿轮与三个小齿轮配成一套,问应怎
样安排工人才能使生产的产品刚好配套?解:设安排y人加工大齿轮,则加工小齿轮的人数为(85-y)人,答:安排生产大齿轮的工人为25人,生产小齿轮的工人60人,
才能使生产的产品刚好配套.1本节课你学到了什么?1总结升华同提高理解问题制订计划执行计划方程思想问题解决思想方法回顾★1、审清题意,分析各种量之间的关系,确定哪些量已知,哪些量未知。★2、注意书写规范,养成回顾、反思的好习惯。1【1】、复习、整理、巩固今天所学知识。一、必做题:1、作业本(2)第29页T1—T3;
2、参书第137页小结填空;
3.新同步练习第80--81页T1—T12
二、选做题:拓展探究题:参看幻灯片第23--31号。【2】、书面作业布置作业:11.如图,一个盛有水的圆柱形玻璃容器的内底面半径为 10cm,容器内水的高度为12cm.把一根半径为2cm的玻璃棒垂直插入水中,问 容器内水将升高多少cm?拓展探究题12.请你设计一道应用题,能用方程(1-25%)x=112.5求解,并检验你设计的题目是否符合生活实际。13 中国电信公司2009年调整后的201卡普通国内长话资费标准如下: 在21:00时拨打一个从温州到上海的电话,如果调整前的话费为3.40元,那么这个电话在调整后的话费是多少?理解问题(1)本题关系通话时间、收费标准和话费三个量.它们之间的关系是: 通话时间×收费标准=话费(2)已知量:(3)待求量:这个电话在调整后的话费.调整前和调整后的资费标准.在21:00拨打一个电话调整前的话费为3.40元.制订计划对于同一个电话,不论按调整前或调整后资费标准计费,通话时间不变,可用列方程求解. 根据等量关系列方程解方程检验执行计划回顾1解:这个电话在在调整后的话费是x元。根据题意,得在21:00时拨打一个从杭州到上海的电话,如果调整前的话费为3.40元,那么这个电话在调整后的话费是多少?0.030.04x3.4=解:这个方程,得x=2.55答:这个电话在在调整后的话费是2.55元调整前的通话时间=调整后的通话时间1解:这个电话在在调整后的话费是x元。根据题意,得在21:00时拨打一个从杭州到上海的电话,如果调整前的话费为3.4元,那么这个电话在调整后的话费是多少?0.030.04x20=解:这个方程,得x=15答:这个电话在在调整后的话费是15元调整前的通话时间=调整后的通话时间20元1在21:00时拨打一个从杭州到上海的电话,如果调整前的话费为20元,那么这个电话在调整后的话费是多少?调整前的通话时间=调整后的通话时间30元解:∵调整前在21:00—22:00打电话的话费为60×0.4=24<30∴有一部分时间是在22:00以后通话∴在22:00以后通话时间为:30-240.3=20∴此次通话时间为:60+20=80(分)这个电话在调整后的话费是80×0.3=241一个从19:50分开始打的电话,在调整后话费节省了1.8元,那么这个电话在何时通话结束?调整后的话费是多少?解:设通话时间为x分,根据题意,得∵在19:50—20:00时调整后比调整前少用:10×(0.6-0.3)=3元>1.8元∴这个电话的通话时间小于10分钟0.6x-0.3x=1.8解这个方程,得x=6∴这个电话在19:56通话结束.调整后的话费是0.3×6=1.8元1一个从19:50分开始打的电话,在调整后话费节省了1.8元,那么这个电话在何时通话结束?调整后的话费是多少?10元解:设通话时间为x分,根据题意,得∵在19:50—20:00时调整后比调整前少用:10×0.3=3元<10元∴这个电话的通话时间大于10分钟10×0.6+0.4(x-10)-0.3x=10解这个方程,得x=80∴这个电话在21:10通话结束.调整后的话费是0.3×80=24元1一个从19:50分开始打的电话,在调整后话费节省了1.8元,那么这个电话在何时通话结束?调整后的话费是多少?30元解:节省30元是不可能的∵只有在19:50—22:00的通话才会产生节省话费为:10×(0.6-0.3)+120×(0.4-0.3)=15元1
理解问题:旅行中应搞清出发地和目的地,两地之间的交通工具、时间、费用等等;
制订计划:通过对各种已知信息的分析,各种预想方案的比较,确定路线等实施方案;
执行计划:按制订的计划进行旅行的过程;
回顾:在完成旅行后回顾过程,获取有益的经验。11、理解问题:弄清问题的意思,以及问题中涉及的术语、词汇的含义,分清问题中的条件和结论等。2、制订计划:在理解问题的基础上,运用有关的数学知识和方法拟订出解决问题的思路和方法。3、执行计划:把已制订的计划具体地进行实施。4、回顾:对整个解题过程进行必要的检查和反思,也包括检验得到的答案是否适合方程和符合问题的实际,思考对原来的解法进行改进或尝试用不同的方法,进行举一反三等。在解决问题时,通常按四个步骤来进行:1列方程解决实际问题的一般过程是:审题、分析、设元、列方程、解方程、检验.1 在电话收费问题中隐含着许多有趣的数学问题。例题讲解1该问题涉及哪些量?这些量之间有何数量关系? 例1、电信公司推出两种移动电话计费方法:计费方法A是每月收月租费58元,通话时间不超过150分钟的部分免费,超过150分钟的按每分钟0.25元加收通话费。计费方法B是每月收月租费88元,通话时间不超过350分钟的部分免费,超过的部分按每分钟0.20元加收通话费。 用计费方法A的用户一个月累计通话360分所需话费,若改用计费方法B ,则可通话多少分钟?它比计费方法A通话时间多了还是少了?
1 为满足不同客户的需要,该公司推出计费方法A:每月收月租费58元,通话时间不超过150分钟的部分免费,超过的部分按每分钟0.25元加收通话费;计费方法B:每月收月租费88元,通话时间不超过350分钟的部分免费,超过的部分按每分钟0.20元加收通话费。 用计费方法A的用户一个月累计通话360分钟所需的话费,若改用计费方法B,则可通话多少分钟?它比计费方法A通话时间多了还是少了?改用计费套餐B,可通话的时间套餐A用户一个月通话360分钟所需话费 = 改用套餐B后的话费1解:设所求的通话时间为x分,则有:答:用计费方法A的用户一个月累计通话360分
钟所需的话费,若改用计费方法B,则可多通话
102.5分钟?58+(360-150)×0.25=88+(x-350) ×0.20
解这个方程得:x=462.5462.5-360=102.53.执行计划14.回顾(1)把X =102.5代入方程,左边=右边。说明求解无误,结果也符合实际;(2)若某用户每月通话时间大于150分钟且不超过360分钟,有没有通话时间能令A、B两种套餐所需的话费相等?解:设x分钟A、B两种套餐所需的话费相等,则58+(x-150)×0.25=88解得:x=270答:通话270分钟能令A、B两种套餐所需的话费相等。1(3)若某用户每月通话时间超过360分钟,有没有通
话时间能令A、B两种套餐所需的话费相等?若通话
时间不超过150分钟呢?解:<1>超过360分钟时,设所求的通话时间为x分,则有:58+(x-150) ×0.25=88+(x-350) ×0.20
解得:x=-50 (不合题意,应舍去)<2>不超过150分钟时,A:58元 B:88元 ∴不可能4.回顾1商店出售茶壶和茶杯,茶壶每把24元,
茶杯每只5元.有两种优惠方法:
1.买一把茶壶送一只茶杯;
2.按原价打9折付款.
一位顾客买了5把茶壶和x只茶杯(x>5)
(1)计算两种方式的付款数y1和y2(用x的式子表示).
(2)购买多少只茶杯时,两种方法的付款数相同?
解(1) y1=24×5+5(x-5)=120+5x-25=95+5x
y2=24× 90% ×5+5×90%x=108+4.5x
(2)如果两种方法的付款数相同.
则 95+5x=108+4.5x
0.5x=13
x=26
答:购买26只茶杯时,两种方法的付款数相同。
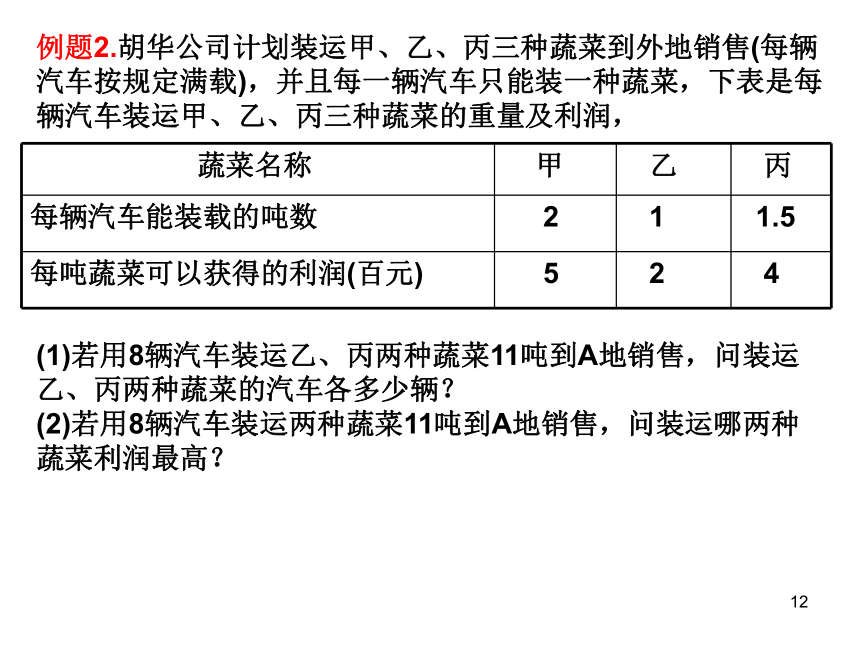
练一练1例题2.胡华公司计划装运甲、乙、丙三种蔬菜到外地销售(每辆
汽车按规定满载),并且每一辆汽车只能装一种蔬菜,下表是每
辆汽车装运甲、乙、丙三种蔬菜的重量及利润,(1)若用8辆汽车装运乙、丙两种蔬菜11吨到A地销售,问装运
乙、丙两种蔬菜的汽车各多少辆?
(2)若用8辆汽车装运两种蔬菜11吨到A地销售,问装运哪两种
蔬菜利润最高?1解:(1)设用x辆汽车装运乙种蔬菜,则用(8-x)辆汽车装运丙种蔬菜,由题意可得,x+1.5(8-x)=11 , 解得,x=2(辆),
所以,运丙种蔬菜的汽车=8-2=6(辆);
答:装运乙、丙两种蔬菜的汽车各为2辆和6辆.解:(2)设用x辆汽车装运乙种蔬菜,则用(8-x)辆汽车装运丙种蔬菜,由题意可得,x+1.5(8-x)=11 , 解得,x=2(辆),所以,
运丙种蔬菜的汽车=8-2=6(辆);利润=2×2+6×1.5×4=40(百元)
即,装运乙、丙两种蔬菜获得利润是40百元.解:(2)设用x辆汽车装运乙种蔬菜,则用(8-x)辆汽车装运甲种蔬菜,由题意可得,x+2(8-x)=11 ,解得,x=5(辆),所以,运甲种蔬菜的汽车=8-5=3(辆);利润=5×2×1+3×2×5=40(百元)
即,装运乙、甲两种蔬菜获得利润是40百元.解:(2)设用x辆汽车装运甲种蔬菜,则用(8-x)辆汽车装运丙种蔬菜,由题意可得,2x+1.5(8-x)=11 ,解得,x=-2(辆),不符合题意舍去;
答:装运乙、丙或甲、乙两种蔬菜获得利润最高.1在100名学生中,会打羽毛球的有83人,会打乒乓球的有75人,这两项都不会的有10人,问这两项都会的有多少人?解:设两项都会的有x人,根据题意,得83+75 =100—10+x解这个方程,得 x =68答:两项都会的有68人。部分量+部分量=总量+重叠部分练一练1例题3.国庆节期间,胡华中学由4位教师和若干名学生旅游团,到
4A级旅游风景区---温州雁荡山旅游,甲旅行社的收费标准是:如
果4张全票,则其余的人按七折优惠;乙旅行社的收费标准是:5
人以上(含5人)可购买团体票,团体票的票价按原价八折优惠;这
两家旅行社的全票价都是300元/人.
(1)若有10位学生参加旅游团,问选择哪家旅行社更省钱?解:甲旅行社的收费是:乙旅行社的收费是:故此,选择甲旅行社更省钱。1例题3.国庆节期间,胡华中学由4位教师和若干名学生旅游团,到
4A级旅游风景区---温州雁荡山旅游,甲旅行社的收费标准是:如
果4张全票,则其余的人按七折优惠;乙旅行社的收费标准是:5
人以上(含5人)可购买团体票,团体票的票价按原价八折优惠;这
两家旅行社的全票价都是300元/人.
(2) 参加该旅游团的学生人数多少时,两家旅行社收费一样多?解:设参加该旅游团的学生人数为x时,两家旅行社收费一样多答:参加该旅游团的学生人数是8时,两家旅行社收费一样多.1例题3.国庆节期间,胡华中学由4位教师和若干名学生旅游团,到
4A级旅游风景区---温州雁荡山旅游,甲旅行社的收费标准是:如
果4张全票,则其余的人按七折优惠;乙旅行社的收费标准是:5
人以上(含5人)可购买团体票,团体票的票价按原价八折优惠;这
两家旅行社的全票价都是300元/人.
(3)请对参加该旅游团的学生人数进行讨论,选择哪家旅行社
更省钱?解:1练一练1.瑞安市煤气公司按以下规定收取每
月煤气费,所用煤气如果不超过60立
方米,按每立方米0.8元收费,如果超过60立方米,超过部分按每立方米1.2元收费,若胡华家10月份共
交煤气费66元,则胡华家10月份所用的煤气为多少立方米?解:设胡华家10月份所用的煤气为y立方米,由题意可得,
60×0.8+(y-60)×1.2=66, 解得 y=75m3,
答:胡华家10月份所用的煤气为75立方米.12.胡华齿轮厂有工人85人,平均每人每天可加工大齿轮16个或
小齿轮10个,已知两个大齿轮与三个小齿轮配成一套,问应怎
样安排工人才能使生产的产品刚好配套?解:设安排y人加工大齿轮,则加工小齿轮的人数为(85-y)人,答:安排生产大齿轮的工人为25人,生产小齿轮的工人60人,
才能使生产的产品刚好配套.1本节课你学到了什么?1总结升华同提高理解问题制订计划执行计划方程思想问题解决思想方法回顾★1、审清题意,分析各种量之间的关系,确定哪些量已知,哪些量未知。★2、注意书写规范,养成回顾、反思的好习惯。1【1】、复习、整理、巩固今天所学知识。一、必做题:1、作业本(2)第29页T1—T3;
2、参书第137页小结填空;
3.新同步练习第80--81页T1—T12
二、选做题:拓展探究题:参看幻灯片第23--31号。【2】、书面作业布置作业:11.如图,一个盛有水的圆柱形玻璃容器的内底面半径为 10cm,容器内水的高度为12cm.把一根半径为2cm的玻璃棒垂直插入水中,问 容器内水将升高多少cm?拓展探究题12.请你设计一道应用题,能用方程(1-25%)x=112.5求解,并检验你设计的题目是否符合生活实际。13 中国电信公司2009年调整后的201卡普通国内长话资费标准如下: 在21:00时拨打一个从温州到上海的电话,如果调整前的话费为3.40元,那么这个电话在调整后的话费是多少?理解问题(1)本题关系通话时间、收费标准和话费三个量.它们之间的关系是: 通话时间×收费标准=话费(2)已知量:(3)待求量:这个电话在调整后的话费.调整前和调整后的资费标准.在21:00拨打一个电话调整前的话费为3.40元.制订计划对于同一个电话,不论按调整前或调整后资费标准计费,通话时间不变,可用列方程求解. 根据等量关系列方程解方程检验执行计划回顾1解:这个电话在在调整后的话费是x元。根据题意,得在21:00时拨打一个从杭州到上海的电话,如果调整前的话费为3.40元,那么这个电话在调整后的话费是多少?0.030.04x3.4=解:这个方程,得x=2.55答:这个电话在在调整后的话费是2.55元调整前的通话时间=调整后的通话时间1解:这个电话在在调整后的话费是x元。根据题意,得在21:00时拨打一个从杭州到上海的电话,如果调整前的话费为3.4元,那么这个电话在调整后的话费是多少?0.030.04x20=解:这个方程,得x=15答:这个电话在在调整后的话费是15元调整前的通话时间=调整后的通话时间20元1在21:00时拨打一个从杭州到上海的电话,如果调整前的话费为20元,那么这个电话在调整后的话费是多少?调整前的通话时间=调整后的通话时间30元解:∵调整前在21:00—22:00打电话的话费为60×0.4=24<30∴有一部分时间是在22:00以后通话∴在22:00以后通话时间为:30-240.3=20∴此次通话时间为:60+20=80(分)这个电话在调整后的话费是80×0.3=241一个从19:50分开始打的电话,在调整后话费节省了1.8元,那么这个电话在何时通话结束?调整后的话费是多少?解:设通话时间为x分,根据题意,得∵在19:50—20:00时调整后比调整前少用:10×(0.6-0.3)=3元>1.8元∴这个电话的通话时间小于10分钟0.6x-0.3x=1.8解这个方程,得x=6∴这个电话在19:56通话结束.调整后的话费是0.3×6=1.8元1一个从19:50分开始打的电话,在调整后话费节省了1.8元,那么这个电话在何时通话结束?调整后的话费是多少?10元解:设通话时间为x分,根据题意,得∵在19:50—20:00时调整后比调整前少用:10×0.3=3元<10元∴这个电话的通话时间大于10分钟10×0.6+0.4(x-10)-0.3x=10解这个方程,得x=80∴这个电话在21:10通话结束.调整后的话费是0.3×80=24元1一个从19:50分开始打的电话,在调整后话费节省了1.8元,那么这个电话在何时通话结束?调整后的话费是多少?30元解:节省30元是不可能的∵只有在19:50—22:00的通话才会产生节省话费为:10×(0.6-0.3)+120×(0.4-0.3)=15元1
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
