二次函数专项练习――图象(无答案)

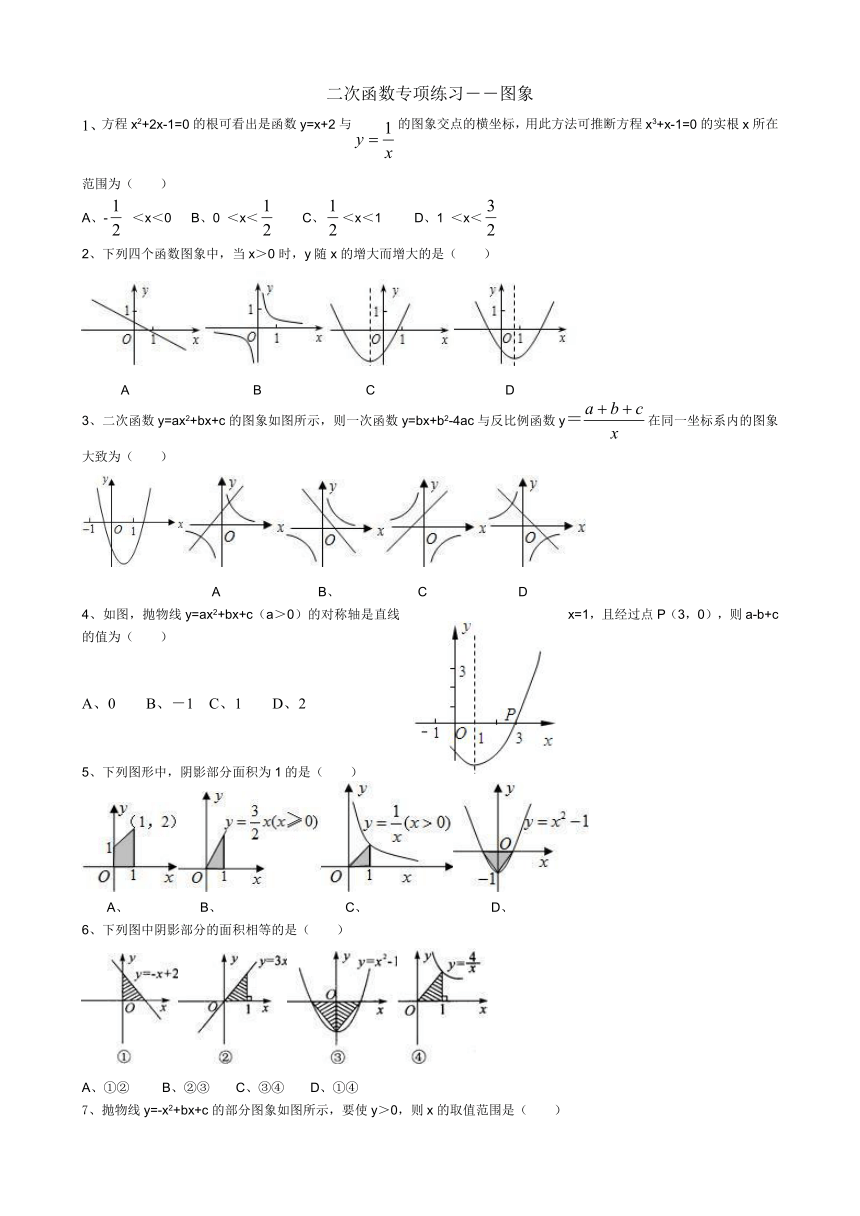
二次函数专项练习――图象
1、方程x2+2x-1=0的根可看出是函数y=x+2与的图象交点的横坐标，用此方法可推断方程x3+x-1=0的实根x所在范围为（　　）
A、- ＜x＜0 B、0 ＜x＜ C、＜x＜1 D、1 ＜x＜
2、下列四个函数图象中，当x＞0时，y随x的增大而增大的是（　　）
A B C D
3、二次函数y=ax2+bx+c的图象如图所示，则一次函数y=bx+b2-4ac与反比例函数y在同一坐标系内的图象大致为（　　）
A B、 C D
4、如图，抛物线y=ax2+bx+c（a＞0）的对称轴是直线x=1，且经过点P（3，0），则a-b+c的值为（　　）
A、0 B、－1 C、1 D、2
5、下列图形中，阴影部分面积为1的是（　　）
A、 B、 C、 D、
6、下列图中阴影部分的面积相等的是（　　）
A、①② B、②③ C、③④ D、①④
7、抛物线y=-x2+bx+c的部分图象如图所示，要使y＞0，则x的取值范围是（　　）

A、-4＜x＜1
B、-3＜x＜1
C、x＜-4或x＞1
D、x＜-3或x＞1
8、?二次函数y=ax2+bx+c图象上部分的对应值如下表，则y＞0时，x的取值范围是（　　）
A、-1＜x＜2 B、x＞2或x＜-1 C、-1≤x≤2 D、x≥2或x≤-1
9、在同一坐标系中，函数y=ax2+b与y=bx2+ax的图象只可能是（　　）
A、 B、 c、 D
10、?用min{a，b}表示a，b两数中的最小数，若函数y=min{x2+1，1-x2}，则y的图象为（　　）
A B C D
11、方程正数解的个数为（ ）
A、3 B、2 C、1 D、0
12、如图，边长为2的正方形ABCD的中心在直角坐标系的原点O，AD∥x轴，以O为顶点且过A、D两点的抛物线与以O为顶点且过B、C两点的抛物线将正方形分割成几部分．则图中阴影部分的面积是（ ）
13、如图，已知函数y=－3/x与y=ax2+bx（a＞0，b＞0）的图象交于点P．点P的纵坐标为1．则关于x的方程ax2+bx+ 3/x=0的解为( )
14、?如图所示四个二次函数的图象中，分别对应的是①y=ax2；②y=bx2；③y=cx2；④y=dx2．则a、b、c、d的大小关系为（　　　　）
15、?已知二次函数y=（x-3a）2-（3a+2）（a为常数），当a取不同的值时，其图象构成一个“抛物线系”．图中分别是当a=-1，a=- 13，a=1时二次函数的图象．则它们的顶点所满足的函数关系式为（　　　　　　　）
16、如图，两条抛物线y1=- ，y2= 与分别经过点（-2，0），（2，0）且平行于y轴的两条平行线围成的阴影部分的面积为（　　）
17、如图，记抛物线y=-x2+1的图象与x正半轴的交点为A，将线段OA分成n等份，设分点分别为P1，P2，…Pn-1，过每个分点作x轴的垂线，分别与抛物线交于点Q1，Q2，…，Qn-1，再记直角三角形OP1Q1，P1P2Q2，…，Pn-2Pn-1Qn-1的面积分别为S1，S2，…，这样就有S1= ，S2= ，…；记W=S1+S2+…+Sn-1，当n越来越大时，你猜想W最接近的常数是（　　）A、A、 2/3 B、 1/2 C、 1/ 3 D、 1/4
18、抛物线y=ax2与直线x=1，x=2，y=1，y=2围成的正方形有公共点，则实数a的取值范围是（　　）
A、 1/4≤a≤1 B、 1/2≤a≤2 C、 1/2≤a≤1 D、 1/4≤a≤2