特殊平行四边形（培优）

初二数学培优训练：特殊平行四边形2
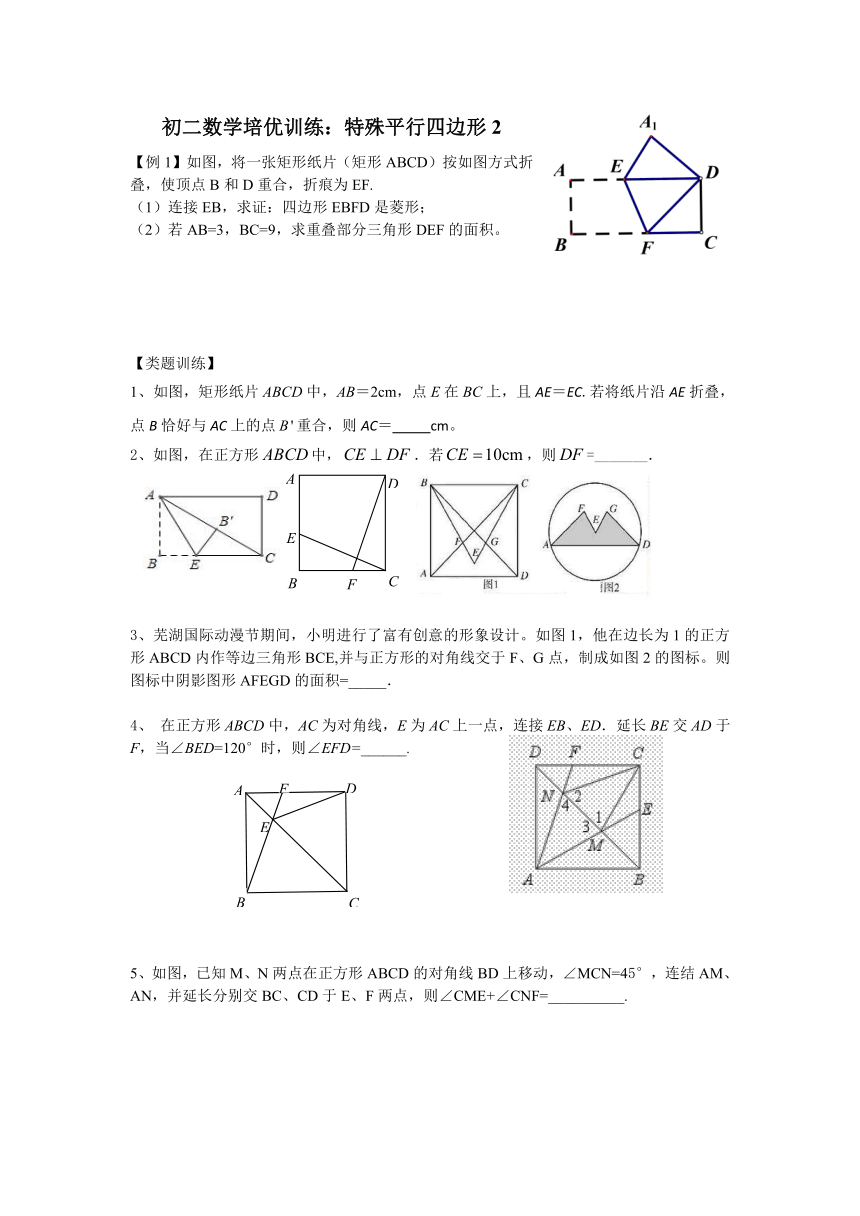
【例1】如图，将一张矩形纸片（矩形ABCD）按如图方式折叠，使顶点B和D重合，折痕为EF.
（1）连接EB，求证：四边形EBFD是菱形；
（2）若AB=3，BC=9，求重叠部分三角形DEF的面积。
【类题训练】
1、如图，矩形纸片ABCD中，AB＝2cm，点E在BC上，且AE＝EC.若将纸片沿AE折叠，点B恰好与AC上的点重合，则AC＝ cm。
2、如图，在正方形中，．若，则=_______．
3、芜湖国际动漫节期间，小明进行了富有创意的形象设计。如图1，他在边长为1的正方形ABCD内作等边三角形BCE,并与正方形的对角线交于F、G点，制成如图2的图标。则图标中阴影图形AFEGD的面积=_____．
4、 在正方形ABCD中，AC为对角线，E为AC上一点，连接EB、ED．延长BE交AD于F，当∠BED=120°时，则∠EFD=______.
5、如图，已知M、N两点在正方形ABCD的对角线BD上移动，∠MCN=45°，连结AM、AN，并延长分别交BC、CD于E、F两点，则∠CME+∠CNF=__________.
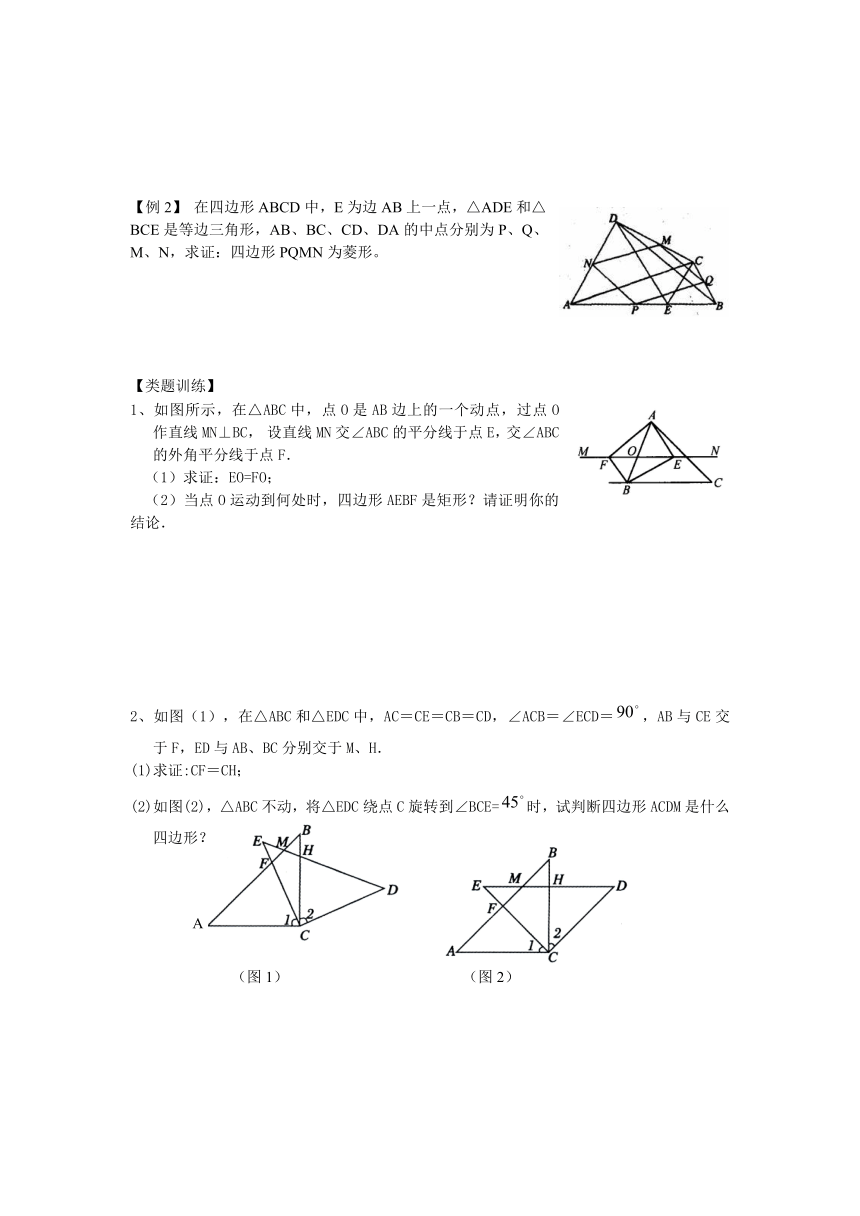
【例2】 在四边形ABCD中，E为边AB上一点，△ADE和△BCE是等边三角形，AB、BC、CD、DA的中点分别为P、Q、M、N，求证：四边形PQMN为菱形。
【类题训练】
1、如图所示，在△ABC中，点O是AB边上的一个动点，过点O作直线MN⊥BC，设直线MN交∠ABC的平分线于点E，交∠ABC的外角平分线于点F．
（1）求证：EO=FO；
（2）当点O运动到何处时，四边形AEBF是矩形？请证明你的结论．
2、如图（1），在△ABC和△EDC中，AC＝CE＝CB＝CD，∠ACB＝∠ECD＝，AB与CE交于F，ED与AB、BC分别交于M、H．
(1)求证:CF＝CH；
(2)如图(2)，△ABC不动，将△EDC绕点C旋转到∠BCE=时，试判断四边形ACDM是什么四边形？并证明你的结论．

3、已知：如图，在正方形ABCD中，点E、F分别在BC和CD上，AE = AF．连接AC交EF于点O，延长OC至点M，使OM = OA，连接EM、FM．判断四边形AEMF是什么特殊四边形？并证明你的结论．
【例3】如图所示，在梯形ABCD中，AD∥BC，∠B=90°，AD=24cm，AB=8cm，BC=26cm，动点P从A点开始沿AD边以1cm/s的速度向点D运动，动点Q从C点开始沿CB边以3cm/s的速度向点B运动，P，Q分别从A，C同时出发，当其中一个动点到达终点时，另一个动点也随之停止运动．设运动的时间为t（s）．
（1）当t为何值时，四边形ABQP是矩形？
（2）当t为何值时，四边形PQCD是平行四边形？
（3）当t为何值时，四边形PQCD是等腰梯形．
【类题训练】
1、（2010宁德）如图，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM.
⑴ 求证：△AMB≌△ENB；
⑵ ①当M点在何处时，AM＋CM的值最小；
②当M点在何处时，AM＋BM＋CM的值最小，并说明理由；
⑶ 当AM＋BM＋CM的最小值为时，求正方形的边长.
【例4】如图2-37所示．正方形ABCD中，在AD的延长线上取点E，F，使DE=AD，DF=BD，连接BF分别交CD，CE于H，G．求证：△GHD是等腰三角形．
　
【类题训练】
1、已知：如图，以正方形ABCD的对角线为边作菱形AEFC，B在FE的延长线上．
求证：AE、AF把∠BAC三等分．