1.3.3 二次根式的应用 课件(共22张PPT)
文档属性
| 名称 | 1.3.3 二次根式的应用 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 14:04:49 | ||
图片预览







文档简介
(共22张PPT)
1.3.3 二次根式的应用
浙教版 八年级下册
新知导入
二次根式的混合运算,先要弄清运算种类,再确定运算顺序:先乘除,再加减,有括号的要算括号内的,最后按照二次根式的相应的运算法则进行.
二次根式乘法法则:
二次根式加减法法则:
二次根式除法法则:
二次根式加减时,可以先将二次根式化为最简二次根式,再将同类二次根式进行合并。(口诀:一化二找三合并)
二次根式混合运算法则:
二次根式的运算法则
新知讲解
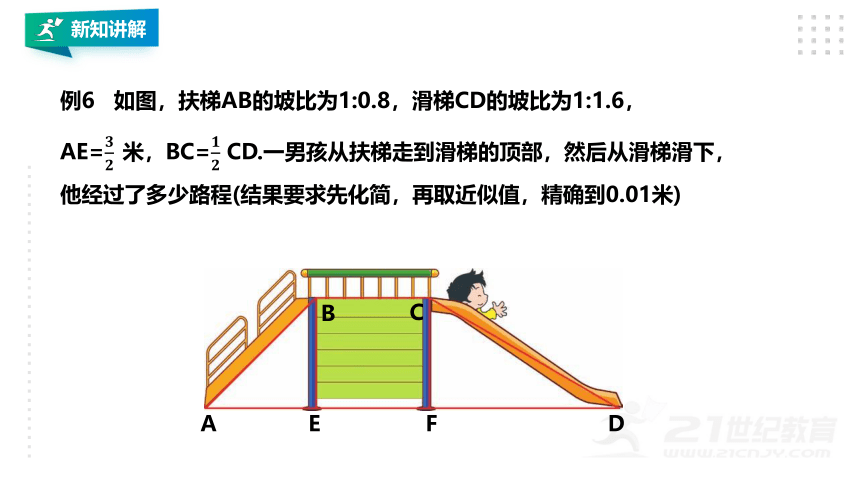
例6 如图,扶梯AB的坡比为1:0.8,滑梯CD的坡比为1:1.6,
AE=米,BC= CD.一男孩从扶梯走到滑梯的顶部,然后从滑梯滑下,他经过了多少路程(结果要求先化简,再取近似值,精确到0.01米)
A
E
F
D
B
C
解:在Rt△AEB中,AE= 米,BE= ÷0.8= 米
在Rt△CFD中,DF= ×1.6=3米
答:这个男孩经过的总路程约为7.71米.
新知讲解
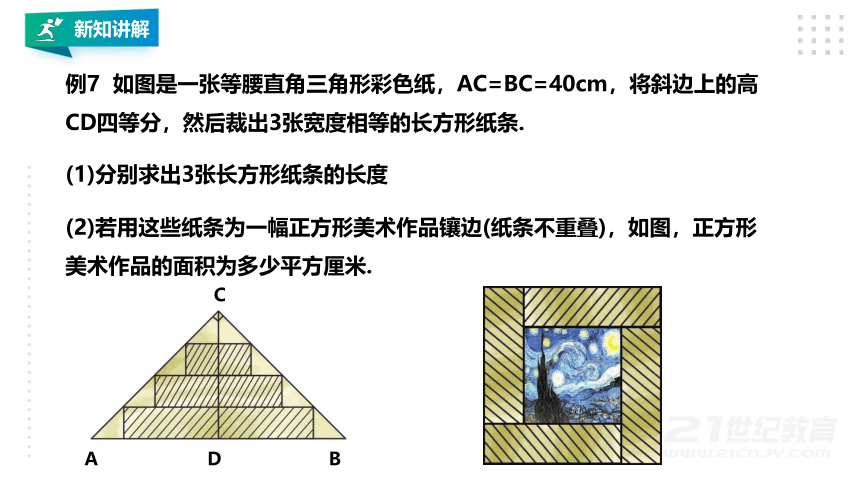
例7 如图是一张等腰直角三角形彩色纸,AC=BC=40cm,将斜边上的高CD四等分,然后裁出3张宽度相等的长方形纸条.
(1)分别求出3张长方形纸条的长度
C
A
D
B
(2)若用这些纸条为一幅正方形美术作品镶边(纸条不重叠),如图,正方形美术作品的面积为多少平方厘米.
新知讲解
解:(1)在Rt△ABC中,AC=BC=40cm,
∵ CD⊥AB,AD=BD ,
∵最上面长方形纸条的长是 CD的2倍
∴其长度为2× CD=2×5=10cm.
新知讲解
2× CD=2×10=20 cm
同理可得,其余两张长方形纸条的长度依次为:
2× CD=2×15=30 cm
答:三张长方形纸条的长度分别为10cm,20 cm,30 cm
新知讲解
(2)三张长方形纸条连接在一起的总长度为
因此,给这幅美术作品所镶的边框可以看做由四张宽为cm,长为cm的彩色纸条围成.
则正方形的边长=-=
正方形的面积=
答:这幅正方形美术作品的面积为200cm2.
新知讲解
应用二次根式及其运算解决简单实际问题要注意两个方面:
一是用二次根式或含二次根式的代数式表示未知量;
二是通过二次根式的四则混合运算求出未知量,并化简.
新知讲解
D
课堂练习
B
课堂练习
C
课堂练习
4. 已知 ,求 的值;
解:x2-2x + 1=(x -1)2
课堂练习
5.已知的整数部分是a,小数部分是b,求a2-b2的值.
解:∵3
课堂练习
6.在一个边长为 cm的正方形内部,挖去一个边长为
cm的正方形,求剩余部分的面积.
解:由题意得
答:剩余部分的面积是
课堂练习
课堂练习
课堂练习
8.甲、乙两个城市间计划修建一条城际铁路, 其中有一段路基的横断面设计为上底宽 ,下底宽,高的梯形,这段路基长 500 m,那么这段路基的土石方 (即路基的体积,其中路基的体积=路基横断面面积×路基的长度)为多少立方米呢?
课堂练习
解:因为路基的土石方等于路基横断面面积乘以路基的长度,所以这段路基的土石方为:
即这段路基的土石方为
课堂练习
应用二次根式及其运算解决简单实际问题要注意两个方面:
一是用二次根式或含二次根式的代数式表示未知量;
二是通过二次根式的四则混合运算求出未知量,并化简.
课堂小结
https://www.21cnjy.com/help/help_extract.php
1.3.3 二次根式的应用
浙教版 八年级下册
新知导入
二次根式的混合运算,先要弄清运算种类,再确定运算顺序:先乘除,再加减,有括号的要算括号内的,最后按照二次根式的相应的运算法则进行.
二次根式乘法法则:
二次根式加减法法则:
二次根式除法法则:
二次根式加减时,可以先将二次根式化为最简二次根式,再将同类二次根式进行合并。(口诀:一化二找三合并)
二次根式混合运算法则:
二次根式的运算法则
新知讲解
例6 如图,扶梯AB的坡比为1:0.8,滑梯CD的坡比为1:1.6,
AE=米,BC= CD.一男孩从扶梯走到滑梯的顶部,然后从滑梯滑下,他经过了多少路程(结果要求先化简,再取近似值,精确到0.01米)
A
E
F
D
B
C
解:在Rt△AEB中,AE= 米,BE= ÷0.8= 米
在Rt△CFD中,DF= ×1.6=3米
答:这个男孩经过的总路程约为7.71米.
新知讲解
例7 如图是一张等腰直角三角形彩色纸,AC=BC=40cm,将斜边上的高CD四等分,然后裁出3张宽度相等的长方形纸条.
(1)分别求出3张长方形纸条的长度
C
A
D
B
(2)若用这些纸条为一幅正方形美术作品镶边(纸条不重叠),如图,正方形美术作品的面积为多少平方厘米.
新知讲解
解:(1)在Rt△ABC中,AC=BC=40cm,
∵ CD⊥AB,AD=BD ,
∵最上面长方形纸条的长是 CD的2倍
∴其长度为2× CD=2×5=10cm.
新知讲解
2× CD=2×10=20 cm
同理可得,其余两张长方形纸条的长度依次为:
2× CD=2×15=30 cm
答:三张长方形纸条的长度分别为10cm,20 cm,30 cm
新知讲解
(2)三张长方形纸条连接在一起的总长度为
因此,给这幅美术作品所镶的边框可以看做由四张宽为cm,长为cm的彩色纸条围成.
则正方形的边长=-=
正方形的面积=
答:这幅正方形美术作品的面积为200cm2.
新知讲解
应用二次根式及其运算解决简单实际问题要注意两个方面:
一是用二次根式或含二次根式的代数式表示未知量;
二是通过二次根式的四则混合运算求出未知量,并化简.
新知讲解
D
课堂练习
B
课堂练习
C
课堂练习
4. 已知 ,求 的值;
解:x2-2x + 1=(x -1)2
课堂练习
5.已知的整数部分是a,小数部分是b,求a2-b2的值.
解:∵3
课堂练习
6.在一个边长为 cm的正方形内部,挖去一个边长为
cm的正方形,求剩余部分的面积.
解:由题意得
答:剩余部分的面积是
课堂练习
课堂练习
课堂练习
8.甲、乙两个城市间计划修建一条城际铁路, 其中有一段路基的横断面设计为上底宽 ,下底宽,高的梯形,这段路基长 500 m,那么这段路基的土石方 (即路基的体积,其中路基的体积=路基横断面面积×路基的长度)为多少立方米呢?
课堂练习
解:因为路基的土石方等于路基横断面面积乘以路基的长度,所以这段路基的土石方为:
即这段路基的土石方为
课堂练习
应用二次根式及其运算解决简单实际问题要注意两个方面:
一是用二次根式或含二次根式的代数式表示未知量;
二是通过二次根式的四则混合运算求出未知量,并化简.
课堂小结
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
