2.1 一元二次方程 课件(共18张PPT)
文档属性
| 名称 | 2.1 一元二次方程 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
2.1 一元二次方程
浙教版 八年级下册
新知导入
情境引入
一切问题都可以转化为数学问题,
一切数学问题都可以转化为代数问题,
而一切代数问题又可以转化为方程问题,
因此,一旦解决了方程问题,
一切问题都将迎刃而解!
------笛卡儿[Descartes, Rene du Perron, 1596-1650 ]
新知导入
什么是方程?
什么是一元一次方程?
含有未知数的等式叫做方程
方程两边都是整式,只含有一个未知数(元),并且未知数的次数是一次,这样的方程我们叫一元一次方程
一元一次方程能解决所有问题吗?
新知导入
(1)把面积为4m2的一张纸分割成如图的正方形和长方形两部分,求正方形的边长。
设正方形的边长为x,可列出方程_______________.
试着列出下列问题中关于未知数x的方程:
(2)某放射性元素经过2天质量衰变为原来的,问:平均每天的减少率为多少?
设平均每天的减少率为x,可列出方程:______________________。
3
x
x
x
x2+3x=4
新知导入
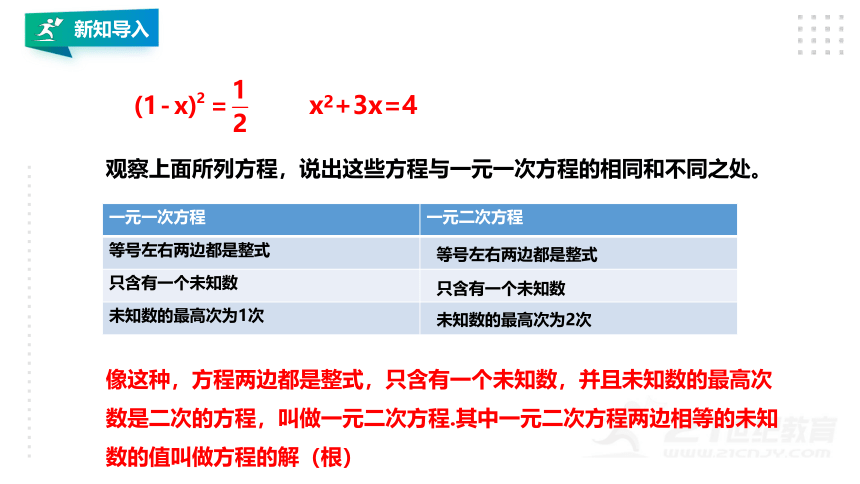
x2+3x=4
观察上面所列方程,说出这些方程与一元一次方程的相同和不同之处。
一元一次方程 一元二次方程
等号左右两边都是整式
只含有一个未知数
未知数的最高次为1次
等号左右两边都是整式
只含有一个未知数
未知数的最高次为2次
像这种,方程两边都是整式,只含有一个未知数,并且未知数的最高次数是二次的方程,叫做一元二次方程.其中一元二次方程两边相等的未知数的值叫做方程的解(根)
新知导入
我们学过了完全平方式,你能用完全平放式将变形吗?
因此, 可以变形为:
移项之后就是:
也可以变形为:
新知导入
一般地,任何一个关于x的一元二次方程都可以化为ax2+bx+c=0的形式,我们把ax2+bx+c=0 (a,b,c为常数,a≠0)称为一元二次方程的一般形式.
其中ax2,bx,c分别称为二次项,一次项,常数项;
a,b分别称为二次项系数,一次项系数.
注意:二次项系数a≠0
新知讲解
例1 把下列方程化成一元二次方程的一般形式,并写出它的二次项系数、
一次项系数和常数项.
(1)9x2=5-4x; (2)(2-x)(3x+4)=3.
解:(1)移项,整理得9x2+4x-5=0
这个方程的二次项系数是9,一次项系数是4,常数项是-5。
(2)方程左边多项式相乘,得-3x2+2x+8=3,
移项,整理得-3x2+2x+5=0
这个方程的二次项系数是-3,一次项系数是2,常数项是5。
合作探究
例2 已知一元二次方程 2x2+bx+c=0的两个根分别为x1= 和x2=-3,求这个方程.
解得
所以这个一元二次方程是2x2+x-15=0
解:将x1= 和x2=-3带入方程 2x2+bx+c=0得
2×()2+b+c=0
2×(-3)2+(-3)b+c=0
b=1
c=-15
课堂练习
B
B
课堂练习
B
1
课堂练习
5.若m是一元二次方程x2﹣2x﹣1=0的一个根,求代数式2m2﹣4m+3的值.
解:把x=m代入x2﹣2x﹣1=0,得
m2﹣2m﹣1=0,
则m2﹣2m=1.
所以4m2﹣4m+3=2(m2﹣2m)+3=2+3=5.
课堂练习
6.已知关于x的方程(k2﹣4)x2+(k﹣2)x=0.
(1)当k为何值时,此方程是一元一次方程?
(2)当k为何值时,此方程是一元二次方程?并写出这个一元二次方程的二次项系数、一次项系数和常数项.
解:(1)根据题意,得k2﹣4=0且k﹣2≠0.
解得k=﹣2.
所以当k=﹣2时,此方程是一元一次方程;
(2)根据题意,得k2﹣4≠0.
解得k≠±2.
此时一元二次方程的二次项系数是k2﹣4、一次项系数是k﹣2,常数项是0.
课堂总结
板书设计
1.一元二次方程与一元一次方程的区别:
①方程两边都是整式
②只含有一个未知数
③未知数的最高次数是2次
2.一元二次方程的解(根):能使一元二次方程等号左右两边相等的值
3.一元二次方程的形式:ax2+bx+c=0
作业布置
课本 P28 作业题
https://www.21cnjy.com/help/help_extract.php
2.1 一元二次方程
浙教版 八年级下册
新知导入
情境引入
一切问题都可以转化为数学问题,
一切数学问题都可以转化为代数问题,
而一切代数问题又可以转化为方程问题,
因此,一旦解决了方程问题,
一切问题都将迎刃而解!
------笛卡儿[Descartes, Rene du Perron, 1596-1650 ]
新知导入
什么是方程?
什么是一元一次方程?
含有未知数的等式叫做方程
方程两边都是整式,只含有一个未知数(元),并且未知数的次数是一次,这样的方程我们叫一元一次方程
一元一次方程能解决所有问题吗?
新知导入
(1)把面积为4m2的一张纸分割成如图的正方形和长方形两部分,求正方形的边长。
设正方形的边长为x,可列出方程_______________.
试着列出下列问题中关于未知数x的方程:
(2)某放射性元素经过2天质量衰变为原来的,问:平均每天的减少率为多少?
设平均每天的减少率为x,可列出方程:______________________。
3
x
x
x
x2+3x=4
新知导入
x2+3x=4
观察上面所列方程,说出这些方程与一元一次方程的相同和不同之处。
一元一次方程 一元二次方程
等号左右两边都是整式
只含有一个未知数
未知数的最高次为1次
等号左右两边都是整式
只含有一个未知数
未知数的最高次为2次
像这种,方程两边都是整式,只含有一个未知数,并且未知数的最高次数是二次的方程,叫做一元二次方程.其中一元二次方程两边相等的未知数的值叫做方程的解(根)
新知导入
我们学过了完全平方式,你能用完全平放式将变形吗?
因此, 可以变形为:
移项之后就是:
也可以变形为:
新知导入
一般地,任何一个关于x的一元二次方程都可以化为ax2+bx+c=0的形式,我们把ax2+bx+c=0 (a,b,c为常数,a≠0)称为一元二次方程的一般形式.
其中ax2,bx,c分别称为二次项,一次项,常数项;
a,b分别称为二次项系数,一次项系数.
注意:二次项系数a≠0
新知讲解
例1 把下列方程化成一元二次方程的一般形式,并写出它的二次项系数、
一次项系数和常数项.
(1)9x2=5-4x; (2)(2-x)(3x+4)=3.
解:(1)移项,整理得9x2+4x-5=0
这个方程的二次项系数是9,一次项系数是4,常数项是-5。
(2)方程左边多项式相乘,得-3x2+2x+8=3,
移项,整理得-3x2+2x+5=0
这个方程的二次项系数是-3,一次项系数是2,常数项是5。
合作探究
例2 已知一元二次方程 2x2+bx+c=0的两个根分别为x1= 和x2=-3,求这个方程.
解得
所以这个一元二次方程是2x2+x-15=0
解:将x1= 和x2=-3带入方程 2x2+bx+c=0得
2×()2+b+c=0
2×(-3)2+(-3)b+c=0
b=1
c=-15
课堂练习
B
B
课堂练习
B
1
课堂练习
5.若m是一元二次方程x2﹣2x﹣1=0的一个根,求代数式2m2﹣4m+3的值.
解:把x=m代入x2﹣2x﹣1=0,得
m2﹣2m﹣1=0,
则m2﹣2m=1.
所以4m2﹣4m+3=2(m2﹣2m)+3=2+3=5.
课堂练习
6.已知关于x的方程(k2﹣4)x2+(k﹣2)x=0.
(1)当k为何值时,此方程是一元一次方程?
(2)当k为何值时,此方程是一元二次方程?并写出这个一元二次方程的二次项系数、一次项系数和常数项.
解:(1)根据题意,得k2﹣4=0且k﹣2≠0.
解得k=﹣2.
所以当k=﹣2时,此方程是一元一次方程;
(2)根据题意,得k2﹣4≠0.
解得k≠±2.
此时一元二次方程的二次项系数是k2﹣4、一次项系数是k﹣2,常数项是0.
课堂总结
板书设计
1.一元二次方程与一元一次方程的区别:
①方程两边都是整式
②只含有一个未知数
③未知数的最高次数是2次
2.一元二次方程的解(根):能使一元二次方程等号左右两边相等的值
3.一元二次方程的形式:ax2+bx+c=0
作业布置
课本 P28 作业题
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
