5.2不等式的基本性质

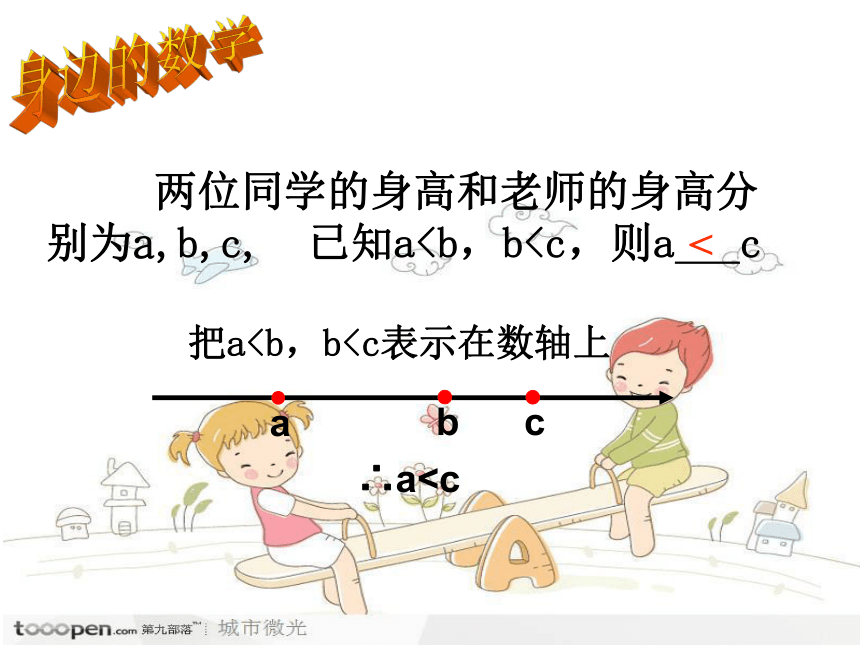
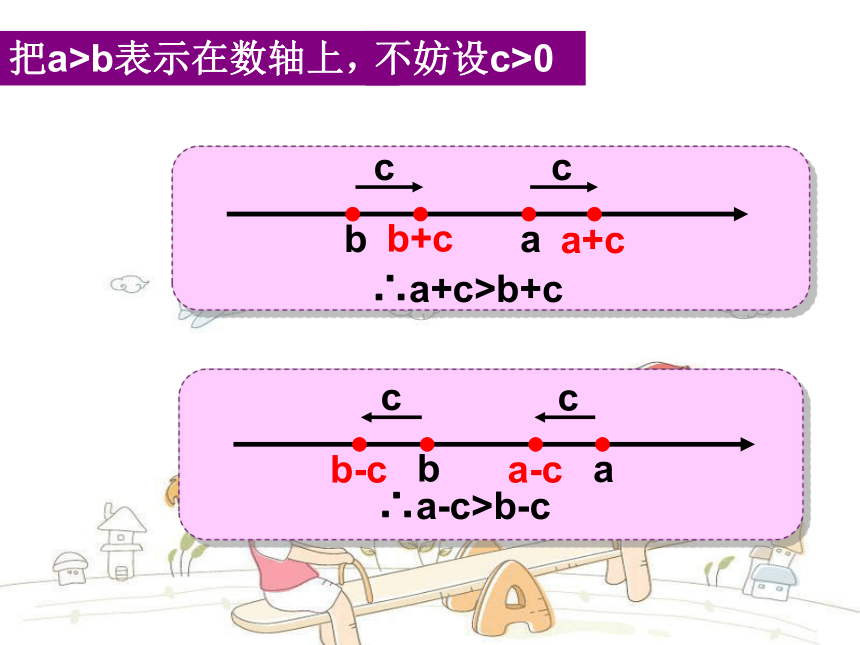
课件20张PPT。 两位同学的身高和老师的身高分别为a,b,c, 已知ab表示在数轴上，不妨设c>0∴a+c>b+c∴a-c>b-c身边的数学 两位同学平均每天的零花钱分别为5元和8元，那么一周下来谁花得更多？一起来探索吧!不等式的两边都乘以(或除以)同一个数，
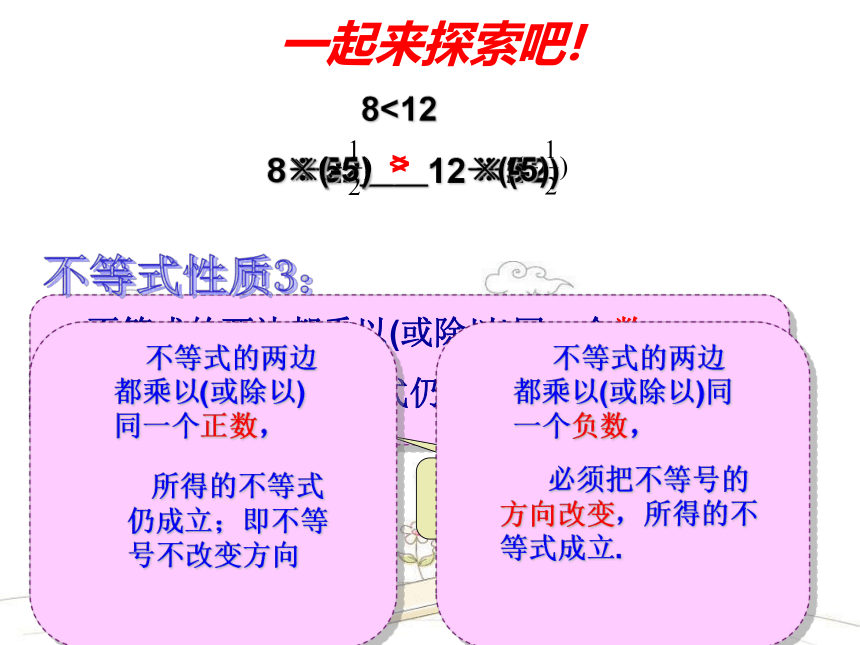
所得的不等式仍成立；是这样的吗? 8<12 不等式的两边都乘以(或除以)同一个正数，
不等式的两边都乘以(或除以)同一个负数， 必须把不等号的方向改变，所得的不等式成立.
所得的不等式仍成立；即不等号不改变方向 8 ＿＿12×2 ×2
÷5 ÷5
×(-2) ×(-2)
÷(-5) ÷(-5)
× ×
<>不等式性质3：< 6＞2,
6×5____2×5 ,
><6×(-5)____2×(-5)
-1<4,
-1+3____4+3,

-1-5____4-5
<<趁热打铁温馨小归纳： 只有当不等式两边都乘以（或除以）同一个___ 时， 不等号才需要 ____
负数改变方向 若a>-3，则a+3____0；
若a+3>0，则a ____-3，>>若 -0.5 x≤1,两边同乘以-2,得________,
依据_______________ ；
x≥－2不等式的基本性质3
（1）若m>n，n>q,则m q
(依据： )＞不等式的基本性质1（2）若x＋1>0，两边同时加上－1，得 。
（依据 ）X>－1不等式的基本性质2相信你能行Ａ逆向思维Cax ≤ay 若a 则 a____ b<2 + 2+m m>(m>0)(m<0)(m=0)>=相信你能行试比较2a与a的大小.想一想：你能用哪些方法呢？123例若改为a>0和a=0呢？已知a<0 ，解：∵x＜y∴-3x＞-3y（不等式性质3）∴2-3x＞2-3y（不等式性质2）例 国际上广泛使用“身体体重指数（BMI）”作为判断人体健康状况的一个指标。这个指数B等于人体的体重G（千克）除以人体身高h（米）的平方所得的商。（1）写出身体体重指数B与G、h之间的关系式（2）上表是国内健康组织提供的参考标准，若黄老师体重是G=56千克，身高h=1.71米,请问我的体型属于哪一型?(3) 那么我的体重在什么范围内,体型属于正常?身边的数学 回顾不等式的性质：有所得数学在身边1：不等式的传递性：若a所得的不等式仍成立。3：不等式两边都乘以（或除以）同一个正数，
所得的不等式仍成立。不等式的两边都乘以(或除以)同一个负数，
必须把不等号的方向改变，所得的不等式成立.作业 1. 课内练习：１，２
　　　2.作业本拓展与延伸 若x(a-3)y,求a的取值范围解法一：∵2＞1，a＜0，
∴2a＜a（不等式的基本性质3）返回已知a<0 ，试比较2a与a的大小.例解法二：在数轴上分别表示2a和a的点
（a＜0），如图.2a位于a的左边，
所以2a＜a 返回已知a<0 ，试比较2a与a的大小.例 解法三:
∵ a＜0,
∴ a+a ＜ a
∴2a