第4章平行四边形章节练习(4.3-4.5)(含答案)
文档属性
| 名称 | 第4章平行四边形章节练习(4.3-4.5)(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-08 22:44:19 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第4章章节练习
[范围:4.3~4.5]
一、选择题(每小题4分,共32分)
1.观察下列图案,是轴对称图形而不是中心对称图形的是 ( )
图3-G-1
2.满足下列条件的四边形,不一定是平行四边形的是 ( )
A.两组对边分别平行
B.两组对边分别相等
C.一组对边平行且相等
D.一组对边平行,另一组对边相等
3.已知点A(a,2021)与点A'(-2022,b)关于原点O对称,则a+b的值为 ( )
A.1 B.5 C.6 D.4
4.如图3-G-2,在△ABC中,D,E,F分别是边AB,BC,AC的中点.若AB=AC=2,则四边形ADEF的周长为 ( )
图3-G-2
A.1 B.2 C.4 D.8
5.已知四边形的四条边的长分别是m,n,p,q,且满足m2+n2+p2+q2=2mn+2pq,则这个四边形是( )
A.平行四边形
B.对角线互相垂直的四边形
C.平行四边形或对角线互相垂直的四边形
D.对角线相等的四边形
6.如图3-G-3,在 ABCD中,E,F分别为边BC,AD的中点,则图中平行四边形的个数是 ( )
图3-G-3
A.3 B.4 C.5 D.6
7.在4×4的正方形网格中每个小正方形的边长均为1,每个小正方形的顶点叫做格点,点A,B(均在格点上)的位置如图3-G-4,若以A,B为顶点画面积为2的格点平行四边形,则符合条件的平行四边形的个数是 ( )
图3-G-4
A.6 B.7 C.9 D.11
8.如图3-G-5,在Rt△ABC中,∠C=90°,AB=10 cm,AC=8 cm,D是AC上一点,以AD,BD为邻边作平行四边形ADBE,则对角线DE的最小值是 ( )
图3-G-5
A.4 cm B.6 cm C.8 cm D.10 cm
二、填空题(每小题4分,共24分)
9.如图3-G-6,OA=OC,BD=16 cm,则当OB= cm时,四边形ABCD是平行四边形.
图3-G-6
10.如图3-G-7所示,E,F是 ABCD对角线BD上的两点,请你添加一个适当的条件: ,使四边形AECF是平行四边形.
图3-G-7
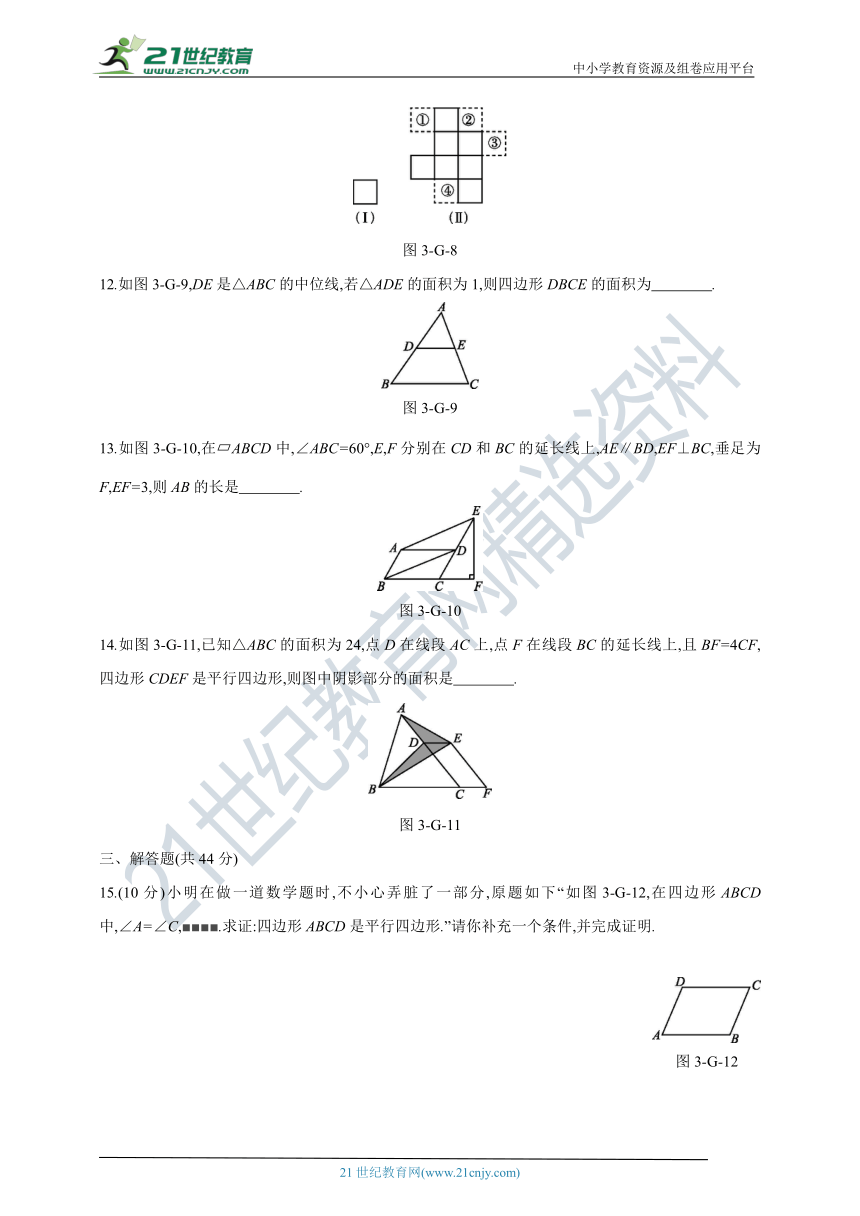
11.图3-G-8 (Ⅰ)和(Ⅱ)中的小正方形都全等,将图(Ⅰ)的正方形放在图(Ⅱ)中①②③④的某一位置,使它与原来的7个小正方形组成中心对称图形,这个位置是 .
图3-G-8
12.如图3-G-9,DE是△ABC的中位线,若△ADE的面积为1,则四边形DBCE的面积为 .
图3-G-9
13.如图3-G-10,在 ABCD中,∠ABC=60°,E,F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,垂足为F,EF=3,则AB的长是 .
图3-G-10
14.如图3-G-11,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BF=4CF,四边形CDEF是平行四边形,则图中阴影部分的面积是 .
图3-G-11
三、解答题(共44分)
15.(10分)小明在做一道数学题时,不小心弄脏了一部分,原题如下“如图3-G-12,在四边形ABCD中,∠A=∠C,■■■■.求证:四边形ABCD是平行四边形.”请你补充一个条件,并完成证明.
图3-G-12
16.(10分)如图3-G-13,在四边形ABCD中,AB=CD,AD=BC.求证:∠A=∠C.
图3-G-13
17.(12分)如图3-G-14,在四边形ABCD中,AB∥CD,AE⊥BD,CF⊥BD,垂足分别为E,F,BF=DE,连结AC.
求证:(1)△ABE≌△CDF;
(2)AC与BD互相平分.
图3-G-14
18.(12分)如图3-G-15,在四边形ABCD中,AD∥BC,AC,BD相交于点E,E是BD的中点,延长CD到点F,使DF=CD,连结AF.
(1)求证:AE=CE;
(2)求证:四边形ABDF是平行四边形;
(3)若AD=,AF=4,DF=,则四边形ABCF的面积为 .
图3-G-15
详解详析
1.A [解析] A项,是轴对称图形,不是中心对称图形,故本选项符合题意;
B项,不是轴对称图形,是中心对称图形,故本选项不符合题意;
C项,不是轴对称图形,是中心对称图形,故本选项不符合题意;
D项,是轴对称图形,也是中心对称图形,故本选项不符合题意.
故选A.
2.D
3.A [解析] ∵点A(a,2021)与点A'(-2022,b)关于原点O对称,∴a=2022,b=-2021,
∴a+b=1.
故选A.
4.C
5.C [解析] ∵m2+n2+p2+q2=2mn+2pq,
∴(m-n)2+(p-q)2=0,
∴m=n,p=q.
∵m,n,p,q为四边形的四边长,
当m,n为对边,p,q为对边时,
可确定这个四边形为平行四边形;
当m,n为邻边时,可以证明有两个顶点在一条对角线的垂直平分线上,
∴四边形是对角线互相垂直的四边形.
6.B [解析] ∵E,F分别为边BC,AD的中点,∴AF=DF,BE=EC.
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴AF=DF=BE=EC,
则AFBE,DFEC,AFEC,
∴四边形ABEF是平行四边形,四边形FECD是平行四边形,四边形AECF是平行四边形,
则图中平行四边形的个数是4.故选B.
7.D [解析] 符合条件的平行四边形如图所示,共11个,故选D.
8.B [解析] 如图,设AB与DE相交于点O.
∵在Rt△ABC中,∠C=90°,
∴BC⊥AC.
∵四边形ADBE是平行四边形,
∴OD=OE,OA=OB,
∴当OD取最小值时,线段DE最短,此时OD⊥AC,
∴OD∥CB.
又O是AB的中点,
∴OD是△ABC的中位线,
∴OD=CB.
∵∠C=90°,AB=10 cm,AC=8 cm,
∴CB===6(cm),
∴OD=3 cm,
∴DE=2OD=6 cm.
故选B.
9.8 [解析] ∵BD=16 cm,OB=8 cm,
∴OD=BD-OB=8 cm,
∴OB=OD.
又∵OA=OC,
∴四边形ABCD是平行四边形.
故答案为8.
10.BE=DF(答案不唯一)
11.③ [解析] 当正方形放在③的位置时,能组成中心对称图形.
故答案为③.
12.3 [解析] 如图,连结BE.
∵D是AB的中点,
∴S△ADE=S△BDE,
∴S△ABE=2S△ADE=2.
∵E是AC的中点,
∴S△ABC=2S△ABE=4,
∴S四边形DBCE=S△ABC-S△ADE=4-1=3.
13. [解析] ∵四边形ABCD是平行四边形,
∴AB∥DC,AB=CD.
∵AE∥BD,
∴四边形ABDE是平行四边形,
∴AB=DE,
∴DE=CD,
即D为CE的中点.
∵EF⊥BC,
∴∠EFC=90°.
∵AB∥CD,
∴∠DCF=∠ABC=60°,
∴∠CEF=30°.
∵EF=3,
∴CE=2,
∴AB=.
故答案为.
14.8 [解析] 如图,连结EC,过点A作AM∥BC交FE的延长线于点M.
∵四边形CDEF是平行四边形,
∵DE∥CF,EF∥CD,
∴AM∥DE∥CF,AC∥FM,
∴四边形ACFM,ADEM是平行四边形.
∵△BDE的DE边上的高线和△CDE的DE边上的高线相同,
∴△BDE的面积和△CDE的面积相等.
又△ADE的面积和△AME的面积相等,△DCE的面积和△FEC的面积相等,
∴阴影部分的面积等于平行四边形ACFM的面积的一半,是CF·hCF(hCF为平行四边形ACFM的CF边上的高线长).
∵△ABC的面积是24,BF=4CF,
∴BC=3CF,
∴BC·hBC=×3CF·hCF=24(hBC为△ABC的BC边上的高线长),
∴CF·hCF=16,
∴阴影部分的面积是CF·hCF=×16=8.
15.解:答案不唯一,如∠A+∠B=180°等.
以添加∠A+∠B=180°为例证明:
∵∠A+∠B=180°,
∴AD∥BC.
∵∠A=∠C,∴∠B+∠C=180°,
∴AB∥CD,
∴四边形ABCD是平行四边形.
16.证明:∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
∴∠A=∠C.
17.证明:(1)∵AB∥CD,∴∠ABE=∠CDF.
∵BF=DE,
∴BF-EF=DE-EF,即BE=DF.
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
∴△ABE≌△CDF.
(2)∵△ABE≌△CDF,
∴AB=CD.
又∵AB∥CD,
∴四边形ABCD是平行四边形,
∴AC与BD互相平分.
18.解:(1)证明:∵E是BD的中点,
∴BE=DE.
∵AD∥BC,
∴∠ADE=∠CBE.
在△ADE和△CBE中,
∵
∴△ADE≌△CBE(ASA),
∴AE=CE.
(2)证明:∵AE=CE,BE=DE,
∴四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵DF=CD,∴DF=AB.
∵AB∥CD,点F在CD的延长线上,
∴AB∥DF,
∴四边形ABDF是平行四边形.
(3)6 [解析] 如图,过点D作DQ⊥AF于点Q.
设QF=x.
∵AD=,AF=4,DF=,
DF2-QF2=AD2-AQ2,
∴2-x2=2-(4-x)2,
解得x=,
∴QD=1,
∴四边形ABCF的面积=3S△ADF=3××4×1=6.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第4章章节练习
[范围:4.3~4.5]
一、选择题(每小题4分,共32分)
1.观察下列图案,是轴对称图形而不是中心对称图形的是 ( )
图3-G-1
2.满足下列条件的四边形,不一定是平行四边形的是 ( )
A.两组对边分别平行
B.两组对边分别相等
C.一组对边平行且相等
D.一组对边平行,另一组对边相等
3.已知点A(a,2021)与点A'(-2022,b)关于原点O对称,则a+b的值为 ( )
A.1 B.5 C.6 D.4
4.如图3-G-2,在△ABC中,D,E,F分别是边AB,BC,AC的中点.若AB=AC=2,则四边形ADEF的周长为 ( )
图3-G-2
A.1 B.2 C.4 D.8
5.已知四边形的四条边的长分别是m,n,p,q,且满足m2+n2+p2+q2=2mn+2pq,则这个四边形是( )
A.平行四边形
B.对角线互相垂直的四边形
C.平行四边形或对角线互相垂直的四边形
D.对角线相等的四边形
6.如图3-G-3,在 ABCD中,E,F分别为边BC,AD的中点,则图中平行四边形的个数是 ( )
图3-G-3
A.3 B.4 C.5 D.6
7.在4×4的正方形网格中每个小正方形的边长均为1,每个小正方形的顶点叫做格点,点A,B(均在格点上)的位置如图3-G-4,若以A,B为顶点画面积为2的格点平行四边形,则符合条件的平行四边形的个数是 ( )
图3-G-4
A.6 B.7 C.9 D.11
8.如图3-G-5,在Rt△ABC中,∠C=90°,AB=10 cm,AC=8 cm,D是AC上一点,以AD,BD为邻边作平行四边形ADBE,则对角线DE的最小值是 ( )
图3-G-5
A.4 cm B.6 cm C.8 cm D.10 cm
二、填空题(每小题4分,共24分)
9.如图3-G-6,OA=OC,BD=16 cm,则当OB= cm时,四边形ABCD是平行四边形.
图3-G-6
10.如图3-G-7所示,E,F是 ABCD对角线BD上的两点,请你添加一个适当的条件: ,使四边形AECF是平行四边形.
图3-G-7
11.图3-G-8 (Ⅰ)和(Ⅱ)中的小正方形都全等,将图(Ⅰ)的正方形放在图(Ⅱ)中①②③④的某一位置,使它与原来的7个小正方形组成中心对称图形,这个位置是 .
图3-G-8
12.如图3-G-9,DE是△ABC的中位线,若△ADE的面积为1,则四边形DBCE的面积为 .
图3-G-9
13.如图3-G-10,在 ABCD中,∠ABC=60°,E,F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,垂足为F,EF=3,则AB的长是 .
图3-G-10
14.如图3-G-11,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BF=4CF,四边形CDEF是平行四边形,则图中阴影部分的面积是 .
图3-G-11
三、解答题(共44分)
15.(10分)小明在做一道数学题时,不小心弄脏了一部分,原题如下“如图3-G-12,在四边形ABCD中,∠A=∠C,■■■■.求证:四边形ABCD是平行四边形.”请你补充一个条件,并完成证明.
图3-G-12
16.(10分)如图3-G-13,在四边形ABCD中,AB=CD,AD=BC.求证:∠A=∠C.
图3-G-13
17.(12分)如图3-G-14,在四边形ABCD中,AB∥CD,AE⊥BD,CF⊥BD,垂足分别为E,F,BF=DE,连结AC.
求证:(1)△ABE≌△CDF;
(2)AC与BD互相平分.
图3-G-14
18.(12分)如图3-G-15,在四边形ABCD中,AD∥BC,AC,BD相交于点E,E是BD的中点,延长CD到点F,使DF=CD,连结AF.
(1)求证:AE=CE;
(2)求证:四边形ABDF是平行四边形;
(3)若AD=,AF=4,DF=,则四边形ABCF的面积为 .
图3-G-15
详解详析
1.A [解析] A项,是轴对称图形,不是中心对称图形,故本选项符合题意;
B项,不是轴对称图形,是中心对称图形,故本选项不符合题意;
C项,不是轴对称图形,是中心对称图形,故本选项不符合题意;
D项,是轴对称图形,也是中心对称图形,故本选项不符合题意.
故选A.
2.D
3.A [解析] ∵点A(a,2021)与点A'(-2022,b)关于原点O对称,∴a=2022,b=-2021,
∴a+b=1.
故选A.
4.C
5.C [解析] ∵m2+n2+p2+q2=2mn+2pq,
∴(m-n)2+(p-q)2=0,
∴m=n,p=q.
∵m,n,p,q为四边形的四边长,
当m,n为对边,p,q为对边时,
可确定这个四边形为平行四边形;
当m,n为邻边时,可以证明有两个顶点在一条对角线的垂直平分线上,
∴四边形是对角线互相垂直的四边形.
6.B [解析] ∵E,F分别为边BC,AD的中点,∴AF=DF,BE=EC.
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴AF=DF=BE=EC,
则AFBE,DFEC,AFEC,
∴四边形ABEF是平行四边形,四边形FECD是平行四边形,四边形AECF是平行四边形,
则图中平行四边形的个数是4.故选B.
7.D [解析] 符合条件的平行四边形如图所示,共11个,故选D.
8.B [解析] 如图,设AB与DE相交于点O.
∵在Rt△ABC中,∠C=90°,
∴BC⊥AC.
∵四边形ADBE是平行四边形,
∴OD=OE,OA=OB,
∴当OD取最小值时,线段DE最短,此时OD⊥AC,
∴OD∥CB.
又O是AB的中点,
∴OD是△ABC的中位线,
∴OD=CB.
∵∠C=90°,AB=10 cm,AC=8 cm,
∴CB===6(cm),
∴OD=3 cm,
∴DE=2OD=6 cm.
故选B.
9.8 [解析] ∵BD=16 cm,OB=8 cm,
∴OD=BD-OB=8 cm,
∴OB=OD.
又∵OA=OC,
∴四边形ABCD是平行四边形.
故答案为8.
10.BE=DF(答案不唯一)
11.③ [解析] 当正方形放在③的位置时,能组成中心对称图形.
故答案为③.
12.3 [解析] 如图,连结BE.
∵D是AB的中点,
∴S△ADE=S△BDE,
∴S△ABE=2S△ADE=2.
∵E是AC的中点,
∴S△ABC=2S△ABE=4,
∴S四边形DBCE=S△ABC-S△ADE=4-1=3.
13. [解析] ∵四边形ABCD是平行四边形,
∴AB∥DC,AB=CD.
∵AE∥BD,
∴四边形ABDE是平行四边形,
∴AB=DE,
∴DE=CD,
即D为CE的中点.
∵EF⊥BC,
∴∠EFC=90°.
∵AB∥CD,
∴∠DCF=∠ABC=60°,
∴∠CEF=30°.
∵EF=3,
∴CE=2,
∴AB=.
故答案为.
14.8 [解析] 如图,连结EC,过点A作AM∥BC交FE的延长线于点M.
∵四边形CDEF是平行四边形,
∵DE∥CF,EF∥CD,
∴AM∥DE∥CF,AC∥FM,
∴四边形ACFM,ADEM是平行四边形.
∵△BDE的DE边上的高线和△CDE的DE边上的高线相同,
∴△BDE的面积和△CDE的面积相等.
又△ADE的面积和△AME的面积相等,△DCE的面积和△FEC的面积相等,
∴阴影部分的面积等于平行四边形ACFM的面积的一半,是CF·hCF(hCF为平行四边形ACFM的CF边上的高线长).
∵△ABC的面积是24,BF=4CF,
∴BC=3CF,
∴BC·hBC=×3CF·hCF=24(hBC为△ABC的BC边上的高线长),
∴CF·hCF=16,
∴阴影部分的面积是CF·hCF=×16=8.
15.解:答案不唯一,如∠A+∠B=180°等.
以添加∠A+∠B=180°为例证明:
∵∠A+∠B=180°,
∴AD∥BC.
∵∠A=∠C,∴∠B+∠C=180°,
∴AB∥CD,
∴四边形ABCD是平行四边形.
16.证明:∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
∴∠A=∠C.
17.证明:(1)∵AB∥CD,∴∠ABE=∠CDF.
∵BF=DE,
∴BF-EF=DE-EF,即BE=DF.
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
∴△ABE≌△CDF.
(2)∵△ABE≌△CDF,
∴AB=CD.
又∵AB∥CD,
∴四边形ABCD是平行四边形,
∴AC与BD互相平分.
18.解:(1)证明:∵E是BD的中点,
∴BE=DE.
∵AD∥BC,
∴∠ADE=∠CBE.
在△ADE和△CBE中,
∵
∴△ADE≌△CBE(ASA),
∴AE=CE.
(2)证明:∵AE=CE,BE=DE,
∴四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵DF=CD,∴DF=AB.
∵AB∥CD,点F在CD的延长线上,
∴AB∥DF,
∴四边形ABDF是平行四边形.
(3)6 [解析] 如图,过点D作DQ⊥AF于点Q.
设QF=x.
∵AD=,AF=4,DF=,
DF2-QF2=AD2-AQ2,
∴2-x2=2-(4-x)2,
解得x=,
∴QD=1,
∴四边形ABCF的面积=3S△ADF=3××4×1=6.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
