浙教版数学九下 3.3 由三视图描述几何体 同步练习(含解析)
文档属性
| 名称 | 浙教版数学九下 3.3 由三视图描述几何体 同步练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 729.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 00:00:00 | ||
图片预览


文档简介
第3章 三视图与表面展开图
3.3 由三视图描述几何体
知识点1 由三视图描述几何体
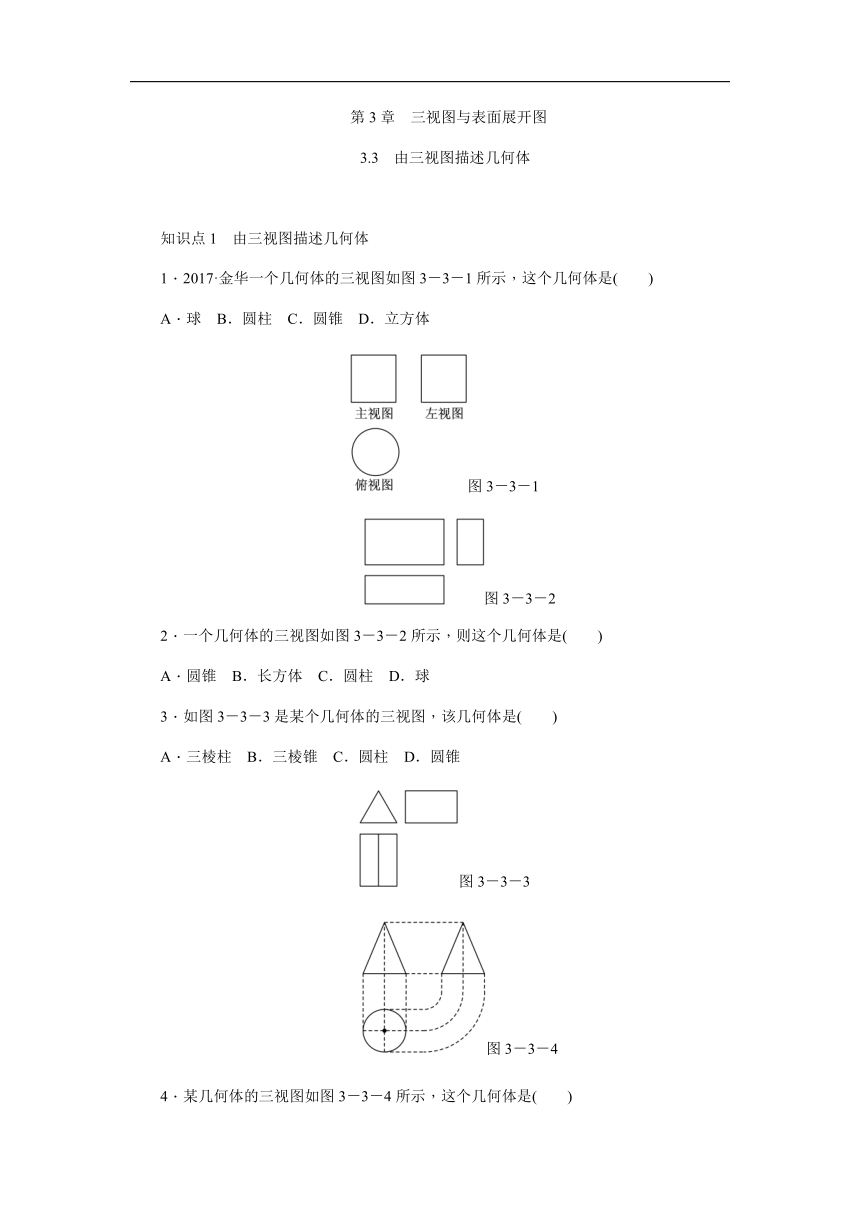
1.2017·金华一个几何体的三视图如图3-3-1所示,这个几何体是( )
A.球 B.圆柱 C.圆锥 D.立方体
图3-3-1
图3-3-2
2.一个几何体的三视图如图3-3-2所示,则这个几何体是( )
A.圆锥 B.长方体 C.圆柱 D.球
3.如图3-3-3是某个几何体的三视图,该几何体是( )
A.三棱柱 B.三棱锥 C.圆柱 D.圆锥
图3-3-3
图3-3-4
4.某几何体的三视图如图3-3-4所示,这个几何体是( )
A.圆锥 B.圆柱
C.三棱柱 D.三棱锥
图3-3-5
5.如图3-3-5是由三个相同的小正方体组成的几何体的主视图,那么这个几何体可以是( )
图3-3-6
知识点2 与三视图相关的计算问题
图3-3-7
6.由6个大小相同的正方体塔成的几何体如图3-3-7所示,比较它的主视图、左视图和俯视图的面积,则( )
A.三个视图的面积一样大
B.主视图的面积最小
C.左视图的面积最小
D.俯视图的面积最小
7.一个长方体的三视图如图3-3-8所示,则这个长方体的体积为( )
A.30 B.15 C.45 D.20
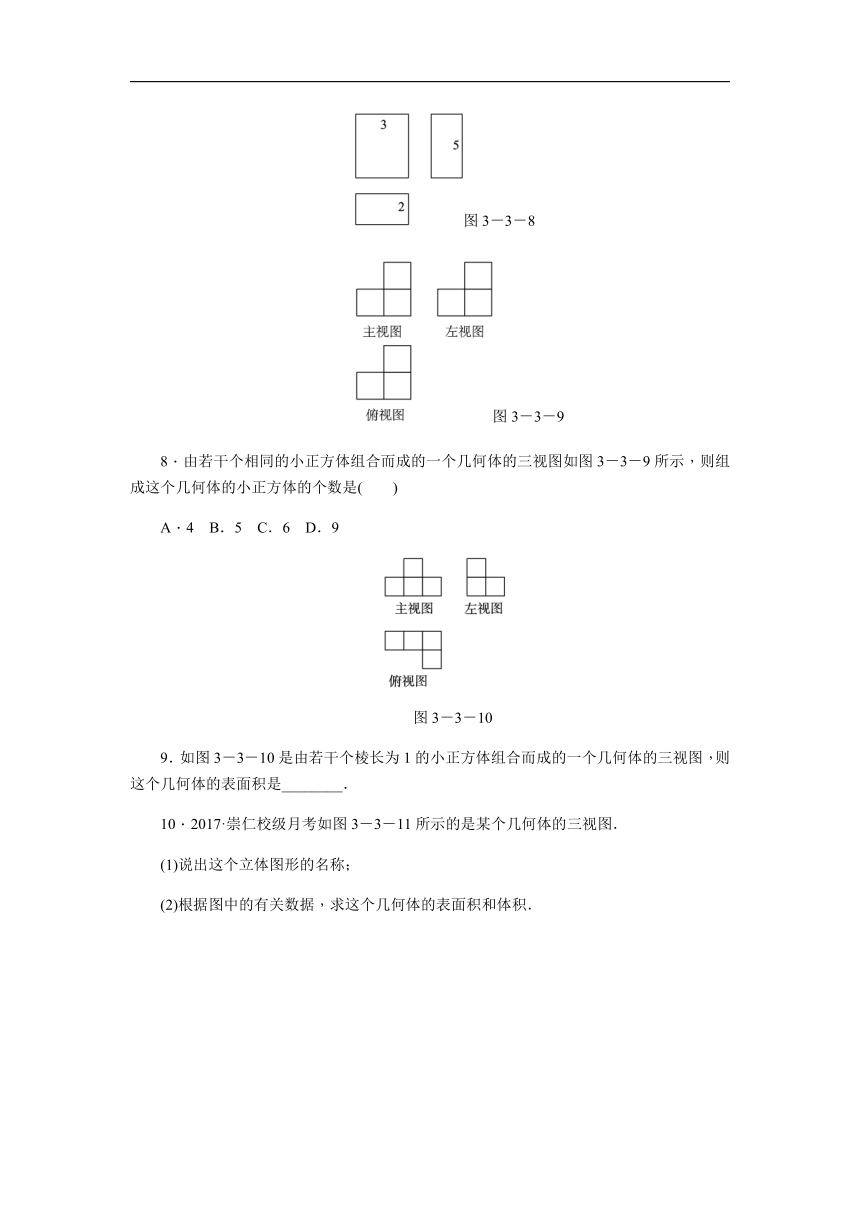
图3-3-8
图3-3-9
8.由若干个相同的小正方体组合而成的一个几何体的三视图如图3-3-9所示,则组成这个几何体的小正方体的个数是( )
A.4 B.5 C.6 D.9
图3-3-10
9.如图3-3-10是由若干个棱长为1的小正方体组合而成的一个几何体的三视图,则这个几何体的表面积是________.
10.2017·崇仁校级月考如图3-3-11所示的是某个几何体的三视图.
(1)说出这个立体图形的名称;
(2)根据图中的有关数据,求这个几何体的表面积和体积.
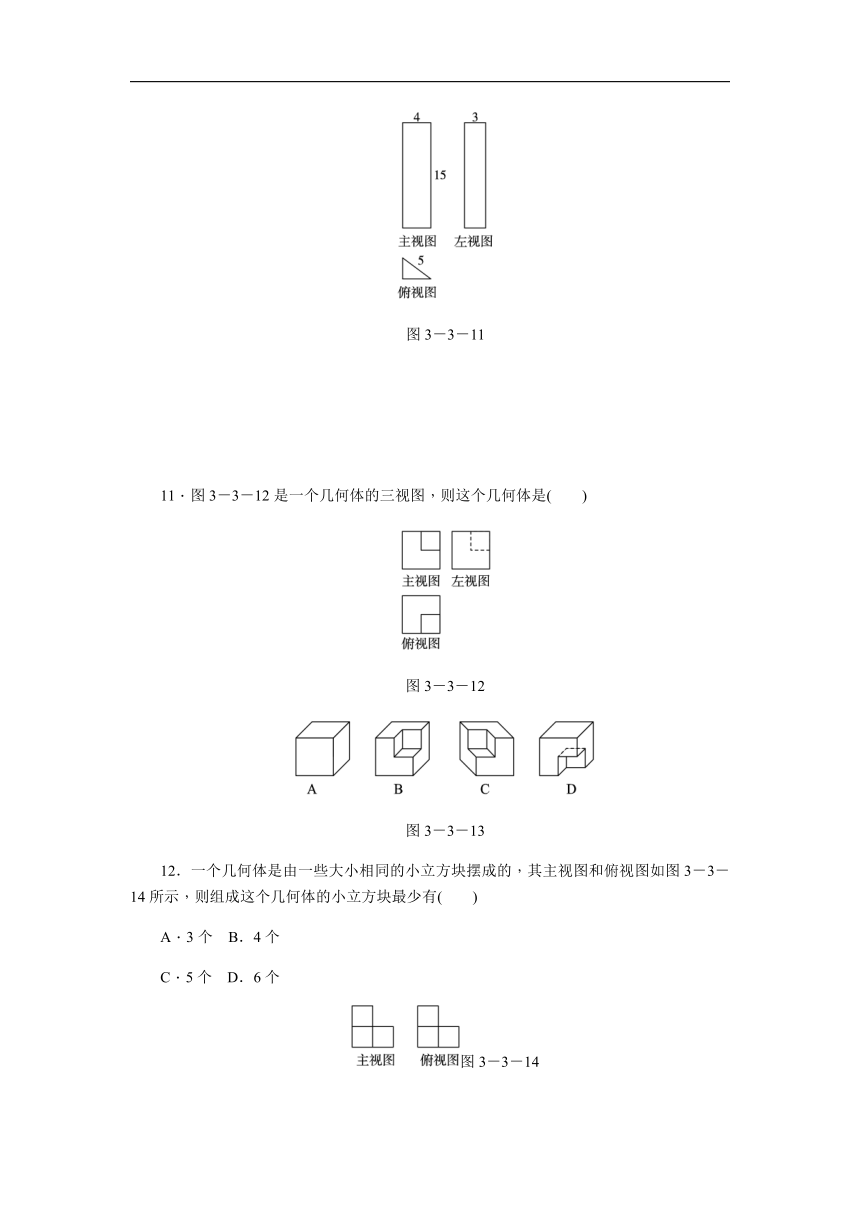
图3-3-11
11.图3-3-12是一个几何体的三视图,则这个几何体是( )
图3-3-12
图3-3-13
12.一个几何体是由一些大小相同的小立方块摆成的,其主视图和俯视图如图3-3-14所示,则组成这个几何体的小立方块最少有( )
A.3个 B.4个
C.5个 D.6个
图3-3-14
图3-3-15
13.一个几何体的主视图和俯视图如图3-3-15所示,若这个几何体最多有a个小正方体组成,最少有b个小正方体组成,则a+b的值为( )
A.10 B.11 C.12 D.13
14.如图3-3-16是某几何体的三视图,则该几何体的体积是( )
图3-3-16
A.18 B.54
C.108 D.216
15.如图3-3-17所示的三棱柱的三视图如图3-3-18所示,△EFG中,EF=8 cm,EG=12 cm,∠EGF=30°,则AB的长为________cm.
图3-3-17
图3-3-18
16.几何体的三视图相互关联.某直三棱柱的三视图如图3-3-19所示,在△PMN中,∠MPN=90°,PN=4,sin∠PMN=.
(1)求BC及FG的长;
(2)若主视图与左视图两矩形相似,求AB的长;
(3)在(2)的情况下,求直三棱柱的表面积.
图3-3-19
17.已知一个模型的三视图如图3-3-20所示(单位:m).
(1)请描述这个模型的形状;
(2)若制作这个模型的木料密度为360 kg/m3,则这个模型的质量是多少?
(3)如果用油漆漆这个模型,每千克油漆可以漆4 m2,那么需要多少千克油漆?
图3-3-20
详解详析
1.B
2.B [解析] 观察发现,主视图、左视图、俯视图都是矩形,可以确定几何体是直棱柱,所以这个几何体是长方体,故选B.
3.A 4.A 5.A
6.C [解析] 分别画出这个几何体的主视图、左视图和俯视图,假设每个正方体的棱长为1,则主视图的面积为5,左视图的面积为3,俯视图的面积为4,所以左视图的面积最小.故选C.
7.A 8.A
9.22 [解析] 由俯视图可知左下角的两个位置没有摆放正方体,再结合主视图和左视图得到如图,其中方框里的数字表示在这个位置所摆放的小正方体的个数.
10.解:(1)根据三视图可得:这个立体图形是三棱柱.
(2)这个几何体的表面积为×3×4×2+15×3+15×4+15×5=192;
体积是×3×4×15=90.
11.B [解析] 由主视图易知,只有B选项符合.
12.B [解析] 根据主视图与俯视图可得,此几何体共两层,第一层分前后两排,前一排共有2个立方块,后一排有1个立方块;第二层最少有1个立方块,因此最少有4个,故选B.
13.C [解析] 根据主视图可知俯视图中第一列最高为3个,第二列最高为1个,
∴a=3×2+1=7,b=3+1+1=5,
∴a+b=7+5=12.
14.C [解析] 由三视图可以看出:该几何体是一个正六棱柱,其中底面正六边形的边长为6,高是2,∴该几何体的体积为6××6×6××2=108 .
15.6
16.解:(1)设Rt△PMN斜边上的高为h,由图可知:
BC=MN,FG=h,
∵sin∠PMN=,PN=4,
∴MN=5,PM=3,
∴BC=5.
∵PM·PN=h·MN.
∴h=,
∴FG=.
(2)∵矩形ABCD与矩形EFGH相似,且AB=EF,∴=,
即=,∴AB=2 (负值已舍).
(3)直三棱柱的表面积为×3×4×2+5×2 +3×2 +4×2 =12+24 .
17.解:(1)此模型由两个长方体组成:上面的是小长方体,下面的是大长方体.
(2)模型的体积=3×6×6+2.5×2.5×2=120.5(m3),模型的质量=120.5×360=43380(kg).
(3)模型的表面积=2×2.5×2.5+2×2×2.5+2×6×3+2×3×6+2×6×6=166.5(m2),
需要油漆:166.5÷4=41.625(kg).
3.3 由三视图描述几何体
知识点1 由三视图描述几何体
1.2017·金华一个几何体的三视图如图3-3-1所示,这个几何体是( )
A.球 B.圆柱 C.圆锥 D.立方体
图3-3-1
图3-3-2
2.一个几何体的三视图如图3-3-2所示,则这个几何体是( )
A.圆锥 B.长方体 C.圆柱 D.球
3.如图3-3-3是某个几何体的三视图,该几何体是( )
A.三棱柱 B.三棱锥 C.圆柱 D.圆锥
图3-3-3
图3-3-4
4.某几何体的三视图如图3-3-4所示,这个几何体是( )
A.圆锥 B.圆柱
C.三棱柱 D.三棱锥
图3-3-5
5.如图3-3-5是由三个相同的小正方体组成的几何体的主视图,那么这个几何体可以是( )
图3-3-6
知识点2 与三视图相关的计算问题
图3-3-7
6.由6个大小相同的正方体塔成的几何体如图3-3-7所示,比较它的主视图、左视图和俯视图的面积,则( )
A.三个视图的面积一样大
B.主视图的面积最小
C.左视图的面积最小
D.俯视图的面积最小
7.一个长方体的三视图如图3-3-8所示,则这个长方体的体积为( )
A.30 B.15 C.45 D.20
图3-3-8
图3-3-9
8.由若干个相同的小正方体组合而成的一个几何体的三视图如图3-3-9所示,则组成这个几何体的小正方体的个数是( )
A.4 B.5 C.6 D.9
图3-3-10
9.如图3-3-10是由若干个棱长为1的小正方体组合而成的一个几何体的三视图,则这个几何体的表面积是________.
10.2017·崇仁校级月考如图3-3-11所示的是某个几何体的三视图.
(1)说出这个立体图形的名称;
(2)根据图中的有关数据,求这个几何体的表面积和体积.
图3-3-11
11.图3-3-12是一个几何体的三视图,则这个几何体是( )
图3-3-12
图3-3-13
12.一个几何体是由一些大小相同的小立方块摆成的,其主视图和俯视图如图3-3-14所示,则组成这个几何体的小立方块最少有( )
A.3个 B.4个
C.5个 D.6个
图3-3-14
图3-3-15
13.一个几何体的主视图和俯视图如图3-3-15所示,若这个几何体最多有a个小正方体组成,最少有b个小正方体组成,则a+b的值为( )
A.10 B.11 C.12 D.13
14.如图3-3-16是某几何体的三视图,则该几何体的体积是( )
图3-3-16
A.18 B.54
C.108 D.216
15.如图3-3-17所示的三棱柱的三视图如图3-3-18所示,△EFG中,EF=8 cm,EG=12 cm,∠EGF=30°,则AB的长为________cm.
图3-3-17
图3-3-18
16.几何体的三视图相互关联.某直三棱柱的三视图如图3-3-19所示,在△PMN中,∠MPN=90°,PN=4,sin∠PMN=.
(1)求BC及FG的长;
(2)若主视图与左视图两矩形相似,求AB的长;
(3)在(2)的情况下,求直三棱柱的表面积.
图3-3-19
17.已知一个模型的三视图如图3-3-20所示(单位:m).
(1)请描述这个模型的形状;
(2)若制作这个模型的木料密度为360 kg/m3,则这个模型的质量是多少?
(3)如果用油漆漆这个模型,每千克油漆可以漆4 m2,那么需要多少千克油漆?
图3-3-20
详解详析
1.B
2.B [解析] 观察发现,主视图、左视图、俯视图都是矩形,可以确定几何体是直棱柱,所以这个几何体是长方体,故选B.
3.A 4.A 5.A
6.C [解析] 分别画出这个几何体的主视图、左视图和俯视图,假设每个正方体的棱长为1,则主视图的面积为5,左视图的面积为3,俯视图的面积为4,所以左视图的面积最小.故选C.
7.A 8.A
9.22 [解析] 由俯视图可知左下角的两个位置没有摆放正方体,再结合主视图和左视图得到如图,其中方框里的数字表示在这个位置所摆放的小正方体的个数.
10.解:(1)根据三视图可得:这个立体图形是三棱柱.
(2)这个几何体的表面积为×3×4×2+15×3+15×4+15×5=192;
体积是×3×4×15=90.
11.B [解析] 由主视图易知,只有B选项符合.
12.B [解析] 根据主视图与俯视图可得,此几何体共两层,第一层分前后两排,前一排共有2个立方块,后一排有1个立方块;第二层最少有1个立方块,因此最少有4个,故选B.
13.C [解析] 根据主视图可知俯视图中第一列最高为3个,第二列最高为1个,
∴a=3×2+1=7,b=3+1+1=5,
∴a+b=7+5=12.
14.C [解析] 由三视图可以看出:该几何体是一个正六棱柱,其中底面正六边形的边长为6,高是2,∴该几何体的体积为6××6×6××2=108 .
15.6
16.解:(1)设Rt△PMN斜边上的高为h,由图可知:
BC=MN,FG=h,
∵sin∠PMN=,PN=4,
∴MN=5,PM=3,
∴BC=5.
∵PM·PN=h·MN.
∴h=,
∴FG=.
(2)∵矩形ABCD与矩形EFGH相似,且AB=EF,∴=,
即=,∴AB=2 (负值已舍).
(3)直三棱柱的表面积为×3×4×2+5×2 +3×2 +4×2 =12+24 .
17.解:(1)此模型由两个长方体组成:上面的是小长方体,下面的是大长方体.
(2)模型的体积=3×6×6+2.5×2.5×2=120.5(m3),模型的质量=120.5×360=43380(kg).
(3)模型的表面积=2×2.5×2.5+2×2×2.5+2×6×3+2×3×6+2×6×6=166.5(m2),
需要油漆:166.5÷4=41.625(kg).
