浙教版数学九下 3.4 简单几何体的表面展开图 同步练习(4课时,含答案)
文档属性
| 名称 | 浙教版数学九下 3.4 简单几何体的表面展开图 同步练习(4课时,含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 898.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 18:04:28 | ||
图片预览


文档简介
3.4 简单几何体的表面展开图
第1课时 长方体的表面展开图
知识点.由平面展开图制作立体模型
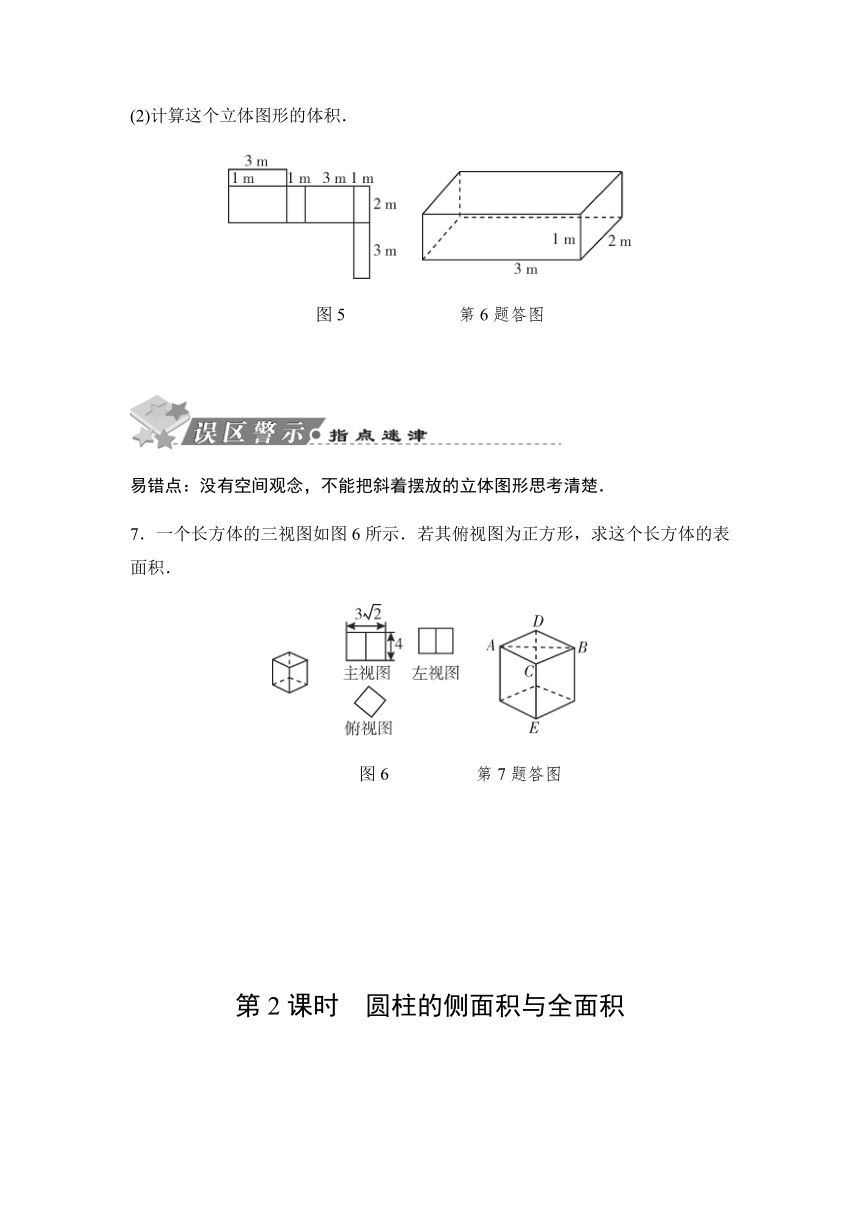
1.下列图形中,可以是正方形表面展开图的是( )
A B C D
2.如图1是某长方体形状包装盒的表面展开图,根据图中的数据,该包装盒的容积是(包装盒材料的厚度忽略不计)( )
A.40×70×80 B.80×80×40
C.40×40×70 D.70×70×80
图1 图2
3.如图2所示的立方体,如果把它展开,可以是下列图形中的( )
A B C D
4.图3①是由白色纸板拼成的立体图形,将它的两个面的外表面涂上颜色,如图②.则下列图形中,是图②的表面展开图的是( )
图3
A B
C D
5.从正面和左面看到的长方体的图形如图4所示(单位:cm),则从其上面看到的图形面积是__ _cm2.
图4
6.如图5所示是一张裁剪好的铁皮,利用这张铁皮可以折叠成一个立体图形.
(1)写出这个立体图形的名称,并画出草图,在草图上标出各部分的长度;
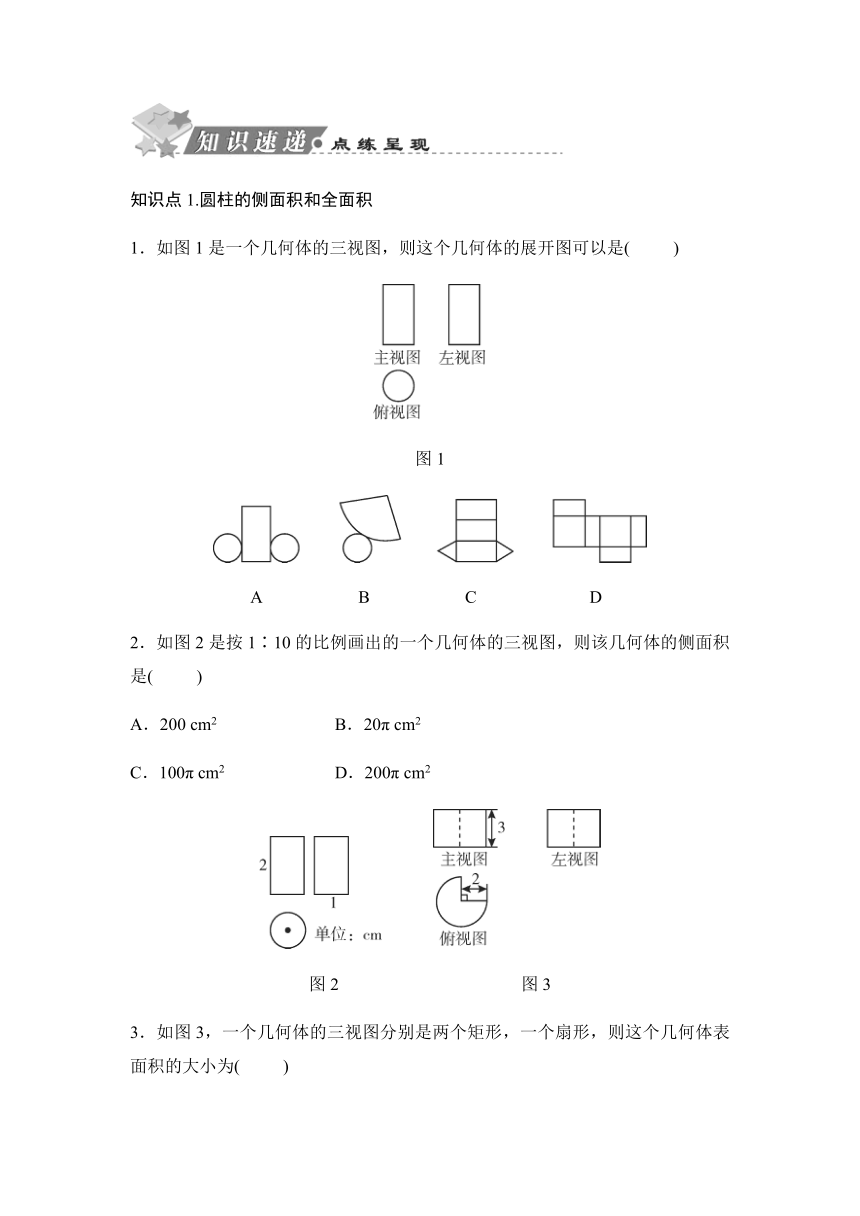
(2)计算这个立体图形的体积.
图5 第6题答图
易错点:没有空间观念,不能把斜着摆放的立体图形思考清楚.
7.一个长方体的三视图如图6所示.若其俯视图为正方形,求这个长方体的表面积.
图6 第7题答图
第2课时 圆柱的侧面积与全面积
知识点1.圆柱的侧面积和全面积
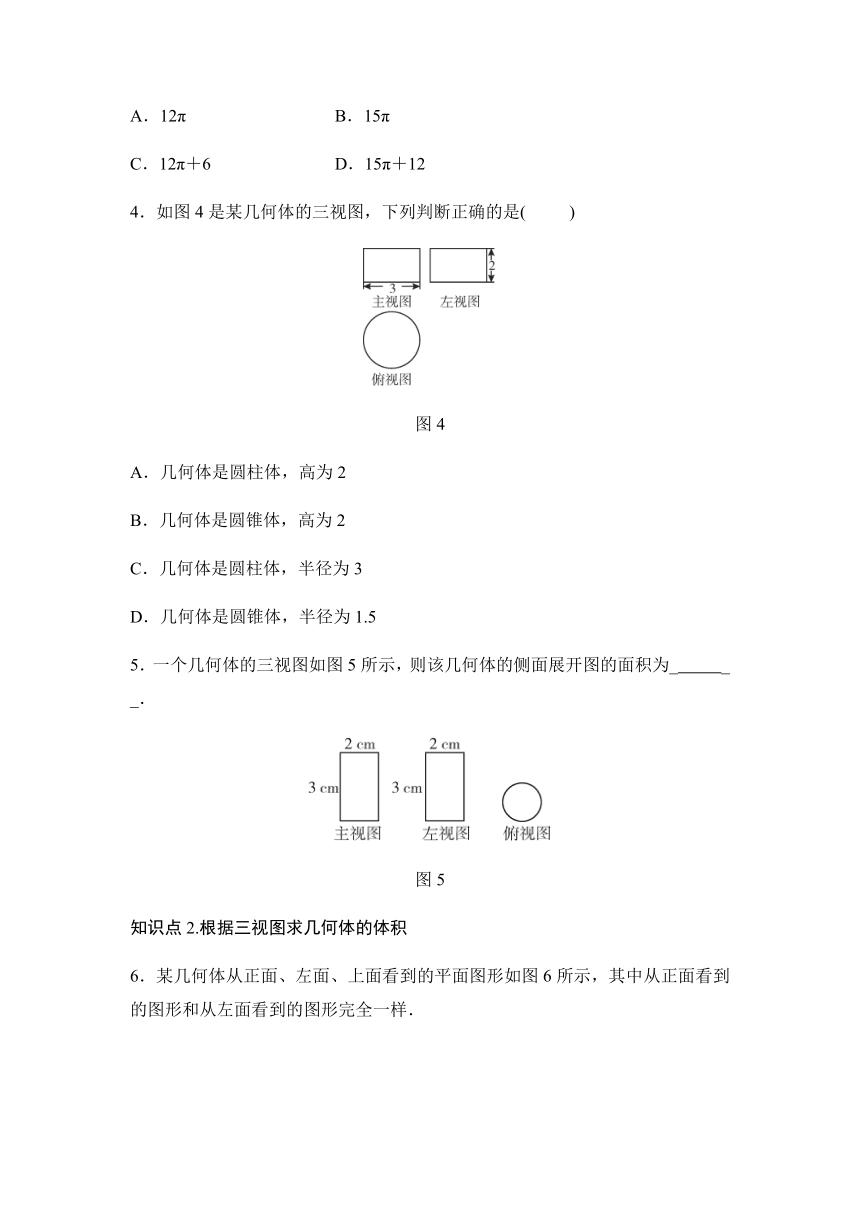
1.如图1是一个几何体的三视图,则这个几何体的展开图可以是( )
图1
A B C D
2.如图2是按1∶10的比例画出的一个几何体的三视图,则该几何体的侧面积是( )
A.200 cm2 B.20π cm2
C.100π cm2 D.200π cm2
图2 图3
3.如图3,一个几何体的三视图分别是两个矩形,一个扇形,则这个几何体表面积的大小为( )
A.12π B.15π
C.12π+6 D.15π+12
4.如图4是某几何体的三视图,下列判断正确的是( )
图4
A.几何体是圆柱体,高为2
B.几何体是圆锥体,高为2
C.几何体是圆柱体,半径为3
D.几何体是圆锥体,半径为1.5
5.一个几何体的三视图如图5所示,则该几何体的侧面展开图的面积为_ _ _.
图5
知识点2.根据三视图求几何体的体积
6.某几何体从正面、左面、上面看到的平面图形如图6所示,其中从正面看到的图形和从左面看到的图形完全一样.
图6
(1)求该几何体的侧面面积(结果保留π);
(2)求该几何体的体积(结果保留π).
易错点:在根据三视图求物体的表面积或体积时,不善于将其转化为立体图形,并进一步转化为平面展开图.
7.如图7是一个圆柱体的三视图,由图中数据计算此圆柱体的全面积为___.(结果保留π)
图7
第3课时 圆锥的侧面积与全面积
知识点.圆锥的侧面积和全面积
1.已知圆锥的底面半径为4 cm,母线长为6 cm,则它的侧面展开图的面积等于( )
A.24 cm2 B.48 cm2
C.24π cm2 D.12π cm2
2.如图1,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱冒(接缝忽略不计),圆锥底面圆的直径是60 cm,则这块扇形铁皮的半径是( )
图1
A.40 cm B.50 cm
C.60 cm D.80 cm
3.如图2,用一个半径为 30 cm,面积为 300π cm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为( )
图2
A.5 cm B.10 cm
C.20 cm D.5π cm
4.已知圆锥的母线长是12,它的侧面展开图的圆心角是120°,则它的底面圆的直径为( )
A.2 B.4
C.6 D.8
5.若一个圆锥的底面圆半径为3,其侧面展开图的圆心角为120°,则圆锥的母线长为____.
6.如图3所示,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12 cm,OA=13 cm,则扇形AOC中的长是____cm.(结果保留π)
图3
7.如图4是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据计算这个几何体的表面积为____cm2.
图4
8.如图5,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2 cm,扇形的圆心角θ=120°,求该圆锥的高h的长.
图5
9.如图6,在Rt△ABC中,∠ACB=90°,AC=BC=2.
(1)如图①,若把Rt△ABC绕边AC所在直线旋转一周,求所得几何体的表面积;
(2)如图②,若绕边AB所在直线旋转一周,则所得几何体的表面积是多少?
图6
易错点:混淆圆锥底面圆的半径和展开图的半径.
10.如图7,有一圆心角为90°,半径长为4 cm的扇形,若将OA,OB重合后围成一圆锥侧面,那么圆锥的高是( )
图7
A. B.2
C.2 D.3
3.4 简单几何体的表面展开图
第1课时 长方体的表面展开图
知识点.由平面展开图制作立体模型
1.下列图形中,可以是正方形表面展开图的是( D )
A B C D
2.如图1是某长方体形状包装盒的表面展开图,根据图中的数据,该包装盒的容积是(包装盒材料的厚度忽略不计)( A )
A.40×70×80 B.80×80×40
C.40×40×70 D.70×70×80
图1 图2
3.如图2所示的立方体,如果把它展开,可以是下列图形中的( D )
A B C D
4.图3①是由白色纸板拼成的立体图形,将它的两个面的外表面涂上颜色,如图②.则下列图形中,是图②的表面展开图的是( B )
图3
A B
C D
5.从正面和左面看到的长方体的图形如图4所示(单位:cm),则从其上面看到的图形面积是__12__cm2.
图4
【解析】 根据从左面、从正面看到的形状图的相关数据可知从上面看到的形状图是长为4宽为3的长方形,其面积是4×3=12(cm2).
6.如图5所示是一张裁剪好的铁皮,利用这张铁皮可以折叠成一个立体图形.
(1)写出这个立体图形的名称,并画出草图,在草图上标出各部分的长度;
(2)计算这个立体图形的体积.
图5 第6题答图
解:(1)长方体,如答图;
(2)该长方体的体积为3×2×1=6(m3).
易错点:没有空间观念,不能把斜着摆放的立体图形思考清楚.
7.一个长方体的三视图如图6所示.若其俯视图为正方形,求这个长方体的表面积.
图6 第7题答图
解:如答图,AB=3,∵AC2+BC2=AB2,∴AC=BC=3,
∴正方形ACBD面积为3×3=9,侧面积为4AC×CE=4×3×4=48,
故这个长方体的表面积为48+9+9=66.
第2课时 圆柱的侧面积与全面积
知识点1.圆柱的侧面积和全面积
1.如图1是一个几何体的三视图,则这个几何体的展开图可以是( A )
图1
A B C D
2.如图2是按1∶10的比例画出的一个几何体的三视图,则该几何体的侧面积是( D )
A.200 cm2 B.20π cm2
C.100π cm2 D.200π cm2
【解析】 观察三视图知该几何体为圆柱,根据1∶10的比例可知其高为20,底面直径为10,∴原几何体的侧面积=πdh=π×10×20=200π.
图2 图3
3.如图3,一个几何体的三视图分别是两个矩形,一个扇形,则这个几何体表面积的大小为( D )
A.12π B.15π
C.12π+6 D.15π+12
【解析】 由几何体的三视图可知该几何体的表面是由3个长方形与两个扇形围成,故几何体表面积为2×3×2+×2π×2×3+2×π×22=15π+12.
4.如图4是某几何体的三视图,下列判断正确的是( A )
图4
A.几何体是圆柱体,高为2
B.几何体是圆锥体,高为2
C.几何体是圆柱体,半径为3
D.几何体是圆锥体,半径为1.5
【解析】 观察该几何体可知,该几何体的主视图与左视图均为长为3,宽为2的长方形,俯视图为圆,从而确定该几何体是高为2,直径为3的圆柱体.
5.一个几何体的三视图如图5所示,则该几何体的侧面展开图的面积为__6π__cm2__.
图5
【解析】 由三视图可得此几何体为圆柱,故侧面积=π×2×3=6π cm2.
知识点2.根据三视图求几何体的体积
6.[2018秋·沙坪坝区校级期中]某几何体从正面、左面、上面看到的平面图形如图6所示,其中从正面看到的图形和从左面看到的图形完全一样.
图6
(1)求该几何体的侧面面积(结果保留π);
(2)求该几何体的体积(结果保留π).
解:(1)由三视图知该几何体是底面直径为6,高为8的圆柱体,
∴该几何体的侧面面积为π×6×8=48π;
(2)此圆柱体的体积为π××8=72π.
易错点:在根据三视图求物体的表面积或体积时,不善于将其转化为立体图形,并进一步转化为平面展开图.
7.如图7是一个圆柱体的三视图,由图中数据计算此圆柱体的全面积为__32π__.(结果保留π)
图7
【解析】 由图可知,圆柱体的底面直径为4,高为6,故全面积=4×π×6+2×π×22=32π.
第3课时 圆锥的侧面积与全面积
知识点.圆锥的侧面积和全面积
1.已知圆锥的底面半径为4 cm,母线长为6 cm,则它的侧面展开图的面积等于( C )
A.24 cm2 B.48 cm2
C.24π cm2 D.12π cm2
2.如图1,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱冒(接缝忽略不计),圆锥底面圆的直径是60 cm,则这块扇形铁皮的半径是( A )
图1
A.40 cm B.50 cm
C.60 cm D.80 cm
【解析】 ∵圆锥的底面直径为60 cm,∴圆锥的底面周长为60π cm,∴扇形的弧长为60π cm,设扇形的半径为r,则=60π,解得r=40 cm.
3.如图2,用一个半径为 30 cm,面积为 300π cm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为( B )
图2
A.5 cm B.10 cm
C.20 cm D.5π cm
4.已知圆锥的母线长是12,它的侧面展开图的圆心角是120°,则它的底面圆的直径为( D )
A.2 B.4
C.6 D.8
5.若一个圆锥的底面圆半径为3,其侧面展开图的圆心角为120°,则圆锥的母线长为__9__.
【解析】 设母线长为l,则120=·360,解得l=9.
6.如图3所示,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12 cm,OA=13 cm,则扇形AOC中的长是__10π__cm.(结果保留π)
图3
【解析】 ∵圆锥的高h为12 cm,OA=13 cm,∴圆锥的底面半径为=5 cm,∴圆锥的底面周长为10π cm,∴扇形AOC中的长是10π cm.
7.如图4是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据计算这个几何体的表面积为__4π__cm2.
图4
【解析】 由三视图可判断出这个几何体是圆锥;根据三视图知该圆锥的母线长为3 cm,底面半径为1 cm,故表面积=πrl+πr2=π×1×3+π×12=4π cm2.
8.如图5,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2 cm,扇形的圆心角θ=120°,求该圆锥的高h的长.
图5
解:由题意得120=·360,解得l=6 cm,∴由勾股定理得h==4 cm.
9.如图6,在Rt△ABC中,∠ACB=90°,AC=BC=2.
(1)如图①,若把Rt△ABC绕边AC所在直线旋转一周,求所得几何体的表面积;
(2)如图②,若绕边AB所在直线旋转一周,则所得几何体的表面积是多少?
图6
解:(1)∵在Rt△ABC中,∠ACB=90°,AC=BC=2,
∴BA2=CB2+AC2=16,∴AB=4,
旋转得到的圆锥的侧面积=π×2×4=8π,底面面积=π×(2)2=8π,
则所得几何体的表面积为(8+8)π;
(2)由题意得所得圆锥底面半径为2,
∴该几何体的表面积=2×π×2×2=8π.
易错点:混淆圆锥底面圆的半径和展开图的半径.
10.如图7,有一圆心角为90°,半径长为4 cm的扇形,若将OA,OB重合后围成一圆锥侧面,那么圆锥的高是( A )
图7
A. B.2
C.2 D.3
【解析】 由90=·360,得底面圆半径为1,已知OA=4,由勾股定理得圆锥的高是=
第1课时 长方体的表面展开图
知识点.由平面展开图制作立体模型
1.下列图形中,可以是正方形表面展开图的是( )
A B C D
2.如图1是某长方体形状包装盒的表面展开图,根据图中的数据,该包装盒的容积是(包装盒材料的厚度忽略不计)( )
A.40×70×80 B.80×80×40
C.40×40×70 D.70×70×80
图1 图2
3.如图2所示的立方体,如果把它展开,可以是下列图形中的( )
A B C D
4.图3①是由白色纸板拼成的立体图形,将它的两个面的外表面涂上颜色,如图②.则下列图形中,是图②的表面展开图的是( )
图3
A B
C D
5.从正面和左面看到的长方体的图形如图4所示(单位:cm),则从其上面看到的图形面积是__ _cm2.
图4
6.如图5所示是一张裁剪好的铁皮,利用这张铁皮可以折叠成一个立体图形.
(1)写出这个立体图形的名称,并画出草图,在草图上标出各部分的长度;
(2)计算这个立体图形的体积.
图5 第6题答图
易错点:没有空间观念,不能把斜着摆放的立体图形思考清楚.
7.一个长方体的三视图如图6所示.若其俯视图为正方形,求这个长方体的表面积.
图6 第7题答图
第2课时 圆柱的侧面积与全面积
知识点1.圆柱的侧面积和全面积
1.如图1是一个几何体的三视图,则这个几何体的展开图可以是( )
图1
A B C D
2.如图2是按1∶10的比例画出的一个几何体的三视图,则该几何体的侧面积是( )
A.200 cm2 B.20π cm2
C.100π cm2 D.200π cm2
图2 图3
3.如图3,一个几何体的三视图分别是两个矩形,一个扇形,则这个几何体表面积的大小为( )
A.12π B.15π
C.12π+6 D.15π+12
4.如图4是某几何体的三视图,下列判断正确的是( )
图4
A.几何体是圆柱体,高为2
B.几何体是圆锥体,高为2
C.几何体是圆柱体,半径为3
D.几何体是圆锥体,半径为1.5
5.一个几何体的三视图如图5所示,则该几何体的侧面展开图的面积为_ _ _.
图5
知识点2.根据三视图求几何体的体积
6.某几何体从正面、左面、上面看到的平面图形如图6所示,其中从正面看到的图形和从左面看到的图形完全一样.
图6
(1)求该几何体的侧面面积(结果保留π);
(2)求该几何体的体积(结果保留π).
易错点:在根据三视图求物体的表面积或体积时,不善于将其转化为立体图形,并进一步转化为平面展开图.
7.如图7是一个圆柱体的三视图,由图中数据计算此圆柱体的全面积为___.(结果保留π)
图7
第3课时 圆锥的侧面积与全面积
知识点.圆锥的侧面积和全面积
1.已知圆锥的底面半径为4 cm,母线长为6 cm,则它的侧面展开图的面积等于( )
A.24 cm2 B.48 cm2
C.24π cm2 D.12π cm2
2.如图1,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱冒(接缝忽略不计),圆锥底面圆的直径是60 cm,则这块扇形铁皮的半径是( )
图1
A.40 cm B.50 cm
C.60 cm D.80 cm
3.如图2,用一个半径为 30 cm,面积为 300π cm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为( )
图2
A.5 cm B.10 cm
C.20 cm D.5π cm
4.已知圆锥的母线长是12,它的侧面展开图的圆心角是120°,则它的底面圆的直径为( )
A.2 B.4
C.6 D.8
5.若一个圆锥的底面圆半径为3,其侧面展开图的圆心角为120°,则圆锥的母线长为____.
6.如图3所示,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12 cm,OA=13 cm,则扇形AOC中的长是____cm.(结果保留π)
图3
7.如图4是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据计算这个几何体的表面积为____cm2.
图4
8.如图5,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2 cm,扇形的圆心角θ=120°,求该圆锥的高h的长.
图5
9.如图6,在Rt△ABC中,∠ACB=90°,AC=BC=2.
(1)如图①,若把Rt△ABC绕边AC所在直线旋转一周,求所得几何体的表面积;
(2)如图②,若绕边AB所在直线旋转一周,则所得几何体的表面积是多少?
图6
易错点:混淆圆锥底面圆的半径和展开图的半径.
10.如图7,有一圆心角为90°,半径长为4 cm的扇形,若将OA,OB重合后围成一圆锥侧面,那么圆锥的高是( )
图7
A. B.2
C.2 D.3
3.4 简单几何体的表面展开图
第1课时 长方体的表面展开图
知识点.由平面展开图制作立体模型
1.下列图形中,可以是正方形表面展开图的是( D )
A B C D
2.如图1是某长方体形状包装盒的表面展开图,根据图中的数据,该包装盒的容积是(包装盒材料的厚度忽略不计)( A )
A.40×70×80 B.80×80×40
C.40×40×70 D.70×70×80
图1 图2
3.如图2所示的立方体,如果把它展开,可以是下列图形中的( D )
A B C D
4.图3①是由白色纸板拼成的立体图形,将它的两个面的外表面涂上颜色,如图②.则下列图形中,是图②的表面展开图的是( B )
图3
A B
C D
5.从正面和左面看到的长方体的图形如图4所示(单位:cm),则从其上面看到的图形面积是__12__cm2.
图4
【解析】 根据从左面、从正面看到的形状图的相关数据可知从上面看到的形状图是长为4宽为3的长方形,其面积是4×3=12(cm2).
6.如图5所示是一张裁剪好的铁皮,利用这张铁皮可以折叠成一个立体图形.
(1)写出这个立体图形的名称,并画出草图,在草图上标出各部分的长度;
(2)计算这个立体图形的体积.
图5 第6题答图
解:(1)长方体,如答图;
(2)该长方体的体积为3×2×1=6(m3).
易错点:没有空间观念,不能把斜着摆放的立体图形思考清楚.
7.一个长方体的三视图如图6所示.若其俯视图为正方形,求这个长方体的表面积.
图6 第7题答图
解:如答图,AB=3,∵AC2+BC2=AB2,∴AC=BC=3,
∴正方形ACBD面积为3×3=9,侧面积为4AC×CE=4×3×4=48,
故这个长方体的表面积为48+9+9=66.
第2课时 圆柱的侧面积与全面积
知识点1.圆柱的侧面积和全面积
1.如图1是一个几何体的三视图,则这个几何体的展开图可以是( A )
图1
A B C D
2.如图2是按1∶10的比例画出的一个几何体的三视图,则该几何体的侧面积是( D )
A.200 cm2 B.20π cm2
C.100π cm2 D.200π cm2
【解析】 观察三视图知该几何体为圆柱,根据1∶10的比例可知其高为20,底面直径为10,∴原几何体的侧面积=πdh=π×10×20=200π.
图2 图3
3.如图3,一个几何体的三视图分别是两个矩形,一个扇形,则这个几何体表面积的大小为( D )
A.12π B.15π
C.12π+6 D.15π+12
【解析】 由几何体的三视图可知该几何体的表面是由3个长方形与两个扇形围成,故几何体表面积为2×3×2+×2π×2×3+2×π×22=15π+12.
4.如图4是某几何体的三视图,下列判断正确的是( A )
图4
A.几何体是圆柱体,高为2
B.几何体是圆锥体,高为2
C.几何体是圆柱体,半径为3
D.几何体是圆锥体,半径为1.5
【解析】 观察该几何体可知,该几何体的主视图与左视图均为长为3,宽为2的长方形,俯视图为圆,从而确定该几何体是高为2,直径为3的圆柱体.
5.一个几何体的三视图如图5所示,则该几何体的侧面展开图的面积为__6π__cm2__.
图5
【解析】 由三视图可得此几何体为圆柱,故侧面积=π×2×3=6π cm2.
知识点2.根据三视图求几何体的体积
6.[2018秋·沙坪坝区校级期中]某几何体从正面、左面、上面看到的平面图形如图6所示,其中从正面看到的图形和从左面看到的图形完全一样.
图6
(1)求该几何体的侧面面积(结果保留π);
(2)求该几何体的体积(结果保留π).
解:(1)由三视图知该几何体是底面直径为6,高为8的圆柱体,
∴该几何体的侧面面积为π×6×8=48π;
(2)此圆柱体的体积为π××8=72π.
易错点:在根据三视图求物体的表面积或体积时,不善于将其转化为立体图形,并进一步转化为平面展开图.
7.如图7是一个圆柱体的三视图,由图中数据计算此圆柱体的全面积为__32π__.(结果保留π)
图7
【解析】 由图可知,圆柱体的底面直径为4,高为6,故全面积=4×π×6+2×π×22=32π.
第3课时 圆锥的侧面积与全面积
知识点.圆锥的侧面积和全面积
1.已知圆锥的底面半径为4 cm,母线长为6 cm,则它的侧面展开图的面积等于( C )
A.24 cm2 B.48 cm2
C.24π cm2 D.12π cm2
2.如图1,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱冒(接缝忽略不计),圆锥底面圆的直径是60 cm,则这块扇形铁皮的半径是( A )
图1
A.40 cm B.50 cm
C.60 cm D.80 cm
【解析】 ∵圆锥的底面直径为60 cm,∴圆锥的底面周长为60π cm,∴扇形的弧长为60π cm,设扇形的半径为r,则=60π,解得r=40 cm.
3.如图2,用一个半径为 30 cm,面积为 300π cm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为( B )
图2
A.5 cm B.10 cm
C.20 cm D.5π cm
4.已知圆锥的母线长是12,它的侧面展开图的圆心角是120°,则它的底面圆的直径为( D )
A.2 B.4
C.6 D.8
5.若一个圆锥的底面圆半径为3,其侧面展开图的圆心角为120°,则圆锥的母线长为__9__.
【解析】 设母线长为l,则120=·360,解得l=9.
6.如图3所示,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12 cm,OA=13 cm,则扇形AOC中的长是__10π__cm.(结果保留π)
图3
【解析】 ∵圆锥的高h为12 cm,OA=13 cm,∴圆锥的底面半径为=5 cm,∴圆锥的底面周长为10π cm,∴扇形AOC中的长是10π cm.
7.如图4是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据计算这个几何体的表面积为__4π__cm2.
图4
【解析】 由三视图可判断出这个几何体是圆锥;根据三视图知该圆锥的母线长为3 cm,底面半径为1 cm,故表面积=πrl+πr2=π×1×3+π×12=4π cm2.
8.如图5,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2 cm,扇形的圆心角θ=120°,求该圆锥的高h的长.
图5
解:由题意得120=·360,解得l=6 cm,∴由勾股定理得h==4 cm.
9.如图6,在Rt△ABC中,∠ACB=90°,AC=BC=2.
(1)如图①,若把Rt△ABC绕边AC所在直线旋转一周,求所得几何体的表面积;
(2)如图②,若绕边AB所在直线旋转一周,则所得几何体的表面积是多少?
图6
解:(1)∵在Rt△ABC中,∠ACB=90°,AC=BC=2,
∴BA2=CB2+AC2=16,∴AB=4,
旋转得到的圆锥的侧面积=π×2×4=8π,底面面积=π×(2)2=8π,
则所得几何体的表面积为(8+8)π;
(2)由题意得所得圆锥底面半径为2,
∴该几何体的表面积=2×π×2×2=8π.
易错点:混淆圆锥底面圆的半径和展开图的半径.
10.如图7,有一圆心角为90°,半径长为4 cm的扇形,若将OA,OB重合后围成一圆锥侧面,那么圆锥的高是( A )
图7
A. B.2
C.2 D.3
【解析】 由90=·360,得底面圆半径为1,已知OA=4,由勾股定理得圆锥的高是=
