2021-2022学年浙教版八年级数学下册第3章数据分析初步同步练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年浙教版八年级数学下册第3章数据分析初步同步练习题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 147.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-12 20:29:07 | ||
图片预览



文档简介
2021-2022学年浙教版八年级数学下册《第3章数据分析初步》同步练习题(附答案)
一.选择题
1.气象局调查了甲、乙、丙、丁四个城市连续四年的降水量,它们的平均降水量都是320毫米,方差分别是S=3.2,S=5.2,S=7.3,S=3.1,则这四个城市年降水量最稳定的是( )
A.甲 B.乙 C.丙 D.丁
2.甲、乙两队参加中国汉字听写大会比赛,两队各10人,比赛成绩总分10分)统计如表:
甲 8 9 7 10 7 10 9 10 10 9
乙 8 7 10 8 9 10 10 9 10 10
根据表格中的信息,判断下列结论正确的是( )
A.甲队成绩的中位数是9.5分
B.乙队成绩的众数是10分
C.甲队的成绩比较稳定
D.乙队的平均成绩是9分
3.一个样本的每一个数据都减少3,其统计量不变的是( )
A.平均数 B.中位数 C.众数 D.方差
4.在一次献爱心的捐款活动中,八(2)班50名同学捐款金额如图所示,则在这次捐款活动中,该班同学捐款金额的众数和中位数分别是( )
A.20,10 B.10,20 C.10,10 D.10,15
5.下表中记录了甲、乙、丙、丁四名同学参加金钥匙选拔赛成绩的平均分和方差.要从中选择一名成绩较好且发挥稳定的同学去海安市参加决赛,最合适的同学是( )
甲 乙 丙 丁
平均分 90 87 90 87
方差S2 12.5 13.5 1.4 1.4
A.甲 B.乙 C.丙 D.丁
6.某单位招聘一名员工,从专业知识、工作业绩、面试成绩三个方面进行考核(考核的满分均为100分),三个方面的权重比依次为2:4:4.小明经过考核后所得的分数依次为90,85,80分,那么小明考核的最后得分是( )
A.80 B.84 C.87 D.90
7.小天计算一组数据92,90,94,86,100,88的方差为S02,则数据46,45,47,43,50,44的方差为( )
A. B. C. D.
8.中考体育测试前,某校为了了解选报引体向上的九年级男生的成绩情况,随机抽测了部分九年级男生引体向上的成绩,并将测试的成绩制成了如下的统计表:
个数 13 14 15 16
人数 3 5 1 1
依据如表提供的信息,下列判断正确的是( )
A.众数是5 B.中位数是14.5
C.平均数是14 D.方差是8
二.填空题
9.一组数据4,3,6,x的平均数是4,则这组数据的方差是 .
10.在5个正整数a、b、c、d、e中,中位数是4,唯一的众数是6,则这5个数的和最大值是 .
11.已知一组数据x1,x2,x3,方差是2,那么另一组数据2x1﹣4,2x2﹣4,2x3﹣4的方差是 .
12.每千克x元的糖果a千克和每千克y元的糖果b千克混合后,要求总价额不变,那么混合糖果的售价定为每千克 元.
13.为了落实教育部提出的“双减政策”,历下区各学校积极研发个性化、可选择的数学作业.一天,小明对他学习小组其他三位同学完成数学作业的时间进行了调查,得到的结果分别为:18分钟,20分钟,25分钟.然后他告诉大家说,我们四个人完成数学作业的平均时间是21分钟.请问小明同学完成数学作业的时间是 分钟.
14.在从小到大排列的五个数x,3,6,8,12中再加入一个数,若这六个数的中位数、平均数与原来五个数的中位数、平均数分别相等,则加入的这个数为 ,x的值为 .
15.一次测试,某6人小组有一人得85分,有两人得88分,有三人得91分,则这个小组学生的平均得分是 .
16.已知1,2,3,4,5的方差为2,则2021,2022,2023,2024,2025的方差为 .
三.解答题
17.某学校从九年级同学中任意选取40人,随机分成甲、乙两个小组进行“引体向上”体能测试,根据测试成绩绘制出统计表和如图所示的统计图(成绩均为整数,满分为10分)
甲组成绩统计表:
成绩 7 8 9 10
人数 1 9 5 5
根据上面的信息,解答下列问题:
(1)甲组的平均成绩为 分,m= ,甲组成绩的中位数是 ,乙组成绩的众数是 ;
(2)若已经计算出甲组成绩方差为0.81,求出乙组成绩的方差,并判断哪个小组的成绩更加稳定?
18.某校对初一年级三个班级的教室卫生情况进行如下考核:黑板、门窗、桌椅、地面.这一周三个班的各项卫生成绩(单位:分)分别如下表:
黑板 门窗 桌椅 地面
(1)班 95 90 95 95
(2)班 90 92 85 90
(3)班 85 90 90 90
总评时将黑板、门窗、桌椅、地面这四项得分按15%,10%,35%,40%的比例计算各班的卫生成绩,哪个班的成绩最高?
19.为提高中学生网络安全意识,我县某中学特举办“网络安全知识答题竞赛”,八年级(1)、(2)班根据初赛成绩各选出5名选手代表各班参加学校决赛,两个班各选出的5名选手的决赛成绩(单位:分)如下:
八年级(1)班:75 80 85 85 100
八年级(2)班:70 100 100 75 80
分析数据如下表所示:
平均数(分) 中位数(分) 众数(分) 方差(分2)
八年级(1)班 a 85 b 70
八年级(2)班 85 c 100 160
(1)上表中的a,b,c分别是多少?
(2)分析两个班的平均数和方差,你认为哪个班的决赛成绩较好?为什么?
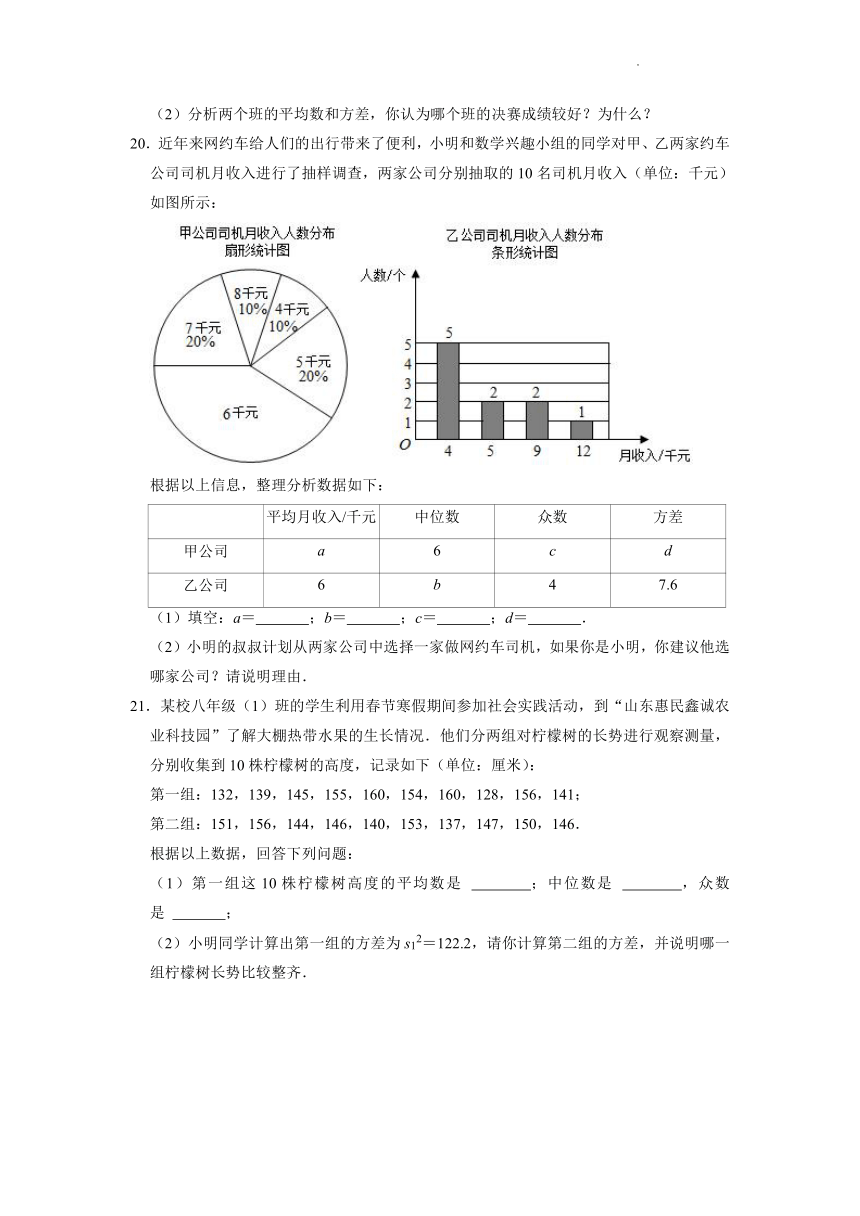
20.近年来网约车给人们的出行带来了便利,小明和数学兴趣小组的同学对甲、乙两家约车公司司机月收入进行了抽样调查,两家公司分别抽取的10名司机月收入(单位:千元)如图所示:
根据以上信息,整理分析数据如下:
平均月收入/千元 中位数 众数 方差
甲公司 a 6 c d
乙公司 6 b 4 7.6
(1)填空:a= ;b= ;c= ;d= .
(2)小明的叔叔计划从两家公司中选择一家做网约车司机,如果你是小明,你建议他选哪家公司?请说明理由.
21.某校八年级(1)班的学生利用春节寒假期间参加社会实践活动,到“山东惠民鑫诚农业科技园”了解大棚热带水果的生长情况.他们分两组对柠檬树的长势进行观察测量,分别收集到10株柠檬树的高度,记录如下(单位:厘米):
第一组:132,139,145,155,160,154,160,128,156,141;
第二组:151,156,144,146,140,153,137,147,150,146.
根据以上数据,回答下列问题:
(1)第一组这10株柠檬树高度的平均数是 ;中位数是 ,众数是 ;
(2)小明同学计算出第一组的方差为s12=122.2,请你计算第二组的方差,并说明哪一组柠檬树长势比较整齐.
参考答案
一.选择题
1.解:∵S=3.2,S=5.2,S=7.3,S=3.1,
∴S<S<S<S,
∴这四个城市年降水量最稳定的是丁,
故选:D.
2.解:A.甲队数据重新排列为7、7、8、9、9、9、10、10、10、10,所以甲队数据的中位数是=9(分),此选项错误;
B.乙队成绩的众数是10分,此选项正确;
C.∵==8.9,==9.1,
∴=×[2×(7﹣8.9)2+(8﹣8.9)2+3×(9﹣8.9)2+4×(10﹣8.9)2]=1.29,
=×[(7﹣9.1)2+2×(8﹣9.1)2+2×(9﹣9.1)2+5×(10﹣9.1)2]=1.09,
∴<,
∴乙队的成绩比较稳定,此选项错误;
D.由C选项知乙队的平均成绩是9.1分,此选项错误;
故选:B.
3.解:∵一个样本的每一个数据都减少3,样本数据的波动幅度不会发生变化,
∴统计量不变的是方差,
故选:D.
4.解:这组数据的中位数是第25、26个数据的平均数,由条形统计图知第25、26个数据分别为10、10,
所以这组数据的中位数为=10(元),
这组数据中出现次数最多的是10元,有20次,
所以这组数据的众数为10元,
故选:C.
5.解:∵乙和丁的平均数最小,
∴从甲和丙中选择一人参加比赛,
∵丙的方差最小,
∴选择丙参赛.
故选:C.
6.解:小明考核的最后得分为=84(分),
故选:B.
7.解:原数据重新排列为86,88,90,92,94,100,
新数据重新排列为43,44,45,46,47,50,
所以新数据是将原数据分别乘所得,
∵原数据的方差为S02,
∴新数据的方差为()2×S02=S02,
故选:C.
8.解:这组数据中出现次数最多的是14,出现5次,
所以这组数据的众数是14,故A选项错误;
中位数是=14(个),故B选项错误;
平均数为=14(个),故C选项正确;
方差为×[3×(13﹣14)2+5×(14﹣14)2+(15﹣14)2+(16﹣14)2]=0.8,故D选项错误;
故选:C.
二.填空题
9.解:因为数据4,3,6,x的平均数是4,
所以=4,
解得:x=3,
方差为:×[(4 4)2+(3 4)2+(6 4)2+(3 4)2]=,
故答案为:.
10.解:设五个数从小到大为a1,a2,a3,a4,a5,
依题意得a3=4,a4=a5=6,
a1,a2是1,2,3中两个不同的数,
符合题意的五个数可能有三种情形:
“1,2,4,6,6”,“1,3,4,6,6”,“2,3,4,6,6”,
1+2+4+6+6=19,1+3+4+6+6=20,2+3+4+6+6=21,
则这5个数的和最大值是21.
故答案为21.
11.解:∵数据x1,x2,x3,方差是2,
∴数据2x1﹣4,2x2﹣4,2x3﹣4的方差22×2=8.
故答案为:8.
12.解:∵每千克x元的糖果a千克,每千克y元的糖果b千克,
∴混合后共有(a+b)千克,混合糖果共售(ax+by)元,
∴混合糖果的售价定为每千克元.
故答案为:.
13.解:设小明同学完成数学作业的时间是x分钟,
根据题意,得:=21,
解得x=21,
∴小明同学完成数学作业的时间是21分钟,
故答案为:21.
14.解:从小到大排列的五个数x,3,6,8,12的中位数是6,
∵再加入一个数,这六个数的中位数与原来五个数的中位数相等,
∴加入的一个数是6,
∵这六个数的平均数与原来五个数的平均数相等,
∴(x+3+6+8+12)=(x+3+6+6+8+12),
解得x=1.
所以加入的数为6,x=1.
故答案为:6,1.
15.解:这个小组学生的平均得分==89(分),
故答案为:89分.
16.解:∵1,2,3,4,5的方差为2,
∴2021,2022,2023,2024,2025的方差为2,
故答案为:2.
三.解答题
17.解:(1)甲组的平均成绩为×(7×1+8×9+9×5+10×5)=8.7,
由题意可得:1+9+5+5+2+9+6+m=40,解得m=3,
甲组成绩一共有20个,从小到大最中间为8和9,则中位数为=8.5,
乙组成绩中最多的为8,则众数为8,
故答案为:8.7、3、8.5、8;
(2)==8.5,
==0.75,
∵<,
∴乙组的成绩更加稳定.
18.解:(1)班的加权平均成绩是:95×15%+90×10%+95×35%+95×40%=94.5(分),
(2)班的加权平均成绩是:90×15%+92×10%+85×35%+90×40%=88.45(分),
(3)班的加权平均成绩是:85×15%+90×10%+90×35%+90×40%=89.25(分),
∵94.5>89.25>88.45,
∴(1)班的成绩高.
19.解:(1)八年级(1)班成绩的平均数a==85,众数b=85;
将八年级(2)班成绩重新排列为70、75、80、100、100,
∴八年级(1)班成绩的中位数c=80;
(2)八年级(1)班的成绩好.
因为两个班的平均分都是85分,不分上下,而八年级(1)班的方差70小于八年级(2)班的方差160,方差越小越稳定.
所以八年级(1)班的成绩好.
20.解:(1)∵“6千元”对应的百分比为1﹣(10%+20%+10%+20%)=40%,
∴甲公司平均月收入a=4×10%+5×20%+6×40%+7×20%+8×10%=6,
众数c=6,
方差d=[(4﹣6)2+2×(5﹣6)2+4×(6﹣6)2+2×(7﹣6)2+(8﹣6)2]=1.2;
乙公司中位数b==4.5,
故答案为:6;4.5;6;1.2;
(2)选甲公司,理由如下:
因为平均数相同,中位数、众数甲公司均大于乙公司,且甲公司方差小,更稳定,所以选甲公司.
解:(1)第一组这10株柠檬树高度的平均数是
(132+139+145+155+160+154+160+128+156+141)÷10=147(厘米).
把这些数据从小到大排列为128、132、139、141、145、154、155、156、160、160,
最中间的两个数是145和154,则中位数是(145+154)÷2=149.5(厘米).
160出现了2次,出现的次数最多,则众数是160厘米.
故答案为:147厘米,149.5厘米,160厘米;
∵第二组这10株柠檬树高度的平均数是
(151+156+144+146+140+153+137+147+150+146)÷10=147,
∴S22=×[(151﹣147)2+(156﹣147)2+(144﹣147)2+(146﹣147)2+(140﹣147)2+(153﹣147)2+(137﹣147)2+(147﹣147)2+(150﹣147)2+(146﹣147)2]=30.2,
∵S12=122.2>S22,
∴第二组柠檬树长势比较整齐.
一.选择题
1.气象局调查了甲、乙、丙、丁四个城市连续四年的降水量,它们的平均降水量都是320毫米,方差分别是S=3.2,S=5.2,S=7.3,S=3.1,则这四个城市年降水量最稳定的是( )
A.甲 B.乙 C.丙 D.丁
2.甲、乙两队参加中国汉字听写大会比赛,两队各10人,比赛成绩总分10分)统计如表:
甲 8 9 7 10 7 10 9 10 10 9
乙 8 7 10 8 9 10 10 9 10 10
根据表格中的信息,判断下列结论正确的是( )
A.甲队成绩的中位数是9.5分
B.乙队成绩的众数是10分
C.甲队的成绩比较稳定
D.乙队的平均成绩是9分
3.一个样本的每一个数据都减少3,其统计量不变的是( )
A.平均数 B.中位数 C.众数 D.方差
4.在一次献爱心的捐款活动中,八(2)班50名同学捐款金额如图所示,则在这次捐款活动中,该班同学捐款金额的众数和中位数分别是( )
A.20,10 B.10,20 C.10,10 D.10,15
5.下表中记录了甲、乙、丙、丁四名同学参加金钥匙选拔赛成绩的平均分和方差.要从中选择一名成绩较好且发挥稳定的同学去海安市参加决赛,最合适的同学是( )
甲 乙 丙 丁
平均分 90 87 90 87
方差S2 12.5 13.5 1.4 1.4
A.甲 B.乙 C.丙 D.丁
6.某单位招聘一名员工,从专业知识、工作业绩、面试成绩三个方面进行考核(考核的满分均为100分),三个方面的权重比依次为2:4:4.小明经过考核后所得的分数依次为90,85,80分,那么小明考核的最后得分是( )
A.80 B.84 C.87 D.90
7.小天计算一组数据92,90,94,86,100,88的方差为S02,则数据46,45,47,43,50,44的方差为( )
A. B. C. D.
8.中考体育测试前,某校为了了解选报引体向上的九年级男生的成绩情况,随机抽测了部分九年级男生引体向上的成绩,并将测试的成绩制成了如下的统计表:
个数 13 14 15 16
人数 3 5 1 1
依据如表提供的信息,下列判断正确的是( )
A.众数是5 B.中位数是14.5
C.平均数是14 D.方差是8
二.填空题
9.一组数据4,3,6,x的平均数是4,则这组数据的方差是 .
10.在5个正整数a、b、c、d、e中,中位数是4,唯一的众数是6,则这5个数的和最大值是 .
11.已知一组数据x1,x2,x3,方差是2,那么另一组数据2x1﹣4,2x2﹣4,2x3﹣4的方差是 .
12.每千克x元的糖果a千克和每千克y元的糖果b千克混合后,要求总价额不变,那么混合糖果的售价定为每千克 元.
13.为了落实教育部提出的“双减政策”,历下区各学校积极研发个性化、可选择的数学作业.一天,小明对他学习小组其他三位同学完成数学作业的时间进行了调查,得到的结果分别为:18分钟,20分钟,25分钟.然后他告诉大家说,我们四个人完成数学作业的平均时间是21分钟.请问小明同学完成数学作业的时间是 分钟.
14.在从小到大排列的五个数x,3,6,8,12中再加入一个数,若这六个数的中位数、平均数与原来五个数的中位数、平均数分别相等,则加入的这个数为 ,x的值为 .
15.一次测试,某6人小组有一人得85分,有两人得88分,有三人得91分,则这个小组学生的平均得分是 .
16.已知1,2,3,4,5的方差为2,则2021,2022,2023,2024,2025的方差为 .
三.解答题
17.某学校从九年级同学中任意选取40人,随机分成甲、乙两个小组进行“引体向上”体能测试,根据测试成绩绘制出统计表和如图所示的统计图(成绩均为整数,满分为10分)
甲组成绩统计表:
成绩 7 8 9 10
人数 1 9 5 5
根据上面的信息,解答下列问题:
(1)甲组的平均成绩为 分,m= ,甲组成绩的中位数是 ,乙组成绩的众数是 ;
(2)若已经计算出甲组成绩方差为0.81,求出乙组成绩的方差,并判断哪个小组的成绩更加稳定?
18.某校对初一年级三个班级的教室卫生情况进行如下考核:黑板、门窗、桌椅、地面.这一周三个班的各项卫生成绩(单位:分)分别如下表:
黑板 门窗 桌椅 地面
(1)班 95 90 95 95
(2)班 90 92 85 90
(3)班 85 90 90 90
总评时将黑板、门窗、桌椅、地面这四项得分按15%,10%,35%,40%的比例计算各班的卫生成绩,哪个班的成绩最高?
19.为提高中学生网络安全意识,我县某中学特举办“网络安全知识答题竞赛”,八年级(1)、(2)班根据初赛成绩各选出5名选手代表各班参加学校决赛,两个班各选出的5名选手的决赛成绩(单位:分)如下:
八年级(1)班:75 80 85 85 100
八年级(2)班:70 100 100 75 80
分析数据如下表所示:
平均数(分) 中位数(分) 众数(分) 方差(分2)
八年级(1)班 a 85 b 70
八年级(2)班 85 c 100 160
(1)上表中的a,b,c分别是多少?
(2)分析两个班的平均数和方差,你认为哪个班的决赛成绩较好?为什么?
20.近年来网约车给人们的出行带来了便利,小明和数学兴趣小组的同学对甲、乙两家约车公司司机月收入进行了抽样调查,两家公司分别抽取的10名司机月收入(单位:千元)如图所示:
根据以上信息,整理分析数据如下:
平均月收入/千元 中位数 众数 方差
甲公司 a 6 c d
乙公司 6 b 4 7.6
(1)填空:a= ;b= ;c= ;d= .
(2)小明的叔叔计划从两家公司中选择一家做网约车司机,如果你是小明,你建议他选哪家公司?请说明理由.
21.某校八年级(1)班的学生利用春节寒假期间参加社会实践活动,到“山东惠民鑫诚农业科技园”了解大棚热带水果的生长情况.他们分两组对柠檬树的长势进行观察测量,分别收集到10株柠檬树的高度,记录如下(单位:厘米):
第一组:132,139,145,155,160,154,160,128,156,141;
第二组:151,156,144,146,140,153,137,147,150,146.
根据以上数据,回答下列问题:
(1)第一组这10株柠檬树高度的平均数是 ;中位数是 ,众数是 ;
(2)小明同学计算出第一组的方差为s12=122.2,请你计算第二组的方差,并说明哪一组柠檬树长势比较整齐.
参考答案
一.选择题
1.解:∵S=3.2,S=5.2,S=7.3,S=3.1,
∴S<S<S<S,
∴这四个城市年降水量最稳定的是丁,
故选:D.
2.解:A.甲队数据重新排列为7、7、8、9、9、9、10、10、10、10,所以甲队数据的中位数是=9(分),此选项错误;
B.乙队成绩的众数是10分,此选项正确;
C.∵==8.9,==9.1,
∴=×[2×(7﹣8.9)2+(8﹣8.9)2+3×(9﹣8.9)2+4×(10﹣8.9)2]=1.29,
=×[(7﹣9.1)2+2×(8﹣9.1)2+2×(9﹣9.1)2+5×(10﹣9.1)2]=1.09,
∴<,
∴乙队的成绩比较稳定,此选项错误;
D.由C选项知乙队的平均成绩是9.1分,此选项错误;
故选:B.
3.解:∵一个样本的每一个数据都减少3,样本数据的波动幅度不会发生变化,
∴统计量不变的是方差,
故选:D.
4.解:这组数据的中位数是第25、26个数据的平均数,由条形统计图知第25、26个数据分别为10、10,
所以这组数据的中位数为=10(元),
这组数据中出现次数最多的是10元,有20次,
所以这组数据的众数为10元,
故选:C.
5.解:∵乙和丁的平均数最小,
∴从甲和丙中选择一人参加比赛,
∵丙的方差最小,
∴选择丙参赛.
故选:C.
6.解:小明考核的最后得分为=84(分),
故选:B.
7.解:原数据重新排列为86,88,90,92,94,100,
新数据重新排列为43,44,45,46,47,50,
所以新数据是将原数据分别乘所得,
∵原数据的方差为S02,
∴新数据的方差为()2×S02=S02,
故选:C.
8.解:这组数据中出现次数最多的是14,出现5次,
所以这组数据的众数是14,故A选项错误;
中位数是=14(个),故B选项错误;
平均数为=14(个),故C选项正确;
方差为×[3×(13﹣14)2+5×(14﹣14)2+(15﹣14)2+(16﹣14)2]=0.8,故D选项错误;
故选:C.
二.填空题
9.解:因为数据4,3,6,x的平均数是4,
所以=4,
解得:x=3,
方差为:×[(4 4)2+(3 4)2+(6 4)2+(3 4)2]=,
故答案为:.
10.解:设五个数从小到大为a1,a2,a3,a4,a5,
依题意得a3=4,a4=a5=6,
a1,a2是1,2,3中两个不同的数,
符合题意的五个数可能有三种情形:
“1,2,4,6,6”,“1,3,4,6,6”,“2,3,4,6,6”,
1+2+4+6+6=19,1+3+4+6+6=20,2+3+4+6+6=21,
则这5个数的和最大值是21.
故答案为21.
11.解:∵数据x1,x2,x3,方差是2,
∴数据2x1﹣4,2x2﹣4,2x3﹣4的方差22×2=8.
故答案为:8.
12.解:∵每千克x元的糖果a千克,每千克y元的糖果b千克,
∴混合后共有(a+b)千克,混合糖果共售(ax+by)元,
∴混合糖果的售价定为每千克元.
故答案为:.
13.解:设小明同学完成数学作业的时间是x分钟,
根据题意,得:=21,
解得x=21,
∴小明同学完成数学作业的时间是21分钟,
故答案为:21.
14.解:从小到大排列的五个数x,3,6,8,12的中位数是6,
∵再加入一个数,这六个数的中位数与原来五个数的中位数相等,
∴加入的一个数是6,
∵这六个数的平均数与原来五个数的平均数相等,
∴(x+3+6+8+12)=(x+3+6+6+8+12),
解得x=1.
所以加入的数为6,x=1.
故答案为:6,1.
15.解:这个小组学生的平均得分==89(分),
故答案为:89分.
16.解:∵1,2,3,4,5的方差为2,
∴2021,2022,2023,2024,2025的方差为2,
故答案为:2.
三.解答题
17.解:(1)甲组的平均成绩为×(7×1+8×9+9×5+10×5)=8.7,
由题意可得:1+9+5+5+2+9+6+m=40,解得m=3,
甲组成绩一共有20个,从小到大最中间为8和9,则中位数为=8.5,
乙组成绩中最多的为8,则众数为8,
故答案为:8.7、3、8.5、8;
(2)==8.5,
==0.75,
∵<,
∴乙组的成绩更加稳定.
18.解:(1)班的加权平均成绩是:95×15%+90×10%+95×35%+95×40%=94.5(分),
(2)班的加权平均成绩是:90×15%+92×10%+85×35%+90×40%=88.45(分),
(3)班的加权平均成绩是:85×15%+90×10%+90×35%+90×40%=89.25(分),
∵94.5>89.25>88.45,
∴(1)班的成绩高.
19.解:(1)八年级(1)班成绩的平均数a==85,众数b=85;
将八年级(2)班成绩重新排列为70、75、80、100、100,
∴八年级(1)班成绩的中位数c=80;
(2)八年级(1)班的成绩好.
因为两个班的平均分都是85分,不分上下,而八年级(1)班的方差70小于八年级(2)班的方差160,方差越小越稳定.
所以八年级(1)班的成绩好.
20.解:(1)∵“6千元”对应的百分比为1﹣(10%+20%+10%+20%)=40%,
∴甲公司平均月收入a=4×10%+5×20%+6×40%+7×20%+8×10%=6,
众数c=6,
方差d=[(4﹣6)2+2×(5﹣6)2+4×(6﹣6)2+2×(7﹣6)2+(8﹣6)2]=1.2;
乙公司中位数b==4.5,
故答案为:6;4.5;6;1.2;
(2)选甲公司,理由如下:
因为平均数相同,中位数、众数甲公司均大于乙公司,且甲公司方差小,更稳定,所以选甲公司.
解:(1)第一组这10株柠檬树高度的平均数是
(132+139+145+155+160+154+160+128+156+141)÷10=147(厘米).
把这些数据从小到大排列为128、132、139、141、145、154、155、156、160、160,
最中间的两个数是145和154,则中位数是(145+154)÷2=149.5(厘米).
160出现了2次,出现的次数最多,则众数是160厘米.
故答案为:147厘米,149.5厘米,160厘米;
∵第二组这10株柠檬树高度的平均数是
(151+156+144+146+140+153+137+147+150+146)÷10=147,
∴S22=×[(151﹣147)2+(156﹣147)2+(144﹣147)2+(146﹣147)2+(140﹣147)2+(153﹣147)2+(137﹣147)2+(147﹣147)2+(150﹣147)2+(146﹣147)2]=30.2,
∵S12=122.2>S22,
∴第二组柠檬树长势比较整齐.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
