浙教版七年级数学下册第3章整式的乘除单元达标测试题(word解析版)
文档属性
| 名称 | 浙教版七年级数学下册第3章整式的乘除单元达标测试题(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 51.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-15 13:17:08 | ||
图片预览



文档简介
2021-2022学年浙教版七年级数学下册《第3章整式的乘除》单元达标测试题(附答案)
一、选择题(本题共计10小题,每题3分,共计30分,)
1.下列计算正确的是( )
A.(2a﹣1)2=4a2﹣1 B.3a6÷3a3=a2
C.(﹣ab2)4=﹣a4b6 D.﹣2a+(2a﹣1)=﹣1
2.若m、n、p是正整数,则(xm xn)p=( )
A.xm xnp B.xmnp C.xmp+np D.xmp np
3.下列各式运算正确的是( )
A.5a2﹣3a2=2 B.a2 a3=a6
C.(a10)2=a20 D.x(a﹣b+1)=ax﹣bx
4.若5x=a,5y=b,则52x﹣y=( )
A. B.a2b C. D.2ab
5.计算(ab2)3的结果,正确的是( )
A.a3b6 B.a3b5 C.ab6 D.ab5
6.下列四个算式:①63+63;②(2×63)×(3×63);③(22×32)3;④(33)2×(22)3中,结果等于66的是( )
A.①②③ B.②③④ C.②③ D.③④
7.若x2+2mx+16是完全平方式,则(m﹣1)2+2的值是( )
A.11 B.3 C.11或27 D.3或11
8.若2a=3,2b=5,2c=15,则( )
A.a+b=c B.a+b+1=c C.2a+b=c D.2a+2b=c
9.若x+m与x+乘积的值不含x项,则m的值为( )
A. B.4 C.﹣ D.﹣4
10.下列计算中,正确的是( )
A.(﹣2a﹣5)(2a﹣5)=25﹣4a2 B.(a﹣b)2=a2﹣b2
C.(x+3)(x﹣2)=x2﹣6 D.﹣a(2a2﹣1)=﹣2a3﹣a
二、填空题(本题共计7小题,每题3分,共计21分,)
11.已知2a2+2b2=10,a+b=3,则ab= .
12.已知x+y=﹣4,x﹣y=2,则x2﹣y2= .
13.已知 (x﹣a)(x+a)=x2﹣9,那么a= .
14.若n为正整数,且x2n=5,则(3x3n)2﹣45(x2)2n的值为 .
15.已知x﹣y=5,xy=3,则(x+y)2= .
16.有9张边长为a的正方形纸片,9张边长分别为a,b(a<b)的长方形纸片,10张边长为b的正方形纸片,从其中取出若干张纸片,每种纸片至少取一张,把取出的这些纸片拼成一个正方形(按原纸张进行无空隙、无重叠拼接),则拼成的正方形的边长最长为 .
17.如图,在边长为a的正方形中剪去一个边长为b的小正方形(a>b),把剩下的部分拼成一个梯形,分别计算这两个图形阴影部分的面积,验证了公式 .
三、解答题(本题共计8小题,共计69分,)
18.若(x﹣2)x+1=1,求x的值.
19.若5x﹣3y+2=0,求(102x)3÷(10x 103y)的值.
20.计算:(3x3y2z﹣1)﹣2 (5xy﹣2z3)2.
21.计算
(1)(﹣a2b3)3 (﹣2a2b)3;
(2)(a2)5+(﹣a2 a3)2+(﹣a2)5﹣a a9;
(3)2(x+1)+x(x+2)﹣(x﹣1)(x+5)
22.先化简,再求值:[(x﹣2y)2+(x﹣2y)(x+2y)﹣2x(2x﹣y)]÷2x,其中x=﹣1,y=﹣2023.
23.计算(×××…××1)10 (10×9×8×7×…×3×2×1)10.
24.乘法公式的探究及应用.
(1)如图1,是将图2阴影部分裁剪下来,重新拼成的一个长方形,面积是
;如图2,阴影部分的面积是 ;比较图1,图2阴影部分的面积,可以得到乘法公式 ;
(2)运用你所得到的公式,计算下列各题:
①103×97; ②(2x+y﹣3)(2x﹣y+3).
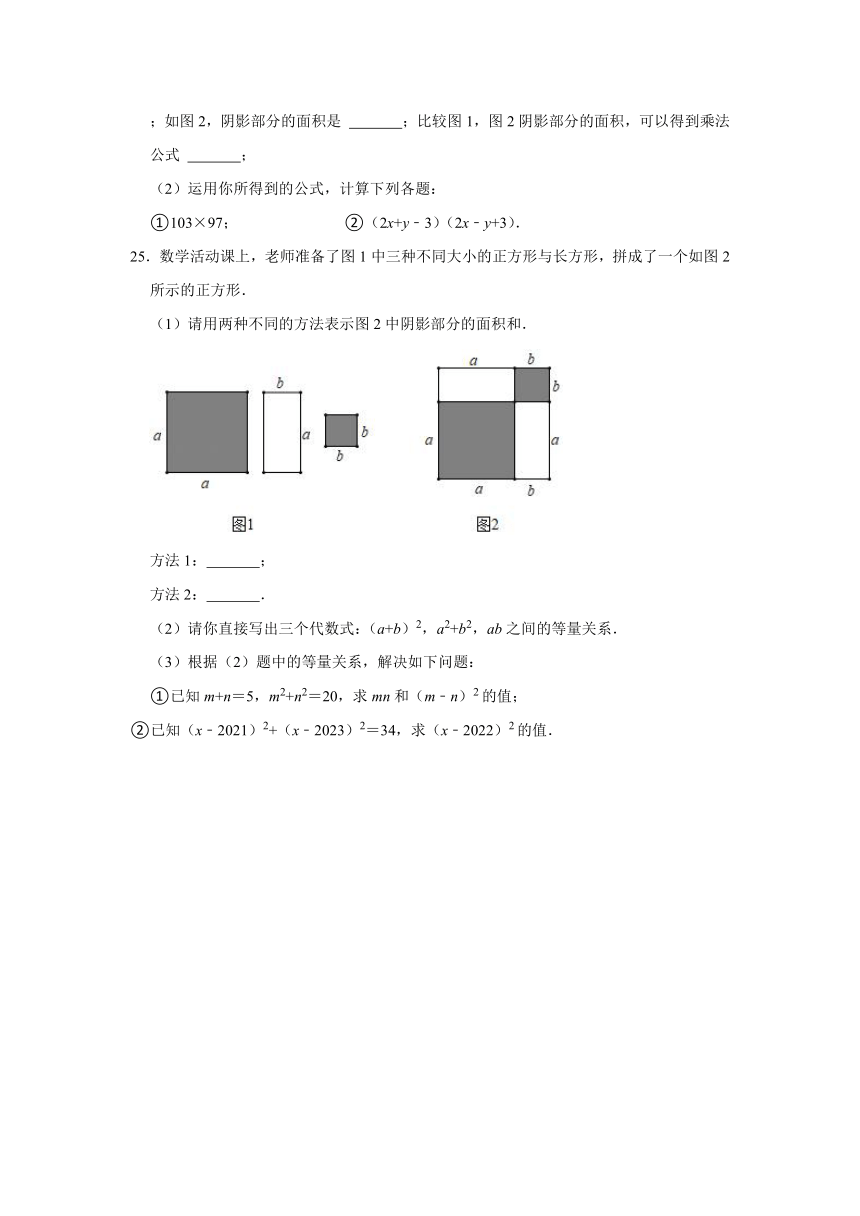
25.数学活动课上,老师准备了图1中三种不同大小的正方形与长方形,拼成了一个如图2所示的正方形.
(1)请用两种不同的方法表示图2中阴影部分的面积和.
方法1: ;
方法2: .
(2)请你直接写出三个代数式:(a+b)2,a2+b2,ab之间的等量关系.
(3)根据(2)题中的等量关系,解决如下问题:
①已知m+n=5,m2+n2=20,求mn和(m﹣n)2的值;
②已知(x﹣2021)2+(x﹣2023)2=34,求(x﹣2022)2的值.
参考答案
一、选择题(本题共计10小题,每题3分,共计30分,)
1.解:A、原式=4a2﹣4a+1,不符合题意;
B、原式=a3,不符合题意;
C、原式=a4b8,不符合题意;
D、原式=﹣2a+2a﹣1=﹣1,符合题意,
故选:D.
2.解:(xm xn)p
=(xm+n)p
=x(m+n)p
=xmp+np,
故选:C.
3.解:∵5a2﹣3a2=2a2≠2,故选项A错误;
a2 a3=a5≠a6,故选项B错误;
(a10)2=a20,故选项C正确;
x(a﹣b+1)=ax﹣bx+x≠ax﹣bx,故选项D错误;
故选:C.
4.解:52x﹣y=52x÷5y=5x×5x÷5y
已知5x=a,5y=b,所以上式=.
故选:A.
5.解:(ab2)3=a3b6.
故选:A.
6.解:①63+63=2×63;
②(2×63)×(3×63)=6×66=67;
③(22×32)3=(62)3=66;
④(33)2×(22)3=36×26=66.
所以③④两项的结果是66.
故选:D.
7.解:∵x2+2mx+16是完全平方式.
∴m2=16.
∴m=±4.
当m=4时,(m﹣1)2+2=9+2=11.
当m=﹣4时(m﹣1)2+2=25+2=27.
故答案为:C.
故选:C.
8.解:∵2a×2b=2a+b=3×5=15=2c,
∴a+b=c,
故选:A.
9.解:(x+m)(x+)=x2+(m+)x+m,
∵乘积中不含x项,
∴m+=0,即m=﹣.
故选:C.
10.解:A、(﹣2a﹣5)(2a﹣5)=25﹣4a2,正确;
B、(a﹣b)2=a2﹣2ab+b2,错误;
C、(x+3)(x﹣2)=x2+x﹣6,错误;
D、﹣a(2a2﹣1)=﹣2a3+a,错误,
故选:A.
二、填空题(本题共计7小题,每题3分,共计21分,)
11.解:∵2a2+2b2=10,
∴a2+b2=5,
∵a+b=3,
∴(a+b)2=9,
∴a2+2ab+b2=9,
∴5+2ab=9,
∴2ab=4,
∴ab=2,
故答案为:2.
12.解:当x+y=﹣4,x﹣y=2时,
原式=(x+y)(x﹣y)
=﹣4×2
=﹣8.
故答案为:﹣8.
13.解:根据平方差公式,
(x﹣a)(x+a)=x2﹣a2,
由已知可得,a2=9,
所以,a=±=±3.
故答案为:±3.
14.解:当x2n=5时,
原式=9x6n﹣45x4n
=9(x2n)3﹣45(x2n)2
=9×53﹣45×52
=9×53﹣9×53
=0.
故答案为:0.
15.解:将x﹣y=5两边平方得:(x﹣y)2=25,
即(x+y)2=x2+y2+2xy=x2+y2﹣2xy+4xy=(x﹣y)2+4xy,
把xy=3代入得:(x+y)2=(x﹣y)2+4xy=25+4×3=37.
故答案为:37.
16.解:假设正方形的边长为xa+yb,其中x、y为正整数.
则(xa+yb)2≤9a2+9b2+10ab,
x2a2+2xyab+y2b2≤9a2+9b2+10ab,
即(9﹣x2)a2+(9﹣y2)b2+(10﹣2xy)ab≥0.
∵a<b,
∴9﹣y2≥0,y≤3.
当y取最大值3时,由10﹣2xy≥0,得x≤1,即x取最大值1.
∴拼成得正方形边长最长为:3b+a.
故答案为:3b+a.
17.解:a2﹣b2=(a+b)(a﹣b).
三、解答题(本题共计9小题,共计69分,)
18.解:①依题意得:x+1=0,且x﹣2≠0
解得x=﹣1.
②依题意得:x﹣2=1,即x=3时,也符合题意;
③依题意得:当x﹣2=﹣1即x=1时,也符合题意.
综上所述,x的值是﹣1或3或1.
19.解:5x﹣3y+2=0则5x﹣3y=﹣2.
原式=106x÷10x+3y
=106x﹣x﹣3y
=105x﹣3y
=10﹣2
=.
20.解:原式=3﹣2x﹣6y﹣4z2 25x2y﹣4z6
=(×25) x﹣6+2 y﹣4﹣4 z2+6
=.
21.解:(1)(﹣a2b3)3 (﹣2a2b)3
=﹣a6b9 (﹣8a6b3)
=a12b12;
(2)(a2)5+(﹣a2 a3)2+(﹣a2)5﹣a a9
=a10+a10﹣a10﹣a10
=0;
(3)2(x+1)+x(x+2)﹣(x﹣1)(x+5)
=2x+2+x2+2x﹣x2﹣5x+x+5
=7.
22.解:[(x﹣2y)2+(x﹣2y)(x+2y)﹣2x(2x﹣y)]÷2x
=(x2﹣4xy+4y2+x2﹣4y2﹣4x2+2xy)÷2x
=(﹣2x2﹣2xy)÷2x
=﹣x﹣y,
当x=﹣1,y=﹣2023时,原式=1+2023=2022.
23.解:(×××…××1)10 (10×9×8×7×…×3×2×1)10=(×××…××1×10×9×8×7×…×3×2×1)10=110=1;
24.解:(1)由拼图可知,图形1的长为(a+b),宽为(a﹣b),因此面积为(a+b)(a﹣b),图形2的阴影部分的面积为两个正方形的面积差,即a2﹣b2,
由图形1,图形2的面积相等可得,(a+b)(a﹣b)=a2﹣b2,
故答案为:(a+b)(a﹣b),a2﹣b2,(a+b)(a﹣b)=a2﹣b2;
(2)①103×97=(100+3)(100﹣3)
=1002﹣32
=10000﹣9
=9991;
②原式=(2x+y﹣3)
=(2x)2﹣(y﹣3)2
=4x2﹣(y2﹣6y+9)
=4x2﹣y2+6y﹣9.
25.解:(1)阴影两部分求和为a2+b2,用总面积减去空白部分面积为(a+b)2﹣2ab,
故答案为:a2+b2,(a+b)2﹣2ab;
(2)由题意得,a2+b2=(a+b)2﹣2ab;
(3)①由(2)题结论a2+b2=(a+b)2﹣2ab可得ab=,
∴m+n=5,m2+n2=20时,
mn=
=
=,
(m﹣n)2
=m2﹣2mn+n2;
=20﹣2×
=20﹣5
=15;
②设a=x﹣2021,b=x﹣2023,
可得a+b=(x﹣2021)+(x﹣2023)
=x﹣2021+x﹣2023
=2x﹣4044
=2(x﹣2022),
由(2)题结论a2+b2=(a+b)2﹣2ab可得,
(a+b)2=a2+2ab+b2,
又∵(a﹣b)2=[(x﹣2021)﹣(x﹣2023)]2=22=4,
且由(a﹣b)2=a2﹣2ab+b2,可得2ab=(a2+b2)﹣(a﹣b)2=(x﹣2021)2+(x﹣2023)2﹣[(x﹣2021)﹣(x﹣2023)]2=34﹣4=30,
∴(x﹣2022)2=()2====16.
一、选择题(本题共计10小题,每题3分,共计30分,)
1.下列计算正确的是( )
A.(2a﹣1)2=4a2﹣1 B.3a6÷3a3=a2
C.(﹣ab2)4=﹣a4b6 D.﹣2a+(2a﹣1)=﹣1
2.若m、n、p是正整数,则(xm xn)p=( )
A.xm xnp B.xmnp C.xmp+np D.xmp np
3.下列各式运算正确的是( )
A.5a2﹣3a2=2 B.a2 a3=a6
C.(a10)2=a20 D.x(a﹣b+1)=ax﹣bx
4.若5x=a,5y=b,则52x﹣y=( )
A. B.a2b C. D.2ab
5.计算(ab2)3的结果,正确的是( )
A.a3b6 B.a3b5 C.ab6 D.ab5
6.下列四个算式:①63+63;②(2×63)×(3×63);③(22×32)3;④(33)2×(22)3中,结果等于66的是( )
A.①②③ B.②③④ C.②③ D.③④
7.若x2+2mx+16是完全平方式,则(m﹣1)2+2的值是( )
A.11 B.3 C.11或27 D.3或11
8.若2a=3,2b=5,2c=15,则( )
A.a+b=c B.a+b+1=c C.2a+b=c D.2a+2b=c
9.若x+m与x+乘积的值不含x项,则m的值为( )
A. B.4 C.﹣ D.﹣4
10.下列计算中,正确的是( )
A.(﹣2a﹣5)(2a﹣5)=25﹣4a2 B.(a﹣b)2=a2﹣b2
C.(x+3)(x﹣2)=x2﹣6 D.﹣a(2a2﹣1)=﹣2a3﹣a
二、填空题(本题共计7小题,每题3分,共计21分,)
11.已知2a2+2b2=10,a+b=3,则ab= .
12.已知x+y=﹣4,x﹣y=2,则x2﹣y2= .
13.已知 (x﹣a)(x+a)=x2﹣9,那么a= .
14.若n为正整数,且x2n=5,则(3x3n)2﹣45(x2)2n的值为 .
15.已知x﹣y=5,xy=3,则(x+y)2= .
16.有9张边长为a的正方形纸片,9张边长分别为a,b(a<b)的长方形纸片,10张边长为b的正方形纸片,从其中取出若干张纸片,每种纸片至少取一张,把取出的这些纸片拼成一个正方形(按原纸张进行无空隙、无重叠拼接),则拼成的正方形的边长最长为 .
17.如图,在边长为a的正方形中剪去一个边长为b的小正方形(a>b),把剩下的部分拼成一个梯形,分别计算这两个图形阴影部分的面积,验证了公式 .
三、解答题(本题共计8小题,共计69分,)
18.若(x﹣2)x+1=1,求x的值.
19.若5x﹣3y+2=0,求(102x)3÷(10x 103y)的值.
20.计算:(3x3y2z﹣1)﹣2 (5xy﹣2z3)2.
21.计算
(1)(﹣a2b3)3 (﹣2a2b)3;
(2)(a2)5+(﹣a2 a3)2+(﹣a2)5﹣a a9;
(3)2(x+1)+x(x+2)﹣(x﹣1)(x+5)
22.先化简,再求值:[(x﹣2y)2+(x﹣2y)(x+2y)﹣2x(2x﹣y)]÷2x,其中x=﹣1,y=﹣2023.
23.计算(×××…××1)10 (10×9×8×7×…×3×2×1)10.
24.乘法公式的探究及应用.
(1)如图1,是将图2阴影部分裁剪下来,重新拼成的一个长方形,面积是
;如图2,阴影部分的面积是 ;比较图1,图2阴影部分的面积,可以得到乘法公式 ;
(2)运用你所得到的公式,计算下列各题:
①103×97; ②(2x+y﹣3)(2x﹣y+3).
25.数学活动课上,老师准备了图1中三种不同大小的正方形与长方形,拼成了一个如图2所示的正方形.
(1)请用两种不同的方法表示图2中阴影部分的面积和.
方法1: ;
方法2: .
(2)请你直接写出三个代数式:(a+b)2,a2+b2,ab之间的等量关系.
(3)根据(2)题中的等量关系,解决如下问题:
①已知m+n=5,m2+n2=20,求mn和(m﹣n)2的值;
②已知(x﹣2021)2+(x﹣2023)2=34,求(x﹣2022)2的值.
参考答案
一、选择题(本题共计10小题,每题3分,共计30分,)
1.解:A、原式=4a2﹣4a+1,不符合题意;
B、原式=a3,不符合题意;
C、原式=a4b8,不符合题意;
D、原式=﹣2a+2a﹣1=﹣1,符合题意,
故选:D.
2.解:(xm xn)p
=(xm+n)p
=x(m+n)p
=xmp+np,
故选:C.
3.解:∵5a2﹣3a2=2a2≠2,故选项A错误;
a2 a3=a5≠a6,故选项B错误;
(a10)2=a20,故选项C正确;
x(a﹣b+1)=ax﹣bx+x≠ax﹣bx,故选项D错误;
故选:C.
4.解:52x﹣y=52x÷5y=5x×5x÷5y
已知5x=a,5y=b,所以上式=.
故选:A.
5.解:(ab2)3=a3b6.
故选:A.
6.解:①63+63=2×63;
②(2×63)×(3×63)=6×66=67;
③(22×32)3=(62)3=66;
④(33)2×(22)3=36×26=66.
所以③④两项的结果是66.
故选:D.
7.解:∵x2+2mx+16是完全平方式.
∴m2=16.
∴m=±4.
当m=4时,(m﹣1)2+2=9+2=11.
当m=﹣4时(m﹣1)2+2=25+2=27.
故答案为:C.
故选:C.
8.解:∵2a×2b=2a+b=3×5=15=2c,
∴a+b=c,
故选:A.
9.解:(x+m)(x+)=x2+(m+)x+m,
∵乘积中不含x项,
∴m+=0,即m=﹣.
故选:C.
10.解:A、(﹣2a﹣5)(2a﹣5)=25﹣4a2,正确;
B、(a﹣b)2=a2﹣2ab+b2,错误;
C、(x+3)(x﹣2)=x2+x﹣6,错误;
D、﹣a(2a2﹣1)=﹣2a3+a,错误,
故选:A.
二、填空题(本题共计7小题,每题3分,共计21分,)
11.解:∵2a2+2b2=10,
∴a2+b2=5,
∵a+b=3,
∴(a+b)2=9,
∴a2+2ab+b2=9,
∴5+2ab=9,
∴2ab=4,
∴ab=2,
故答案为:2.
12.解:当x+y=﹣4,x﹣y=2时,
原式=(x+y)(x﹣y)
=﹣4×2
=﹣8.
故答案为:﹣8.
13.解:根据平方差公式,
(x﹣a)(x+a)=x2﹣a2,
由已知可得,a2=9,
所以,a=±=±3.
故答案为:±3.
14.解:当x2n=5时,
原式=9x6n﹣45x4n
=9(x2n)3﹣45(x2n)2
=9×53﹣45×52
=9×53﹣9×53
=0.
故答案为:0.
15.解:将x﹣y=5两边平方得:(x﹣y)2=25,
即(x+y)2=x2+y2+2xy=x2+y2﹣2xy+4xy=(x﹣y)2+4xy,
把xy=3代入得:(x+y)2=(x﹣y)2+4xy=25+4×3=37.
故答案为:37.
16.解:假设正方形的边长为xa+yb,其中x、y为正整数.
则(xa+yb)2≤9a2+9b2+10ab,
x2a2+2xyab+y2b2≤9a2+9b2+10ab,
即(9﹣x2)a2+(9﹣y2)b2+(10﹣2xy)ab≥0.
∵a<b,
∴9﹣y2≥0,y≤3.
当y取最大值3时,由10﹣2xy≥0,得x≤1,即x取最大值1.
∴拼成得正方形边长最长为:3b+a.
故答案为:3b+a.
17.解:a2﹣b2=(a+b)(a﹣b).
三、解答题(本题共计9小题,共计69分,)
18.解:①依题意得:x+1=0,且x﹣2≠0
解得x=﹣1.
②依题意得:x﹣2=1,即x=3时,也符合题意;
③依题意得:当x﹣2=﹣1即x=1时,也符合题意.
综上所述,x的值是﹣1或3或1.
19.解:5x﹣3y+2=0则5x﹣3y=﹣2.
原式=106x÷10x+3y
=106x﹣x﹣3y
=105x﹣3y
=10﹣2
=.
20.解:原式=3﹣2x﹣6y﹣4z2 25x2y﹣4z6
=(×25) x﹣6+2 y﹣4﹣4 z2+6
=.
21.解:(1)(﹣a2b3)3 (﹣2a2b)3
=﹣a6b9 (﹣8a6b3)
=a12b12;
(2)(a2)5+(﹣a2 a3)2+(﹣a2)5﹣a a9
=a10+a10﹣a10﹣a10
=0;
(3)2(x+1)+x(x+2)﹣(x﹣1)(x+5)
=2x+2+x2+2x﹣x2﹣5x+x+5
=7.
22.解:[(x﹣2y)2+(x﹣2y)(x+2y)﹣2x(2x﹣y)]÷2x
=(x2﹣4xy+4y2+x2﹣4y2﹣4x2+2xy)÷2x
=(﹣2x2﹣2xy)÷2x
=﹣x﹣y,
当x=﹣1,y=﹣2023时,原式=1+2023=2022.
23.解:(×××…××1)10 (10×9×8×7×…×3×2×1)10=(×××…××1×10×9×8×7×…×3×2×1)10=110=1;
24.解:(1)由拼图可知,图形1的长为(a+b),宽为(a﹣b),因此面积为(a+b)(a﹣b),图形2的阴影部分的面积为两个正方形的面积差,即a2﹣b2,
由图形1,图形2的面积相等可得,(a+b)(a﹣b)=a2﹣b2,
故答案为:(a+b)(a﹣b),a2﹣b2,(a+b)(a﹣b)=a2﹣b2;
(2)①103×97=(100+3)(100﹣3)
=1002﹣32
=10000﹣9
=9991;
②原式=(2x+y﹣3)
=(2x)2﹣(y﹣3)2
=4x2﹣(y2﹣6y+9)
=4x2﹣y2+6y﹣9.
25.解:(1)阴影两部分求和为a2+b2,用总面积减去空白部分面积为(a+b)2﹣2ab,
故答案为:a2+b2,(a+b)2﹣2ab;
(2)由题意得,a2+b2=(a+b)2﹣2ab;
(3)①由(2)题结论a2+b2=(a+b)2﹣2ab可得ab=,
∴m+n=5,m2+n2=20时,
mn=
=
=,
(m﹣n)2
=m2﹣2mn+n2;
=20﹣2×
=20﹣5
=15;
②设a=x﹣2021,b=x﹣2023,
可得a+b=(x﹣2021)+(x﹣2023)
=x﹣2021+x﹣2023
=2x﹣4044
=2(x﹣2022),
由(2)题结论a2+b2=(a+b)2﹣2ab可得,
(a+b)2=a2+2ab+b2,
又∵(a﹣b)2=[(x﹣2021)﹣(x﹣2023)]2=22=4,
且由(a﹣b)2=a2﹣2ab+b2,可得2ab=(a2+b2)﹣(a﹣b)2=(x﹣2021)2+(x﹣2023)2﹣[(x﹣2021)﹣(x﹣2023)]2=34﹣4=30,
∴(x﹣2022)2=()2====16.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
