2021-2022学年浙教版七年级数学下册2.4二元一次方程组的应用同步练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年浙教版七年级数学下册2.4二元一次方程组的应用同步练习题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 106.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 13:12:18 | ||
图片预览



文档简介
2021-2022学年浙教版七年级数学下册《2-4二元一次方程组的应用》同步练习题(附答案)
一.选择题
1.某人带了100元去市场买水果,他买了1千克的哈密瓜,2千克的青提葡萄,还剩30元.设哈密瓜每千克x元,青提葡萄每千克y元,得方程x+2y=70.则下列说法中,正确的是( )
A.1千克青提葡萄的价格可以是36元
B.若1千克哈密瓜的价格是12元,则1千克青提葡萄的价格是20元
C.若是方程x+2y=70的解,则m,n都可以表示哈密瓜、青提葡萄的单价
D.若m,n分别表示哈密瓜、青提葡萄的单价,则m,n一定是方程x+2y=70的解
2.某次知识竞赛共有20道题,规定:每答对一题得+5分,每答错一题得﹣3分,不答的题得﹣1分.已知欢欢这次竞赛得了72分,设欢欢答对了x道题,答错了y道题,则( )
A.5x﹣3y=72 B.5x+3y=72 C.6x﹣2y=92 D.6x+2y=92
3.一辆轿车行驶2小时的路程比一辆卡车行驶3小时的路程少40千米.如果设轿车平均速度为a千米/小时,卡车的平均速度为b千米/小时,则( )
A.2a=3b+40 B.3b=2a﹣40 C.2a=3b﹣40 D.3b=40﹣2a
4.玩具车间每天能生产甲种玩具零件24个或乙种玩具零件12个,若甲种玩具零件一个与乙种玩具零件2个能组成一个完整的玩具,怎样安排生产才能在60天内组装出最多的玩具设生产甲种玩具零件x天,乙种玩具零件y天,则有( )
A. B.
C. D.
5.我国古代数学名著《张邱建算经》中记载:“今有清酒一斗直粟十斗,醑酒一斗直粟三斗.今持粟三斛,得酒五斗,问清、醑酒各几何?意思是:现在一斗清酒价值10斗谷子,一斗醑酒价值3斗谷子,现在拿30斗谷子,共换了5斗酒,问清、醑酒各几斗?如果设清酒x斗,醑酒y斗,那么可列方程组为( )
A. B.
C. D.
二.填空题
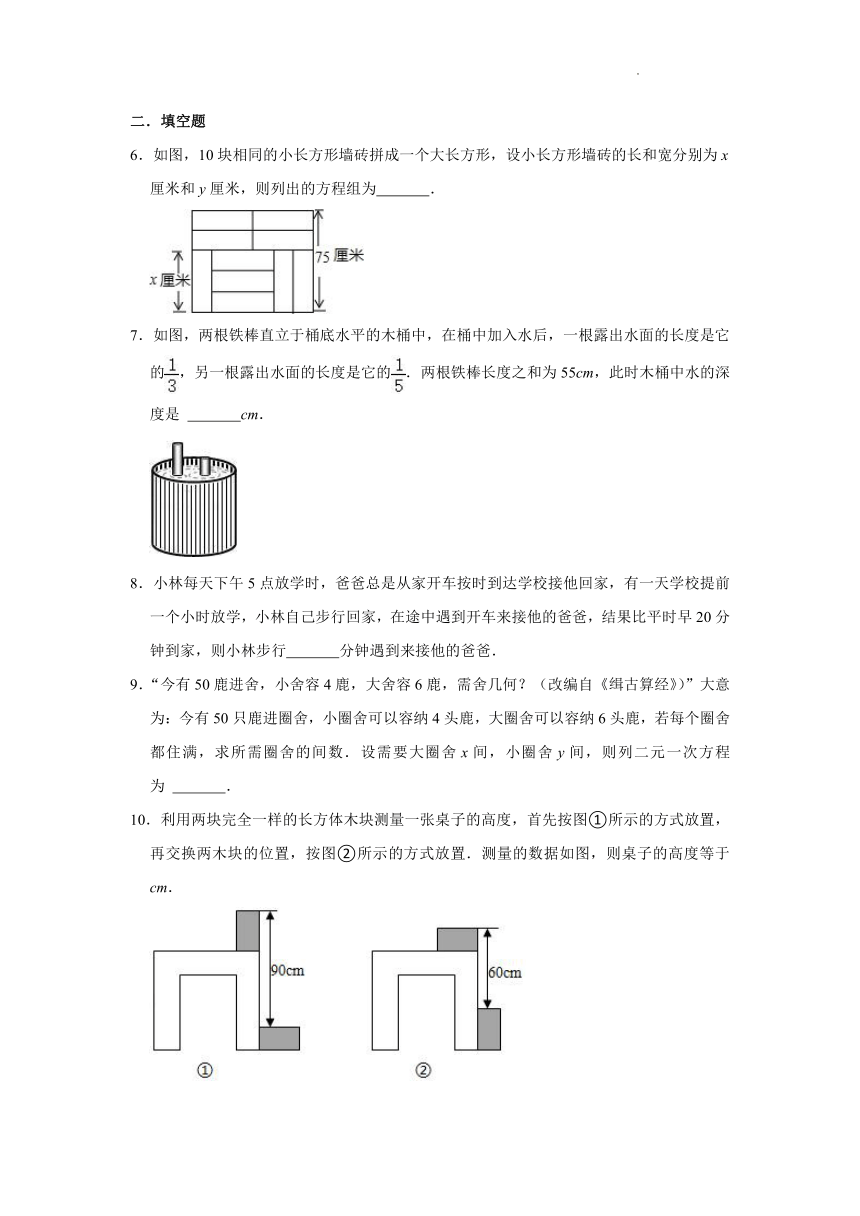
6.如图,10块相同的小长方形墙砖拼成一个大长方形,设小长方形墙砖的长和宽分别为x厘米和y厘米,则列出的方程组为 .
7.如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的,另一根露出水面的长度是它的.两根铁棒长度之和为55cm,此时木桶中水的深度是 cm.
8.小林每天下午5点放学时,爸爸总是从家开车按时到达学校接他回家,有一天学校提前一个小时放学,小林自己步行回家,在途中遇到开车来接他的爸爸,结果比平时早20分钟到家,则小林步行 分钟遇到来接他的爸爸.
9.“今有50鹿进舍,小舍容4鹿,大舍容6鹿,需舍几何?(改编自《缉古算经》)”大意为:今有50只鹿进圈舍,小圈舍可以容纳4头鹿,大圈舍可以容纳6头鹿,若每个圈舍都住满,求所需圈舍的间数.设需要大圈舍x间,小圈舍y间,则列二元一次方程为 .
10.利用两块完全一样的长方体木块测量一张桌子的高度,首先按图①所示的方式放置,再交换两木块的位置,按图②所示的方式放置.测量的数据如图,则桌子的高度等于 cm.
11.如图所示是由截面为同一种矩形的墙砖粘贴的部分墙面,其中三块横放的墙砖比两块竖放的墙砖低30cm,两块竖放的墙砖比两块横放的墙砖高50cm,则每块墙砖的截面面积是 cm2.
12.A、B两个码头相距140千米,一艘轮船在其间航行,顺流用了7小时,逆流用了10小时,则这艘轮船在静水中的速度是每小时 千米.
13.某市在落实国家“精准扶贫”政策的过程中,为某村修建一条长为400米的公路,由甲、乙两个工程队负责施工.甲工程队独立施工两天后,乙工程队加入,两工程队联合施工3天后,还剩50米的工程.已知甲工程队每天比乙工程队多施工2米,求甲、乙工程队每天各施工多少米.设甲工程队每天施工x米,乙工程队每天施工y米,根据题意,列出方程组 .
14.我国古代问题:以绳测井,若将绳三折测之,绳多四尺,若将绳四折测之,绳多一尺,井深几何?这段话的意思是:用绳子量井深,把绳三折来量,井外余绳四尺,把绳四折来量,井外余绳一尺,井深几尺?则该问题的井深是 尺.
三.解答题
15.列方程组解应用题:
甲乙两人从相距36千米的两地相向而行.如果甲比乙先走2小时,那么在乙出发后3小时相遇;如果乙比甲先走2小时,那么在甲出发后2.5小时相遇.甲、乙两人每小时各走多少千米?
16.某旅行社组织一批游客外出旅游,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满.已知45座客车租金为每辆220元,60座客车租金为每辆300元,问:
(1)这批游客的人数是多少?原计划租用多少辆45座客车?
(2)若租用同一种车,要使每位游客都有座位,应该怎样租用才合算?
17.某商场新进一种服装,每套服装售价100元,若将裤子降价10%,上衣涨价5%,调价后这套服装的单价和比原来提高了2%,这套服装原来裤子和上衣的单价分别是多少?
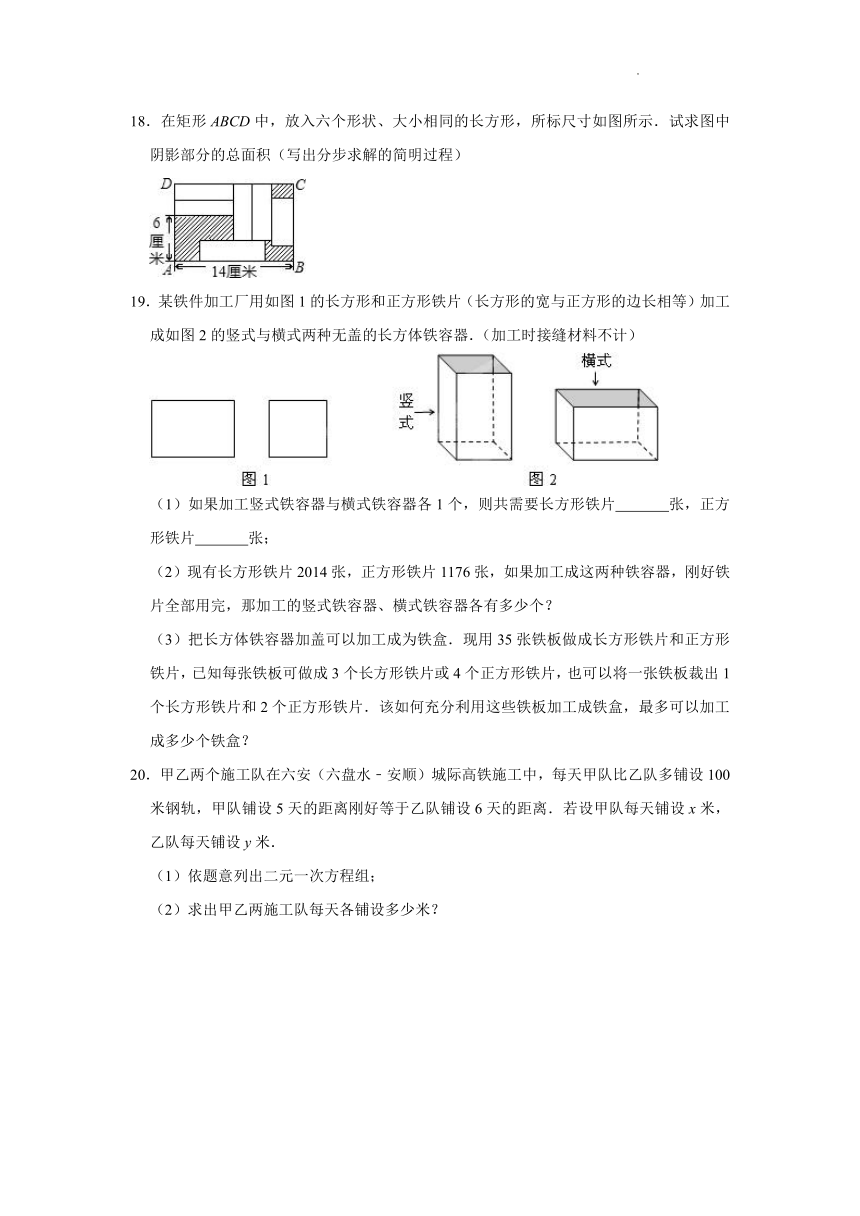
18.在矩形ABCD中,放入六个形状、大小相同的长方形,所标尺寸如图所示.试求图中阴影部分的总面积(写出分步求解的简明过程)
19.某铁件加工厂用如图1的长方形和正方形铁片(长方形的宽与正方形的边长相等)加工成如图2的竖式与横式两种无盖的长方体铁容器.(加工时接缝材料不计)
(1)如果加工竖式铁容器与横式铁容器各1个,则共需要长方形铁片 张,正方形铁片 张;
(2)现有长方形铁片2014张,正方形铁片1176张,如果加工成这两种铁容器,刚好铁片全部用完,那加工的竖式铁容器、横式铁容器各有多少个?
(3)把长方体铁容器加盖可以加工成为铁盒.现用35张铁板做成长方形铁片和正方形铁片,已知每张铁板可做成3个长方形铁片或4个正方形铁片,也可以将一张铁板裁出1个长方形铁片和2个正方形铁片.该如何充分利用这些铁板加工成铁盒,最多可以加工成多少个铁盒?
20.甲乙两个施工队在六安(六盘水﹣安顺)城际高铁施工中,每天甲队比乙队多铺设100米钢轨,甲队铺设5天的距离刚好等于乙队铺设6天的距离.若设甲队每天铺设x米,乙队每天铺设y米.
(1)依题意列出二元一次方程组;
(2)求出甲乙两施工队每天各铺设多少米?
参考答案
一.选择题
1.解:∵设哈密瓜每千克x元,青提葡萄每千克y元,得方程x+2y=70,
∴当y=36时,x=﹣2,此种情况不合实际,故选选项A不正确;
当x=12时,12+2y=70,解得y=29,故选项B不正确;
若是方程x+2y=70的解,则m,n不一定可以表示哈密瓜、青提葡萄的单价,如m=﹣2,n=36,故选项C不正确;
若m,n分别表示哈密瓜、青提葡萄的单价,则m,n一定是方程x+2y=70的解,故选项D正确;
故选:D.
2.解:设欢欢答对了x道题,答错了y道题,则:
5x﹣3y﹣(20﹣x﹣y)=72,
整理得:6x﹣2y=92.
故选:C.
3.解:根据题意得:
轿车行驶2小时的路程为:2a,
卡车行驶3小时的路程为:3b,
∵轿车行驶2小时的路程比卡车行驶3小时的路程少40千米,
∴3b﹣2a=40,
整理得:3b=2a+40,2a=3b﹣40,
故选:C.
4.解:根据总天数是60天,可得x+y=60;根据乙种零件应是甲种零件的2倍,可列方程为2×24x=12y.
则可列方程组为.
故选:C.
5.解:设清酒x斗,醑酒y斗,
依题意得:.
故选:A.
二.填空题
6.解:根据图示可得,
故答案是:.
7.解:设较长铁棒的长度为xcm,较短铁棒的长度为ycm.
因为两根铁棒之和为55cm,故可列x+y=55,
又知两棒未露出水面的长度相等,故可知x=y,
据此可列:,
解得:,
因此木桶中水的深度为30×=20cm.
故填20.
8.解:设小林自己走的路程为S.
根据题意得:=+40=+40=50(分钟).
故填50.
9.解:由题意可得,
6x+4y=50,
故答案为:6x+4y=50.
10.解:设桌子的高度为xcm,长方体木块一个面(图中展示的面)的长比宽大ycm,
依题意得:,
解得:.
故答案为:75.
11.解:设每块墙砖的长为xcm,宽为ycm,
依题意得:,
解得:,
∴xy=45×20=900(cm2).
故答案为:900.
12.解:设这艘船在静水中的速度和水流速度分别为x千米/小时,y千米/小时,
依题意得,
解得:,
答:这艘船在静水中的速度为17千米/小时,
故答案为:17.
13.解:由题意可得,
,
故答案是:.
14.解:设绳长是x尺,井深是y尺,依题意有
,
解得,.
故井深是8尺.
故答案为:8.
三.解答题
15.解:设甲,乙速度分别为x,y千米/时,
,
解得:,
甲的速度是3.6千米每小时,乙的速度是6千米每小时.
16.解:(1)设这批游客的人数是x人,原计划租用45座客车y辆.
根据题意,得,
解这个方程组,得.
答:这批游客的人数240人,原计划租45座客车5辆;
(2)租45座客车:240÷45≈5.3(辆),所以需租6辆,租金为220×6=1320(元),
租60座客车:240÷60=4(辆),所以需租4辆,租金为300×4=1200(元).
答:租用4辆60座客车更合算.
17.解:设裤子单价是x元,上衣原来的单价是y元,
依题意得:,
解得:.
答:这套服装原来裤子的单价为20元,上衣的单价是80元.
18.解:设小长方形的长为x,宽为y,如图可知,
x+3y=14,①
x+y﹣2y=6,即x﹣y=6,②
①﹣②得4y=8,y=2,代入②得x=8,
因此,大矩形ABCD的宽AD=6+2y=6+2×2=10.
矩形ABCD面积=14×10=140(平方厘米),
阴影部分总面积=140﹣6×2×8=44(平方厘米).
19.解:(1)如果加工竖式铁容器与横式铁容器各1个,则共需要长方形铁片7张,正方形铁片3张;
(2)设加工的竖式铁容器有x个,横式铁容器有y个,根据题意得,
解得
答:竖式铁容器加工100个,横式铁容器加工538个;
(3)设做长方形铁片的铁板为m块,做正方形铁片的铁板为n块,
依题意,得:,
解得:.
∵在这35块铁板中,25块做长方形铁片可做25×3=75(张),9块做正方形铁片可做9×4=36(张),剩下1块可裁出1张长方形铁片和2张正方形铁片,
∴共做长方形铁片75+1=76(张),正方形铁片36+2=38(张),
∴可做铁盒76÷4=19(个).
答:最多可以加工成19个铁盒.
20.解:(1)∵甲队每天铺设x米,乙队每天铺设y米,每天甲队比乙队多铺设100米钢轨,甲队铺设5天的距离刚好等于乙队铺设6天的距离,
∴.
(2),
解得:.
答:甲队每天铺设600米,乙队每天铺设500米.
一.选择题
1.某人带了100元去市场买水果,他买了1千克的哈密瓜,2千克的青提葡萄,还剩30元.设哈密瓜每千克x元,青提葡萄每千克y元,得方程x+2y=70.则下列说法中,正确的是( )
A.1千克青提葡萄的价格可以是36元
B.若1千克哈密瓜的价格是12元,则1千克青提葡萄的价格是20元
C.若是方程x+2y=70的解,则m,n都可以表示哈密瓜、青提葡萄的单价
D.若m,n分别表示哈密瓜、青提葡萄的单价,则m,n一定是方程x+2y=70的解
2.某次知识竞赛共有20道题,规定:每答对一题得+5分,每答错一题得﹣3分,不答的题得﹣1分.已知欢欢这次竞赛得了72分,设欢欢答对了x道题,答错了y道题,则( )
A.5x﹣3y=72 B.5x+3y=72 C.6x﹣2y=92 D.6x+2y=92
3.一辆轿车行驶2小时的路程比一辆卡车行驶3小时的路程少40千米.如果设轿车平均速度为a千米/小时,卡车的平均速度为b千米/小时,则( )
A.2a=3b+40 B.3b=2a﹣40 C.2a=3b﹣40 D.3b=40﹣2a
4.玩具车间每天能生产甲种玩具零件24个或乙种玩具零件12个,若甲种玩具零件一个与乙种玩具零件2个能组成一个完整的玩具,怎样安排生产才能在60天内组装出最多的玩具设生产甲种玩具零件x天,乙种玩具零件y天,则有( )
A. B.
C. D.
5.我国古代数学名著《张邱建算经》中记载:“今有清酒一斗直粟十斗,醑酒一斗直粟三斗.今持粟三斛,得酒五斗,问清、醑酒各几何?意思是:现在一斗清酒价值10斗谷子,一斗醑酒价值3斗谷子,现在拿30斗谷子,共换了5斗酒,问清、醑酒各几斗?如果设清酒x斗,醑酒y斗,那么可列方程组为( )
A. B.
C. D.
二.填空题
6.如图,10块相同的小长方形墙砖拼成一个大长方形,设小长方形墙砖的长和宽分别为x厘米和y厘米,则列出的方程组为 .
7.如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的,另一根露出水面的长度是它的.两根铁棒长度之和为55cm,此时木桶中水的深度是 cm.
8.小林每天下午5点放学时,爸爸总是从家开车按时到达学校接他回家,有一天学校提前一个小时放学,小林自己步行回家,在途中遇到开车来接他的爸爸,结果比平时早20分钟到家,则小林步行 分钟遇到来接他的爸爸.
9.“今有50鹿进舍,小舍容4鹿,大舍容6鹿,需舍几何?(改编自《缉古算经》)”大意为:今有50只鹿进圈舍,小圈舍可以容纳4头鹿,大圈舍可以容纳6头鹿,若每个圈舍都住满,求所需圈舍的间数.设需要大圈舍x间,小圈舍y间,则列二元一次方程为 .
10.利用两块完全一样的长方体木块测量一张桌子的高度,首先按图①所示的方式放置,再交换两木块的位置,按图②所示的方式放置.测量的数据如图,则桌子的高度等于 cm.
11.如图所示是由截面为同一种矩形的墙砖粘贴的部分墙面,其中三块横放的墙砖比两块竖放的墙砖低30cm,两块竖放的墙砖比两块横放的墙砖高50cm,则每块墙砖的截面面积是 cm2.
12.A、B两个码头相距140千米,一艘轮船在其间航行,顺流用了7小时,逆流用了10小时,则这艘轮船在静水中的速度是每小时 千米.
13.某市在落实国家“精准扶贫”政策的过程中,为某村修建一条长为400米的公路,由甲、乙两个工程队负责施工.甲工程队独立施工两天后,乙工程队加入,两工程队联合施工3天后,还剩50米的工程.已知甲工程队每天比乙工程队多施工2米,求甲、乙工程队每天各施工多少米.设甲工程队每天施工x米,乙工程队每天施工y米,根据题意,列出方程组 .
14.我国古代问题:以绳测井,若将绳三折测之,绳多四尺,若将绳四折测之,绳多一尺,井深几何?这段话的意思是:用绳子量井深,把绳三折来量,井外余绳四尺,把绳四折来量,井外余绳一尺,井深几尺?则该问题的井深是 尺.
三.解答题
15.列方程组解应用题:
甲乙两人从相距36千米的两地相向而行.如果甲比乙先走2小时,那么在乙出发后3小时相遇;如果乙比甲先走2小时,那么在甲出发后2.5小时相遇.甲、乙两人每小时各走多少千米?
16.某旅行社组织一批游客外出旅游,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满.已知45座客车租金为每辆220元,60座客车租金为每辆300元,问:
(1)这批游客的人数是多少?原计划租用多少辆45座客车?
(2)若租用同一种车,要使每位游客都有座位,应该怎样租用才合算?
17.某商场新进一种服装,每套服装售价100元,若将裤子降价10%,上衣涨价5%,调价后这套服装的单价和比原来提高了2%,这套服装原来裤子和上衣的单价分别是多少?
18.在矩形ABCD中,放入六个形状、大小相同的长方形,所标尺寸如图所示.试求图中阴影部分的总面积(写出分步求解的简明过程)
19.某铁件加工厂用如图1的长方形和正方形铁片(长方形的宽与正方形的边长相等)加工成如图2的竖式与横式两种无盖的长方体铁容器.(加工时接缝材料不计)
(1)如果加工竖式铁容器与横式铁容器各1个,则共需要长方形铁片 张,正方形铁片 张;
(2)现有长方形铁片2014张,正方形铁片1176张,如果加工成这两种铁容器,刚好铁片全部用完,那加工的竖式铁容器、横式铁容器各有多少个?
(3)把长方体铁容器加盖可以加工成为铁盒.现用35张铁板做成长方形铁片和正方形铁片,已知每张铁板可做成3个长方形铁片或4个正方形铁片,也可以将一张铁板裁出1个长方形铁片和2个正方形铁片.该如何充分利用这些铁板加工成铁盒,最多可以加工成多少个铁盒?
20.甲乙两个施工队在六安(六盘水﹣安顺)城际高铁施工中,每天甲队比乙队多铺设100米钢轨,甲队铺设5天的距离刚好等于乙队铺设6天的距离.若设甲队每天铺设x米,乙队每天铺设y米.
(1)依题意列出二元一次方程组;
(2)求出甲乙两施工队每天各铺设多少米?
参考答案
一.选择题
1.解:∵设哈密瓜每千克x元,青提葡萄每千克y元,得方程x+2y=70,
∴当y=36时,x=﹣2,此种情况不合实际,故选选项A不正确;
当x=12时,12+2y=70,解得y=29,故选项B不正确;
若是方程x+2y=70的解,则m,n不一定可以表示哈密瓜、青提葡萄的单价,如m=﹣2,n=36,故选项C不正确;
若m,n分别表示哈密瓜、青提葡萄的单价,则m,n一定是方程x+2y=70的解,故选项D正确;
故选:D.
2.解:设欢欢答对了x道题,答错了y道题,则:
5x﹣3y﹣(20﹣x﹣y)=72,
整理得:6x﹣2y=92.
故选:C.
3.解:根据题意得:
轿车行驶2小时的路程为:2a,
卡车行驶3小时的路程为:3b,
∵轿车行驶2小时的路程比卡车行驶3小时的路程少40千米,
∴3b﹣2a=40,
整理得:3b=2a+40,2a=3b﹣40,
故选:C.
4.解:根据总天数是60天,可得x+y=60;根据乙种零件应是甲种零件的2倍,可列方程为2×24x=12y.
则可列方程组为.
故选:C.
5.解:设清酒x斗,醑酒y斗,
依题意得:.
故选:A.
二.填空题
6.解:根据图示可得,
故答案是:.
7.解:设较长铁棒的长度为xcm,较短铁棒的长度为ycm.
因为两根铁棒之和为55cm,故可列x+y=55,
又知两棒未露出水面的长度相等,故可知x=y,
据此可列:,
解得:,
因此木桶中水的深度为30×=20cm.
故填20.
8.解:设小林自己走的路程为S.
根据题意得:=+40=+40=50(分钟).
故填50.
9.解:由题意可得,
6x+4y=50,
故答案为:6x+4y=50.
10.解:设桌子的高度为xcm,长方体木块一个面(图中展示的面)的长比宽大ycm,
依题意得:,
解得:.
故答案为:75.
11.解:设每块墙砖的长为xcm,宽为ycm,
依题意得:,
解得:,
∴xy=45×20=900(cm2).
故答案为:900.
12.解:设这艘船在静水中的速度和水流速度分别为x千米/小时,y千米/小时,
依题意得,
解得:,
答:这艘船在静水中的速度为17千米/小时,
故答案为:17.
13.解:由题意可得,
,
故答案是:.
14.解:设绳长是x尺,井深是y尺,依题意有
,
解得,.
故井深是8尺.
故答案为:8.
三.解答题
15.解:设甲,乙速度分别为x,y千米/时,
,
解得:,
甲的速度是3.6千米每小时,乙的速度是6千米每小时.
16.解:(1)设这批游客的人数是x人,原计划租用45座客车y辆.
根据题意,得,
解这个方程组,得.
答:这批游客的人数240人,原计划租45座客车5辆;
(2)租45座客车:240÷45≈5.3(辆),所以需租6辆,租金为220×6=1320(元),
租60座客车:240÷60=4(辆),所以需租4辆,租金为300×4=1200(元).
答:租用4辆60座客车更合算.
17.解:设裤子单价是x元,上衣原来的单价是y元,
依题意得:,
解得:.
答:这套服装原来裤子的单价为20元,上衣的单价是80元.
18.解:设小长方形的长为x,宽为y,如图可知,
x+3y=14,①
x+y﹣2y=6,即x﹣y=6,②
①﹣②得4y=8,y=2,代入②得x=8,
因此,大矩形ABCD的宽AD=6+2y=6+2×2=10.
矩形ABCD面积=14×10=140(平方厘米),
阴影部分总面积=140﹣6×2×8=44(平方厘米).
19.解:(1)如果加工竖式铁容器与横式铁容器各1个,则共需要长方形铁片7张,正方形铁片3张;
(2)设加工的竖式铁容器有x个,横式铁容器有y个,根据题意得,
解得
答:竖式铁容器加工100个,横式铁容器加工538个;
(3)设做长方形铁片的铁板为m块,做正方形铁片的铁板为n块,
依题意,得:,
解得:.
∵在这35块铁板中,25块做长方形铁片可做25×3=75(张),9块做正方形铁片可做9×4=36(张),剩下1块可裁出1张长方形铁片和2张正方形铁片,
∴共做长方形铁片75+1=76(张),正方形铁片36+2=38(张),
∴可做铁盒76÷4=19(个).
答:最多可以加工成19个铁盒.
20.解:(1)∵甲队每天铺设x米,乙队每天铺设y米,每天甲队比乙队多铺设100米钢轨,甲队铺设5天的距离刚好等于乙队铺设6天的距离,
∴.
(2),
解得:.
答:甲队每天铺设600米,乙队每天铺设500米.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
