4.5 三角形的中位线 同步练习(含答案)
文档属性
| 名称 | 4.5 三角形的中位线 同步练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
4.5 三角形的中位线
知识点1 三角形中位线定理
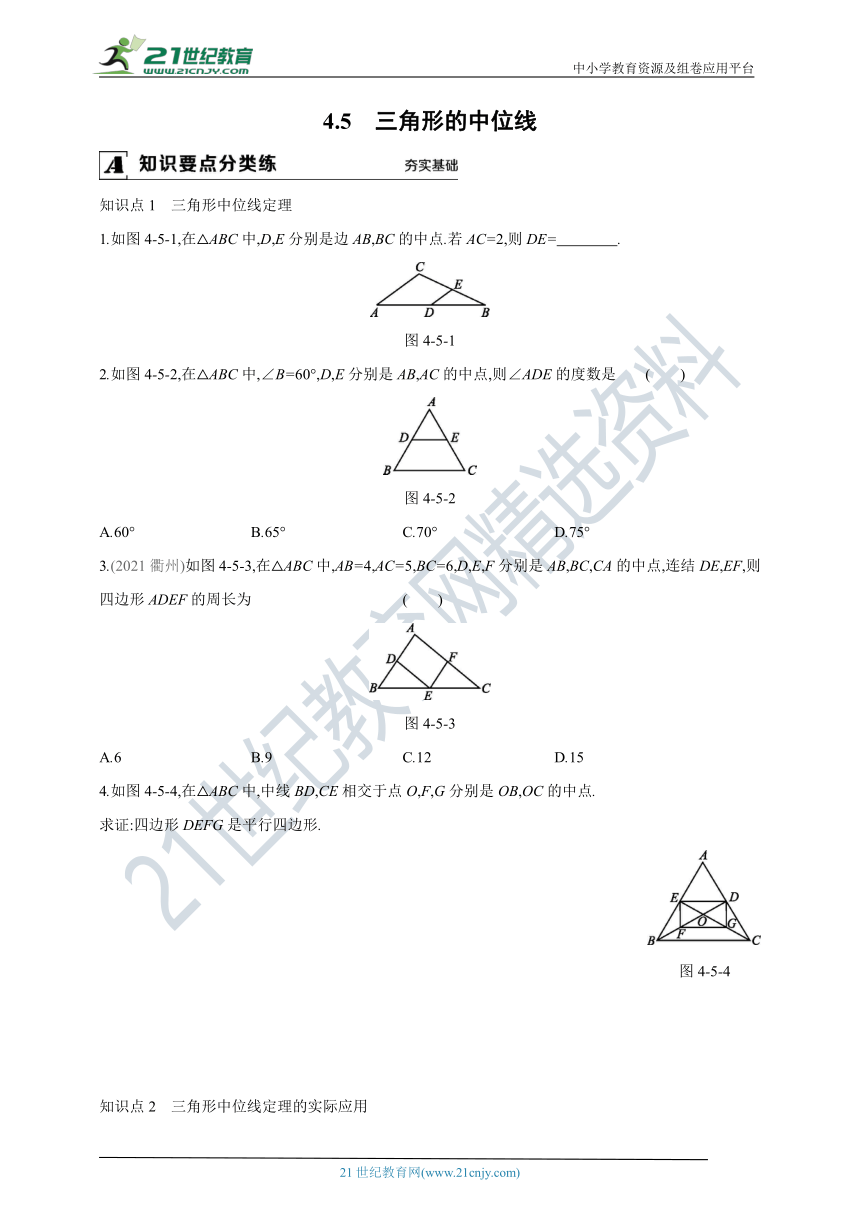
1.如图4-5-1,在△ABC中,D,E分别是边AB,BC的中点.若AC=2,则DE= .
图4-5-1
2.如图4-5-2,在△ABC中,∠B=60°,D,E分别是AB,AC的中点,则∠ADE的度数是 ( )
图4-5-2
A.60° B.65° C.70° D.75°
3.(2021衢州)如图4-5-3,在△ABC中,AB=4,AC=5,BC=6,D,E,F分别是AB,BC,CA的中点,连结DE,EF,则四边形ADEF的周长为 ( )
图4-5-3
A.6 B.9 C.12 D.15
4.如图4-5-4,在△ABC中,中线BD,CE相交于点O,F,G分别是OB,OC的中点.
求证:四边形DEFG是平行四边形.
图4-5-4
知识点2 三角形中位线定理的实际应用
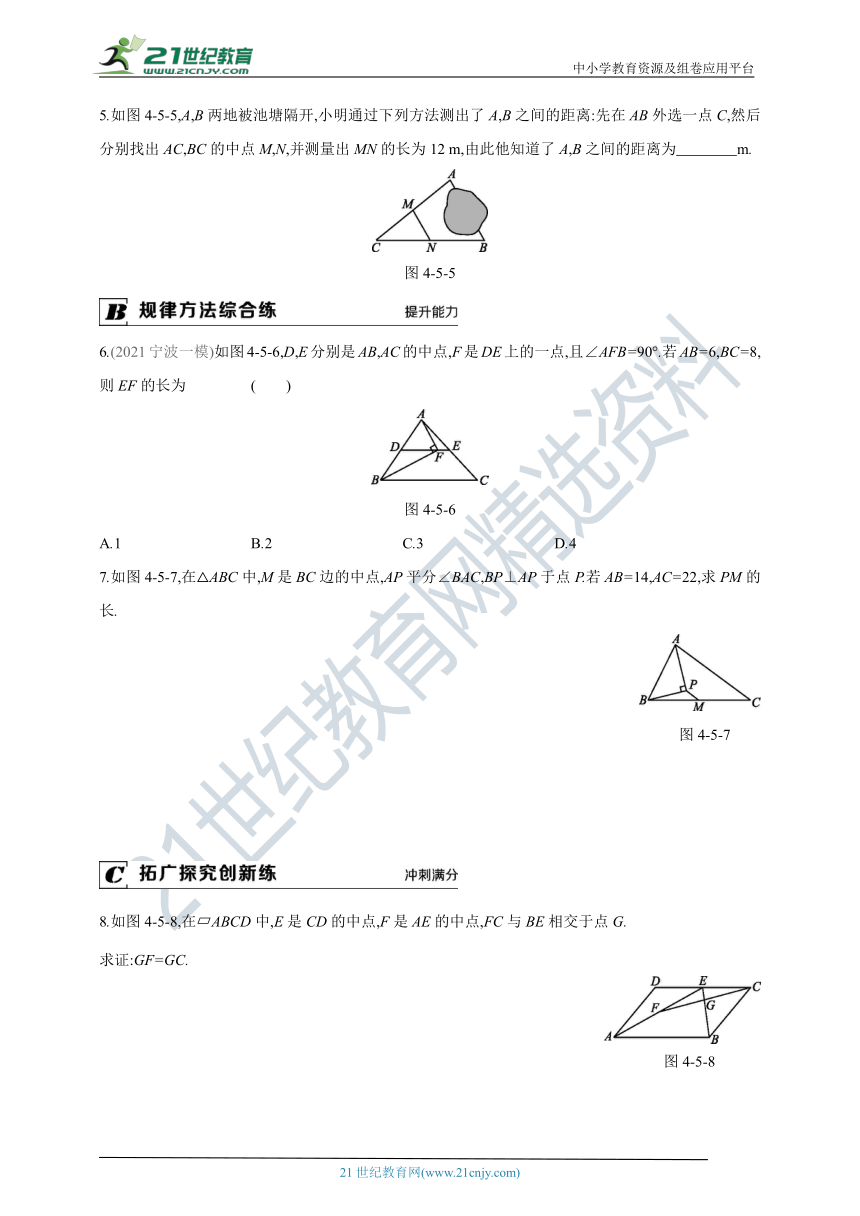
5.如图4-5-5,A,B两地被池塘隔开,小明通过下列方法测出了A,B之间的距离:先在AB外选一点C,然后分别找出AC,BC的中点M,N,并测量出MN的长为12 m,由此他知道了A,B之间的距离为 m.
图4-5-5
6.(2021宁波一模)如图4-5-6,D,E分别是AB,AC的中点,F是DE上的一点,且∠AFB=90°.若AB=6,BC=8,则EF的长为 ( )
图4-5-6
A.1 B.2 C.3 D.4
7.如图4-5-7,在△ABC中,M是BC边的中点,AP平分∠BAC,BP⊥AP于点P.若AB=14,AC=22,求PM的长.
图4-5-7
8.如图4-5-8,在 ABCD中,E是CD的中点,F是AE的中点,FC与BE相交于点G.
求证:GF=GC.
图4-5-8
详解详析
1.1 2.A
3.B [解析] ∵D,E,F分别是AB,BC,CA的中点,
∴DE=AC=2.5,AF=AC=2.5,EF=AB=2,AD=AB=2,
∴四边形ADEF的周长=AD+DE+EF+AF=9.
故选B.
4.证明:∵BD,CE是△ABC的中线,
∴E,D分别是AB,AC的中点,
∴ED是△ABC的中位线,
∴EDBC.
∵F,G分别是OB,OC的中点,
∴FG是△OBC的中位线,
∴FGBC,则FG ED,
∴四边形DEFG是平行四边形.
5.24
6.A [解析] ∵D,E分别是AB,AC的中点,
∴DE是△ABC的中位线.
∵BC=8,
∴DE=BC=4.
∵∠AFB=90°,D是AB的中点,AB=6,
∴DF=AB=3,
∴EF=DE-DF=4-3=1.
故选A.
7.解:如图,延长BP交AC于点H.
∵AP⊥BH,
∴∠APB=∠APH=90°.
∵AP平分∠BAC,
∴∠PAB=∠PAH.
又∵AP=AP,∴△ABP≌△AHP,
∴AH=AB=14,BP=HP.
又∵M是BC边的中点,
∴PM是△BCH的中位线,
∴PM=CH=×(22-14)=4.
8.证明:如图,取EB的中点H,连结FH,CH.
又∵F是AE的中点,
∴FH是△ABE的中位线,
∴FH∥AB,
FH=AB.
∵在 ABCD中,E是CD的中点,
∴CE∥AB,CE=CD,AB=CD,
∴CE∥FH,CE=FH,
∴四边形EFHC是平行四边形,∴GF=GC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
4.5 三角形的中位线
知识点1 三角形中位线定理
1.如图4-5-1,在△ABC中,D,E分别是边AB,BC的中点.若AC=2,则DE= .
图4-5-1
2.如图4-5-2,在△ABC中,∠B=60°,D,E分别是AB,AC的中点,则∠ADE的度数是 ( )
图4-5-2
A.60° B.65° C.70° D.75°
3.(2021衢州)如图4-5-3,在△ABC中,AB=4,AC=5,BC=6,D,E,F分别是AB,BC,CA的中点,连结DE,EF,则四边形ADEF的周长为 ( )
图4-5-3
A.6 B.9 C.12 D.15
4.如图4-5-4,在△ABC中,中线BD,CE相交于点O,F,G分别是OB,OC的中点.
求证:四边形DEFG是平行四边形.
图4-5-4
知识点2 三角形中位线定理的实际应用
5.如图4-5-5,A,B两地被池塘隔开,小明通过下列方法测出了A,B之间的距离:先在AB外选一点C,然后分别找出AC,BC的中点M,N,并测量出MN的长为12 m,由此他知道了A,B之间的距离为 m.
图4-5-5
6.(2021宁波一模)如图4-5-6,D,E分别是AB,AC的中点,F是DE上的一点,且∠AFB=90°.若AB=6,BC=8,则EF的长为 ( )
图4-5-6
A.1 B.2 C.3 D.4
7.如图4-5-7,在△ABC中,M是BC边的中点,AP平分∠BAC,BP⊥AP于点P.若AB=14,AC=22,求PM的长.
图4-5-7
8.如图4-5-8,在 ABCD中,E是CD的中点,F是AE的中点,FC与BE相交于点G.
求证:GF=GC.
图4-5-8
详解详析
1.1 2.A
3.B [解析] ∵D,E,F分别是AB,BC,CA的中点,
∴DE=AC=2.5,AF=AC=2.5,EF=AB=2,AD=AB=2,
∴四边形ADEF的周长=AD+DE+EF+AF=9.
故选B.
4.证明:∵BD,CE是△ABC的中线,
∴E,D分别是AB,AC的中点,
∴ED是△ABC的中位线,
∴EDBC.
∵F,G分别是OB,OC的中点,
∴FG是△OBC的中位线,
∴FGBC,则FG ED,
∴四边形DEFG是平行四边形.
5.24
6.A [解析] ∵D,E分别是AB,AC的中点,
∴DE是△ABC的中位线.
∵BC=8,
∴DE=BC=4.
∵∠AFB=90°,D是AB的中点,AB=6,
∴DF=AB=3,
∴EF=DE-DF=4-3=1.
故选A.
7.解:如图,延长BP交AC于点H.
∵AP⊥BH,
∴∠APB=∠APH=90°.
∵AP平分∠BAC,
∴∠PAB=∠PAH.
又∵AP=AP,∴△ABP≌△AHP,
∴AH=AB=14,BP=HP.
又∵M是BC边的中点,
∴PM是△BCH的中位线,
∴PM=CH=×(22-14)=4.
8.证明:如图,取EB的中点H,连结FH,CH.
又∵F是AE的中点,
∴FH是△ABE的中位线,
∴FH∥AB,
FH=AB.
∵在 ABCD中,E是CD的中点,
∴CE∥AB,CE=CD,AB=CD,
∴CE∥FH,CE=FH,
∴四边形EFHC是平行四边形,∴GF=GC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
