2021-2022学年浙教版八年级数学下册2.3一元二次方程的应用之动态几何问题解答题专题训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年浙教版八年级数学下册2.3一元二次方程的应用之动态几何问题解答题专题训练(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 221.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-18 00:00:00 | ||
图片预览



文档简介
2021-2022学年浙教版八年级数学下册《2-3一元二次方程的应用之动态几何问题》
解答题专题训练(附答案)
1.如图A,B,C,D为矩形的四个顶点,AB=16cm,AD=6cm,动点P,Q分别从点A,C同时出发,点P以3cm/s的速度向点B移动,一直到达B点为止,点Q以2m/s的速度向D点移动,当点P到达B点时点Q随之停止运动.
(1)AP= ,BP= ,CQ= ,DQ= (用含t的代数式表示);
(2)t为多少时,四边形PBCQ的面积为33cm2;
(3)t为多少时,点P和点Q的距离为10cm.
2.如图,在Rt△ABC中,∠C=90°,AC=12cm,BC=9cm.现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB向点B方向运动,如果点P的速度是2cm/s,点Q的速度是1cm/s,它们同时出发,当有一点到达所在线段的端点时,就停止运动.设运动的时间为ts,Rt△CPQ的面积Scm2.
(1)用含t的代数式表示S.
(2)当运动多少秒时,Rt△CPQ的面积等于5cm2?
3.如图,△ABC中,∠C=90°,AC=3cm,BC=4cm,动点P从点B出发以2cm/s的速度向点C移动,同时动点Q从点C出发以1cm/s的速度向点A移动,其中一点到达终点后另一点也随之停止运动,设它们的运动时间为ts.
(1)运动几秒时,△CPQ为等腰三角形?
(2)t为何值时,△CPQ的面积等于△ABC面积的?
(3)在运动过程中,PQ的长度能否为1cm?试说明理由.
4.如图,在梯形ABCD中,AD∥BC,∠C=∠D=90°,BC=16,CD=12,AD=21.动点P从点D出发,沿线段DA的方向以每秒2个单位长度的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长度的速度向点B运动.点P,Q分别从点D,C同时出发,当点P运动到点A时,点Q随之停止运动.设运动时间为t(s),当t为何值时,以B,P,Q三点为顶点的三角形为等腰三角形?
5.已知:如图,△ABC是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间t(s),解答下列各问题:
(1)经过秒时,求△PBQ的面积;
(2)当t为何值时,△PBQ是直角三角形?
(3)是否存在某一时刻t,使四边形APQC的面积是△ABC面积的三分之二?如果存在,求出t的值;不存在请说明理由.
6.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:
(1)经过多少时间,△AMN的面积等于矩形ABCD面积的?
(2)是否存在时间t,使△AMN的面积达到3.5cm2?若存在,求出时间t;若不存在,说明理由.
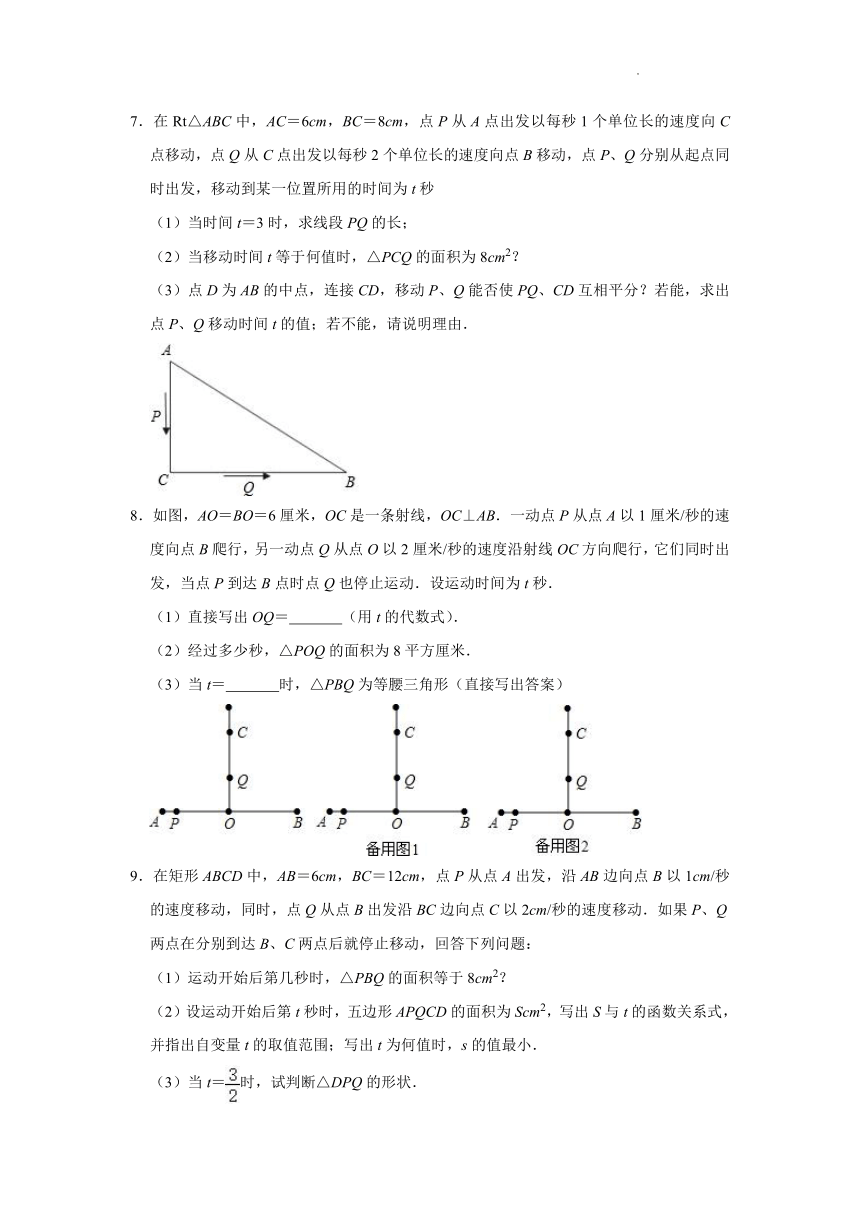
7.在Rt△ABC中,AC=6cm,BC=8cm,点P从A点出发以每秒1个单位长的速度向C点移动,点Q从C点出发以每秒2个单位长的速度向点B移动,点P、Q分别从起点同时出发,移动到某一位置所用的时间为t秒
(1)当时间t=3时,求线段PQ的长;
(2)当移动时间t等于何值时,△PCQ的面积为8cm2?
(3)点D为AB的中点,连接CD,移动P、Q能否使PQ、CD互相平分?若能,求出点P、Q移动时间t的值;若不能,请说明理由.
8.如图,AO=BO=6厘米,OC是一条射线,OC⊥AB.一动点P从点A以1厘米/秒的速度向点B爬行,另一动点Q从点O以2厘米/秒的速度沿射线OC方向爬行,它们同时出发,当点P到达B点时点Q也停止运动.设运动时间为t秒.
(1)直接写出OQ= (用t的代数式).
(2)经过多少秒,△POQ的面积为8平方厘米.
(3)当t= 时,△PBQ为等腰三角形(直接写出答案)
9.在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以1cm/秒的速度移动,同时,点Q从点B出发沿BC边向点C以2cm/秒的速度移动.如果P、Q两点在分别到达B、C两点后就停止移动,回答下列问题:
(1)运动开始后第几秒时,△PBQ的面积等于8cm2?
(2)设运动开始后第t秒时,五边形APQCD的面积为Scm2,写出S与t的函数关系式,并指出自变量t的取值范围;写出t为何值时,s的值最小.
(3)当t=时,试判断△DPQ的形状.
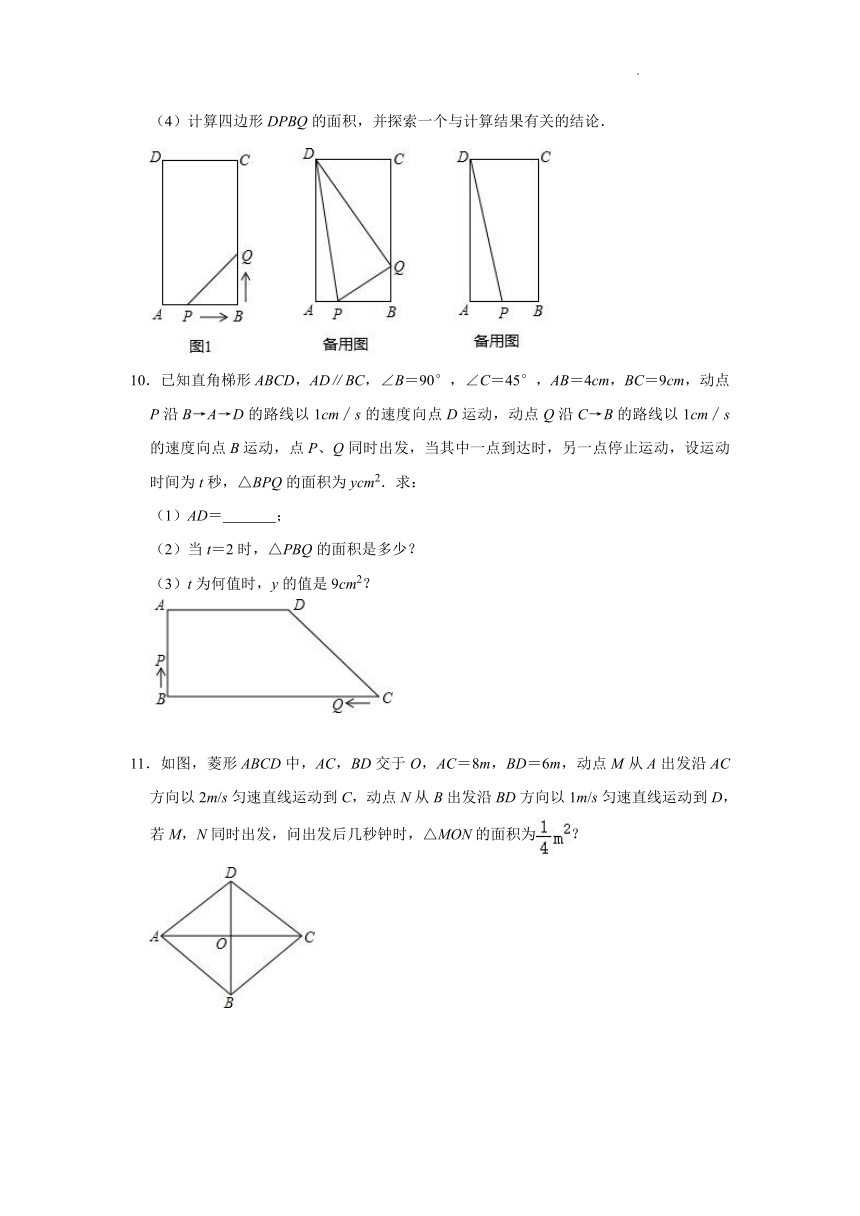
(4)计算四边形DPBQ的面积,并探索一个与计算结果有关的结论.
10.已知直角梯形ABCD,AD∥BC,∠B=90°,∠C=45°,AB=4cm,BC=9cm,动点P沿B→A→D的路线以1cm∕s的速度向点D运动,动点Q沿C→B的路线以1cm∕s的速度向点B运动,点P、Q同时出发,当其中一点到达时,另一点停止运动,设运动时间为t秒,△BPQ的面积为ycm2.求:
(1)AD= ;
(2)当t=2时,△PBQ的面积是多少?
(3)t为何值时,y的值是9cm2?
11.如图,菱形ABCD中,AC,BD交于O,AC=8m,BD=6m,动点M从A出发沿AC方向以2m/s匀速直线运动到C,动点N从B出发沿BD方向以1m/s匀速直线运动到D,若M,N同时出发,问出发后几秒钟时,△MON的面积为?
12.如图:已知正方形ABCD的边长为2cm,现在两动点P、Q分别从顶点B、A同时出发,当P沿线段BA以1cm/s的速度向点A运动,点Q沿折线A→D→C以2cm/s的速度向C运动.设点P、Q运动的时间为t(秒)
(1)当t为何值时,线段PQ与BC平行?
(2)设1≤t<2,当t为何值时,线段PQ将正方形ABCD的面积分为2:3两部分?
13.△ABC中,∠A=90°,∠C=30°,AB=1,两个动点P和Q同时从点A出发,P沿AC运动,Q沿AB,BC运动,结果两个动点同时到达点C.
(1)点Q的速度是点P速度的几倍?
(2)当AP为何值时,△APQ的面积为?
14.探究:如图.已知矩形OABC,顶点A、C分别在x、y 轴的正半轴上,点B的坐标为(8,4),M是BC的中点.动点P、Q同时从点O出发.分别沿线段OC和OA向点C和点A运动(任一点到达目的后两动点同时停止运动).点P的速度为1个单位/秒,点Q的速度为2个单位/秒.设运动的时间为t秒.求当t为何值时,△MPQ的面积为5平方单位?
15.如图,面积为50的等腰直角△ABC中,P为斜边上一动点,PQ⊥AC于Q,连接PC,求当动点P运动到恰好使△PCQ的面积为10时,△PCQ的周长.
16.如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,动点D从点A出发以4cm/s速度向点C移动,同时动点E从C出发以3cm/s的速度向点B移动,设它们的运动时间为ts.
(1)根据题意知:CE= ,CD= ;(用含t的代数式表示)
(2)t为何值时,△CDE的面积等于四边形ABED的面积的?
(3)点D、E运动时,DE的长可以是4cm吗?如果可以,请求出t的值,如果不可以,请说明理由.
17.如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A出发,以1cm/s的速度沿AB边向点B移动,以此同时,点Q从点C出发,以2cm/s的速度沿CB边向点B移动,如果P,Q同时出发,经过几秒,△PBQ的面积等于8cm2?
18.如图,在边长为12cm的等边三角形ABC中,点P从点A开始沿AB边向点B以每秒钟1cm的速度移动,点Q从点B开始沿BC边向点C以每秒钟2cm的速度移动.若P、Q分别从A、B同时出发,其中任意一点到达目的地后,两点同时停止运动,求:
(1)经过6秒后,BP= cm,BQ= cm;
(2)经过几秒后,△BPQ是直角三角形?
(3)经过几秒△BPQ的面积等于cm2?
19.如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?
(1)请你将小明对“思考题”的解答补充完整:
解:设点B将向外移动x米,即BB1=x,
则B1C=x+0.7,A1C=AC﹣AA1=﹣0.4=2
而A1B1=2.5,在Rt△A1B1C中,由B1C2+A1C2=A1B12得方程 ,
解方程得x1= ,x2= ,∴点B将向外移动 米.
(2)解完“思考题”后,小聪提出了如下问题:
梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?请你解答小聪提出的这个问题.
20.在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时点Q从点B沿边BC向点C以2cm/s的速度移动,设运动时间为t.
(1)问几秒后△PBQ的面积等于8cm2?
(2)是否存在t,使△PDQ的面积等于26cm2?
参考答案
1.解:(1)当运动时间为ts时,AP=3tcm,BP=(16﹣3t)cm,CQ=2tcm,DQ=(16﹣2t)cm.
故答案为:3tcm;(16﹣3t)cm;2tcm;(16﹣2t)cm.
(2)依题意得:[(16﹣3t)+2t]×6=33,
整理得:16﹣t=11,
解得:t=5.
答:当t为5时,四边形PBCQ的面积为33cm2.
(3)过点Q作QE⊥AB于点E,则PE=|(16﹣3t)﹣2t|=|16﹣5t|,如图所示.
依题意得:|16﹣5t|2+62=102,
即(16﹣5t)2=82,
解得:t1=,t2=.
答:当t为或时,点P和点Q的距离为10cm.
2.解:(1)由题意得:CP=AC﹣2t,CQ=t,
∴S=CP CQ=(AC﹣2t)t,
∵AC=12cm,BC=9cm,
∴S=(12﹣2t)t=﹣t2+6t;
(2)当S=5cm2时,
﹣t2+6t=5,
解得:t1=1,t2=5,
即当t=1或t=5时,Rt△CPQ的面积等于5cm2.
3.解:经过t秒后,PC=(4﹣2t)cm,CQ=tcm,
(1)若△CPQ为等腰三角形,
则PC=CQ,即4﹣2t=t,
解得:t=,
∴运动秒时,△CPQ为等腰三角形;
(2)当△CPQ的面积等于△ABC面积的时,
即×(4﹣2t) t=××3×4,
整理得:4t2﹣8t+3=0,
解得:t1=,t2=,
∴经过或秒后,△CPQ的面积等于△ABC面积的;
(3)∵∠C=90°,
∴(4﹣2t)2+t2=1,
整理得:5t2﹣16t+15=0,
∵Δ=162﹣4×5×15=256﹣300=﹣44<0,
∴此方程无实数解,
∴在运动过程中,PQ的长度不能为1cm.
4.解:如图1,当PB=PQ时,作PE⊥BC于E,
∴EQ=BQ,
∵CQ=t,
∴BQ=16﹣t,
∴EQ=8﹣t,
∴EC=8﹣t+t=8+t.
∴2t=8+t.
解得:t=.
如图2,当PQ=BQ时,作QE⊥AD于E,
∴∠PEQ=∠DEQ=90°,
∵∠C=∠D=90°,
∴∠C=∠D=∠DEQ=90°,
∴四边形DEQC是矩形,
∴DE=QC=t,
∴PE=t,QE=CD=12.
在Rt△PEQ中,由勾股定理,得
PQ=.
16﹣t=,
解得:t=;
如图3,当BP=BQ时,作PE⊥BC于E,
∵CQ=t,
∴BP=BQ=BC﹣CQ=16﹣t,
∵PD=2t,
∴CE=2t,
∴BE=16﹣2t,
在Rt△BEP中,
(16﹣2t)2+122=(16﹣t)2,
3t2﹣32t+144=0,
△=(﹣32)2﹣4×3×144=﹣704<0,
故方程无解.
综上所述,t=或时,以B,P,Q三点为顶点的三角形为等腰三角形.
5.解:(1)经过秒时,AP=cm,BQ=cm,
∵△ABC是边长为3cm的等边三角形,
∴AB=BC=3cm,∠B=60°,
∴BP=3﹣=cm,
∴△PBQ的面积=;
(2)设经过t秒△PBQ是直角三角形,
则AP=tcm,BQ=tcm,
△ABC中,AB=BC=3cm,∠B=60°,
∴BP=(3﹣t)cm,
△PBQ中,BP=(3﹣t)cm,BQ=tcm,若△PBQ是直角三角形,则∠BQP=90°或∠BPQ=90°,
当∠BQP=90°时,BQ=BP,
即t=(3﹣t),t=1(秒),
当∠BPQ=90°时,BP=BQ,
3﹣t=t,t=2(秒),
答:当t=1秒或t=2秒时,△PBQ是直角三角形.
(3)过P作PM⊥BC于M,
∴PM=(3﹣t),
∴S△PBQ=BQ PM= t (3﹣t),
∴y=S△ABC﹣S△PBQ=×32×﹣×t×(3﹣t)
=t2﹣t+,
∴y与t的关系式为y=t2﹣t+,
假设存在某一时刻t,使得四边形APQC的面积是△ABC面积的,
则S四边形APQC=S△ABC,
∴t2﹣t+=××32×,
∴t2﹣3t+3=0,
∵(﹣3)2﹣4×1×3<0,
∴方程无解,
∴无论t取何值,四边形APQC的面积都不可能是△ABC面积的.
6.解:(1)设经过ts,△AMN的面积等于矩形ABCD面积的,则DN=2tcm,AM=tcm,AN=AD﹣DN=(6﹣2t)cm,
∴AN AM=AD AB,即(6﹣2t)t=×6×3,
整理得:t2﹣3t+2=0,即(t﹣1)(t﹣2)=0,
解得:t1=1,t2=2,
则经过1s或2s,△AMN的面积等于矩形ABCD面积的;
(2)不存在,理由为:假设存在时间ts,使△AMN的面积达到3.5cm2,
则AN AM=3.5,
整理得:2t2﹣6t+7=0,
∵Δ=36﹣56=﹣20<0,
∴方程没有实数根,
则△AMN的面积不能达到3.5cm2.
7.解:(1)∵AP=t,CQ=2t,
∴t=3时,AP=3,CQ=6,
∴PC=6﹣3=3
在Rt△PCQ中,由勾股定理,得
PQ==3.
答:PQ=3;
(2)∵AP=t,CQ=2t,
∴PC=6﹣t.
∴(6﹣t)×2t=8,
解得:t1=2,t2=4.
(3)PQ、CD不互相平分.
当PQ、CD互相平分,
∴四边形PCQD是平行四边形,
∴PD∥CQ.PD=CQ.
∵点D为AB的中点,
∴P是AC的中点,
∴AP=AC=3,PD=CQ=BC=4.
∴t=≠.
∴PQ、CD不互相平分.
8.解:(1)由函数图象,得
OQ=2t,
故答案为:2t;
(2)当P在AO上,
,
解得:t1=2,t2=4.
∵t1=2,t2=4在0<t<6范围内,
∴t1=2,t2=4.
P在BO上,
=8,
解得:t3=3+,t4=3﹣.
∵t3=3+在6<t<12范围内,
∴t3=3+;
(3)在Rt△BOQ中,由勾股定理,得
BQ2=4t2+36,
BP=12﹣t,BP2=144﹣24t+t2,
∵△PBQ是等腰三角形,
∴PB=BQ,
∴PB2=BQ2,
∴4t2+36=144﹣24t+t2,
解得:t1=﹣4+2,t2=﹣4﹣2(舍去).
当PB=PQ时,BP2=144﹣24t+t2,PQ2=4t2+(6﹣t)2,
t1=,t2=(舍去).
故答案为:﹣4+2或.
9.解:(1)设经过t秒,△PBQ的面积等于8cm2则:
BP=6﹣t,BQ=2t,
所以S△PBQ=×(6﹣t)×2t=8,即t2﹣6t+8=0,
可得:t=2或4,即经过2秒或4秒,△PBQ的面积等于8cm2.
(2)根据(1)中所求出的S△PBQ=PB BQ=×(6﹣t)×2t,
整理得S△PBQ=﹣t2+6t(0<t<6).
则S五边形APQCD=S矩形ABCD﹣S△PBQ=72﹣(﹣t2+6t)=t2﹣6t+72=(t﹣3)2+63(0<t<6),
当t=﹣=3时,S五边形APQCD=63,
故当t=3秒,五边形APQCD的面积最小,最小值是63cm2,
(3)当t=1.5s时,
AP=1.5,BP=4.5,CQ=9,
∴DP2=146.25,PQ2=29.25,DQ2=117,
∴PQ2+DQ2=DP2,
∴△DPQ为Rt△;
(4)SDPBQ=6×12﹣t×12﹣×6(12﹣2t),
=72﹣36,
=36,
∴四边形DPBQ的面积是固定值36.
10.解:(1)过D点作DE⊥BC与E.
∵∠B=90°,
∴AB∥DE,
∵AD∥BC,
∴四边形ABED是矩形,
∴AD=BE,AB=DE,
∵∠C=45°,
∴EC=DE=4cm,
∴AD=BE=BC﹣EC=5cm;
(2)当t=2时,BP=2cm,BQ=9﹣2=7cm,
△PBQ的面积=2×7÷2=7cm2;
(3)P点在AB上时,t(9﹣t)÷2=9,解得t1=3,t2=6(不合题意舍去);
P点在AD上,4(9﹣t)÷2=9,解得t=4.5.
故t=3或4.5时,y的值是9cm2.
故答案为:5cm.
11.解:设出发后x秒时,
(1)当x<2时,点M在线段AO上,点N在线段BO上.(4﹣2x)(3﹣x)=;
解得x1=,x2=
∵x<2,
∴;
(2)当2<x<3时,点M在线段OC上,点N在线段BO上,(2x﹣4)(3﹣x)=;
解得;
(3)当3<x≤4时,点M在线段OC上,点N在线段OD上,(2x﹣4)(x﹣3)=;
解得x1=s或x2=s.
综上所述,出发后或s或时,△MON的面积为.
12.解:由题意,得
2t﹣2=2﹣t,
解得:t=.
答:t=s时,线段PQ与BC平行;
(2)∵正方形的边长为2cm,
∴正方形的面积为:4cm2.
∴PQ分得的两部分的面积分别为:cm2,cm2.
如图1,当S△PAQ=时,
(2﹣t)2t×=,
5t2﹣10t+8=0,Δ<0,此方程无解.
如图2,当四边形APQD=时,
=,
解得:t=.
如图2,当四边形APQD=时,
=,
解得:t=>2(舍去).
∴当t=时,线段PQ将正方形ABCD的面积分为2:3两部分.
13.解:(1)∵在△ABC中,∠A=90°,∠C=30°,AB=1,
∴BC=2,AC=,
∵两个动点P,Q同时从A点出发,点P沿AC运动,点Q沿AB,BC运动,两点同时到达点C
∴Q的速度是P的速度的(2+1)÷=倍;
(2)设AP=x,由(1)知Q点运动路程为x,
①点Q在AB上运动,0≤≤1,即0≤x≤,
当点Q与点B重合时,△APQ的面积最大;
此时AQ=AB=1,则AP=,
故△APQ的面积为:=<;
②点Q在BC上运动,1<≤3,即<x≤;
如图所示,过点Q作QM⊥AC,垂足为M,
则CQ=3﹣x,
∵在△ABC中,∠A=90°,∠C=30°,
∴QM=CQ=,
根据题意,得:,
解得:x=(符合题意).
答:当AP为时,△APQ的面积为.
14.解:设t秒时,△MPQ的面积为5平方单位,
由题意可得:PC=4﹣t,PO=t,QO=2t,AQ=8﹣2t,BM=CM=4,AB=4,
故S△PMQ=S矩形ABCO﹣S△OPQ﹣S△PCM﹣S梯形AQBM
5=4×8﹣t 2t﹣(4﹣t) 4﹣(4+8﹣2t)×4
整理得:t2﹣6t+5=0,
解得:t1=1,t2=5(不合题意舍去),
答:当t为1秒时,△MPQ的面积为5平方单位.
15.解:设AC=x,则BC=x.
∵等腰直角△ABC的面积为50,
∴x2=50,
解得x=±10(负值舍去),
∴AC=BC=10.
设PQ=y,则AQ=y,CQ=10﹣y.
∵△PCQ的面积为10,
∴y(10﹣y)=10,
解得y=5±,
当y=5+时,PQ=5+,CQ=5﹣,PC==2;
当y=5﹣时,PQ=5﹣,CQ=5+,PC==2;
∴△PCQ的周长=PQ+CQ+PC=10+PC=10+2.
16.解:(1)∵动点D、E同时出发,动点E从C出发向点B移动,
∴CE=3tcm,
∵动点D从点A出发向点C移动,
∴CD=(8﹣4t)cm,
故答案为:3tcm,(8﹣4t)cm.
(2)当△CDE的面积等于四边形ABED的面积的时,则△CDE的面积等于△ABC的面积的,
根据题意得×3t(8﹣4t)=××8×6,
整理得t2﹣2t+1=0,
解得t1=t2=1,
答:t=1,即运动1秒时,△CDE的面积等于四边形ABED的面积的.
(3)不可以,理由如下:
如果可以,则由勾股定理得(3t)2+(8﹣4t)2=42,
整理得25t2﹣64t+48=0,
∵Δ=(﹣64)2﹣4×25×48=﹣704<0,
∴该方程没有实数根,
∴DE的长不可以是4cm.
17.解:设xs后,可使△PBQ的面积为8cm2.
由题意得,AP=xcm,PB=(6﹣x)cm,BQ=(8﹣2x)cm,
则(6﹣x) (8﹣2x)=8,
整理,得x2﹣10x+16=0,
解得x1=2,x2=8(不合题意舍去).
所以P、Q同时出发,2s后可使△PBQ的面积为8cm2.
18.解:(1)由题意,得
AP=6cm,BQ=12cm.
∵△ABC是等边三角形,
∴AB=BC=12cm,
∴BP=12﹣6=6cm.
故答案为:6、12.
(2)∵△ABC是等边三角形,
∴AB=BC=12cm,∠A=∠B=∠C=60°,
当∠PQB=90°时,
∴∠BPQ=30°,
∴BP=2BQ.
∵BP=12﹣x,BQ=2x,
∴12﹣x=2×2x,
∴x=,
当∠QPB=90°时,
∴∠PQB=30°,
∴BQ=2PB,
∴2x=2(12﹣x),
x=6
答6秒或秒时,△BPQ是直角三角形;
(3)作QD⊥AB于D,
∴∠QDB=90°,
∴∠DQB=30°,
∴DB=BQ=x,
在Rt△DBQ中,由勾股定理,得
DQ=x,
∴,
解得;x1=10,x2=2,
∵x=10时,2x>12,故舍去
∴x=2.
答:经过2秒△BPQ的面积等于cm2.
19.解:(1)设点B将向外移动x米,即BB1=x,
则B1C=x+0.7,A1C=AC﹣AA1=﹣0.4=2.
而A1B1=2.5,在Rt△A1B1C中,由B1C2+A1C2=A1B12得方程(x+0.7)2+22=2.52,
解方程得x1=0.8,x2=﹣2.2(不合题意舍去),∴点B将向外移动0.8m.
故答案为(x+0.7)2+22=2.52,0.8,﹣2.2(不合题意舍去),0.8;
(2)有可能.
设梯子顶端从A处下滑x米,点B向外也移动x米,
则有(x+0.7)2+(2.4﹣x)2=2.52,
解得:x1=1.7或x2=0(不合题意舍去).
故当梯子顶端从A处下滑1.7米时,点B向外也移动1.7米,即梯子顶端从A处沿墙AC下滑的距离与点B向外移动的距离有可能相等.
20.解:(1)设x秒后△PBQ的面积等于8cm2,
∵AP=x,QB=2x.
∴PB=6﹣x.
∴×(6﹣x)2x=8,
解得x1=2,x2=4,
答:2秒或4秒后△PBQ的面积等于8cm2;
(2)假设存在t使得△PDQ面积为26cm2,
则72﹣6t﹣t(6﹣t)﹣3(12﹣2t)=26,
整理得,t2﹣6t+10=0,
∵△=36﹣4×1×10=﹣4<0,
∴原方程无解,
所以不存在t,能够使△PDQ的面积等于26cm2.
解答题专题训练(附答案)
1.如图A,B,C,D为矩形的四个顶点,AB=16cm,AD=6cm,动点P,Q分别从点A,C同时出发,点P以3cm/s的速度向点B移动,一直到达B点为止,点Q以2m/s的速度向D点移动,当点P到达B点时点Q随之停止运动.
(1)AP= ,BP= ,CQ= ,DQ= (用含t的代数式表示);
(2)t为多少时,四边形PBCQ的面积为33cm2;
(3)t为多少时,点P和点Q的距离为10cm.
2.如图,在Rt△ABC中,∠C=90°,AC=12cm,BC=9cm.现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB向点B方向运动,如果点P的速度是2cm/s,点Q的速度是1cm/s,它们同时出发,当有一点到达所在线段的端点时,就停止运动.设运动的时间为ts,Rt△CPQ的面积Scm2.
(1)用含t的代数式表示S.
(2)当运动多少秒时,Rt△CPQ的面积等于5cm2?
3.如图,△ABC中,∠C=90°,AC=3cm,BC=4cm,动点P从点B出发以2cm/s的速度向点C移动,同时动点Q从点C出发以1cm/s的速度向点A移动,其中一点到达终点后另一点也随之停止运动,设它们的运动时间为ts.
(1)运动几秒时,△CPQ为等腰三角形?
(2)t为何值时,△CPQ的面积等于△ABC面积的?
(3)在运动过程中,PQ的长度能否为1cm?试说明理由.
4.如图,在梯形ABCD中,AD∥BC,∠C=∠D=90°,BC=16,CD=12,AD=21.动点P从点D出发,沿线段DA的方向以每秒2个单位长度的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长度的速度向点B运动.点P,Q分别从点D,C同时出发,当点P运动到点A时,点Q随之停止运动.设运动时间为t(s),当t为何值时,以B,P,Q三点为顶点的三角形为等腰三角形?
5.已知:如图,△ABC是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间t(s),解答下列各问题:
(1)经过秒时,求△PBQ的面积;
(2)当t为何值时,△PBQ是直角三角形?
(3)是否存在某一时刻t,使四边形APQC的面积是△ABC面积的三分之二?如果存在,求出t的值;不存在请说明理由.
6.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:
(1)经过多少时间,△AMN的面积等于矩形ABCD面积的?
(2)是否存在时间t,使△AMN的面积达到3.5cm2?若存在,求出时间t;若不存在,说明理由.
7.在Rt△ABC中,AC=6cm,BC=8cm,点P从A点出发以每秒1个单位长的速度向C点移动,点Q从C点出发以每秒2个单位长的速度向点B移动,点P、Q分别从起点同时出发,移动到某一位置所用的时间为t秒
(1)当时间t=3时,求线段PQ的长;
(2)当移动时间t等于何值时,△PCQ的面积为8cm2?
(3)点D为AB的中点,连接CD,移动P、Q能否使PQ、CD互相平分?若能,求出点P、Q移动时间t的值;若不能,请说明理由.
8.如图,AO=BO=6厘米,OC是一条射线,OC⊥AB.一动点P从点A以1厘米/秒的速度向点B爬行,另一动点Q从点O以2厘米/秒的速度沿射线OC方向爬行,它们同时出发,当点P到达B点时点Q也停止运动.设运动时间为t秒.
(1)直接写出OQ= (用t的代数式).
(2)经过多少秒,△POQ的面积为8平方厘米.
(3)当t= 时,△PBQ为等腰三角形(直接写出答案)
9.在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以1cm/秒的速度移动,同时,点Q从点B出发沿BC边向点C以2cm/秒的速度移动.如果P、Q两点在分别到达B、C两点后就停止移动,回答下列问题:
(1)运动开始后第几秒时,△PBQ的面积等于8cm2?
(2)设运动开始后第t秒时,五边形APQCD的面积为Scm2,写出S与t的函数关系式,并指出自变量t的取值范围;写出t为何值时,s的值最小.
(3)当t=时,试判断△DPQ的形状.
(4)计算四边形DPBQ的面积,并探索一个与计算结果有关的结论.
10.已知直角梯形ABCD,AD∥BC,∠B=90°,∠C=45°,AB=4cm,BC=9cm,动点P沿B→A→D的路线以1cm∕s的速度向点D运动,动点Q沿C→B的路线以1cm∕s的速度向点B运动,点P、Q同时出发,当其中一点到达时,另一点停止运动,设运动时间为t秒,△BPQ的面积为ycm2.求:
(1)AD= ;
(2)当t=2时,△PBQ的面积是多少?
(3)t为何值时,y的值是9cm2?
11.如图,菱形ABCD中,AC,BD交于O,AC=8m,BD=6m,动点M从A出发沿AC方向以2m/s匀速直线运动到C,动点N从B出发沿BD方向以1m/s匀速直线运动到D,若M,N同时出发,问出发后几秒钟时,△MON的面积为?
12.如图:已知正方形ABCD的边长为2cm,现在两动点P、Q分别从顶点B、A同时出发,当P沿线段BA以1cm/s的速度向点A运动,点Q沿折线A→D→C以2cm/s的速度向C运动.设点P、Q运动的时间为t(秒)
(1)当t为何值时,线段PQ与BC平行?
(2)设1≤t<2,当t为何值时,线段PQ将正方形ABCD的面积分为2:3两部分?
13.△ABC中,∠A=90°,∠C=30°,AB=1,两个动点P和Q同时从点A出发,P沿AC运动,Q沿AB,BC运动,结果两个动点同时到达点C.
(1)点Q的速度是点P速度的几倍?
(2)当AP为何值时,△APQ的面积为?
14.探究:如图.已知矩形OABC,顶点A、C分别在x、y 轴的正半轴上,点B的坐标为(8,4),M是BC的中点.动点P、Q同时从点O出发.分别沿线段OC和OA向点C和点A运动(任一点到达目的后两动点同时停止运动).点P的速度为1个单位/秒,点Q的速度为2个单位/秒.设运动的时间为t秒.求当t为何值时,△MPQ的面积为5平方单位?
15.如图,面积为50的等腰直角△ABC中,P为斜边上一动点,PQ⊥AC于Q,连接PC,求当动点P运动到恰好使△PCQ的面积为10时,△PCQ的周长.
16.如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,动点D从点A出发以4cm/s速度向点C移动,同时动点E从C出发以3cm/s的速度向点B移动,设它们的运动时间为ts.
(1)根据题意知:CE= ,CD= ;(用含t的代数式表示)
(2)t为何值时,△CDE的面积等于四边形ABED的面积的?
(3)点D、E运动时,DE的长可以是4cm吗?如果可以,请求出t的值,如果不可以,请说明理由.
17.如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A出发,以1cm/s的速度沿AB边向点B移动,以此同时,点Q从点C出发,以2cm/s的速度沿CB边向点B移动,如果P,Q同时出发,经过几秒,△PBQ的面积等于8cm2?
18.如图,在边长为12cm的等边三角形ABC中,点P从点A开始沿AB边向点B以每秒钟1cm的速度移动,点Q从点B开始沿BC边向点C以每秒钟2cm的速度移动.若P、Q分别从A、B同时出发,其中任意一点到达目的地后,两点同时停止运动,求:
(1)经过6秒后,BP= cm,BQ= cm;
(2)经过几秒后,△BPQ是直角三角形?
(3)经过几秒△BPQ的面积等于cm2?
19.如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?
(1)请你将小明对“思考题”的解答补充完整:
解:设点B将向外移动x米,即BB1=x,
则B1C=x+0.7,A1C=AC﹣AA1=﹣0.4=2
而A1B1=2.5,在Rt△A1B1C中,由B1C2+A1C2=A1B12得方程 ,
解方程得x1= ,x2= ,∴点B将向外移动 米.
(2)解完“思考题”后,小聪提出了如下问题:
梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?请你解答小聪提出的这个问题.
20.在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时点Q从点B沿边BC向点C以2cm/s的速度移动,设运动时间为t.
(1)问几秒后△PBQ的面积等于8cm2?
(2)是否存在t,使△PDQ的面积等于26cm2?
参考答案
1.解:(1)当运动时间为ts时,AP=3tcm,BP=(16﹣3t)cm,CQ=2tcm,DQ=(16﹣2t)cm.
故答案为:3tcm;(16﹣3t)cm;2tcm;(16﹣2t)cm.
(2)依题意得:[(16﹣3t)+2t]×6=33,
整理得:16﹣t=11,
解得:t=5.
答:当t为5时,四边形PBCQ的面积为33cm2.
(3)过点Q作QE⊥AB于点E,则PE=|(16﹣3t)﹣2t|=|16﹣5t|,如图所示.
依题意得:|16﹣5t|2+62=102,
即(16﹣5t)2=82,
解得:t1=,t2=.
答:当t为或时,点P和点Q的距离为10cm.
2.解:(1)由题意得:CP=AC﹣2t,CQ=t,
∴S=CP CQ=(AC﹣2t)t,
∵AC=12cm,BC=9cm,
∴S=(12﹣2t)t=﹣t2+6t;
(2)当S=5cm2时,
﹣t2+6t=5,
解得:t1=1,t2=5,
即当t=1或t=5时,Rt△CPQ的面积等于5cm2.
3.解:经过t秒后,PC=(4﹣2t)cm,CQ=tcm,
(1)若△CPQ为等腰三角形,
则PC=CQ,即4﹣2t=t,
解得:t=,
∴运动秒时,△CPQ为等腰三角形;
(2)当△CPQ的面积等于△ABC面积的时,
即×(4﹣2t) t=××3×4,
整理得:4t2﹣8t+3=0,
解得:t1=,t2=,
∴经过或秒后,△CPQ的面积等于△ABC面积的;
(3)∵∠C=90°,
∴(4﹣2t)2+t2=1,
整理得:5t2﹣16t+15=0,
∵Δ=162﹣4×5×15=256﹣300=﹣44<0,
∴此方程无实数解,
∴在运动过程中,PQ的长度不能为1cm.
4.解:如图1,当PB=PQ时,作PE⊥BC于E,
∴EQ=BQ,
∵CQ=t,
∴BQ=16﹣t,
∴EQ=8﹣t,
∴EC=8﹣t+t=8+t.
∴2t=8+t.
解得:t=.
如图2,当PQ=BQ时,作QE⊥AD于E,
∴∠PEQ=∠DEQ=90°,
∵∠C=∠D=90°,
∴∠C=∠D=∠DEQ=90°,
∴四边形DEQC是矩形,
∴DE=QC=t,
∴PE=t,QE=CD=12.
在Rt△PEQ中,由勾股定理,得
PQ=.
16﹣t=,
解得:t=;
如图3,当BP=BQ时,作PE⊥BC于E,
∵CQ=t,
∴BP=BQ=BC﹣CQ=16﹣t,
∵PD=2t,
∴CE=2t,
∴BE=16﹣2t,
在Rt△BEP中,
(16﹣2t)2+122=(16﹣t)2,
3t2﹣32t+144=0,
△=(﹣32)2﹣4×3×144=﹣704<0,
故方程无解.
综上所述,t=或时,以B,P,Q三点为顶点的三角形为等腰三角形.
5.解:(1)经过秒时,AP=cm,BQ=cm,
∵△ABC是边长为3cm的等边三角形,
∴AB=BC=3cm,∠B=60°,
∴BP=3﹣=cm,
∴△PBQ的面积=;
(2)设经过t秒△PBQ是直角三角形,
则AP=tcm,BQ=tcm,
△ABC中,AB=BC=3cm,∠B=60°,
∴BP=(3﹣t)cm,
△PBQ中,BP=(3﹣t)cm,BQ=tcm,若△PBQ是直角三角形,则∠BQP=90°或∠BPQ=90°,
当∠BQP=90°时,BQ=BP,
即t=(3﹣t),t=1(秒),
当∠BPQ=90°时,BP=BQ,
3﹣t=t,t=2(秒),
答:当t=1秒或t=2秒时,△PBQ是直角三角形.
(3)过P作PM⊥BC于M,
∴PM=(3﹣t),
∴S△PBQ=BQ PM= t (3﹣t),
∴y=S△ABC﹣S△PBQ=×32×﹣×t×(3﹣t)
=t2﹣t+,
∴y与t的关系式为y=t2﹣t+,
假设存在某一时刻t,使得四边形APQC的面积是△ABC面积的,
则S四边形APQC=S△ABC,
∴t2﹣t+=××32×,
∴t2﹣3t+3=0,
∵(﹣3)2﹣4×1×3<0,
∴方程无解,
∴无论t取何值,四边形APQC的面积都不可能是△ABC面积的.
6.解:(1)设经过ts,△AMN的面积等于矩形ABCD面积的,则DN=2tcm,AM=tcm,AN=AD﹣DN=(6﹣2t)cm,
∴AN AM=AD AB,即(6﹣2t)t=×6×3,
整理得:t2﹣3t+2=0,即(t﹣1)(t﹣2)=0,
解得:t1=1,t2=2,
则经过1s或2s,△AMN的面积等于矩形ABCD面积的;
(2)不存在,理由为:假设存在时间ts,使△AMN的面积达到3.5cm2,
则AN AM=3.5,
整理得:2t2﹣6t+7=0,
∵Δ=36﹣56=﹣20<0,
∴方程没有实数根,
则△AMN的面积不能达到3.5cm2.
7.解:(1)∵AP=t,CQ=2t,
∴t=3时,AP=3,CQ=6,
∴PC=6﹣3=3
在Rt△PCQ中,由勾股定理,得
PQ==3.
答:PQ=3;
(2)∵AP=t,CQ=2t,
∴PC=6﹣t.
∴(6﹣t)×2t=8,
解得:t1=2,t2=4.
(3)PQ、CD不互相平分.
当PQ、CD互相平分,
∴四边形PCQD是平行四边形,
∴PD∥CQ.PD=CQ.
∵点D为AB的中点,
∴P是AC的中点,
∴AP=AC=3,PD=CQ=BC=4.
∴t=≠.
∴PQ、CD不互相平分.
8.解:(1)由函数图象,得
OQ=2t,
故答案为:2t;
(2)当P在AO上,
,
解得:t1=2,t2=4.
∵t1=2,t2=4在0<t<6范围内,
∴t1=2,t2=4.
P在BO上,
=8,
解得:t3=3+,t4=3﹣.
∵t3=3+在6<t<12范围内,
∴t3=3+;
(3)在Rt△BOQ中,由勾股定理,得
BQ2=4t2+36,
BP=12﹣t,BP2=144﹣24t+t2,
∵△PBQ是等腰三角形,
∴PB=BQ,
∴PB2=BQ2,
∴4t2+36=144﹣24t+t2,
解得:t1=﹣4+2,t2=﹣4﹣2(舍去).
当PB=PQ时,BP2=144﹣24t+t2,PQ2=4t2+(6﹣t)2,
t1=,t2=(舍去).
故答案为:﹣4+2或.
9.解:(1)设经过t秒,△PBQ的面积等于8cm2则:
BP=6﹣t,BQ=2t,
所以S△PBQ=×(6﹣t)×2t=8,即t2﹣6t+8=0,
可得:t=2或4,即经过2秒或4秒,△PBQ的面积等于8cm2.
(2)根据(1)中所求出的S△PBQ=PB BQ=×(6﹣t)×2t,
整理得S△PBQ=﹣t2+6t(0<t<6).
则S五边形APQCD=S矩形ABCD﹣S△PBQ=72﹣(﹣t2+6t)=t2﹣6t+72=(t﹣3)2+63(0<t<6),
当t=﹣=3时,S五边形APQCD=63,
故当t=3秒,五边形APQCD的面积最小,最小值是63cm2,
(3)当t=1.5s时,
AP=1.5,BP=4.5,CQ=9,
∴DP2=146.25,PQ2=29.25,DQ2=117,
∴PQ2+DQ2=DP2,
∴△DPQ为Rt△;
(4)SDPBQ=6×12﹣t×12﹣×6(12﹣2t),
=72﹣36,
=36,
∴四边形DPBQ的面积是固定值36.
10.解:(1)过D点作DE⊥BC与E.
∵∠B=90°,
∴AB∥DE,
∵AD∥BC,
∴四边形ABED是矩形,
∴AD=BE,AB=DE,
∵∠C=45°,
∴EC=DE=4cm,
∴AD=BE=BC﹣EC=5cm;
(2)当t=2时,BP=2cm,BQ=9﹣2=7cm,
△PBQ的面积=2×7÷2=7cm2;
(3)P点在AB上时,t(9﹣t)÷2=9,解得t1=3,t2=6(不合题意舍去);
P点在AD上,4(9﹣t)÷2=9,解得t=4.5.
故t=3或4.5时,y的值是9cm2.
故答案为:5cm.
11.解:设出发后x秒时,
(1)当x<2时,点M在线段AO上,点N在线段BO上.(4﹣2x)(3﹣x)=;
解得x1=,x2=
∵x<2,
∴;
(2)当2<x<3时,点M在线段OC上,点N在线段BO上,(2x﹣4)(3﹣x)=;
解得;
(3)当3<x≤4时,点M在线段OC上,点N在线段OD上,(2x﹣4)(x﹣3)=;
解得x1=s或x2=s.
综上所述,出发后或s或时,△MON的面积为.
12.解:由题意,得
2t﹣2=2﹣t,
解得:t=.
答:t=s时,线段PQ与BC平行;
(2)∵正方形的边长为2cm,
∴正方形的面积为:4cm2.
∴PQ分得的两部分的面积分别为:cm2,cm2.
如图1,当S△PAQ=时,
(2﹣t)2t×=,
5t2﹣10t+8=0,Δ<0,此方程无解.
如图2,当四边形APQD=时,
=,
解得:t=.
如图2,当四边形APQD=时,
=,
解得:t=>2(舍去).
∴当t=时,线段PQ将正方形ABCD的面积分为2:3两部分.
13.解:(1)∵在△ABC中,∠A=90°,∠C=30°,AB=1,
∴BC=2,AC=,
∵两个动点P,Q同时从A点出发,点P沿AC运动,点Q沿AB,BC运动,两点同时到达点C
∴Q的速度是P的速度的(2+1)÷=倍;
(2)设AP=x,由(1)知Q点运动路程为x,
①点Q在AB上运动,0≤≤1,即0≤x≤,
当点Q与点B重合时,△APQ的面积最大;
此时AQ=AB=1,则AP=,
故△APQ的面积为:=<;
②点Q在BC上运动,1<≤3,即<x≤;
如图所示,过点Q作QM⊥AC,垂足为M,
则CQ=3﹣x,
∵在△ABC中,∠A=90°,∠C=30°,
∴QM=CQ=,
根据题意,得:,
解得:x=(符合题意).
答:当AP为时,△APQ的面积为.
14.解:设t秒时,△MPQ的面积为5平方单位,
由题意可得:PC=4﹣t,PO=t,QO=2t,AQ=8﹣2t,BM=CM=4,AB=4,
故S△PMQ=S矩形ABCO﹣S△OPQ﹣S△PCM﹣S梯形AQBM
5=4×8﹣t 2t﹣(4﹣t) 4﹣(4+8﹣2t)×4
整理得:t2﹣6t+5=0,
解得:t1=1,t2=5(不合题意舍去),
答:当t为1秒时,△MPQ的面积为5平方单位.
15.解:设AC=x,则BC=x.
∵等腰直角△ABC的面积为50,
∴x2=50,
解得x=±10(负值舍去),
∴AC=BC=10.
设PQ=y,则AQ=y,CQ=10﹣y.
∵△PCQ的面积为10,
∴y(10﹣y)=10,
解得y=5±,
当y=5+时,PQ=5+,CQ=5﹣,PC==2;
当y=5﹣时,PQ=5﹣,CQ=5+,PC==2;
∴△PCQ的周长=PQ+CQ+PC=10+PC=10+2.
16.解:(1)∵动点D、E同时出发,动点E从C出发向点B移动,
∴CE=3tcm,
∵动点D从点A出发向点C移动,
∴CD=(8﹣4t)cm,
故答案为:3tcm,(8﹣4t)cm.
(2)当△CDE的面积等于四边形ABED的面积的时,则△CDE的面积等于△ABC的面积的,
根据题意得×3t(8﹣4t)=××8×6,
整理得t2﹣2t+1=0,
解得t1=t2=1,
答:t=1,即运动1秒时,△CDE的面积等于四边形ABED的面积的.
(3)不可以,理由如下:
如果可以,则由勾股定理得(3t)2+(8﹣4t)2=42,
整理得25t2﹣64t+48=0,
∵Δ=(﹣64)2﹣4×25×48=﹣704<0,
∴该方程没有实数根,
∴DE的长不可以是4cm.
17.解:设xs后,可使△PBQ的面积为8cm2.
由题意得,AP=xcm,PB=(6﹣x)cm,BQ=(8﹣2x)cm,
则(6﹣x) (8﹣2x)=8,
整理,得x2﹣10x+16=0,
解得x1=2,x2=8(不合题意舍去).
所以P、Q同时出发,2s后可使△PBQ的面积为8cm2.
18.解:(1)由题意,得
AP=6cm,BQ=12cm.
∵△ABC是等边三角形,
∴AB=BC=12cm,
∴BP=12﹣6=6cm.
故答案为:6、12.
(2)∵△ABC是等边三角形,
∴AB=BC=12cm,∠A=∠B=∠C=60°,
当∠PQB=90°时,
∴∠BPQ=30°,
∴BP=2BQ.
∵BP=12﹣x,BQ=2x,
∴12﹣x=2×2x,
∴x=,
当∠QPB=90°时,
∴∠PQB=30°,
∴BQ=2PB,
∴2x=2(12﹣x),
x=6
答6秒或秒时,△BPQ是直角三角形;
(3)作QD⊥AB于D,
∴∠QDB=90°,
∴∠DQB=30°,
∴DB=BQ=x,
在Rt△DBQ中,由勾股定理,得
DQ=x,
∴,
解得;x1=10,x2=2,
∵x=10时,2x>12,故舍去
∴x=2.
答:经过2秒△BPQ的面积等于cm2.
19.解:(1)设点B将向外移动x米,即BB1=x,
则B1C=x+0.7,A1C=AC﹣AA1=﹣0.4=2.
而A1B1=2.5,在Rt△A1B1C中,由B1C2+A1C2=A1B12得方程(x+0.7)2+22=2.52,
解方程得x1=0.8,x2=﹣2.2(不合题意舍去),∴点B将向外移动0.8m.
故答案为(x+0.7)2+22=2.52,0.8,﹣2.2(不合题意舍去),0.8;
(2)有可能.
设梯子顶端从A处下滑x米,点B向外也移动x米,
则有(x+0.7)2+(2.4﹣x)2=2.52,
解得:x1=1.7或x2=0(不合题意舍去).
故当梯子顶端从A处下滑1.7米时,点B向外也移动1.7米,即梯子顶端从A处沿墙AC下滑的距离与点B向外移动的距离有可能相等.
20.解:(1)设x秒后△PBQ的面积等于8cm2,
∵AP=x,QB=2x.
∴PB=6﹣x.
∴×(6﹣x)2x=8,
解得x1=2,x2=4,
答:2秒或4秒后△PBQ的面积等于8cm2;
(2)假设存在t使得△PDQ面积为26cm2,
则72﹣6t﹣t(6﹣t)﹣3(12﹣2t)=26,
整理得,t2﹣6t+10=0,
∵△=36﹣4×1×10=﹣4<0,
∴原方程无解,
所以不存在t,能够使△PDQ的面积等于26cm2.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
