7.1常量和变量

课件31张PPT。7.1 常量与变量我国海监船以40千米/时的速度从温州港出发前去钓鱼岛进行日常巡视。设海监船行驶时
20408012040t 会变化的量是：
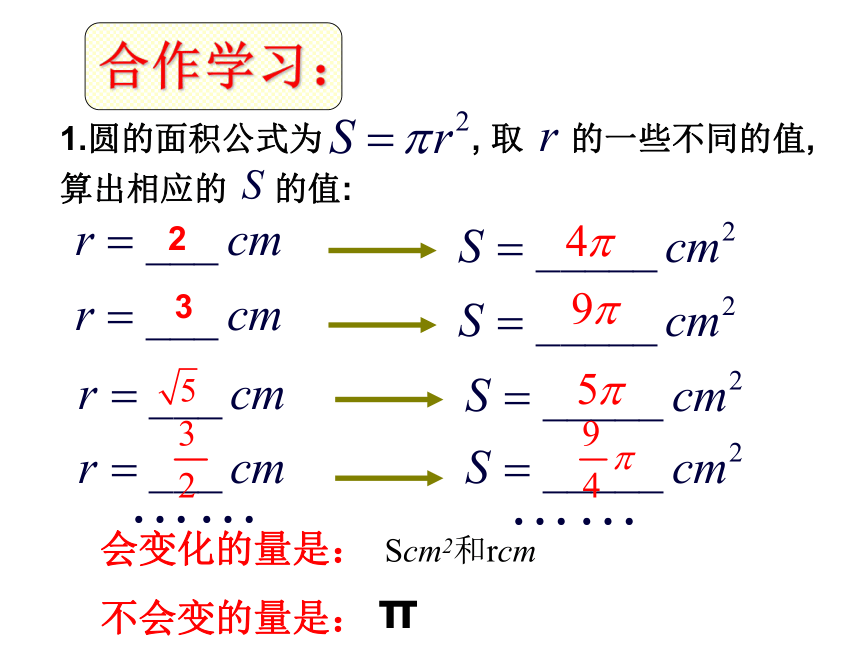
不会变的量是： t时和s千米40千米/时40t间为t时，行驶路程为s千米。则s＝　 。合作学习：32会变化的量是：
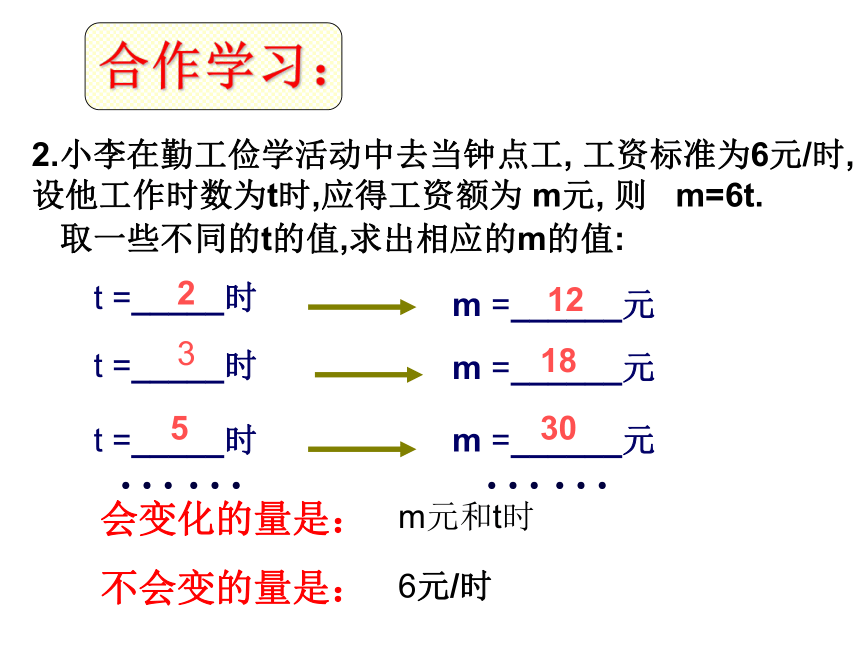
不会变的量是：Scm2和rcmπ2.小李在勤工俭学活动中去当钟点工, 工资标准为6元/时,设他工作时数为t时,应得工资额为 m元, 则 m=6t.t =_____时m =______元m =______元m =______元t =_____时t =_____时取一些不同的t的值,求出相应的m的值:305321812会变化的量是：
不会变的量是：m元和t时6元/时合作学习：概念1.在一个过程中,固定不变的量称为常量.2.在一个过程中,可以取不同数值的量称为变量. m=6tS=40t指出下列事件中的常量与变量1.长方形的长和宽分别是a与b，周长Ｃ＝２（a＋ b ），其中常量是　　，变量是　　　　　。２.圆锥体积v与圆锥底面半径r圆锥高h之间存在关系式v＝（１／３）πr２h，其中常量是　　　　 ，变量是　　　　　　。 ３.某种报纸每份a元，购买x份此种报纸共需y元，则 y＝ax中的常量是　　　　，变量是　　　　　　。２C,a,bv,r,hay,x4、声音在空气中传播的速度v(m/s)与温度t(oC)
之间的关系式是v=331+0.6t，其中常量是______，变量是_____。
331,0.6v，t练一练议一议:（1）汽车以50千米/时的速度行驶，用t时表示行驶的时间，s千米表示行驶路程，其中常量是 ，变量是 . 50千米/时t时， s千米sV，t结论：常量和变量是对某一变化过程来说，不是绝对的是相对的.常量不一定是具体的数，也有用字母表示的.若V一定呢？（2）在行程问题中，s=vt，s一定时，常量是 ，变量是 .钓鱼岛主岛距温州市约360千米，视频神六飞天，成功着陆。例：先看下面报道：
2005年10月17日凌晨4时33分 ，神舟六号返回舱在内蒙古四子王旗成功着陆，航天员费俊龙、聂海胜平安返回 。在着陆前的最后48分时间内，它是在耐高温表层的保护下，以7800米／秒的速度冲入100千米厚的地球大气层。在空气阻力的作用下，它在距地球表面10千米左右时，以180米／秒的速度下降 ，此时直径20多米的降落伞自动打开。“神舟六号”着陆前的最后48分时间内，
飞船运动的时间、 飞船运动的速度、
飞船所受地球的引力，
飞船着陆前48分那时的位置到着陆点的距离。请问：下面哪些是常量？哪些是变量？ 指出下列事件过程中的常量与变量
　⒈某水果店橘子的单价为２.５元／千克，买Ｋ千克橘子的总价为Ｓ元，其中常量是
——————，变量是——————。
　⒉　圆周长Ｃ与圆的半径r之间的关系式是Ｃ＝２πr，其中常量是——————，
变量是—————— 。
。２.５Ｋ，Ｓ２，πＣ， r小组合作请每个同学举一个常量和变量的实际例子。这节课你有什么收获？作业：必做题：1、书上作业题A组
2、作业本
选做题：书上作业题B组
请你试试：通过报刊、互联网等途径查
找资料，写一段涉及较多量
的短文，找出其中的变量和
常量，并说明你的理由。问题1 火车以60千米/时的速度匀速行驶，行驶的路程为S千米,行驶的时间为t小时.
60120180240300S=60t常量是什么? 变量是什么? 每张电影票的售价为10元,如果早场售出票150张,日场售出票205张,晚场售出票310张,三场电影的票房收入各多少元?
问题2 设一场电影售出票x张,票房收入为y元,怎样用含x的式子表示y?
y=10x常量是什么? 变量是什么?.在一根弹簧的下端悬挂重物，改变并记录重物的质量，观察并记录弹簧长度的变化，探索它们的变化规律。如果弹簧原长10cm，每1kg的重物使弹簧伸长0.5cm，怎样用含有重物质量m的的式子表示受力后弹簧的长度l？ 挂1kg重物时弹簧的长度：1×0.5+10=10.5（cm）挂2kg重物时弹簧的长度：2×0.5+10=11（cm）挂3kg重物时弹簧的长度：3×0.5+10=11.5（cm） l =0.5m+10 问题3常量是什么? 变量是什么?问题4 要画一个面积为10 的圆，圆的半径应取多少？圆面积为20 呢？怎样用含圆面积S的式子表示圆半径r？r=常量是什么? 变量是什么?问题5 用10m长的绳子围成长方形。试改变长方形的长度，观察长方形的面积怎样变化。记录不同的长方形的长度值，计算相应的长方形面积的值，探索它们的变化规律。设长方形的长为xm，面积为S ，怎样用含x的式子表示S？S=x(5-x)14262.56.2536常量是什么? 变量是什么?浏阳市出租车起步价为3元，2公里以后
每公里收费为1.2元，如果出租车行驶里程为
x千米（x≥2），乘客所付车费为y元，则怎
样用含有行驶里程数x的代数式表示乘客所付
车费y？y=1.2x+0.6(x ≥2)问题6练习：
分别指出下列各关系式中的变量与常量：（1）圆的面积公式
（2）正多边形的 内角公式
（a是正多边形一个内角的度数，n为正多边形的边数）
（3）匀速运动公式
（t表示时间，v表示速度,s表示在t时间内所走的路程）变量是r和S变量是α和n变量是t和S常量是2和180°常量是v　　受日月的引力而产生潮汐现象，早晨海水上涨叫做潮，黄昏海水上涨叫做汐，合称潮汐．潮汐与人类的生活有着密切的联系．某港口从０时到１２时的水深情况如下表，其中t表示时刻，h表示水深．在上述问题中，字母t，h表示的是变量还是常量？简述你的理由．解： t，h表示的是变量，因为在０时到１２时这一时刻， t的值在变化，h的值也相应着变化.观察下列直棱柱，回答问题 １.直三棱柱有几个面？
　　直四棱柱有几个面？　
直五棱柱有几个面？
２.直n棱柱有几个面？若用m表示直n棱柱的面数，试写出m与n之间的关系式；３.指出你所写的关系式中，哪些是常量？　　　哪些是变量？５个面６个面
７个面
解： 直n棱柱有（n＋２）个面
关系式是： m＝n＋２m，n２2、如图,在ΔABC中,点E是高线AD上的一个动点,连结BE、CE,点E 在AD上移动的过程中, 哪些量是常量?哪些量是变量?拓展提高你能预测自己将来的身高吗?若a，b分别表示父母的身高,h男，h女分别表示儿女成人时的身高，则有关系式： h男＝０.５４（a+b ）
　　h女＝（０.９７５a+b）÷２你们能预测出全班同学成人时的身高吗？这里什么是常量？什么是变量？小组合作，挑战他组１.　举2个常量和变量的实际例子 ２.　确定出要挑战的小组3. 出题组提问,被挑战组答出常量与变量(一人答一题)练习:
1.购买一些钢笔,单价2元/支,总价y元随钢笔支数x变化,指出其中的常量与变量,并写出关系式.
2.一个三角形的底边长5cm,高h可以任意伸缩,写出面积S随h变化关系式,并指出其中常量与变量.
3.每张电影票的售价为10元,如果早场售出票150张,日场售出票205张,晚场售出票310张,三场电影收入各多少元?
设一场电影票出售x张,票房收入为y元,怎样用含x的式子表示y?
4.在一根弹簧的下端悬挂重物,改变并记录重物的质量,观察并记录弹簧长度的变化,探索它们的变化规律.如果弹簧原长10cm,每1kg重物使弹簧伸长0.5cm,怎样用含重物质量m(单位:kg)的式子表示受力后的弹簧长度(单位:cm).5.要画一个面积为10cm2的圆,圆的半径应取多少?圆面积为20cm2呢?怎样用含圆面积s的式子表示圆半径r?
6.如图:用10m长的绳子围成长方形,试改变长方形的长度,观察长方形的面积怎样变化.记录不同的长方形的长度值,计算相应的长方形面积的值,探索它们的变化规律.设长方形的长为xm,面积为Sm2,怎样用含x的式子表示S?瓶子或罐头盒等物体如图那样堆放.试确定瓶子总数y与层数x之间的关系式.随堂练习2：VR2.汽车开始行使时油箱内有油40升，如果每小时耗油5升，则油箱内余油量Q升与行使时间t小时的关系是 . 并指出其中的常量与变量？ Q=40-5t3.夏季高山上温度从山脚起每升高100米降低0.7°C,已知山脚下温度是23°C,则温度y与上升高度x之间关系式为______________.再见！