5.1 多边形(1)

课件20张PPT。只凭风力健，
不加羽毛丰。
红线凌空去，
清云有路通。
　猜谜语猜一活动名称　　周末老师去商店看到了几个风筝，请你说说它们类似于哪些几何图形?5.1 多边形（1）

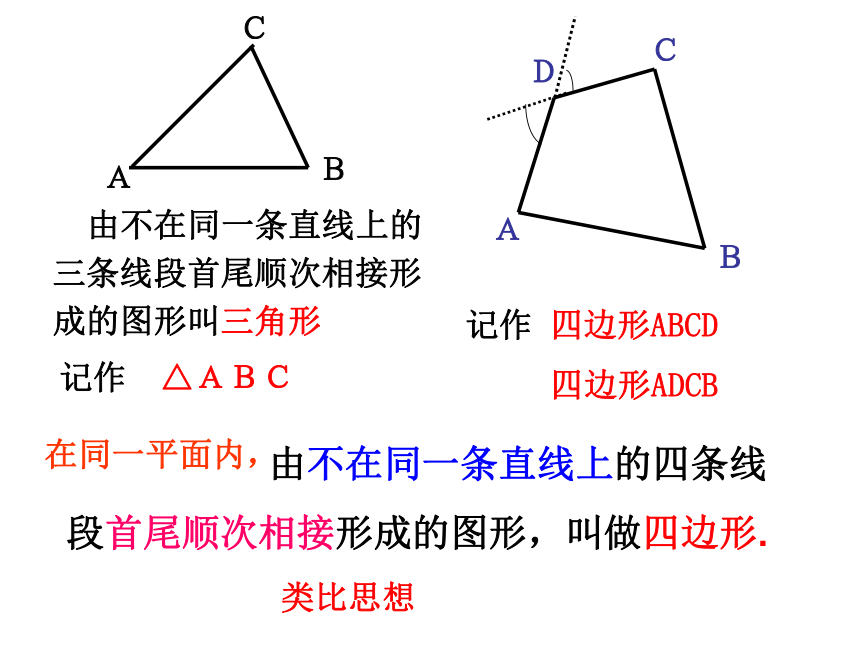
—— 四边形ＡＣＢＤＡＢＣ记作 △ＡＢＣ记作 四边形ABCD
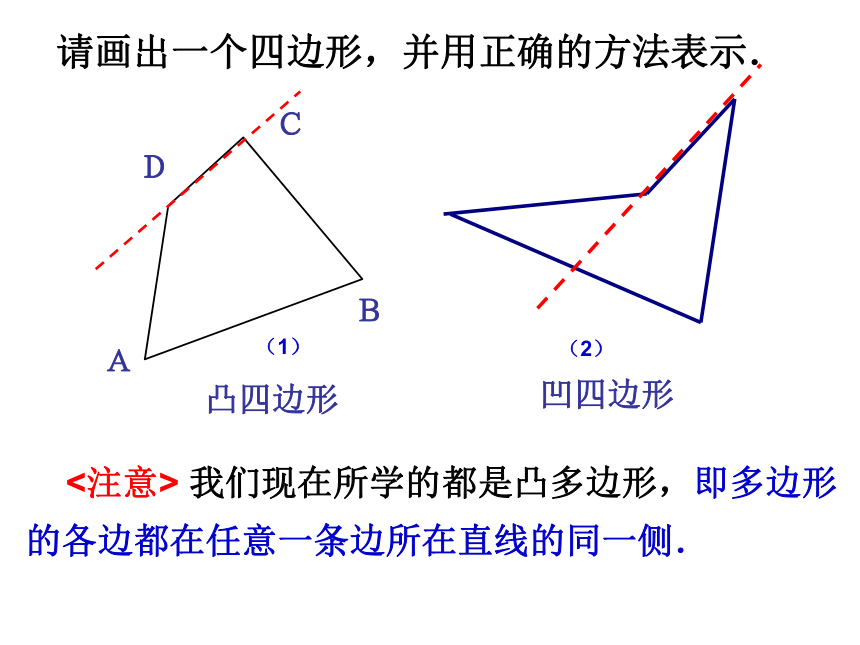
四边形ADCB 由不在同一条直线上的三条线段首尾顺次相接形成的图形叫三角形 由不在同一条直线上的四条线段首尾顺次相接形成的图形，叫做四边形.在同一平面内，类比思想凸四边形凹四边形 <注意> 我们现在所学的都是凸多边形，即多边形
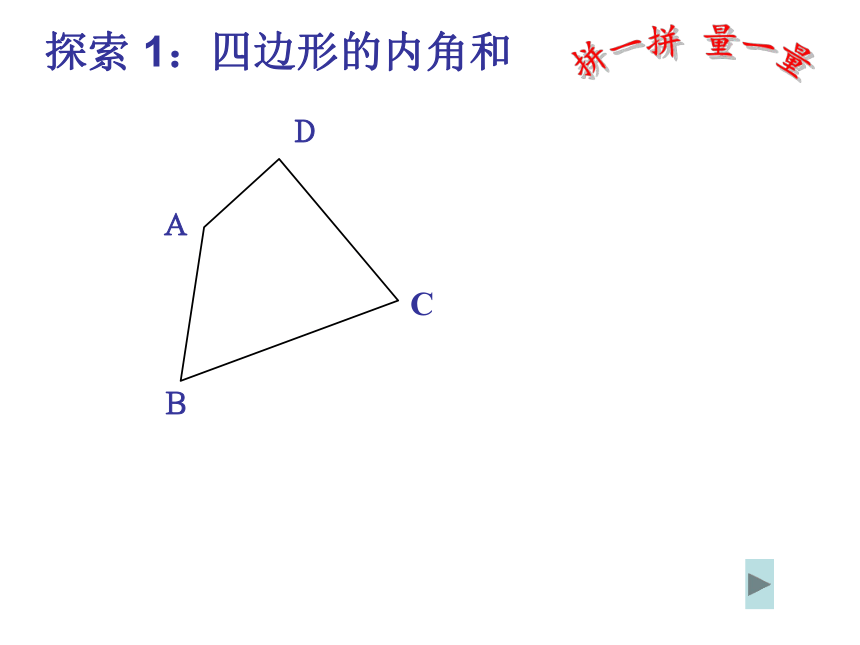
的各边都在任意一条边所在直线的同一侧．请画出一个四边形，并用正确的方法表示．（1）（2）ＡＣＢＤ生 活 中 的 四 边 形探索 1：四边形的内角和拼一拼 量一量ＡＢＤC 猜想：四边形的内角和等于360° 符号表示：四边形ABCD中
∠ A＋ ∠A BC＋ ∠C ＋ ∠ADC＝ 360°
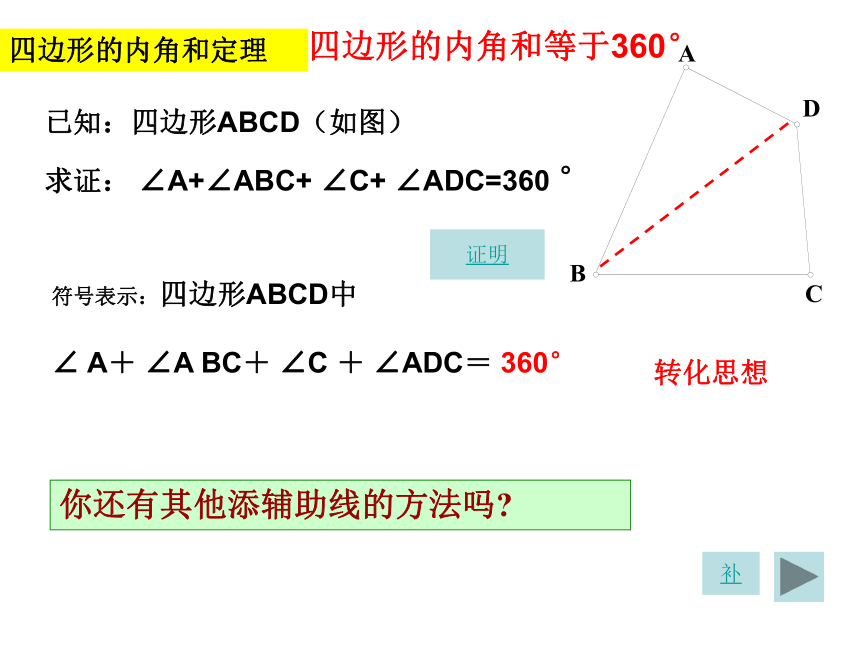
已知：四边形ABCD（如图）
求证： ∠A+∠ABC+ ∠C+ ∠ADC=360 °转化思想你还有其他添辅助线的方法吗?四边形的内角和定理证明补已知：四边形ABCD（如图）
求证： ∠A+∠B+ ∠C+ ∠D=360 °证明：连结BD ∵ ∠ABD+∠A+ ∠ADB =180 °
∠DBC+∠C+ ∠CDB =180 °
(三角形三个内角的和等于180 °)∴ ∠ABD+∠A+ ∠ADB + ∠DBC+∠C+ ∠CDB
=180 °+ 180° = 360°即∠A+∠ABC+∠C+∠ADC=360 °EF12341个三角形内角和 + 1个平角ABCDABCDABCD“割”“补”“平行” 转化思想小结已知四边形ABCD中，
∠B＝80 °, ∠A＝85°, ∠C=75°
则∠D=_____. 做一做∠A与∠C互补_________________ 例1、如图，四边形风筝的四个内角∠A、∠B、∠C、∠D的度数之比为1∶1∶0.6∶1，求它的四个内角的度数．解：设∠A为x度，由题意可得：∠B，∠C，∠D分别为x，0.6x，x∵∠A+∠B+∠C+∠D=3600（四边形的内角和为3600）∴x+x+0.6x+x=360解得，x=100∴∠A=∠B=∠D=1000，∠C=600方程思想EABC2134 解 :∵∠ 1+∠5 =∠2+ ∠6= ∠3+∠7
= ∠ 4+∠8= 180°
∴ ∠ 1+∠5 +∠2+ ∠6 + ∠3+∠7+ ∠ 4+∠8
= 4× 180°= 720°
∵ ∠5 +∠ 6 + ∠ 7 +∠8=360°(四边形的内角和是360°)
∴ ∠1 +∠ 2 + ∠ 3 +∠4 = 720°－ 360°= 360°
四边形的外角和等于360度。即:∠ 1＋∠ 2+ ∠3 +∠4 = 360°5678猜想：探索 2：四边形的外角和推论：四边形的外角和等于3600体 验 成 功４３思考：四边形的内角最多有_____个直角？最多有_____个钝角？
1、如图：求∠D的度数。 10009501100你知道怎样用一批大小，形状一样的四边形木板，
密铺成一块面积更大的地板吗？生活大探秘(密铺:即镶嵌,用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙,不重叠的铺成一片。 )（２）每跑完一圈，身体转过的角度之和是多少？∠1，∠2，∠3，∠4∠1+∠2+∠3+∠4 = ？ 拿着风筝沿着一个四边形广场周围的小路，按逆时针方向跑了一圈． （１）每从一条小路转到下一条小路时，身体转过的角是哪个角？5放风筝啰！四边形的外角和等于360°(3)广场周围有四个圆形花坛，四边形的四个顶点恰好都在圆心上。若圆的半径为2，你能计算花坛阴影部分的总面积吗？（结果保留∏）一个定义，一个定理，一个推论 2. 重要数学思想方法三角形的概念 四边形的概念
转化类比反思与小结四边形问题三角形问题猜想证明
②你能否发现并找出五边形,六边形的内角和与外角和的规律吗?
作业布置必做题
⑴作业题(A组)③生活中,四边形可以用来密铺平面,其它多边形可以吗?密铺的数学原理是什么?①你还能找到其他得到四边形内角和定理的方法吗？思考题风 筝 因 为 风 儿 而 飞 翔人 类 因 为 思考 而 飞 翔让 我 们 一 起 想 象，
让 我 们 一 起 飞 翔！谢谢大家