5.1(2)多边形

课件25张PPT。由上述这些图形，你能
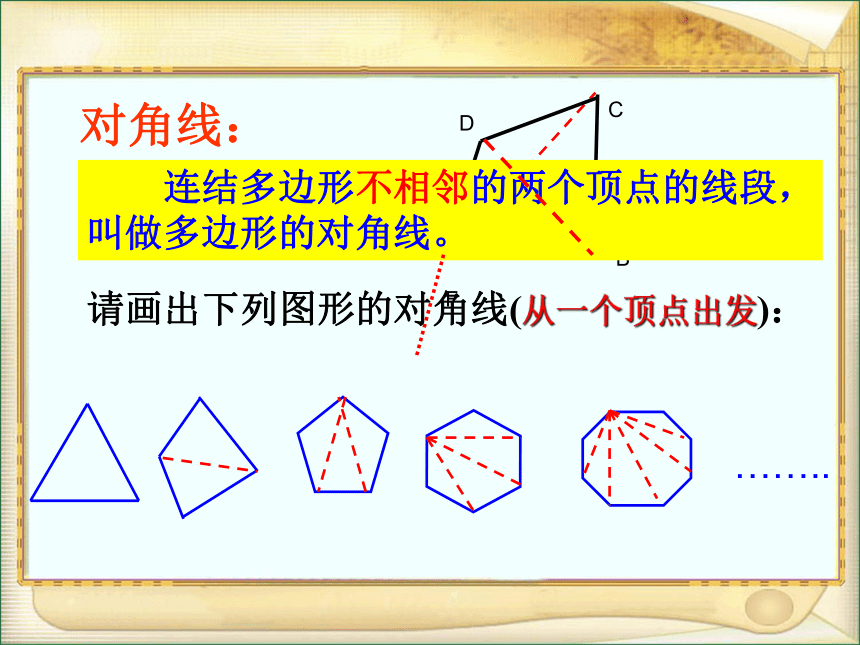
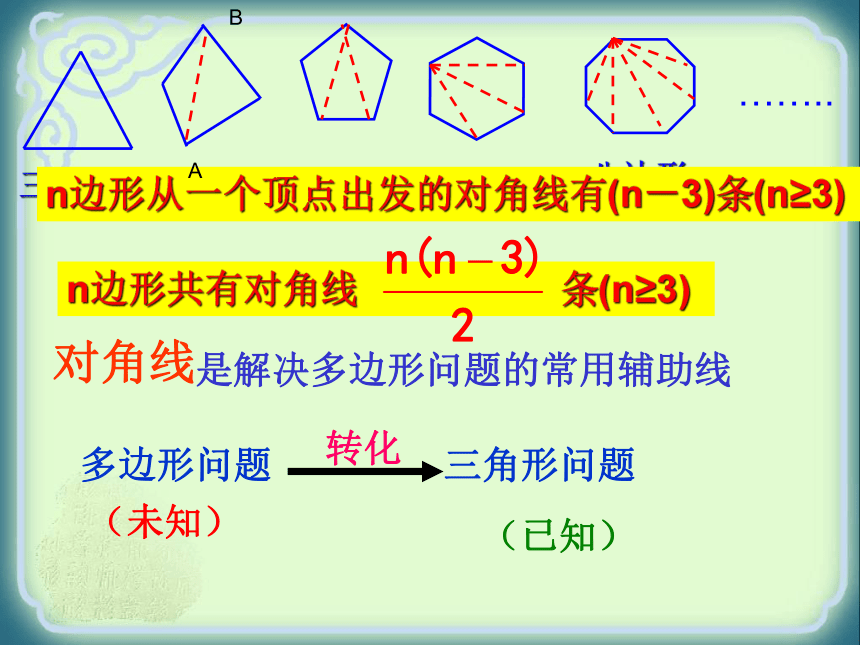
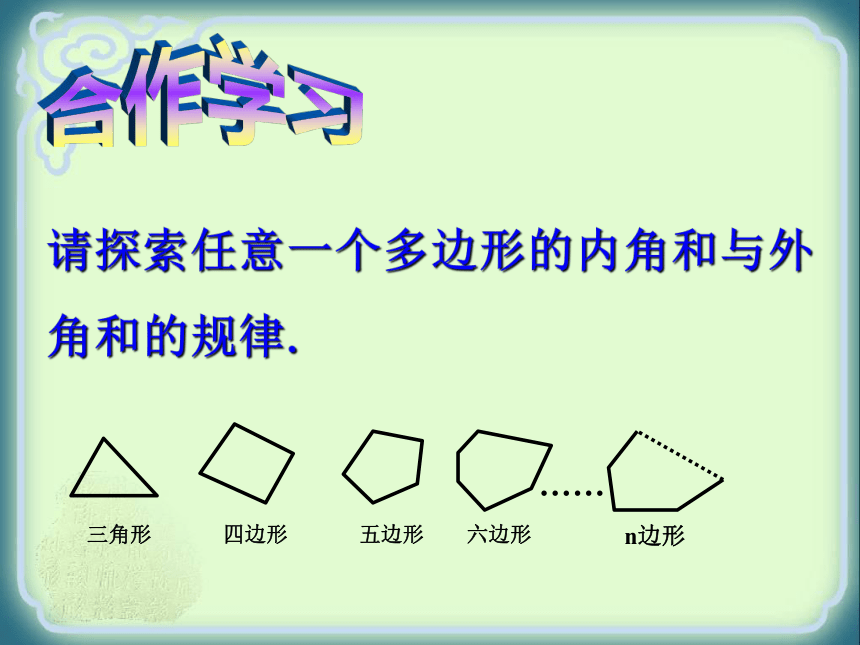
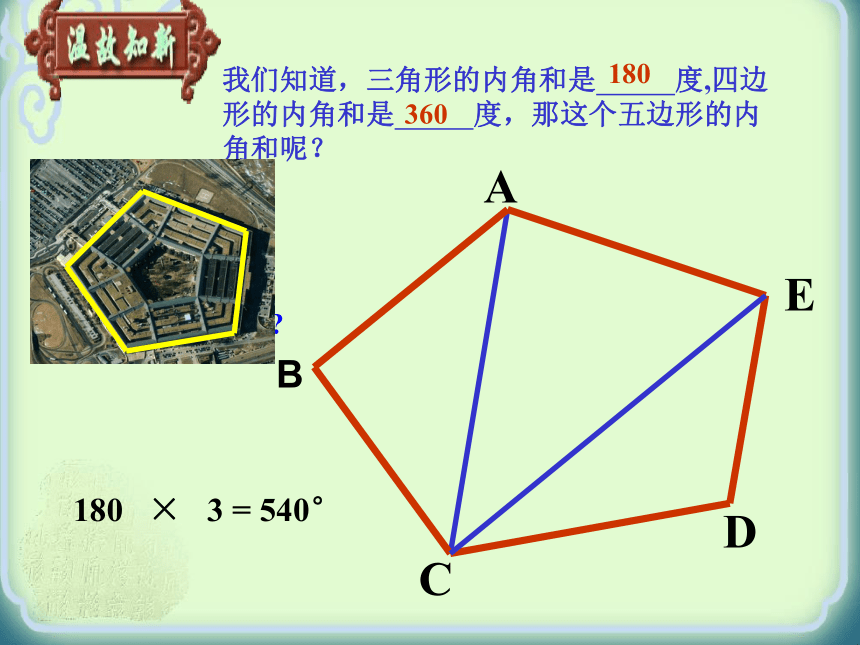
抽象出什么几何图形？三角形 四边形 六边形 八边形……..五边形三角形的定义：　　在同一平面内，由不在同一条直线上的三条线段首尾顺次相接所组成的图形。多边形的定义：　　在同一平面内，由不在同一条直线上的一些线段首尾顺次相接所组成的（封闭）图形。……五边形六边形七边形类似地，边数为n的多边形叫做n边形（n为大于或等于３的正整数）．－探索多边形的内角和、外角和多边形（2）对角线：　　连结多边形不相邻的两个顶点的线段，叫做多边形的对角线。请画出下列图形的对角线(从一个顶点出发)：……..三角形六边形四边形八边形……..五边形是解决多边形问题的常用辅助线 对角线多边形问题 三角形问题转化（未知）（已知）n边形从一个顶点出发的对角线有(n－3)条(n≥3)n边形共有对角线 条(n≥3)AB合作学习请探索任意一个多边形的内角和与外角和的规律.我们知道，三角形的内角和是 度,四边形的内角和是 度，那这个五边形的内角和呢？180360你能动手做一做吗?DECB A180 × 3 = 540°E
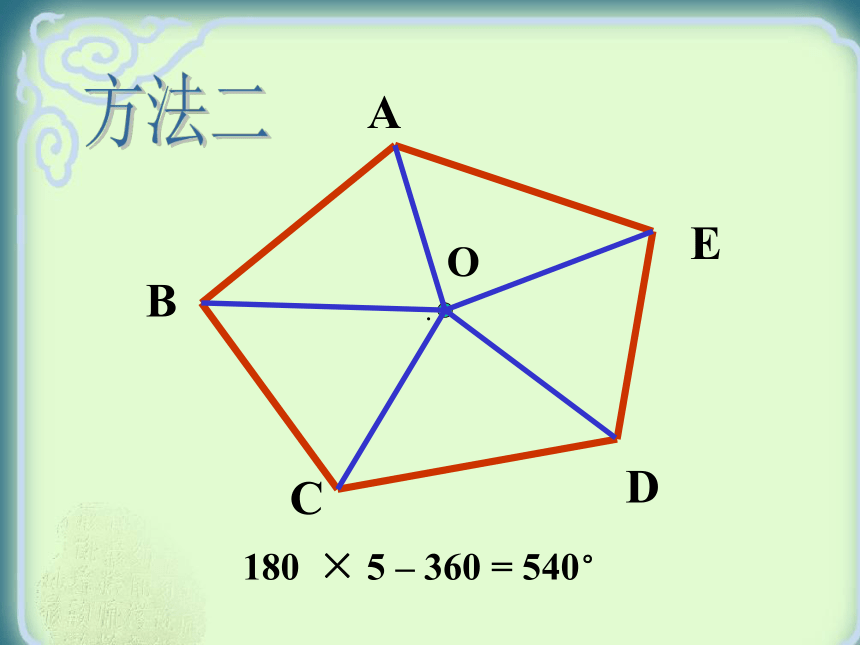
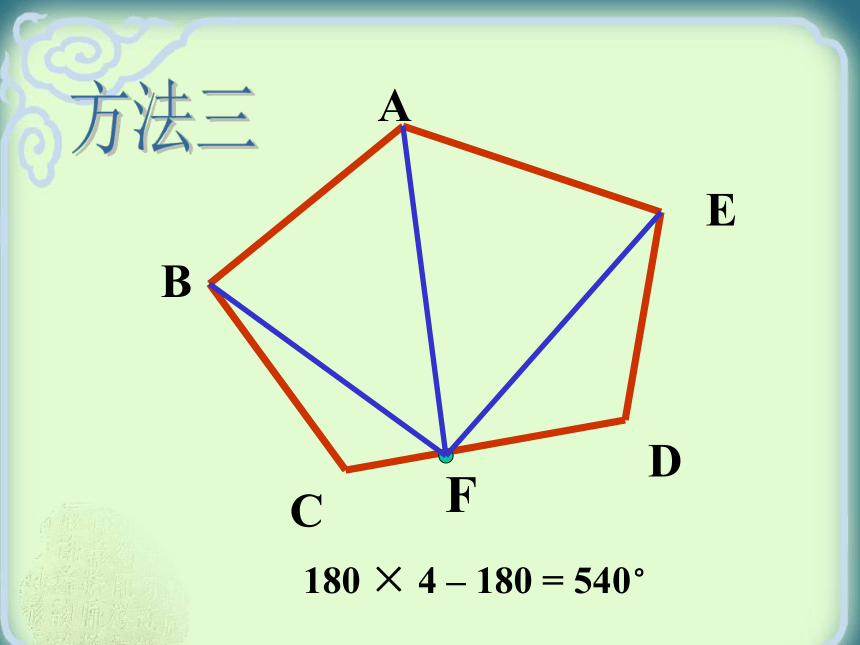
BCD.O A180 × 5 – 360 = 540°方法二BCDEF180 × 4 – 180 = 540°A方法三180×4－180=540°BCDEFA方法四合作交流，探究新知 ：仔细思考，并请填写下表：23343×180°4×180°n－ 3n－ 2（n－2）×180° 数学学习者小数学天才小小数学家荣誉级别晋升规则：
从低级到高级逐步提高数学爱好者3×180o-1×180o=360o4×180o-2×180o=360o5×180o-3×180o=360o6×180o-4×180o=360on×180o-(n-2)×180o=360o合作学习多边形的外角和ABCn边形的内角和为（n-2）X 180o （n≥3)任何多边形的外角和为360o结论：数学学习者小数学天才小小数学家荣誉级别晋升规则：
从低级到高级逐步提高数学爱好者（2）已知一个多边形的内角和为900o ，则这个多边形是______边形七（1）八边形的内角和为______.1080数学学习者已知一个多边形的每一个外角都是72o，求这个边形的边数为______数学爱好者5例1、一个六边形如图，已知AB∥DE，BC∥EF，CD∥AF，求∠A＋∠C＋∠E的度数。 ∵AB∥DE， CD∥AF（已知）∴∠1＝∠3，∠2＝∠4
（两直线平行，内错角相等） ∴∠1+∠2＝∠3+∠4，
即∠FAB＝∠CDE，同理∠B＝∠E，∠C＝∠F∴∠FAB＋∠C＋∠E= 1／2 ×720°=360°思考：有没有其它的解法？∵∠FAB+∠ABC+∠BCD+∠CDE＋∠DEF＋∠AFE=（6-2）×180°=720°如图所示：可向两个方向分别延长AB，CD，EF三条边，构成△PQR。∵ DE∥AB
∴∠1=∠R,同理∠2=∠R
∴∠1＝∠2，∴∠CDE=∠FAB同理∠AFE＝∠BCD，∠ABC=∠DEF∴∠FAB＋∠BCD＋∠DEF= 1／2 ×720°=360°解法二：一个六边形如图，已知 BA∥DE ，∠B= ∠ E，∠C=∠F
（1）求证：CD∥AF
（2）求∠A＋∠C＋∠E的度数．小小数学家已知
;
;六边形ABCDEF的每个内角度数是120度,且AF=AB=3,BC=CD=2.
求：DE，EF的长度．小小数学家B1B2B3B4B5A1A2A3A4A5 一个五角星图案如图,已知五边形A1A2A3A4A5的各个内角都相等,分别求∠B1,∠B2,∠B3,∠B4,∠B5,的度数.自我挑战这节课你学到了什么?
还有什么困惑？1.定义、结论2. 一种重要数学思想方法（转化思想）小结:是解决多边形问题的常用辅助线 对角线多边形问题 三角形问题转化（未知）（已知）n边形的内角和为(n－2) ×180°(n≥3)n边形从一个顶点出发的对角线有(n－3)条(n≥3)n边形共有对角线 条(n≥3)任何多边形的外角和为360°结论下课了，再见！