2.1一元二次方程（1）

课件13张PPT。问题1:老师昨天和朋友一起去买了些贺卡，我们共买了23张贺卡，她比我少买一张，你们知道老师买了几张贺卡？设老师买了x张贺卡,可列出方程: 问题2:若要做一张面积为900平方厘米的长方形贺卡，并且长比宽多10厘米，则贺卡的长和宽各为多少厘米？ 设贺卡的长为x厘米,可列出方程： 问题3:若把面积为4平方分米的一张纸分割成如图所示的正方形和长方形两个部分做贺卡，求正方形的边长。 设正方形的边长为y分米，可列出方程: yx+x-1=23尝试归纳得到
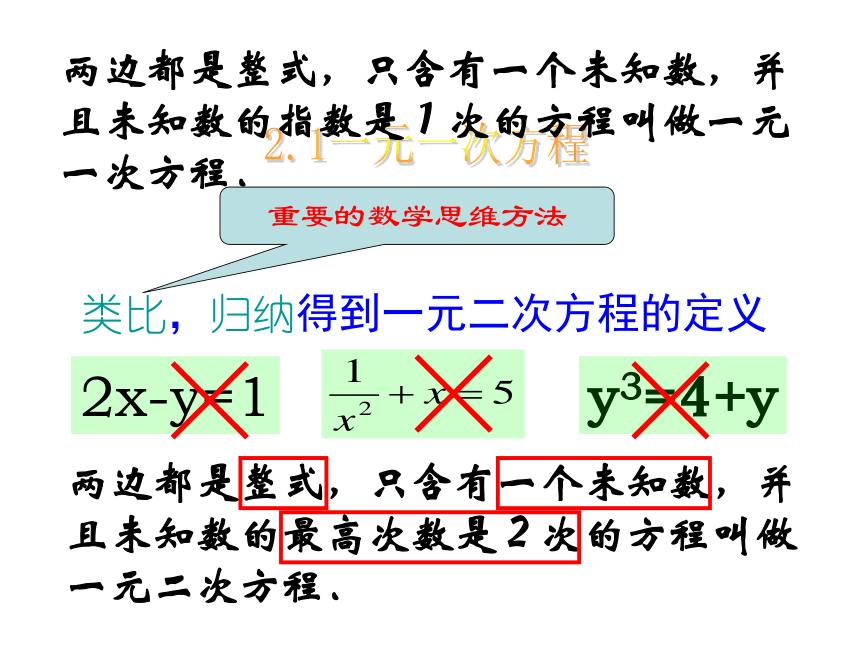
一元二次方程定义一元一次方程 观察上述两个方程与一元一次方程有什么相同点和不同点类比方程两边都是整式
只含有一个未知数
未知数的指数是１次相同点：不同点：未知数的最高次数是2次方程两边都是整式只含有一个未知数①x+x-1=23②③类比，归纳得到一元二次方程的定义两边都是整式，只含有一个未知数，并且未知数的最高次数是２次的方程叫做一元二次方程．重要的数学思维方法2x-y=1y3=4+y2.1一元一次方程两边都是整式，只含有一个未知数，并且未知数的指数是１次的方程叫做一元一次方程．判断下列方程是否为一元二次方程：① 4x2=5 ( ) ②2(x-1)=3x ( )
③2x2-3y-1=0 ( ) ④ ( )
⑤9x2=5-4x ( ) ⑥ ( )
⑦ 2a+7b=0 ( ) ⑧(2-x)(3x+4)=3 ( )
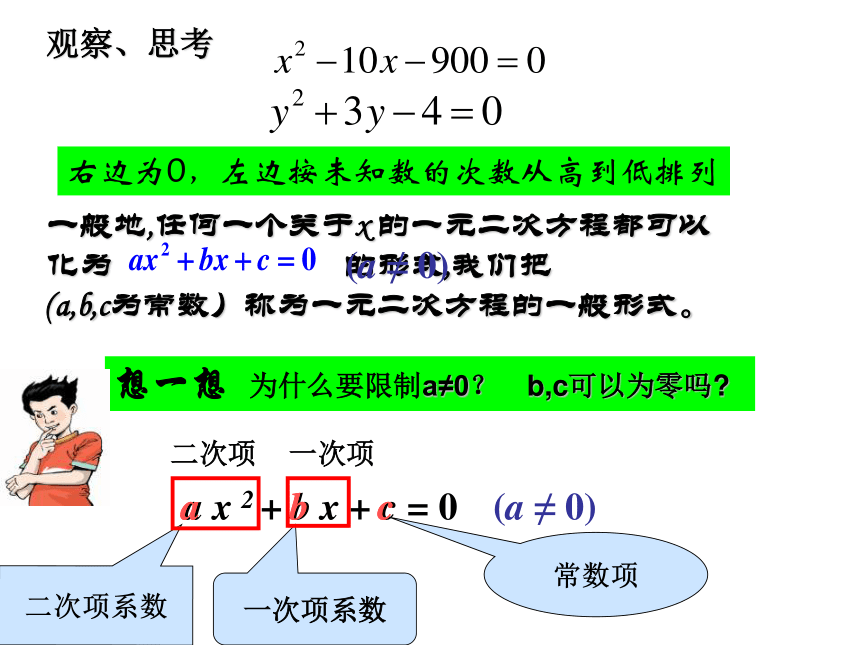
⑨2y(y-1)=y(2y+3)+3 ( ) x=0√×√×××辩一辩：×√√想一想为什么要限制a≠0？ a x 2 + b x + c = 0(a ≠ 0)aabbcc二次项系数一次项系数常数项b,c可以为零吗?上述方程形式有什么共同特点?右边为0，左边按未知数的次数从高到低排列二次项一次项观察、思考一般地,任何一个关于x 的一元二次方程都可以
化为 的形式,我们把
(a,b,c为常数）称为一元二次方程的一般形式。(a ≠ 0)判断下列方程是否为一元二次方程：① 4x2=5 ( ) ②2(x-1)=3x ( )
③2x2-3y-1=0 ( ) ④ ( )
⑤9x2=5-4x ( ) ⑥ ( )
⑦ 2a+7b=0 ( ) ⑧(2-x)(3x+4)=3 ( )
⑨2y(y-1)=y(2y+3)+3 ( ) x=0√×√×××辩一辩：×√√例1：把下列方程化成一元二次方程的一般形式，并写出它的二次项系数、一次项系数和常数项（1）4x2=5
（2）9x2=5-4x
（3）
（4）(2-x)(3x+4)=3思考: 能使一元 次方程两边相等的未知数的值叫做一元 次方程的解（或根）.你能找到使x+7=12两边相等的x的值吗?开启智慧二二一一判断未知数的值x=-1是不是方程 的解x=0呢?x=2呢? 构造一个一元二次方程，要求：
（1）常数项为零；（2）有一根为2。比如：x2-2x=0动动脑1、 是关于x一元二次方程，求a的值挑战一下2.已知关于x的一元二次方程
的一个解是x=0，则m的值是多少？挑战一下（2）若 ，你能通过观察，求出方程 的一个根吗？3.已知关于x的方程
（1）若 的一个根是1，
求 的值。挑战一下2019/2/2哪里有数，哪里就有美一元二次方程的概念
一元二次方程的一般形式
一元二次方程的解（根）的概念谈一谈本节课我们的收获......一元一次方
程的概念一元一次方程
的解的概念类比类比数学源于生活，数学服务于生活。
相信只要你处处留心，你一定会爱上数学的！