二次函数图象与性质期末复习课件
图片预览




文档简介
课件20张PPT。期末总复习
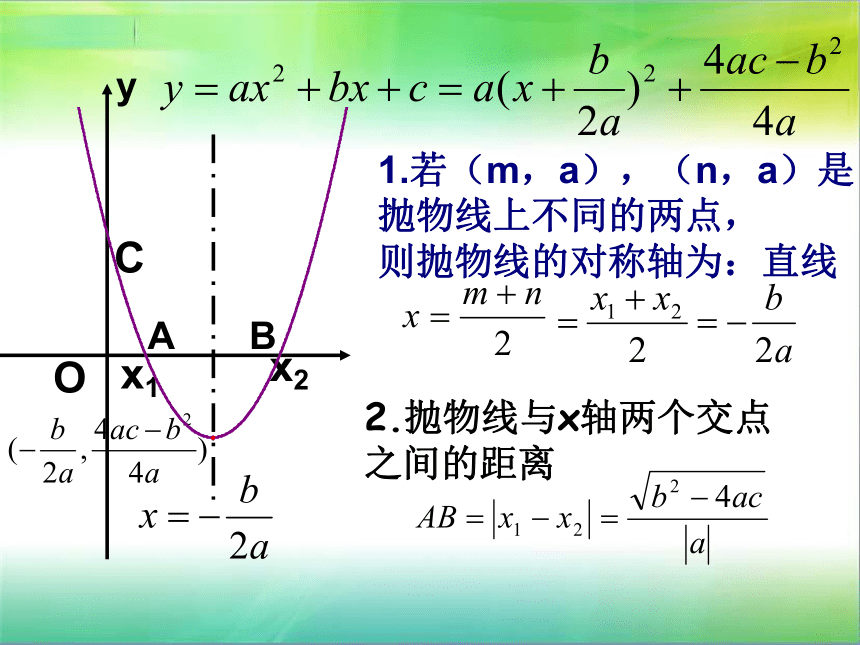
二次函数的图像与性质1.若(m,a),(n,a)是抛物线上不同的两点,
则抛物线的对称轴为:直线2.抛物线与x轴两个交点
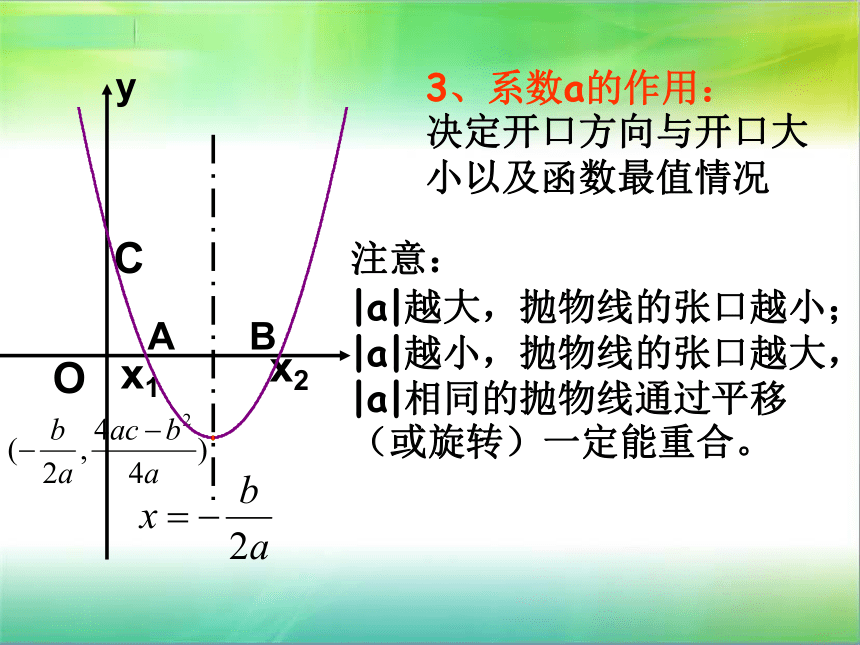
之间的距离 3、系数a的作用:
决定开口方向与开口大
小以及函数最值情况注意:
|a|越大,抛物线的张口越小;
|a|越小,抛物线的张口越大,
|a|相同的抛物线通过平移
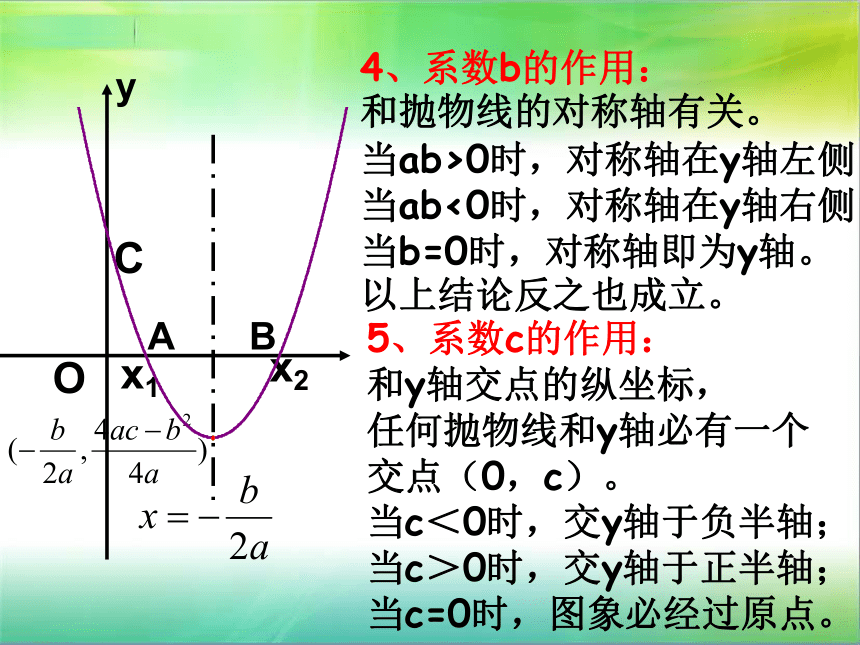
(或旋转)一定能重合。y4、系数b的作用:
和抛物线的对称轴有关。
当ab>0时,对称轴在y轴左侧
当ab<0时,对称轴在y轴右侧
当b=0时,对称轴即为y轴。
以上结论反之也成立。5、系数c的作用:
和y轴交点的纵坐标,
任何抛物线和y轴必有一个
交点(0,c)。
当c<0时,交y轴于负半轴;
当c>0时,交y轴于正半轴;
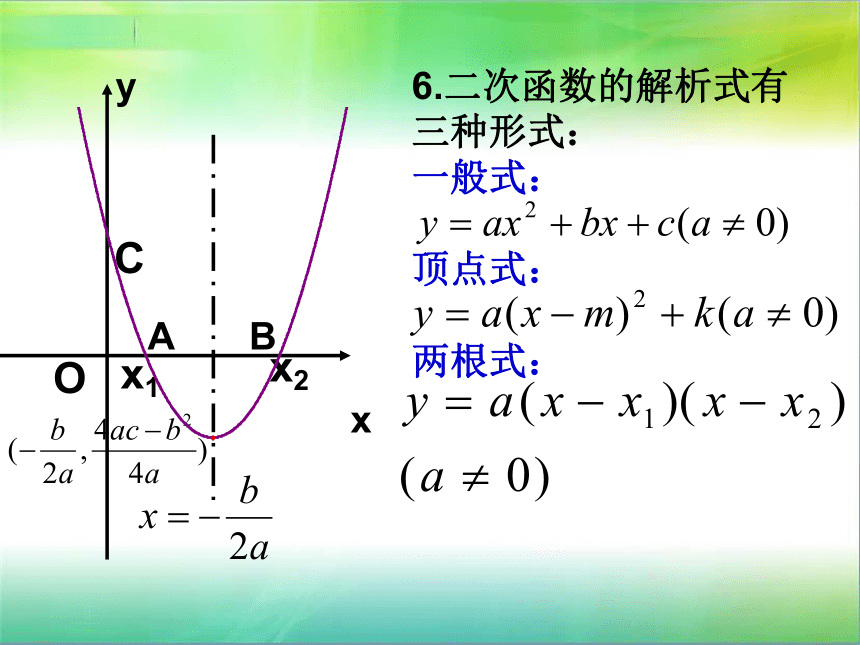
当c=0时,图象必经过原点。x6.二次函数的解析式有三种形式:
一般式:
顶点式:
两根式:例1 已知二次函数y=ax2+bx+c的图像如图所示,那么下列判断中不正确的有( )
A.abc>0
B.b2-4ac>0
C.2a+b>0
D.4a-2b+c<0-11xyo二、典型例题举例:D例2 (1)若二次函数y=x2+2(m-1)x+2m-m2的图像经过原点,求m的值
(2)若二次函数y=x2+2(m-1)x+2m-m2的图像关于y轴对称,求m的值
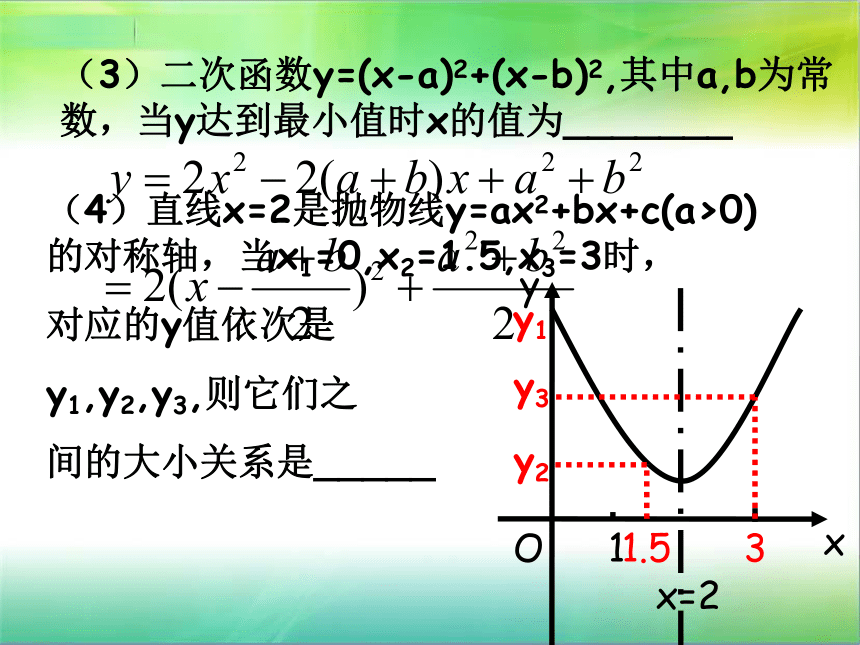
2m-m2=0,m=2或m=0(3)二次函数y=(x-a)2+(x-b)2,其中a,b为常数,当y达到最小值时x的值为_______
(4)直线x=2是抛物线y=ax2+bx+c(a>0)的对称轴,当x1=0,x2=1.5,x3=3时,
对应的y值依次是
y1,y2,y3,则它们之
间的大小关系是_____例3.求满足下列条件的二次函数解析式:
(1)二次函数的图像与x轴交于点A(2,0),
B(4,0),且图像过点C(1,6)
(2)二次函数当x=1时有最大值y=4,且x=0时
y=0
(3)二次函数的图像可由函数y=ax2-1的图像
向左平移2个单位得到,且过点M(-1,-3)
(4)图象在x轴上截得的线段长为4,图象
的顶点坐标为P(3,-2)。(5)已知抛物线C与抛物线y=2x2-4x+5关于x轴对称,求抛物线C 的解析式。xyO(1,3)Y=2(x-1)2+3(1,-3)y=2(x-1)2-3思考:若把抛物线y=2x2-4x+5绕着顶点旋转1800(6)抛物线与x轴两交点的横坐标之和为
-2.5,积为-6,且过点(0,-6)A(x1,0),B(x2,0)
x1+x2=-2.5, x1x2=-6
∴ x1,x2是方程x2+2.5x-6=0的两根
∴所求的抛物线解析式是
Y=a(x2+2.5x-6)(7)抛物线的顶点是直线y=2x与y=-2x+4的交点,且经过直线y=-2x+4与y轴的交点
(8)把抛物线y=ax2+bx+c向下平移2个单位,再向左平移6个当单位,所得的抛物线顶点为(-3,-1),且a+b+c=9,求原抛物线解析式例4已知二次函数y=-x2+(m-2)x+3 满足下列条件:
(1)图象与x轴两个交点间的距离为
(2)当x>1时,y随x增大而减小。
求m的值。变式:已知抛物线 y=-x2+(m-2)x+3与X轴交于A,B两点,与y轴交于点C,且同时满足下列条件:
(1)当x<-2时,y随x的增大而增大;
(2)当x>1时,y随x的增大而减小.
如果O是坐标原点,M是AB中点,问是否存在这样的m值,使△COM的面积等于2或6?若存在,请求出m的值;若不存在,请说明理由?
例5.已知点A(-1,-1)在抛物线
y=(k2-1)x2-2(k-2)x+1上
(1)求抛物线的对称轴;
(2)若B点与A点关于抛物线的对称轴对称,
问是否存在与抛物线只交于一点B的直线?
如果存在,求符合条件的直线;如果不存
在,说明理由。
解(2)∵ B点与A点关于抛物线的对称轴对称∴B点坐标为(x,-1),又B点在抛物线
上,解得B点坐标为K=-3,y=8x2+10x+1①当直线过点B,且与y轴平行时,满足条件,此时直线为假设存在直线y=mx+n与抛物线只交于一点B本节内容主要复习了二次函数的图象和性质,围绕解析式、图象、性质三方面展开。
(1)研究二次函数图象的关键是将函数式转换为顶点式,理解二次函数性质的关键是:充分理解图象的直观性。归纳到“三点(顶点、与坐标轴交点)一开口”。
(2)用待定系数法求二次函数的解析式,三种表达形式在不同条件下,应选择计算量少的那一种形式,通常还用到抛物线截X轴所得线段长,面积等求法。小结:例6. 已知二次函数y=x2+ax+a-2
(1)证明:不论a取何值,抛物线y=x2+ax+a-2的顶点Q总在x轴下方。
(2)设抛物线y=x2+ax+a-2与y轴交于点C,如果过点C且平行于x轴的直线与该抛物线有两个不同的交点,并设另一交点为D,问:△ACD能否是等边三角形?若能,请求出相应的二次函数解析式;若不能,请说明理由。
(3)在(2)题的已知条件下,又设抛物线与x轴的交点之一为点A,则能使△ACD的面积等于0.25的抛物线有几条?请证明的结论。7.二次函数与方程、不等式的关系思考:满足什么条件时,二次函数值恒大于0?恒小于0?
二次函数的图像与性质1.若(m,a),(n,a)是抛物线上不同的两点,
则抛物线的对称轴为:直线2.抛物线与x轴两个交点
之间的距离 3、系数a的作用:
决定开口方向与开口大
小以及函数最值情况注意:
|a|越大,抛物线的张口越小;
|a|越小,抛物线的张口越大,
|a|相同的抛物线通过平移
(或旋转)一定能重合。y4、系数b的作用:
和抛物线的对称轴有关。
当ab>0时,对称轴在y轴左侧
当ab<0时,对称轴在y轴右侧
当b=0时,对称轴即为y轴。
以上结论反之也成立。5、系数c的作用:
和y轴交点的纵坐标,
任何抛物线和y轴必有一个
交点(0,c)。
当c<0时,交y轴于负半轴;
当c>0时,交y轴于正半轴;
当c=0时,图象必经过原点。x6.二次函数的解析式有三种形式:
一般式:
顶点式:
两根式:例1 已知二次函数y=ax2+bx+c的图像如图所示,那么下列判断中不正确的有( )
A.abc>0
B.b2-4ac>0
C.2a+b>0
D.4a-2b+c<0-11xyo二、典型例题举例:D例2 (1)若二次函数y=x2+2(m-1)x+2m-m2的图像经过原点,求m的值
(2)若二次函数y=x2+2(m-1)x+2m-m2的图像关于y轴对称,求m的值
2m-m2=0,m=2或m=0(3)二次函数y=(x-a)2+(x-b)2,其中a,b为常数,当y达到最小值时x的值为_______
(4)直线x=2是抛物线y=ax2+bx+c(a>0)的对称轴,当x1=0,x2=1.5,x3=3时,
对应的y值依次是
y1,y2,y3,则它们之
间的大小关系是_____例3.求满足下列条件的二次函数解析式:
(1)二次函数的图像与x轴交于点A(2,0),
B(4,0),且图像过点C(1,6)
(2)二次函数当x=1时有最大值y=4,且x=0时
y=0
(3)二次函数的图像可由函数y=ax2-1的图像
向左平移2个单位得到,且过点M(-1,-3)
(4)图象在x轴上截得的线段长为4,图象
的顶点坐标为P(3,-2)。(5)已知抛物线C与抛物线y=2x2-4x+5关于x轴对称,求抛物线C 的解析式。xyO(1,3)Y=2(x-1)2+3(1,-3)y=2(x-1)2-3思考:若把抛物线y=2x2-4x+5绕着顶点旋转1800(6)抛物线与x轴两交点的横坐标之和为
-2.5,积为-6,且过点(0,-6)A(x1,0),B(x2,0)
x1+x2=-2.5, x1x2=-6
∴ x1,x2是方程x2+2.5x-6=0的两根
∴所求的抛物线解析式是
Y=a(x2+2.5x-6)(7)抛物线的顶点是直线y=2x与y=-2x+4的交点,且经过直线y=-2x+4与y轴的交点
(8)把抛物线y=ax2+bx+c向下平移2个单位,再向左平移6个当单位,所得的抛物线顶点为(-3,-1),且a+b+c=9,求原抛物线解析式例4已知二次函数y=-x2+(m-2)x+3 满足下列条件:
(1)图象与x轴两个交点间的距离为
(2)当x>1时,y随x增大而减小。
求m的值。变式:已知抛物线 y=-x2+(m-2)x+3与X轴交于A,B两点,与y轴交于点C,且同时满足下列条件:
(1)当x<-2时,y随x的增大而增大;
(2)当x>1时,y随x的增大而减小.
如果O是坐标原点,M是AB中点,问是否存在这样的m值,使△COM的面积等于2或6?若存在,请求出m的值;若不存在,请说明理由?
例5.已知点A(-1,-1)在抛物线
y=(k2-1)x2-2(k-2)x+1上
(1)求抛物线的对称轴;
(2)若B点与A点关于抛物线的对称轴对称,
问是否存在与抛物线只交于一点B的直线?
如果存在,求符合条件的直线;如果不存
在,说明理由。
解(2)∵ B点与A点关于抛物线的对称轴对称∴B点坐标为(x,-1),又B点在抛物线
上,解得B点坐标为K=-3,y=8x2+10x+1①当直线过点B,且与y轴平行时,满足条件,此时直线为假设存在直线y=mx+n与抛物线只交于一点B本节内容主要复习了二次函数的图象和性质,围绕解析式、图象、性质三方面展开。
(1)研究二次函数图象的关键是将函数式转换为顶点式,理解二次函数性质的关键是:充分理解图象的直观性。归纳到“三点(顶点、与坐标轴交点)一开口”。
(2)用待定系数法求二次函数的解析式,三种表达形式在不同条件下,应选择计算量少的那一种形式,通常还用到抛物线截X轴所得线段长,面积等求法。小结:例6. 已知二次函数y=x2+ax+a-2
(1)证明:不论a取何值,抛物线y=x2+ax+a-2的顶点Q总在x轴下方。
(2)设抛物线y=x2+ax+a-2与y轴交于点C,如果过点C且平行于x轴的直线与该抛物线有两个不同的交点,并设另一交点为D,问:△ACD能否是等边三角形?若能,请求出相应的二次函数解析式;若不能,请说明理由。
(3)在(2)题的已知条件下,又设抛物线与x轴的交点之一为点A,则能使△ACD的面积等于0.25的抛物线有几条?请证明的结论。7.二次函数与方程、不等式的关系思考:满足什么条件时,二次函数值恒大于0?恒小于0?
同课章节目录
