圆的切线--中考复习教案
图片预览


文档简介
辅导:圆的切线
(一)学习要求:
【学习目标】
1.了解切线的概念,探索切线与过切点的半径之间的关系.
2.能判定一条直线是否为圆的切线,理解切线的判定定理、性质定理.
3.会过圆上点画圆的切线.
【学习重点】切线判定定理、性质定理的区别与应用.
(二)知识要点:
1. 直线是圆的切线.
2.直线与⊙O相切于点A,OA是过切点的半径,直线与半径OA位置关系如何?
圆的切线 经过 的半径.
(三)例题展现:
问题1:(2012?衢州第21题)如图,在Rt△ABC中,∠C=90°,∠ABC的平分线交AC于点D,点O是AB上一点,⊙O过B、D两点,且分别交AB、BC于点E、F.
(1)求证:AC是⊙O的切线;
(2)已知AB=10,BC=6,求⊙O的半径r.
问题2:(2012?丽水第20题)如图,AB为⊙O的直径,EF切⊙O于点D,过点B作BH⊥EF于点H,交⊙O于点C,连接BD.
(1)求证:BD平分∠ABH;
(2)如果AB=12,BC=8,求圆心O到BC的距离.
(四)自我体会:
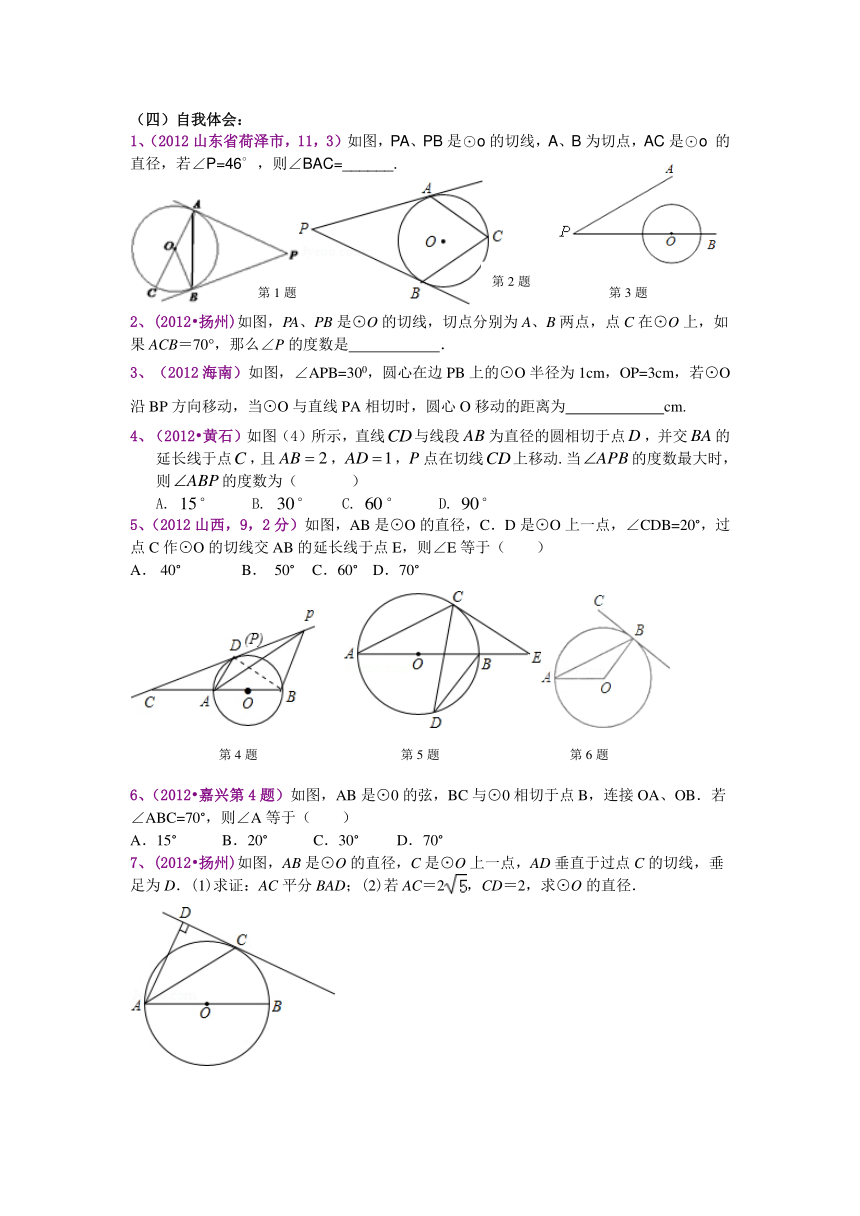
1、(2012山东省荷泽市,11,3)如图,PA、PB是⊙o的切线,A、B为切点,AC是⊙o 的直径,若∠P=46°,则∠BAC=______.
2、(2012?扬州)如图,PA、PB是⊙O的切线,切点分别为A、B两点,点C在⊙O上,如果ACB=70°,那么∠P的度数是 .
3、(2012海南)如图,∠APB=300,圆心在边PB上的⊙O半径为1cm,OP=3cm,若⊙O沿BP方向移动,当⊙O与直线PA相切时,圆心O移动的距离为 cm.
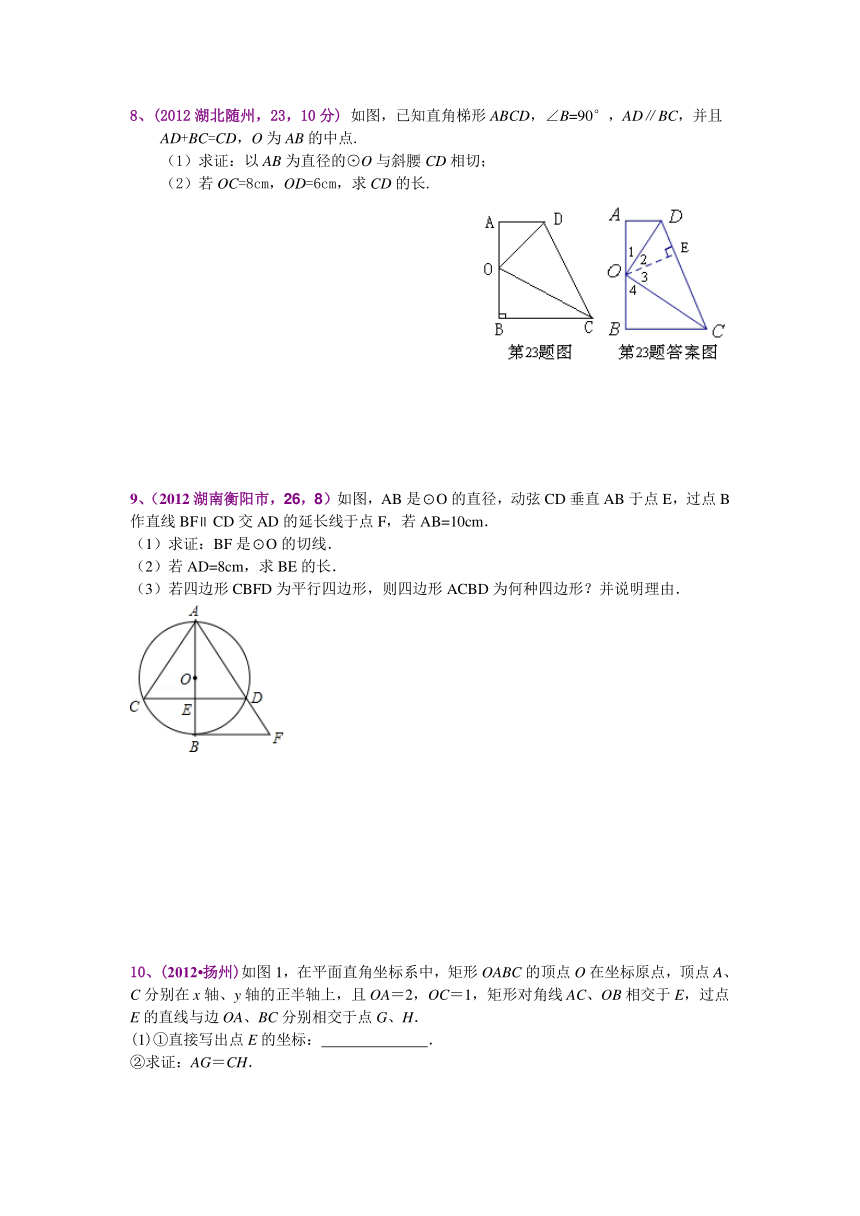
4、(2012?黄石)如图(4)所示,直线与线段为直径的圆相切于点,并交的延长线于点,且,,点在切线上移动.当的度数最大时,则的度数为( )
A. ° B. ° C. ° D. °
5、(2012山西,9,2分)如图,AB是⊙O的直径,C.D是⊙O上一点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于( )
A. 40° B. 50° C.60° D.70°
6、(2012?嘉兴第4题)如图,AB是⊙0的弦,BC与⊙0相切于点B,连接OA、OB.若∠ABC=70°,则∠A等于( )
A.15° B.20° C.30° D.70°
7、(2012?扬州)如图,AB是⊙O的直径,C是⊙O上一点,AD垂直于过点C的切线,垂足为D.(1)求证:AC平分BAD;(2)若AC=2,CD=2,求⊙O的直径.
8、(2012湖北随州,23,10分) 如图,已知直角梯形ABCD,∠B=90°,AD∥BC,并且AD+BC=CD,O为AB的中点.
(1)求证:以AB为直径的⊙O与斜腰CD相切;
(2)若OC=8cm,OD=6cm,求CD的长.
9、(2012湖南衡阳市,26,8)如图,AB是⊙O的直径,动弦CD垂直AB于点E,过点B作直线BF∥CD交AD的延长线于点F,若AB=10cm.
(1)求证:BF是⊙O的切线.
(2)若AD=8cm,求BE的长.
(3)若四边形CBFD为平行四边形,则四边形ACBD为何种四边形?并说明理由.
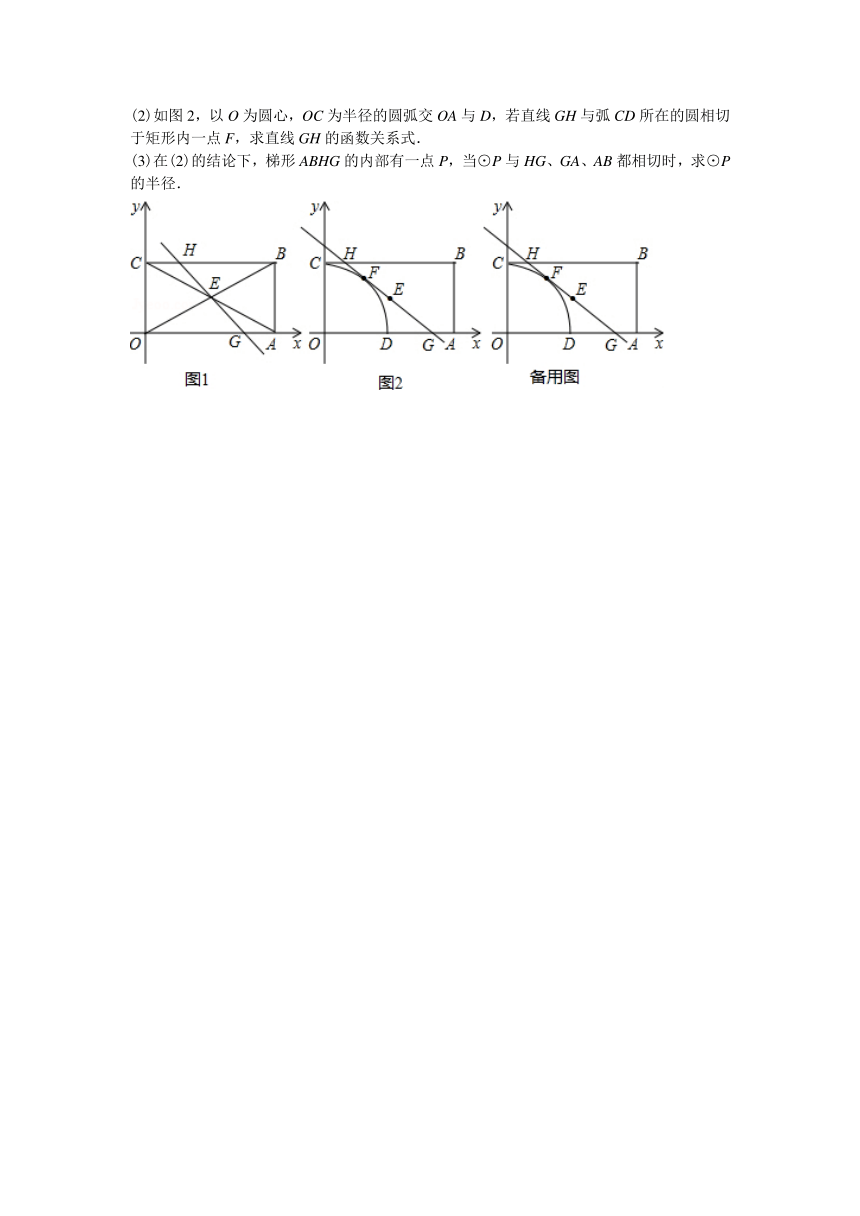
10、(2012?扬州)如图1,在平面直角坐标系中,矩形OABC的顶点O在坐标原点,顶点A、C分别在x轴、y轴的正半轴上,且OA=2,OC=1,矩形对角线AC、OB相交于E,过点E的直线与边OA、BC分别相交于点G、H.
(1)①直接写出点E的坐标: .
②求证:AG=CH.
(2)如图2,以O为圆心,OC为半径的圆弧交OA与D,若直线GH与弧CD所在的圆相切于矩形内一点F,求直线GH的函数关系式.
(3)在(2)的结论下,梯形ABHG的内部有一点P,当⊙P与HG、GA、AB都相切时,求⊙P的半径.
问题1:
考点:
切线的判定;相似三角形的判定与性质。
分析:
(1)连接OD.欲证AC是⊙O的切线,只需证明AC⊥OD即可;
(2)利用平行线截线段成比例推知=;然后将图中线段间的和差关系代入该比例式,通过解方程即可求得r的值,即⊙O的半径r的值.
解答:
(1)证明:连接OD.
∵OB=OD,∴∠OBD=∠ODB(等角对等边);
∵BD平分∠ABC,∴∠ABD=∠DBC,∴∠ODB=∠DBC(等量代换),
∴OD∥BC(内错角相等,两直线平行);
又∵∠C=90°(已知),∴∠ADO=90°(两直线平行,同位角相等),
∴AC⊥OD,即AC是⊙O的切线;
(2)解:由(1)知,OD∥BC,∴=(平行线截线段成比例),
∴=,解得r=,即⊙O的半径r为.
点评:
本题综合考查了切线的判定、平行线截线段成比例等知识点.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.
问题2:
考点:
切线的性质;勾股定理;垂径定理;圆周角定理。
分析:
(1)连接OD,根据切线的性质以及BH⊥EF,即可证得OD∥BC,然后根据等边对等角即可证得;
(2)过点O作OG⊥BC于点G,则利用垂径定理即可求得BG的长,然后在直角△OBG中利用勾股定理即可求解.
解答:
(1)证明:连接OD,
∵EF是⊙O的切线,∴OD⊥EF,
又∵BH⊥EF,∴OD∥BH,∴∠ODB=∠DBH,
∵OD=OB,∴∠ODB=∠OBD∴∠OBD=∠DBH,∴BD平分∠ABH.
(2)解:过点O作OG⊥BC于点G,则BG=CG=4,
在Rt△OBG中,OG===.
点评:
本题考查了切线的性质定理,以及勾股定理,注意到OD∥BC是关键.
(四)自我体会:
1、【解析】因为PA、PB是⊙o的切线,所以PA=PB,OA⊥PA,又因∠P=46°,所以∠PAB=67°,所以∠BAC=∠OAP-∠PAB=90°-67°=23°,
【答案】23°
【点评】当圆外一点向圆引两条切线,可以利用切线长定理及切线的性质定理,利用等腰三角形的性质及及垂直的性质来计算角的度数.
2、
考点:
切线的性质;多边形内角与外角;圆周角定理。
专题:
计算题。
分析:
连接OA,OB,由PA与PB都为圆O的切线,利用切线的性质得到OA垂直于AP,OB垂直于BP,可得出两个角为直角,再由同弧所对的圆心角等于所对圆周角的2倍,由已知∠ACB的度数求出∠AOB的度数,在四边形PABO中,根据四边形的内角和定理即可求出∠P的度数.
解答:
解:连接OA,OB,如图所示:
∵PA、PB是⊙O的切线,∴OA⊥AP,OB⊥BP,∴∠OAP=∠OBP=90°,
又∵圆心角∠AOB与圆周角∠ACB都对,且∠ACB=70°,
∴∠AOB=2∠ACB=140°,则∠P=360°-(90°+90°+140°)=40°.故答案为:40°
点评:
此题考查了切线的性质,四边形的内角与外角,以及圆周角定理,连接OA与OB,熟练运用性质及定理是解本题的关键.
3、【答案】1或5。
【考点】直线与圆相切的性质,含300角直角三角形的性质。
【分析】如图,设⊙O移动到⊙O1,⊙O2位置时与PA相切。
当⊙O移动到⊙O1时,∠O1DP=900。
∵∠APB=300,O1D=1,∴PO1=2。∵OP=3,∴OO1=1。
当⊙O移动到⊙O2时,∠O2EP=900。
∵∠APB=300,O2D=1,∴∠O2PE=300,PO2=2。
∵OP=3,∴OO1=5。
综上所述,当⊙O与PA相切时,圆心O移动的距离为1cm或5 cm。
4、【考点】切线的性质;三角形的外角性质;圆周角定理.
【分析】连接BD,有题意可知当P和D重合时,∠APB的度数最大,利用圆周角定理和直角三角形的性质即可求出∠ABP的度数.
【解答】解:连接BD,∵直线CD与以线段AB为直径的圆相切于点D,∴∠ADB=90°,
当∠APB的度数最大时,则P和D重合,∴∠APB=90°,
∵AB=2,AD=1,∴sin∠DBP=AD/AB =1/2 ,∴∠ABP=30°,
∴当∠APB的度数最大时,∠ABP的度数为30°.故选B.
【点评】本题考查了切线的性质,圆周角定理以及解直角三角形的有关知识,解题的关键是有题意可知当P和D重合时,∠APB的度数最大为90°.(圆内角>圆周角>圆外角)
5、【解析】解:连接OC,如图所示:
∵圆心角∠BOC与圆周角∠CBD都对,∴∠BOC=2∠CBD,又∠CDB=20°,
∴∠BOC=40°,又∵CE为圆O的切线,∴OC⊥CE,即∠OCE=90°,
则∠E=90°﹣40°=50°.故选B
【点评】本题主要考查了圆的切线的性质、同圆中同弧所对的圆周角相等及等边对等角等性质;解决本题的关键是熟悉圆中常见辅助线作法及相关性质.难度中等.
6、
考点:
切线的性质。
分析:
由BC与⊙0相切于点B,根据切线的性质,即可求得∠OBC=90°,又由∠ABC=70°,即可求得∠OBA的度数,然后由OA=OB,利用等边对等角的知识,即可求得∠A的度数.
解答:
解:∵BC与⊙0相切于点B,∴OB⊥BC,∴∠OBC=90°,
∵∠ABC=70°,∴∠OBA=∠OBC﹣∠ABC=90°﹣70°=20°,
∵OA=OB,∴∠A=∠OBA=20°.故选B.
点评:
此题考查了切线的性质与等腰三角形的性质.此题比较简单,注意数形结合思想的应用,注意圆的切线垂直于经过切点的半径定理的应用.
7、
考点:
切线的性质;角平分线的性质;勾股定理;相似三角形的判定与性质。
专题:
计算题。
分析:
(1)连接OC,根据切线的性质判断出AD∥OC,得到∠DAC=∠OCA,再根据OA=OC得到∠OAC=∠OCA,
可得AC平分∠BAD.
(2)连接BC,得到△ADC∽△ACB,根据相似三角形的性质即可求出AB的长.
解答:
解:(1)如图:连接OC,
∵DC切⊙O于C,∴AD⊥CD,∴∠ADC=∠OCF=90°,∴AD∥OC,
∴∠DAC=∠OCA,
∵OA=OC,∴∠OAC=∠OCA,即AC平分∠BAD.
(2)连接BC.
∵AB是直径,∴∠ACB=90°=∠ADC,
∵∠OAC=∠OCA,∴△ADC∽△ACB,∴,
在Rt△ADC中,AC=2,CD=2,∴AD=4,∴,∴AB=5.
8、解析:(1)过AB的中点O作OE⊥CD于E.证明OE的长等于半径即可.(2)证明∠COD=900,运用勾股定理求值..
答案:证明: 过AB的中点O作OE⊥CD于E.
S梯形ABCD=(AD+BC) ?AB=(AD+BC) ?OA=2(AD?OA+BC?OB)
=2(S⊿OAD +S⊿OBC)
由S梯形ABCD =S⊿OBC+ S⊿OAD+ S⊿OCD∴S⊿OBC+ S⊿OAD=S⊿OCD
∴AD?OA+BC?OA=CD·OE
∴(AD+BC) ·OA=CD·OE又AD+BC=CD
∴OA=OE,∴E点在以AB为直径的⊙O上,又OE⊥CD∴CD是⊙O的切线
即:CD与⊙O相切 …………5分
(2)∵DA、DE均为⊙O的切线,∴DA=DE,则∠1=∠2,同理∠3=∠4. ∴∠COD=900.
∴CD= …………5分
点评:本题考查梯形、直线余与圆的位置关系、勾股定理.根据圆的切线的定义准确的作出辅助线是解决问题的关键.本题中运用面积法证明AD+BC=CD很巧妙.难度较大.
9、解析:(1)欲证明BF是⊙O的切线,只需证明AB⊥BF即可;
(2)连接BD,在直角三角形ABD中,利用摄影定理可以求得AE的长度,最后结合图形知BE=AB﹣AE;
(3)连接BC.四边形CBFD为平行四边形,则四边形ACBD是正方形.根据平行四边形的对边平行、平行线的性质、圆周角定理以及同弧所对的圆周角相等可以推知∠CAD=∠BDA=90°,即CD是⊙O的直径,然后由全等三角形的判定与性质推知AC=BD;根据正方形的判定定理证得四边形ACBD是正方形.
答案:解:(1)∵AB是⊙O的直径,CD⊥AB,BF∥CD,
∴BF⊥AB,即BF是⊙O的切线;
(2)如图1,连接BD.∵AB是⊙O的直径,∴∠ADB=90°(直径所对的圆周角是直角);
又∵DE⊥AB∴AD2=AE?AB;
∵AD=8cm,AB=10cm,AE=6.4cm,∴BE=AB﹣AE=3.6cm;
(3)连接BC.
四边形CBFD为平行四边形,则四边形ACBD是正方形.理由如下:
∵四边形CBFD为平行四边形,∴BC∥FD,即BC∥AD;
∴∠BCD=∠ADC(两直线平行,内错角相等),
∵∠BCD=∠BAD,∠CAB=∠CDB,(同弧所对的圆周角相等),
∴∠CAB+∠BAD=∠CDB+∠ADC,即∠CAD=∠BDA;
又∵∠BDA=90°(直径所对的圆周角是直角),∴∠CAD=∠BDA=90°,
∴CD是⊙O的直径,即点E与点O重合(或线段CD过圆形O),如图2,
在△OBC和△ODA中,
∵,∴△OBC≌△ODA(SAS),
∴BC=DA(全等三角形的对应边相等),
∴四边形ACBD是平行四边形(对边平行且相等的四边形是平行四边形);
∵∠ACB=90°(直径所对的圆周角是直角),AC=AD,∴四边形ACBD是正方形.
10、
考点:
切线的判定与性质;一次函数综合题;全等三角形的判定与性质;勾股定理;矩形的性质;相似三角形的判定与性质。
专题:
计算题;证明题。
解答:
(1)①解:E的坐标是:(1,),
②证明:∵矩形OABC,∴CE=AE,BC∥OA,∴∠HCE=∠EAG,
∵在△CHE和△AGE中,∴△CHE≌△AGE,∴AG=CH.
(2)解:连接DE并延长DE交CB于M,
∵DD=OC=1=OA,∴D是OA的中点,
∵在△CME和△ADE中,∴△CME≌△ADE,
∴CM=AD=2-1=1,
∵BC∥OA,∠COD=90°,∴四边形CMDO是矩形,∴MD⊥OD,MD⊥CB,
∴MD切⊙O于D,
∵得HG切⊙O于F,E(1,),∴可设CH=HF=x,FE=ED==ME,
在Rt△MHE中,有MH2+ME2=HE2
即(1-x)2+()2=(+x)2,解得x=,∴H(,1),OG=2-=,
又∵G(,0),设直线GH的解析式是:y=kx+b,
把G、H的坐标代入得:0=b,且1=k+b,得:k=-,b=,
∴直线GH的函数关系式为y=-.
(3)解:连接BG,
∵在△OCH和△BAG中,∴△OCH≌△BAG,
∴∠CHO=∠AGB,
∵∠HCO=90°,∴HC切⊙O于C,HG切⊙O于F,∴OH平分∠CHF,
∴∠CHO=∠FHO=∠BGA,
∵△CHE≌△AGE,∴HE=GE,
在△HOE和△GBE中,∴△HOE≌△GBE,
∴∠OHE=∠BGE,21世纪教育网
∵∠CHO=∠FHO=∠BGA,∴∠BGA=∠BGE,即BG平分∠FGA,
∵⊙P与HG、GA、AB都相切,∴圆心P必在BG上,
过P做PN⊥GA,垂足为N,∴△GPN∽△GBA,∴,
设半径为r,=,解得:r=,答:⊙P的半径是.
点评:
本题综合考查了矩形的性质和判定,全等三角形的性质和判定,相似三角形的性质和判定,切线的性质和判定,一次函数和勾股定理等知识点,本题综合性比较强,难度偏大,但是也是一道比较好的题目.
辅导:圆的切线
(一)学习要求:
【学习目标】
1.了解切线的概念,探索切线与过切点的半径之间的关系.
2.能判定一条直线是否为圆的切线,理解切线的判定定理、性质定理.
3.会过圆上点画圆的切线.
【学习重点】切线判定定理、性质定理的区别与应用.
(二)知识要点:
1. 直线是圆的切线.
2.直线与⊙O相切于点A,OA是过切点的半径,直线与半径OA位置关系如何?
圆的切线 经过 的半径.
(三)例题展现:
问题1:(2012?衢州第21题)如图,在Rt△ABC中,∠C=90°,∠ABC的平分线交AC于点D,点O是AB上一点,⊙O过B、D两点,且分别交AB、BC于点E、F.
(1)求证:AC是⊙O的切线;
(2)已知AB=10,BC=6,求⊙O的半径r.
问题2:(2012?丽水第20题)如图,AB为⊙O的直径,EF切⊙O于点D,过点B作BH⊥EF于点H,交⊙O于点C,连接BD.
(1)求证:BD平分∠ABH;
(2)如果AB=12,BC=8,求圆心O到BC的距离.
(四)自我体会:
1、(2012山东省荷泽市,11,3)如图,PA、PB是⊙o的切线,A、B为切点,AC是⊙o 的直径,若∠P=46°,则∠BAC=______.
2、(2012?扬州)如图,PA、PB是⊙O的切线,切点分别为A、B两点,点C在⊙O上,如果ACB=70°,那么∠P的度数是 .
3、(2012海南)如图,∠APB=300,圆心在边PB上的⊙O半径为1cm,OP=3cm,若⊙O沿BP方向移动,当⊙O与直线PA相切时,圆心O移动的距离为 cm.
4、(2012?黄石)如图(4)所示,直线与线段为直径的圆相切于点,并交的延长线于点,且,,点在切线上移动.当的度数最大时,则的度数为( )
A. ° B. ° C. ° D. °
5、(2012山西,9,2分)如图,AB是⊙O的直径,C.D是⊙O上一点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于( )
A. 40° B. 50° C.60° D.70°
6、(2012?嘉兴第4题)如图,AB是⊙0的弦,BC与⊙0相切于点B,连接OA、OB.若∠ABC=70°,则∠A等于( )
A.15° B.20° C.30° D.70°
7、(2012?扬州)如图,AB是⊙O的直径,C是⊙O上一点,AD垂直于过点C的切线,垂足为D.(1)求证:AC平分BAD;(2)若AC=2,CD=2,求⊙O的直径.
8、(2012湖北随州,23,10分) 如图,已知直角梯形ABCD,∠B=90°,AD∥BC,并且AD+BC=CD,O为AB的中点.
(1)求证:以AB为直径的⊙O与斜腰CD相切;
(2)若OC=8cm,OD=6cm,求CD的长.
9、(2012湖南衡阳市,26,8)如图,AB是⊙O的直径,动弦CD垂直AB于点E,过点B作直线BF∥CD交AD的延长线于点F,若AB=10cm.
(1)求证:BF是⊙O的切线.
(2)若AD=8cm,求BE的长.
(3)若四边形CBFD为平行四边形,则四边形ACBD为何种四边形?并说明理由.
10、(2012?扬州)如图1,在平面直角坐标系中,矩形OABC的顶点O在坐标原点,顶点A、C分别在x轴、y轴的正半轴上,且OA=2,OC=1,矩形对角线AC、OB相交于E,过点E的直线与边OA、BC分别相交于点G、H.
(1)①直接写出点E的坐标: .
②求证:AG=CH.
(2)如图2,以O为圆心,OC为半径的圆弧交OA与D,若直线GH与弧CD所在的圆相切于矩形内一点F,求直线GH的函数关系式.
(3)在(2)的结论下,梯形ABHG的内部有一点P,当⊙P与HG、GA、AB都相切时,求⊙P的半径.
问题1:
考点:
切线的判定;相似三角形的判定与性质。
分析:
(1)连接OD.欲证AC是⊙O的切线,只需证明AC⊥OD即可;
(2)利用平行线截线段成比例推知=;然后将图中线段间的和差关系代入该比例式,通过解方程即可求得r的值,即⊙O的半径r的值.
解答:
(1)证明:连接OD.
∵OB=OD,∴∠OBD=∠ODB(等角对等边);
∵BD平分∠ABC,∴∠ABD=∠DBC,∴∠ODB=∠DBC(等量代换),
∴OD∥BC(内错角相等,两直线平行);
又∵∠C=90°(已知),∴∠ADO=90°(两直线平行,同位角相等),
∴AC⊥OD,即AC是⊙O的切线;
(2)解:由(1)知,OD∥BC,∴=(平行线截线段成比例),
∴=,解得r=,即⊙O的半径r为.
点评:
本题综合考查了切线的判定、平行线截线段成比例等知识点.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.
问题2:
考点:
切线的性质;勾股定理;垂径定理;圆周角定理。
分析:
(1)连接OD,根据切线的性质以及BH⊥EF,即可证得OD∥BC,然后根据等边对等角即可证得;
(2)过点O作OG⊥BC于点G,则利用垂径定理即可求得BG的长,然后在直角△OBG中利用勾股定理即可求解.
解答:
(1)证明:连接OD,
∵EF是⊙O的切线,∴OD⊥EF,
又∵BH⊥EF,∴OD∥BH,∴∠ODB=∠DBH,
∵OD=OB,∴∠ODB=∠OBD∴∠OBD=∠DBH,∴BD平分∠ABH.
(2)解:过点O作OG⊥BC于点G,则BG=CG=4,
在Rt△OBG中,OG===.
点评:
本题考查了切线的性质定理,以及勾股定理,注意到OD∥BC是关键.
(四)自我体会:
1、【解析】因为PA、PB是⊙o的切线,所以PA=PB,OA⊥PA,又因∠P=46°,所以∠PAB=67°,所以∠BAC=∠OAP-∠PAB=90°-67°=23°,
【答案】23°
【点评】当圆外一点向圆引两条切线,可以利用切线长定理及切线的性质定理,利用等腰三角形的性质及及垂直的性质来计算角的度数.
2、
考点:
切线的性质;多边形内角与外角;圆周角定理。
专题:
计算题。
分析:
连接OA,OB,由PA与PB都为圆O的切线,利用切线的性质得到OA垂直于AP,OB垂直于BP,可得出两个角为直角,再由同弧所对的圆心角等于所对圆周角的2倍,由已知∠ACB的度数求出∠AOB的度数,在四边形PABO中,根据四边形的内角和定理即可求出∠P的度数.
解答:
解:连接OA,OB,如图所示:
∵PA、PB是⊙O的切线,∴OA⊥AP,OB⊥BP,∴∠OAP=∠OBP=90°,
又∵圆心角∠AOB与圆周角∠ACB都对,且∠ACB=70°,
∴∠AOB=2∠ACB=140°,则∠P=360°-(90°+90°+140°)=40°.故答案为:40°
点评:
此题考查了切线的性质,四边形的内角与外角,以及圆周角定理,连接OA与OB,熟练运用性质及定理是解本题的关键.
3、【答案】1或5。
【考点】直线与圆相切的性质,含300角直角三角形的性质。
【分析】如图,设⊙O移动到⊙O1,⊙O2位置时与PA相切。
当⊙O移动到⊙O1时,∠O1DP=900。
∵∠APB=300,O1D=1,∴PO1=2。∵OP=3,∴OO1=1。
当⊙O移动到⊙O2时,∠O2EP=900。
∵∠APB=300,O2D=1,∴∠O2PE=300,PO2=2。
∵OP=3,∴OO1=5。
综上所述,当⊙O与PA相切时,圆心O移动的距离为1cm或5 cm。
4、【考点】切线的性质;三角形的外角性质;圆周角定理.
【分析】连接BD,有题意可知当P和D重合时,∠APB的度数最大,利用圆周角定理和直角三角形的性质即可求出∠ABP的度数.
【解答】解:连接BD,∵直线CD与以线段AB为直径的圆相切于点D,∴∠ADB=90°,
当∠APB的度数最大时,则P和D重合,∴∠APB=90°,
∵AB=2,AD=1,∴sin∠DBP=AD/AB =1/2 ,∴∠ABP=30°,
∴当∠APB的度数最大时,∠ABP的度数为30°.故选B.
【点评】本题考查了切线的性质,圆周角定理以及解直角三角形的有关知识,解题的关键是有题意可知当P和D重合时,∠APB的度数最大为90°.(圆内角>圆周角>圆外角)
5、【解析】解:连接OC,如图所示:
∵圆心角∠BOC与圆周角∠CBD都对,∴∠BOC=2∠CBD,又∠CDB=20°,
∴∠BOC=40°,又∵CE为圆O的切线,∴OC⊥CE,即∠OCE=90°,
则∠E=90°﹣40°=50°.故选B
【点评】本题主要考查了圆的切线的性质、同圆中同弧所对的圆周角相等及等边对等角等性质;解决本题的关键是熟悉圆中常见辅助线作法及相关性质.难度中等.
6、
考点:
切线的性质。
分析:
由BC与⊙0相切于点B,根据切线的性质,即可求得∠OBC=90°,又由∠ABC=70°,即可求得∠OBA的度数,然后由OA=OB,利用等边对等角的知识,即可求得∠A的度数.
解答:
解:∵BC与⊙0相切于点B,∴OB⊥BC,∴∠OBC=90°,
∵∠ABC=70°,∴∠OBA=∠OBC﹣∠ABC=90°﹣70°=20°,
∵OA=OB,∴∠A=∠OBA=20°.故选B.
点评:
此题考查了切线的性质与等腰三角形的性质.此题比较简单,注意数形结合思想的应用,注意圆的切线垂直于经过切点的半径定理的应用.
7、
考点:
切线的性质;角平分线的性质;勾股定理;相似三角形的判定与性质。
专题:
计算题。
分析:
(1)连接OC,根据切线的性质判断出AD∥OC,得到∠DAC=∠OCA,再根据OA=OC得到∠OAC=∠OCA,
可得AC平分∠BAD.
(2)连接BC,得到△ADC∽△ACB,根据相似三角形的性质即可求出AB的长.
解答:
解:(1)如图:连接OC,
∵DC切⊙O于C,∴AD⊥CD,∴∠ADC=∠OCF=90°,∴AD∥OC,
∴∠DAC=∠OCA,
∵OA=OC,∴∠OAC=∠OCA,即AC平分∠BAD.
(2)连接BC.
∵AB是直径,∴∠ACB=90°=∠ADC,
∵∠OAC=∠OCA,∴△ADC∽△ACB,∴,
在Rt△ADC中,AC=2,CD=2,∴AD=4,∴,∴AB=5.
8、解析:(1)过AB的中点O作OE⊥CD于E.证明OE的长等于半径即可.(2)证明∠COD=900,运用勾股定理求值..
答案:证明: 过AB的中点O作OE⊥CD于E.
S梯形ABCD=(AD+BC) ?AB=(AD+BC) ?OA=2(AD?OA+BC?OB)
=2(S⊿OAD +S⊿OBC)
由S梯形ABCD =S⊿OBC+ S⊿OAD+ S⊿OCD∴S⊿OBC+ S⊿OAD=S⊿OCD
∴AD?OA+BC?OA=CD·OE
∴(AD+BC) ·OA=CD·OE又AD+BC=CD
∴OA=OE,∴E点在以AB为直径的⊙O上,又OE⊥CD∴CD是⊙O的切线
即:CD与⊙O相切 …………5分
(2)∵DA、DE均为⊙O的切线,∴DA=DE,则∠1=∠2,同理∠3=∠4. ∴∠COD=900.
∴CD= …………5分
点评:本题考查梯形、直线余与圆的位置关系、勾股定理.根据圆的切线的定义准确的作出辅助线是解决问题的关键.本题中运用面积法证明AD+BC=CD很巧妙.难度较大.
9、解析:(1)欲证明BF是⊙O的切线,只需证明AB⊥BF即可;
(2)连接BD,在直角三角形ABD中,利用摄影定理可以求得AE的长度,最后结合图形知BE=AB﹣AE;
(3)连接BC.四边形CBFD为平行四边形,则四边形ACBD是正方形.根据平行四边形的对边平行、平行线的性质、圆周角定理以及同弧所对的圆周角相等可以推知∠CAD=∠BDA=90°,即CD是⊙O的直径,然后由全等三角形的判定与性质推知AC=BD;根据正方形的判定定理证得四边形ACBD是正方形.
答案:解:(1)∵AB是⊙O的直径,CD⊥AB,BF∥CD,
∴BF⊥AB,即BF是⊙O的切线;
(2)如图1,连接BD.∵AB是⊙O的直径,∴∠ADB=90°(直径所对的圆周角是直角);
又∵DE⊥AB∴AD2=AE?AB;
∵AD=8cm,AB=10cm,AE=6.4cm,∴BE=AB﹣AE=3.6cm;
(3)连接BC.
四边形CBFD为平行四边形,则四边形ACBD是正方形.理由如下:
∵四边形CBFD为平行四边形,∴BC∥FD,即BC∥AD;
∴∠BCD=∠ADC(两直线平行,内错角相等),
∵∠BCD=∠BAD,∠CAB=∠CDB,(同弧所对的圆周角相等),
∴∠CAB+∠BAD=∠CDB+∠ADC,即∠CAD=∠BDA;
又∵∠BDA=90°(直径所对的圆周角是直角),∴∠CAD=∠BDA=90°,
∴CD是⊙O的直径,即点E与点O重合(或线段CD过圆形O),如图2,
在△OBC和△ODA中,
∵,∴△OBC≌△ODA(SAS),
∴BC=DA(全等三角形的对应边相等),
∴四边形ACBD是平行四边形(对边平行且相等的四边形是平行四边形);
∵∠ACB=90°(直径所对的圆周角是直角),AC=AD,∴四边形ACBD是正方形.
10、
考点:
切线的判定与性质;一次函数综合题;全等三角形的判定与性质;勾股定理;矩形的性质;相似三角形的判定与性质。
专题:
计算题;证明题。
解答:
(1)①解:E的坐标是:(1,),
②证明:∵矩形OABC,∴CE=AE,BC∥OA,∴∠HCE=∠EAG,
∵在△CHE和△AGE中,∴△CHE≌△AGE,∴AG=CH.
(2)解:连接DE并延长DE交CB于M,
∵DD=OC=1=OA,∴D是OA的中点,
∵在△CME和△ADE中,∴△CME≌△ADE,
∴CM=AD=2-1=1,
∵BC∥OA,∠COD=90°,∴四边形CMDO是矩形,∴MD⊥OD,MD⊥CB,
∴MD切⊙O于D,
∵得HG切⊙O于F,E(1,),∴可设CH=HF=x,FE=ED==ME,
在Rt△MHE中,有MH2+ME2=HE2
即(1-x)2+()2=(+x)2,解得x=,∴H(,1),OG=2-=,
又∵G(,0),设直线GH的解析式是:y=kx+b,
把G、H的坐标代入得:0=b,且1=k+b,得:k=-,b=,
∴直线GH的函数关系式为y=-.
(3)解:连接BG,
∵在△OCH和△BAG中,∴△OCH≌△BAG,
∴∠CHO=∠AGB,
∵∠HCO=90°,∴HC切⊙O于C,HG切⊙O于F,∴OH平分∠CHF,
∴∠CHO=∠FHO=∠BGA,
∵△CHE≌△AGE,∴HE=GE,
在△HOE和△GBE中,∴△HOE≌△GBE,
∴∠OHE=∠BGE,21世纪教育网
∵∠CHO=∠FHO=∠BGA,∴∠BGA=∠BGE,即BG平分∠FGA,
∵⊙P与HG、GA、AB都相切,∴圆心P必在BG上,
过P做PN⊥GA,垂足为N,∴△GPN∽△GBA,∴,
设半径为r,=,解得:r=,答:⊙P的半径是.
点评:
本题综合考查了矩形的性质和判定,全等三角形的性质和判定,相似三角形的性质和判定,切线的性质和判定,一次函数和勾股定理等知识点,本题综合性比较强,难度偏大,但是也是一道比较好的题目.
(一)学习要求:
【学习目标】
1.了解切线的概念,探索切线与过切点的半径之间的关系.
2.能判定一条直线是否为圆的切线,理解切线的判定定理、性质定理.
3.会过圆上点画圆的切线.
【学习重点】切线判定定理、性质定理的区别与应用.
(二)知识要点:
1. 直线是圆的切线.
2.直线与⊙O相切于点A,OA是过切点的半径,直线与半径OA位置关系如何?
圆的切线 经过 的半径.
(三)例题展现:
问题1:(2012?衢州第21题)如图,在Rt△ABC中,∠C=90°,∠ABC的平分线交AC于点D,点O是AB上一点,⊙O过B、D两点,且分别交AB、BC于点E、F.
(1)求证:AC是⊙O的切线;
(2)已知AB=10,BC=6,求⊙O的半径r.
问题2:(2012?丽水第20题)如图,AB为⊙O的直径,EF切⊙O于点D,过点B作BH⊥EF于点H,交⊙O于点C,连接BD.
(1)求证:BD平分∠ABH;
(2)如果AB=12,BC=8,求圆心O到BC的距离.
(四)自我体会:
1、(2012山东省荷泽市,11,3)如图,PA、PB是⊙o的切线,A、B为切点,AC是⊙o 的直径,若∠P=46°,则∠BAC=______.
2、(2012?扬州)如图,PA、PB是⊙O的切线,切点分别为A、B两点,点C在⊙O上,如果ACB=70°,那么∠P的度数是 .
3、(2012海南)如图,∠APB=300,圆心在边PB上的⊙O半径为1cm,OP=3cm,若⊙O沿BP方向移动,当⊙O与直线PA相切时,圆心O移动的距离为 cm.
4、(2012?黄石)如图(4)所示,直线与线段为直径的圆相切于点,并交的延长线于点,且,,点在切线上移动.当的度数最大时,则的度数为( )
A. ° B. ° C. ° D. °
5、(2012山西,9,2分)如图,AB是⊙O的直径,C.D是⊙O上一点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于( )
A. 40° B. 50° C.60° D.70°
6、(2012?嘉兴第4题)如图,AB是⊙0的弦,BC与⊙0相切于点B,连接OA、OB.若∠ABC=70°,则∠A等于( )
A.15° B.20° C.30° D.70°
7、(2012?扬州)如图,AB是⊙O的直径,C是⊙O上一点,AD垂直于过点C的切线,垂足为D.(1)求证:AC平分BAD;(2)若AC=2,CD=2,求⊙O的直径.
8、(2012湖北随州,23,10分) 如图,已知直角梯形ABCD,∠B=90°,AD∥BC,并且AD+BC=CD,O为AB的中点.
(1)求证:以AB为直径的⊙O与斜腰CD相切;
(2)若OC=8cm,OD=6cm,求CD的长.
9、(2012湖南衡阳市,26,8)如图,AB是⊙O的直径,动弦CD垂直AB于点E,过点B作直线BF∥CD交AD的延长线于点F,若AB=10cm.
(1)求证:BF是⊙O的切线.
(2)若AD=8cm,求BE的长.
(3)若四边形CBFD为平行四边形,则四边形ACBD为何种四边形?并说明理由.
10、(2012?扬州)如图1,在平面直角坐标系中,矩形OABC的顶点O在坐标原点,顶点A、C分别在x轴、y轴的正半轴上,且OA=2,OC=1,矩形对角线AC、OB相交于E,过点E的直线与边OA、BC分别相交于点G、H.
(1)①直接写出点E的坐标: .
②求证:AG=CH.
(2)如图2,以O为圆心,OC为半径的圆弧交OA与D,若直线GH与弧CD所在的圆相切于矩形内一点F,求直线GH的函数关系式.
(3)在(2)的结论下,梯形ABHG的内部有一点P,当⊙P与HG、GA、AB都相切时,求⊙P的半径.
问题1:
考点:
切线的判定;相似三角形的判定与性质。
分析:
(1)连接OD.欲证AC是⊙O的切线,只需证明AC⊥OD即可;
(2)利用平行线截线段成比例推知=;然后将图中线段间的和差关系代入该比例式,通过解方程即可求得r的值,即⊙O的半径r的值.
解答:
(1)证明:连接OD.
∵OB=OD,∴∠OBD=∠ODB(等角对等边);
∵BD平分∠ABC,∴∠ABD=∠DBC,∴∠ODB=∠DBC(等量代换),
∴OD∥BC(内错角相等,两直线平行);
又∵∠C=90°(已知),∴∠ADO=90°(两直线平行,同位角相等),
∴AC⊥OD,即AC是⊙O的切线;
(2)解:由(1)知,OD∥BC,∴=(平行线截线段成比例),
∴=,解得r=,即⊙O的半径r为.
点评:
本题综合考查了切线的判定、平行线截线段成比例等知识点.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.
问题2:
考点:
切线的性质;勾股定理;垂径定理;圆周角定理。
分析:
(1)连接OD,根据切线的性质以及BH⊥EF,即可证得OD∥BC,然后根据等边对等角即可证得;
(2)过点O作OG⊥BC于点G,则利用垂径定理即可求得BG的长,然后在直角△OBG中利用勾股定理即可求解.
解答:
(1)证明:连接OD,
∵EF是⊙O的切线,∴OD⊥EF,
又∵BH⊥EF,∴OD∥BH,∴∠ODB=∠DBH,
∵OD=OB,∴∠ODB=∠OBD∴∠OBD=∠DBH,∴BD平分∠ABH.
(2)解:过点O作OG⊥BC于点G,则BG=CG=4,
在Rt△OBG中,OG===.
点评:
本题考查了切线的性质定理,以及勾股定理,注意到OD∥BC是关键.
(四)自我体会:
1、【解析】因为PA、PB是⊙o的切线,所以PA=PB,OA⊥PA,又因∠P=46°,所以∠PAB=67°,所以∠BAC=∠OAP-∠PAB=90°-67°=23°,
【答案】23°
【点评】当圆外一点向圆引两条切线,可以利用切线长定理及切线的性质定理,利用等腰三角形的性质及及垂直的性质来计算角的度数.
2、
考点:
切线的性质;多边形内角与外角;圆周角定理。
专题:
计算题。
分析:
连接OA,OB,由PA与PB都为圆O的切线,利用切线的性质得到OA垂直于AP,OB垂直于BP,可得出两个角为直角,再由同弧所对的圆心角等于所对圆周角的2倍,由已知∠ACB的度数求出∠AOB的度数,在四边形PABO中,根据四边形的内角和定理即可求出∠P的度数.
解答:
解:连接OA,OB,如图所示:
∵PA、PB是⊙O的切线,∴OA⊥AP,OB⊥BP,∴∠OAP=∠OBP=90°,
又∵圆心角∠AOB与圆周角∠ACB都对,且∠ACB=70°,
∴∠AOB=2∠ACB=140°,则∠P=360°-(90°+90°+140°)=40°.故答案为:40°
点评:
此题考查了切线的性质,四边形的内角与外角,以及圆周角定理,连接OA与OB,熟练运用性质及定理是解本题的关键.
3、【答案】1或5。
【考点】直线与圆相切的性质,含300角直角三角形的性质。
【分析】如图,设⊙O移动到⊙O1,⊙O2位置时与PA相切。
当⊙O移动到⊙O1时,∠O1DP=900。
∵∠APB=300,O1D=1,∴PO1=2。∵OP=3,∴OO1=1。
当⊙O移动到⊙O2时,∠O2EP=900。
∵∠APB=300,O2D=1,∴∠O2PE=300,PO2=2。
∵OP=3,∴OO1=5。
综上所述,当⊙O与PA相切时,圆心O移动的距离为1cm或5 cm。
4、【考点】切线的性质;三角形的外角性质;圆周角定理.
【分析】连接BD,有题意可知当P和D重合时,∠APB的度数最大,利用圆周角定理和直角三角形的性质即可求出∠ABP的度数.
【解答】解:连接BD,∵直线CD与以线段AB为直径的圆相切于点D,∴∠ADB=90°,
当∠APB的度数最大时,则P和D重合,∴∠APB=90°,
∵AB=2,AD=1,∴sin∠DBP=AD/AB =1/2 ,∴∠ABP=30°,
∴当∠APB的度数最大时,∠ABP的度数为30°.故选B.
【点评】本题考查了切线的性质,圆周角定理以及解直角三角形的有关知识,解题的关键是有题意可知当P和D重合时,∠APB的度数最大为90°.(圆内角>圆周角>圆外角)
5、【解析】解:连接OC,如图所示:
∵圆心角∠BOC与圆周角∠CBD都对,∴∠BOC=2∠CBD,又∠CDB=20°,
∴∠BOC=40°,又∵CE为圆O的切线,∴OC⊥CE,即∠OCE=90°,
则∠E=90°﹣40°=50°.故选B
【点评】本题主要考查了圆的切线的性质、同圆中同弧所对的圆周角相等及等边对等角等性质;解决本题的关键是熟悉圆中常见辅助线作法及相关性质.难度中等.
6、
考点:
切线的性质。
分析:
由BC与⊙0相切于点B,根据切线的性质,即可求得∠OBC=90°,又由∠ABC=70°,即可求得∠OBA的度数,然后由OA=OB,利用等边对等角的知识,即可求得∠A的度数.
解答:
解:∵BC与⊙0相切于点B,∴OB⊥BC,∴∠OBC=90°,
∵∠ABC=70°,∴∠OBA=∠OBC﹣∠ABC=90°﹣70°=20°,
∵OA=OB,∴∠A=∠OBA=20°.故选B.
点评:
此题考查了切线的性质与等腰三角形的性质.此题比较简单,注意数形结合思想的应用,注意圆的切线垂直于经过切点的半径定理的应用.
7、
考点:
切线的性质;角平分线的性质;勾股定理;相似三角形的判定与性质。
专题:
计算题。
分析:
(1)连接OC,根据切线的性质判断出AD∥OC,得到∠DAC=∠OCA,再根据OA=OC得到∠OAC=∠OCA,
可得AC平分∠BAD.
(2)连接BC,得到△ADC∽△ACB,根据相似三角形的性质即可求出AB的长.
解答:
解:(1)如图:连接OC,
∵DC切⊙O于C,∴AD⊥CD,∴∠ADC=∠OCF=90°,∴AD∥OC,
∴∠DAC=∠OCA,
∵OA=OC,∴∠OAC=∠OCA,即AC平分∠BAD.
(2)连接BC.
∵AB是直径,∴∠ACB=90°=∠ADC,
∵∠OAC=∠OCA,∴△ADC∽△ACB,∴,
在Rt△ADC中,AC=2,CD=2,∴AD=4,∴,∴AB=5.
8、解析:(1)过AB的中点O作OE⊥CD于E.证明OE的长等于半径即可.(2)证明∠COD=900,运用勾股定理求值..
答案:证明: 过AB的中点O作OE⊥CD于E.
S梯形ABCD=(AD+BC) ?AB=(AD+BC) ?OA=2(AD?OA+BC?OB)
=2(S⊿OAD +S⊿OBC)
由S梯形ABCD =S⊿OBC+ S⊿OAD+ S⊿OCD∴S⊿OBC+ S⊿OAD=S⊿OCD
∴AD?OA+BC?OA=CD·OE
∴(AD+BC) ·OA=CD·OE又AD+BC=CD
∴OA=OE,∴E点在以AB为直径的⊙O上,又OE⊥CD∴CD是⊙O的切线
即:CD与⊙O相切 …………5分
(2)∵DA、DE均为⊙O的切线,∴DA=DE,则∠1=∠2,同理∠3=∠4. ∴∠COD=900.
∴CD= …………5分
点评:本题考查梯形、直线余与圆的位置关系、勾股定理.根据圆的切线的定义准确的作出辅助线是解决问题的关键.本题中运用面积法证明AD+BC=CD很巧妙.难度较大.
9、解析:(1)欲证明BF是⊙O的切线,只需证明AB⊥BF即可;
(2)连接BD,在直角三角形ABD中,利用摄影定理可以求得AE的长度,最后结合图形知BE=AB﹣AE;
(3)连接BC.四边形CBFD为平行四边形,则四边形ACBD是正方形.根据平行四边形的对边平行、平行线的性质、圆周角定理以及同弧所对的圆周角相等可以推知∠CAD=∠BDA=90°,即CD是⊙O的直径,然后由全等三角形的判定与性质推知AC=BD;根据正方形的判定定理证得四边形ACBD是正方形.
答案:解:(1)∵AB是⊙O的直径,CD⊥AB,BF∥CD,
∴BF⊥AB,即BF是⊙O的切线;
(2)如图1,连接BD.∵AB是⊙O的直径,∴∠ADB=90°(直径所对的圆周角是直角);
又∵DE⊥AB∴AD2=AE?AB;
∵AD=8cm,AB=10cm,AE=6.4cm,∴BE=AB﹣AE=3.6cm;
(3)连接BC.
四边形CBFD为平行四边形,则四边形ACBD是正方形.理由如下:
∵四边形CBFD为平行四边形,∴BC∥FD,即BC∥AD;
∴∠BCD=∠ADC(两直线平行,内错角相等),
∵∠BCD=∠BAD,∠CAB=∠CDB,(同弧所对的圆周角相等),
∴∠CAB+∠BAD=∠CDB+∠ADC,即∠CAD=∠BDA;
又∵∠BDA=90°(直径所对的圆周角是直角),∴∠CAD=∠BDA=90°,
∴CD是⊙O的直径,即点E与点O重合(或线段CD过圆形O),如图2,
在△OBC和△ODA中,
∵,∴△OBC≌△ODA(SAS),
∴BC=DA(全等三角形的对应边相等),
∴四边形ACBD是平行四边形(对边平行且相等的四边形是平行四边形);
∵∠ACB=90°(直径所对的圆周角是直角),AC=AD,∴四边形ACBD是正方形.
10、
考点:
切线的判定与性质;一次函数综合题;全等三角形的判定与性质;勾股定理;矩形的性质;相似三角形的判定与性质。
专题:
计算题;证明题。
解答:
(1)①解:E的坐标是:(1,),
②证明:∵矩形OABC,∴CE=AE,BC∥OA,∴∠HCE=∠EAG,
∵在△CHE和△AGE中,∴△CHE≌△AGE,∴AG=CH.
(2)解:连接DE并延长DE交CB于M,
∵DD=OC=1=OA,∴D是OA的中点,
∵在△CME和△ADE中,∴△CME≌△ADE,
∴CM=AD=2-1=1,
∵BC∥OA,∠COD=90°,∴四边形CMDO是矩形,∴MD⊥OD,MD⊥CB,
∴MD切⊙O于D,
∵得HG切⊙O于F,E(1,),∴可设CH=HF=x,FE=ED==ME,
在Rt△MHE中,有MH2+ME2=HE2
即(1-x)2+()2=(+x)2,解得x=,∴H(,1),OG=2-=,
又∵G(,0),设直线GH的解析式是:y=kx+b,
把G、H的坐标代入得:0=b,且1=k+b,得:k=-,b=,
∴直线GH的函数关系式为y=-.
(3)解:连接BG,
∵在△OCH和△BAG中,∴△OCH≌△BAG,
∴∠CHO=∠AGB,
∵∠HCO=90°,∴HC切⊙O于C,HG切⊙O于F,∴OH平分∠CHF,
∴∠CHO=∠FHO=∠BGA,
∵△CHE≌△AGE,∴HE=GE,
在△HOE和△GBE中,∴△HOE≌△GBE,
∴∠OHE=∠BGE,21世纪教育网
∵∠CHO=∠FHO=∠BGA,∴∠BGA=∠BGE,即BG平分∠FGA,
∵⊙P与HG、GA、AB都相切,∴圆心P必在BG上,
过P做PN⊥GA,垂足为N,∴△GPN∽△GBA,∴,
设半径为r,=,解得:r=,答:⊙P的半径是.
点评:
本题综合考查了矩形的性质和判定,全等三角形的性质和判定,相似三角形的性质和判定,切线的性质和判定,一次函数和勾股定理等知识点,本题综合性比较强,难度偏大,但是也是一道比较好的题目.
辅导:圆的切线
(一)学习要求:
【学习目标】
1.了解切线的概念,探索切线与过切点的半径之间的关系.
2.能判定一条直线是否为圆的切线,理解切线的判定定理、性质定理.
3.会过圆上点画圆的切线.
【学习重点】切线判定定理、性质定理的区别与应用.
(二)知识要点:
1. 直线是圆的切线.
2.直线与⊙O相切于点A,OA是过切点的半径,直线与半径OA位置关系如何?
圆的切线 经过 的半径.
(三)例题展现:
问题1:(2012?衢州第21题)如图,在Rt△ABC中,∠C=90°,∠ABC的平分线交AC于点D,点O是AB上一点,⊙O过B、D两点,且分别交AB、BC于点E、F.
(1)求证:AC是⊙O的切线;
(2)已知AB=10,BC=6,求⊙O的半径r.
问题2:(2012?丽水第20题)如图,AB为⊙O的直径,EF切⊙O于点D,过点B作BH⊥EF于点H,交⊙O于点C,连接BD.
(1)求证:BD平分∠ABH;
(2)如果AB=12,BC=8,求圆心O到BC的距离.
(四)自我体会:
1、(2012山东省荷泽市,11,3)如图,PA、PB是⊙o的切线,A、B为切点,AC是⊙o 的直径,若∠P=46°,则∠BAC=______.
2、(2012?扬州)如图,PA、PB是⊙O的切线,切点分别为A、B两点,点C在⊙O上,如果ACB=70°,那么∠P的度数是 .
3、(2012海南)如图,∠APB=300,圆心在边PB上的⊙O半径为1cm,OP=3cm,若⊙O沿BP方向移动,当⊙O与直线PA相切时,圆心O移动的距离为 cm.
4、(2012?黄石)如图(4)所示,直线与线段为直径的圆相切于点,并交的延长线于点,且,,点在切线上移动.当的度数最大时,则的度数为( )
A. ° B. ° C. ° D. °
5、(2012山西,9,2分)如图,AB是⊙O的直径,C.D是⊙O上一点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于( )
A. 40° B. 50° C.60° D.70°
6、(2012?嘉兴第4题)如图,AB是⊙0的弦,BC与⊙0相切于点B,连接OA、OB.若∠ABC=70°,则∠A等于( )
A.15° B.20° C.30° D.70°
7、(2012?扬州)如图,AB是⊙O的直径,C是⊙O上一点,AD垂直于过点C的切线,垂足为D.(1)求证:AC平分BAD;(2)若AC=2,CD=2,求⊙O的直径.
8、(2012湖北随州,23,10分) 如图,已知直角梯形ABCD,∠B=90°,AD∥BC,并且AD+BC=CD,O为AB的中点.
(1)求证:以AB为直径的⊙O与斜腰CD相切;
(2)若OC=8cm,OD=6cm,求CD的长.
9、(2012湖南衡阳市,26,8)如图,AB是⊙O的直径,动弦CD垂直AB于点E,过点B作直线BF∥CD交AD的延长线于点F,若AB=10cm.
(1)求证:BF是⊙O的切线.
(2)若AD=8cm,求BE的长.
(3)若四边形CBFD为平行四边形,则四边形ACBD为何种四边形?并说明理由.
10、(2012?扬州)如图1,在平面直角坐标系中,矩形OABC的顶点O在坐标原点,顶点A、C分别在x轴、y轴的正半轴上,且OA=2,OC=1,矩形对角线AC、OB相交于E,过点E的直线与边OA、BC分别相交于点G、H.
(1)①直接写出点E的坐标: .
②求证:AG=CH.
(2)如图2,以O为圆心,OC为半径的圆弧交OA与D,若直线GH与弧CD所在的圆相切于矩形内一点F,求直线GH的函数关系式.
(3)在(2)的结论下,梯形ABHG的内部有一点P,当⊙P与HG、GA、AB都相切时,求⊙P的半径.
问题1:
考点:
切线的判定;相似三角形的判定与性质。
分析:
(1)连接OD.欲证AC是⊙O的切线,只需证明AC⊥OD即可;
(2)利用平行线截线段成比例推知=;然后将图中线段间的和差关系代入该比例式,通过解方程即可求得r的值,即⊙O的半径r的值.
解答:
(1)证明:连接OD.
∵OB=OD,∴∠OBD=∠ODB(等角对等边);
∵BD平分∠ABC,∴∠ABD=∠DBC,∴∠ODB=∠DBC(等量代换),
∴OD∥BC(内错角相等,两直线平行);
又∵∠C=90°(已知),∴∠ADO=90°(两直线平行,同位角相等),
∴AC⊥OD,即AC是⊙O的切线;
(2)解:由(1)知,OD∥BC,∴=(平行线截线段成比例),
∴=,解得r=,即⊙O的半径r为.
点评:
本题综合考查了切线的判定、平行线截线段成比例等知识点.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.
问题2:
考点:
切线的性质;勾股定理;垂径定理;圆周角定理。
分析:
(1)连接OD,根据切线的性质以及BH⊥EF,即可证得OD∥BC,然后根据等边对等角即可证得;
(2)过点O作OG⊥BC于点G,则利用垂径定理即可求得BG的长,然后在直角△OBG中利用勾股定理即可求解.
解答:
(1)证明:连接OD,
∵EF是⊙O的切线,∴OD⊥EF,
又∵BH⊥EF,∴OD∥BH,∴∠ODB=∠DBH,
∵OD=OB,∴∠ODB=∠OBD∴∠OBD=∠DBH,∴BD平分∠ABH.
(2)解:过点O作OG⊥BC于点G,则BG=CG=4,
在Rt△OBG中,OG===.
点评:
本题考查了切线的性质定理,以及勾股定理,注意到OD∥BC是关键.
(四)自我体会:
1、【解析】因为PA、PB是⊙o的切线,所以PA=PB,OA⊥PA,又因∠P=46°,所以∠PAB=67°,所以∠BAC=∠OAP-∠PAB=90°-67°=23°,
【答案】23°
【点评】当圆外一点向圆引两条切线,可以利用切线长定理及切线的性质定理,利用等腰三角形的性质及及垂直的性质来计算角的度数.
2、
考点:
切线的性质;多边形内角与外角;圆周角定理。
专题:
计算题。
分析:
连接OA,OB,由PA与PB都为圆O的切线,利用切线的性质得到OA垂直于AP,OB垂直于BP,可得出两个角为直角,再由同弧所对的圆心角等于所对圆周角的2倍,由已知∠ACB的度数求出∠AOB的度数,在四边形PABO中,根据四边形的内角和定理即可求出∠P的度数.
解答:
解:连接OA,OB,如图所示:
∵PA、PB是⊙O的切线,∴OA⊥AP,OB⊥BP,∴∠OAP=∠OBP=90°,
又∵圆心角∠AOB与圆周角∠ACB都对,且∠ACB=70°,
∴∠AOB=2∠ACB=140°,则∠P=360°-(90°+90°+140°)=40°.故答案为:40°
点评:
此题考查了切线的性质,四边形的内角与外角,以及圆周角定理,连接OA与OB,熟练运用性质及定理是解本题的关键.
3、【答案】1或5。
【考点】直线与圆相切的性质,含300角直角三角形的性质。
【分析】如图,设⊙O移动到⊙O1,⊙O2位置时与PA相切。
当⊙O移动到⊙O1时,∠O1DP=900。
∵∠APB=300,O1D=1,∴PO1=2。∵OP=3,∴OO1=1。
当⊙O移动到⊙O2时,∠O2EP=900。
∵∠APB=300,O2D=1,∴∠O2PE=300,PO2=2。
∵OP=3,∴OO1=5。
综上所述,当⊙O与PA相切时,圆心O移动的距离为1cm或5 cm。
4、【考点】切线的性质;三角形的外角性质;圆周角定理.
【分析】连接BD,有题意可知当P和D重合时,∠APB的度数最大,利用圆周角定理和直角三角形的性质即可求出∠ABP的度数.
【解答】解:连接BD,∵直线CD与以线段AB为直径的圆相切于点D,∴∠ADB=90°,
当∠APB的度数最大时,则P和D重合,∴∠APB=90°,
∵AB=2,AD=1,∴sin∠DBP=AD/AB =1/2 ,∴∠ABP=30°,
∴当∠APB的度数最大时,∠ABP的度数为30°.故选B.
【点评】本题考查了切线的性质,圆周角定理以及解直角三角形的有关知识,解题的关键是有题意可知当P和D重合时,∠APB的度数最大为90°.(圆内角>圆周角>圆外角)
5、【解析】解:连接OC,如图所示:
∵圆心角∠BOC与圆周角∠CBD都对,∴∠BOC=2∠CBD,又∠CDB=20°,
∴∠BOC=40°,又∵CE为圆O的切线,∴OC⊥CE,即∠OCE=90°,
则∠E=90°﹣40°=50°.故选B
【点评】本题主要考查了圆的切线的性质、同圆中同弧所对的圆周角相等及等边对等角等性质;解决本题的关键是熟悉圆中常见辅助线作法及相关性质.难度中等.
6、
考点:
切线的性质。
分析:
由BC与⊙0相切于点B,根据切线的性质,即可求得∠OBC=90°,又由∠ABC=70°,即可求得∠OBA的度数,然后由OA=OB,利用等边对等角的知识,即可求得∠A的度数.
解答:
解:∵BC与⊙0相切于点B,∴OB⊥BC,∴∠OBC=90°,
∵∠ABC=70°,∴∠OBA=∠OBC﹣∠ABC=90°﹣70°=20°,
∵OA=OB,∴∠A=∠OBA=20°.故选B.
点评:
此题考查了切线的性质与等腰三角形的性质.此题比较简单,注意数形结合思想的应用,注意圆的切线垂直于经过切点的半径定理的应用.
7、
考点:
切线的性质;角平分线的性质;勾股定理;相似三角形的判定与性质。
专题:
计算题。
分析:
(1)连接OC,根据切线的性质判断出AD∥OC,得到∠DAC=∠OCA,再根据OA=OC得到∠OAC=∠OCA,
可得AC平分∠BAD.
(2)连接BC,得到△ADC∽△ACB,根据相似三角形的性质即可求出AB的长.
解答:
解:(1)如图:连接OC,
∵DC切⊙O于C,∴AD⊥CD,∴∠ADC=∠OCF=90°,∴AD∥OC,
∴∠DAC=∠OCA,
∵OA=OC,∴∠OAC=∠OCA,即AC平分∠BAD.
(2)连接BC.
∵AB是直径,∴∠ACB=90°=∠ADC,
∵∠OAC=∠OCA,∴△ADC∽△ACB,∴,
在Rt△ADC中,AC=2,CD=2,∴AD=4,∴,∴AB=5.
8、解析:(1)过AB的中点O作OE⊥CD于E.证明OE的长等于半径即可.(2)证明∠COD=900,运用勾股定理求值..
答案:证明: 过AB的中点O作OE⊥CD于E.
S梯形ABCD=(AD+BC) ?AB=(AD+BC) ?OA=2(AD?OA+BC?OB)
=2(S⊿OAD +S⊿OBC)
由S梯形ABCD =S⊿OBC+ S⊿OAD+ S⊿OCD∴S⊿OBC+ S⊿OAD=S⊿OCD
∴AD?OA+BC?OA=CD·OE
∴(AD+BC) ·OA=CD·OE又AD+BC=CD
∴OA=OE,∴E点在以AB为直径的⊙O上,又OE⊥CD∴CD是⊙O的切线
即:CD与⊙O相切 …………5分
(2)∵DA、DE均为⊙O的切线,∴DA=DE,则∠1=∠2,同理∠3=∠4. ∴∠COD=900.
∴CD= …………5分
点评:本题考查梯形、直线余与圆的位置关系、勾股定理.根据圆的切线的定义准确的作出辅助线是解决问题的关键.本题中运用面积法证明AD+BC=CD很巧妙.难度较大.
9、解析:(1)欲证明BF是⊙O的切线,只需证明AB⊥BF即可;
(2)连接BD,在直角三角形ABD中,利用摄影定理可以求得AE的长度,最后结合图形知BE=AB﹣AE;
(3)连接BC.四边形CBFD为平行四边形,则四边形ACBD是正方形.根据平行四边形的对边平行、平行线的性质、圆周角定理以及同弧所对的圆周角相等可以推知∠CAD=∠BDA=90°,即CD是⊙O的直径,然后由全等三角形的判定与性质推知AC=BD;根据正方形的判定定理证得四边形ACBD是正方形.
答案:解:(1)∵AB是⊙O的直径,CD⊥AB,BF∥CD,
∴BF⊥AB,即BF是⊙O的切线;
(2)如图1,连接BD.∵AB是⊙O的直径,∴∠ADB=90°(直径所对的圆周角是直角);
又∵DE⊥AB∴AD2=AE?AB;
∵AD=8cm,AB=10cm,AE=6.4cm,∴BE=AB﹣AE=3.6cm;
(3)连接BC.
四边形CBFD为平行四边形,则四边形ACBD是正方形.理由如下:
∵四边形CBFD为平行四边形,∴BC∥FD,即BC∥AD;
∴∠BCD=∠ADC(两直线平行,内错角相等),
∵∠BCD=∠BAD,∠CAB=∠CDB,(同弧所对的圆周角相等),
∴∠CAB+∠BAD=∠CDB+∠ADC,即∠CAD=∠BDA;
又∵∠BDA=90°(直径所对的圆周角是直角),∴∠CAD=∠BDA=90°,
∴CD是⊙O的直径,即点E与点O重合(或线段CD过圆形O),如图2,
在△OBC和△ODA中,
∵,∴△OBC≌△ODA(SAS),
∴BC=DA(全等三角形的对应边相等),
∴四边形ACBD是平行四边形(对边平行且相等的四边形是平行四边形);
∵∠ACB=90°(直径所对的圆周角是直角),AC=AD,∴四边形ACBD是正方形.
10、
考点:
切线的判定与性质;一次函数综合题;全等三角形的判定与性质;勾股定理;矩形的性质;相似三角形的判定与性质。
专题:
计算题;证明题。
解答:
(1)①解:E的坐标是:(1,),
②证明:∵矩形OABC,∴CE=AE,BC∥OA,∴∠HCE=∠EAG,
∵在△CHE和△AGE中,∴△CHE≌△AGE,∴AG=CH.
(2)解:连接DE并延长DE交CB于M,
∵DD=OC=1=OA,∴D是OA的中点,
∵在△CME和△ADE中,∴△CME≌△ADE,
∴CM=AD=2-1=1,
∵BC∥OA,∠COD=90°,∴四边形CMDO是矩形,∴MD⊥OD,MD⊥CB,
∴MD切⊙O于D,
∵得HG切⊙O于F,E(1,),∴可设CH=HF=x,FE=ED==ME,
在Rt△MHE中,有MH2+ME2=HE2
即(1-x)2+()2=(+x)2,解得x=,∴H(,1),OG=2-=,
又∵G(,0),设直线GH的解析式是:y=kx+b,
把G、H的坐标代入得:0=b,且1=k+b,得:k=-,b=,
∴直线GH的函数关系式为y=-.
(3)解:连接BG,
∵在△OCH和△BAG中,∴△OCH≌△BAG,
∴∠CHO=∠AGB,
∵∠HCO=90°,∴HC切⊙O于C,HG切⊙O于F,∴OH平分∠CHF,
∴∠CHO=∠FHO=∠BGA,
∵△CHE≌△AGE,∴HE=GE,
在△HOE和△GBE中,∴△HOE≌△GBE,
∴∠OHE=∠BGE,21世纪教育网
∵∠CHO=∠FHO=∠BGA,∴∠BGA=∠BGE,即BG平分∠FGA,
∵⊙P与HG、GA、AB都相切,∴圆心P必在BG上,
过P做PN⊥GA,垂足为N,∴△GPN∽△GBA,∴,
设半径为r,=,解得:r=,答:⊙P的半径是.
点评:
本题综合考查了矩形的性质和判定,全等三角形的性质和判定,相似三角形的性质和判定,切线的性质和判定,一次函数和勾股定理等知识点,本题综合性比较强,难度偏大,但是也是一道比较好的题目.
同课章节目录
